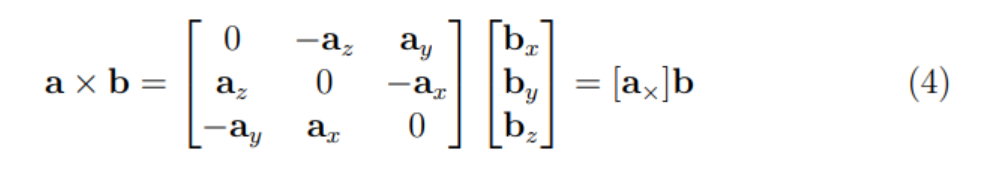3. Affine structure from motion

structure from motion(SfM)은 multiple view 이미지로부터 씬(scene)의 3D 구조와 카메라 파라미터를 동시에 결정할 수 있는 방법이다.

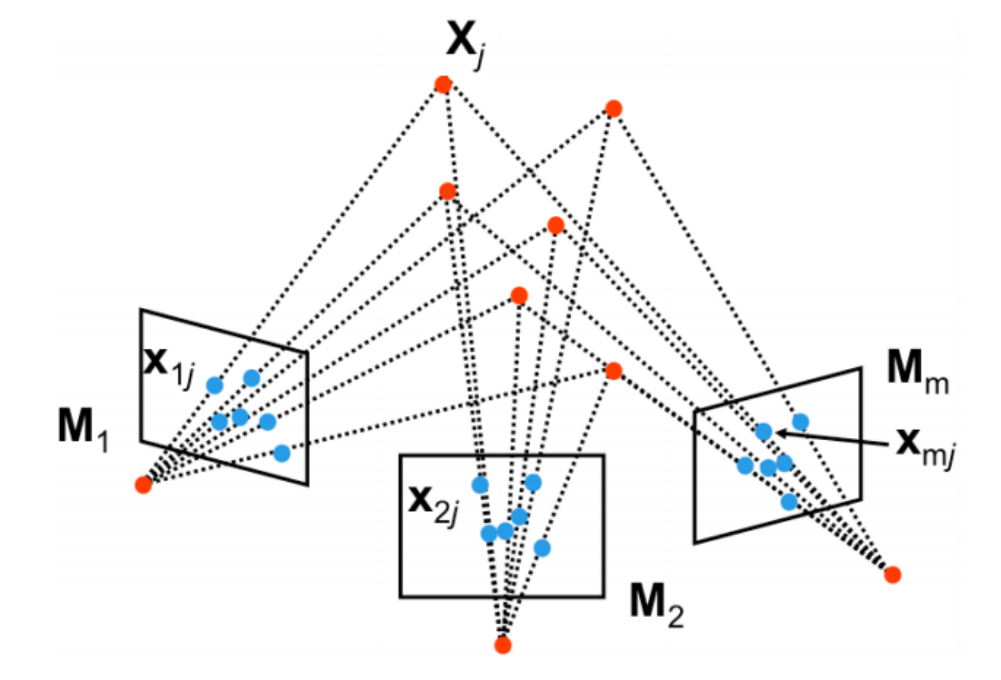
• $M_i$ : i번째 카메라의 intrinsic and extrinsic 파라미터
• $X_j$ : 씬에 있는 n개의 포인트 중 j번째 포인트
• $x_{ij}$ : $X_j$가 i번째 카메라의 이미지 평면에 투영된 점 ($x_{ij} = M_iX_j$)

3.1 Affine structure from motion problem

먼저 좀 더 단순한 문제를 풀기 위해 모든 카메라가 weak perspective, 즉 원근감을 거의 표현하지 않는 카메라라고 가정하자.

이 경우 3D에서 2D로의 변환은 depth에 따른 scale 변환이 없는 affine transform이 된다.

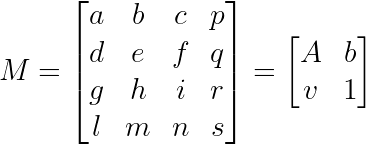
perspective camera의 변환 행렬을 다음과 같이 나타낼 수 있는데, weak perspective의 경우 x, y, z축 방향 depth에 따른 scale 변환이 없으므로 $v=0$이 된다.

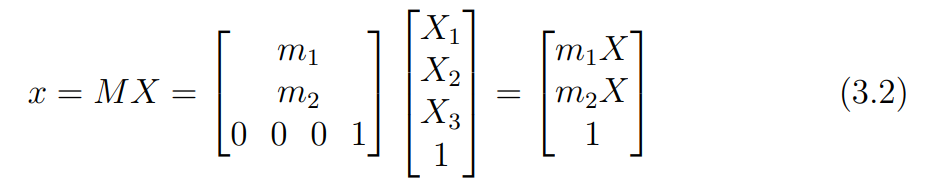
$v=0$일 경우 $M$의 마지막 행이 $[0, 0, 0, 1]$이므로, homogeneous 좌표에서 scale을 나타내는 마지막 행이 1이된다.

즉, weak perspective camera 모델에서 $M$에 의한 변환은 선형적이라는 것을 알 수 있다.

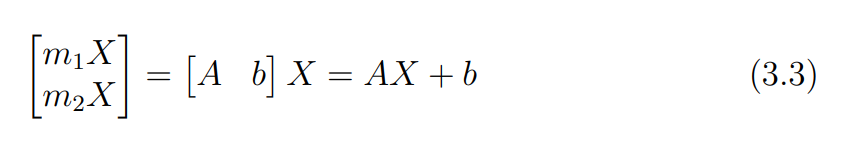
때문에 변환식을 위와 같이 선형 변환식(식 3.3)으로 나타낼 수 있다.

문제 정의

SfM 문제에서 우리가 알고자 하는 것은 카메라의 파라미터 $M_i$와 3D의 월드 좌표 $X_j$이다.

$M_i$는 아핀 변환이므로 3 + 3 + 2 = 8개의 변수를 갖는는다. (각각 scale, rotation, translation)

$X_j$는 3차원 좌표이므로 3개의 변수를 갖는다.

즉 m개의 카메라, n개의 관측점이 있을 때 $2mn$개의 방정식과 $8m + 3n$개의 변수가 존재하므로, $2mn > 8m + 3n$의 조건을 만족해야 $M, X$를 구하는 문제를 풀 수 있다.

예를들어 카메라가 2개라면($m=2$), 적어도 16개의 관측점($n=16$)이 필요하다.

3.2 The Tomasi and Kanade factorization method

이렇게 정의된 Affine SfM을 풀기 위해 Tomasi and Kanade factorization method를 풀 수 있다.

이 방법은 크게 data centering step, actual factorization step 두 단계로 구성된다.

data centering step

data centering step은 이미지의 중앙점이 원점(0, 0)이 되도록 하는 과정이다.

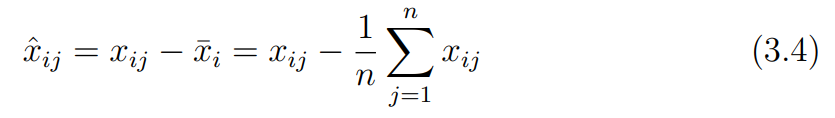
모든 관측점 좌표의 평균을 중앙점 $\bar{x}_i$으로 하여, 중앙점을 기준으로 cetering된 새로운 좌표 $\hat{x}_{ij}$를 구한다.

$x_{ij} = A_iX_j + b_i$이므로 centering 된 좌표를 통해 다음의 식을 유도할 수 있다.

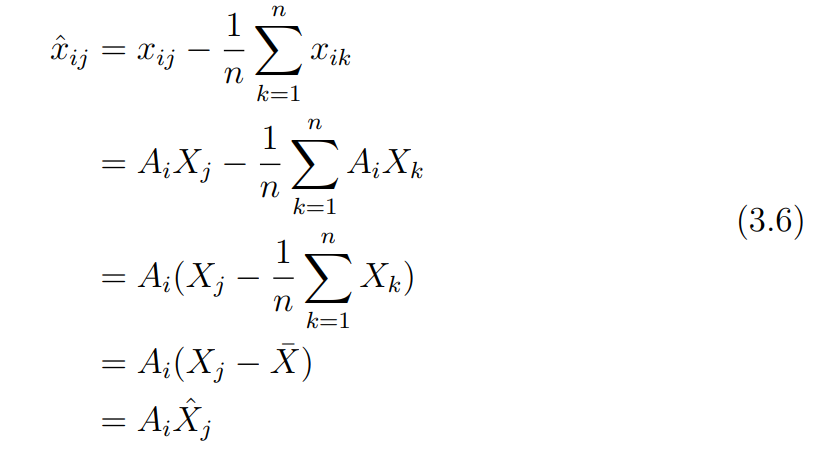
centering 과정에서 모든 관측점에 대해 평균을 뺴주었기 때문에 bias를 제거할 수 있다.

즉 $\hat{x}_{ij}$는 마찬가지로 센터링 된 $\hat{X}_j$에 대해 affine 변환행렬만을 적용한 결과가 된다. 이걸로 문제가 조금 더 단순화 된다.

actual factorization step

이제 우리가 알고 있는 $\hat{x}_{ij}$를 바탕으로 $A_i, X_j$를 예측해야 한다.

먼저 모든 m개 카메라, n개의 포인트를 합쳐 하나의 관측 행렬 $D$를 정의해보자.

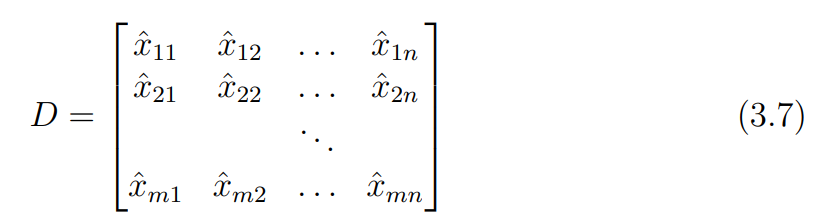
모든 관측치를 하나로 만들어 줬으므로, 모든 변환 행렬을 합친 2m x 3 motion matrix($M$), 모든 관측점을 합친 3 x n structure matrix($S$)의 곱으로 나타낼 수 있다.

• $D = MS$

여기서 중요한 것은 $rank(D) = 3$이라는 것이다.
$S$는 3차원 포인트들로 구성된 행렬이기에 최대 rank가 3이며, $M$은 아핀변환을 수행하는 행렬이기 때문에 마찬가지로 최대 rank가 3이기 때문이다.

즉, $D$를 SVD를 통해 $D = U\Sigma V^T$로 분해했을 때, $\Sigma$는 주대각선에 3개의 0이 아닌 특이값을 갖는 대각 행렬이 된다.

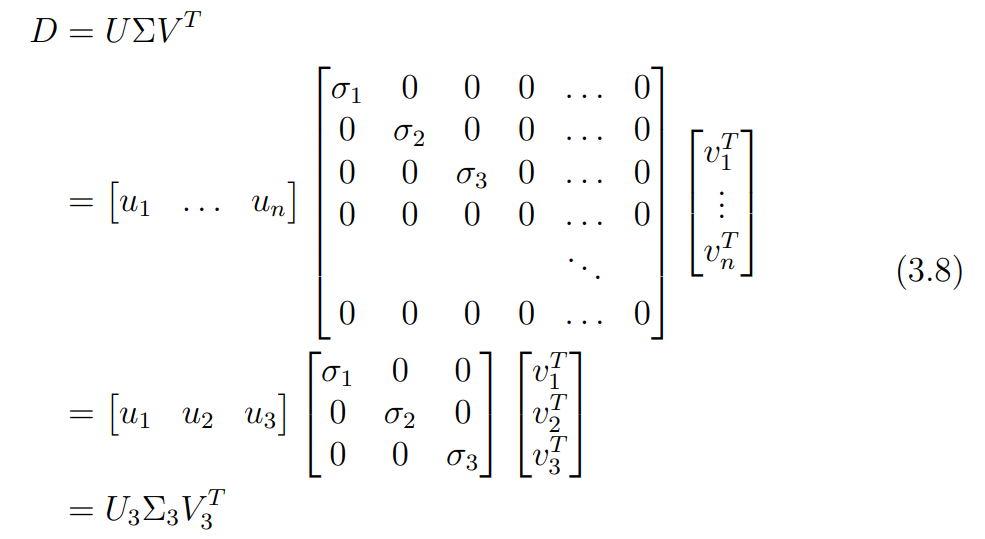
이를 이용해 SVD를 식 3.8과 같이 단순화하여 나타낼 수 있다.

실제로는 노이즈, 카메라 캘리브레이션 오차 등으로 인해 $D$의 rank가 3보다 커질 수 있지만, 그래도 가능한 최적의 접근법이다.

식 3.8은 2m x n 행렬을 SVD한 결과이므로, $U_3$ 가 2m x 3 크기의 행렬이며, $\Sigma_3V_3^T$ 가 3 x n 행렬이라는 것을 알 수 있다.
이는 앞서 정의했던 S, M과 동일한 size이다.

즉 식 3.8을 factorization하여 $M, S$를 정의함으로써 $D$에 대한 SfM문제를 풀 수 있다.

예를 들어 $M = U_3\Sigma_3$, $S = V^T_3$으로 정의할 수 있다.
이 경우, $U_3\Sigma_3$가 카메라 파라미터를, $V^T_3$가 3D 구조를 나타낸다고 가정한 것이다.

여기서 특이값 행렬인 $\Sigma$를 어느 항에 붙일지로 다양한 해석이 가능한데, Tomasi and Kanade는 특이값을 균등하게 분배하여 $S, M$이 각각 기하학적 구조를 효과적으로 반영할 수 있도록 $M = U_3\sqrt{\Sigma_3}$, $S = \sqrt{\Sigma_3}V^T_3$으로 factorization 하였다.

3.3 Ambiguity in reconstruction

$D = MS$를 factorization하는 방법에는 내재된 모호성(ambiguity)가 존재한다.

바로 역행렬이 존재하는 임의의 3 x 3 행렬 $A$를 식에 삽입할 수 있기 때문이다.

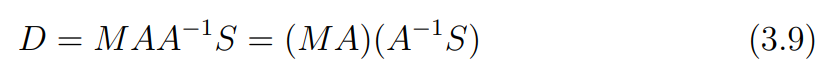
이 경우 $MA = U_3\Sigma_3$, $A^{-1}S = V^T_3$와 같이 동일한 $D$에 대해 $M, S$가 여러개 존재할 수 있기 때문에, $M, S$로 재구성된 3D 모델이 현실과 일치하지 않을 수도 있다.

이 $A$는 affine 변환에 대한 모호성을 나타내기 때문에, 3D 모델에서의 점들의 평행성과 같은 관계는 유지되며, metric scale은 알 수 없다.

만약 카메라가 intrinsic callibration 되었다면, 실제 현실에서 translation, rotation, scale만 다른 similarity(유사 변환에 대한) 모호성만 갖는 $M, S$를 구할 수 있다.

여기에 부족한 정보를 보충하는 추가 정보가 있다면 이러한 모호성을 해결할 수도 있다. 예를 들어 카메라를 고정하고, 물체만 점점 멀어지게하여 상대적인 scale을 구할 수 있는 경우가 있다.

3.4 정리

정리하자면 weak perspective model에서 $2mn > 8m + 3n$을 만족하는 m개의 카메라, n개의 관측점이 있다면 SfM을 이용해 카메라 파라미터 $M$과 물체에 대한 3D 월드좌표 $S$를 구할 수 있다는 것이다.

다만, 여기에는 아핀 변환에 대한 모호성이 있기 때문에 이미지로 부터 재구성 된 모델이 현실과 일치하지 않을 수 있다. 이 재구성된 모델은 현실에서 affine 변환 또는 유사 변환된 형태이므로, point 간의 관계를 현실과 일치하며, 추가적인 정보가 주어진다면 모호성을 해결할 수도 있다.

4. Perspective structure from motion

이제 좀 더 일반적인 케이스인 perspective camera에 대한 SfM을 알아보자.

perspective camera의 변환 행렬은 자유도 11인 투영변환 행렬이다.

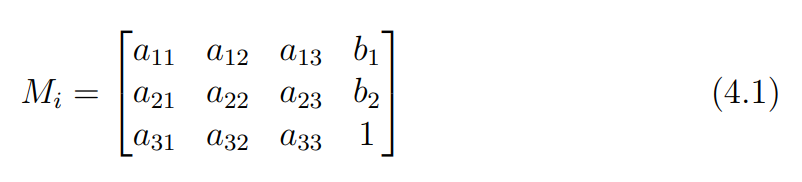
앞서 weak perspective model에서는 $\hat{x}_{ij} = A_iX_j$로 3 x 3 아핀 변환 행렬 $A$를 사용했지만, perspective camera에서는 $A$ 대신 4 x 4의 투영 변환 행렬 $H$를 사용해 SfM 문제를 푼다.

앞서 weak perspective model과 유사하게 m개의 카메라, n개의 관측점에 대해 $2mn > 11m + 3n - 15$의 조건을 만족해야 SfM 문제를 풀 수 있다.
여기서 15를 빼는 이유는 $2mn$개의 관측점은 모두 투영 변환된 결과이기 때문이다. 모든 관측점에 대해 글로벌하게 적용되기 때문에 투영 변환 행렬 $H$가 변해도 시스템 내부의 구성은 영향을 받지 않기 때문에 $H$의 자유도 15를 빼준다.

4.1 The algebraic approach

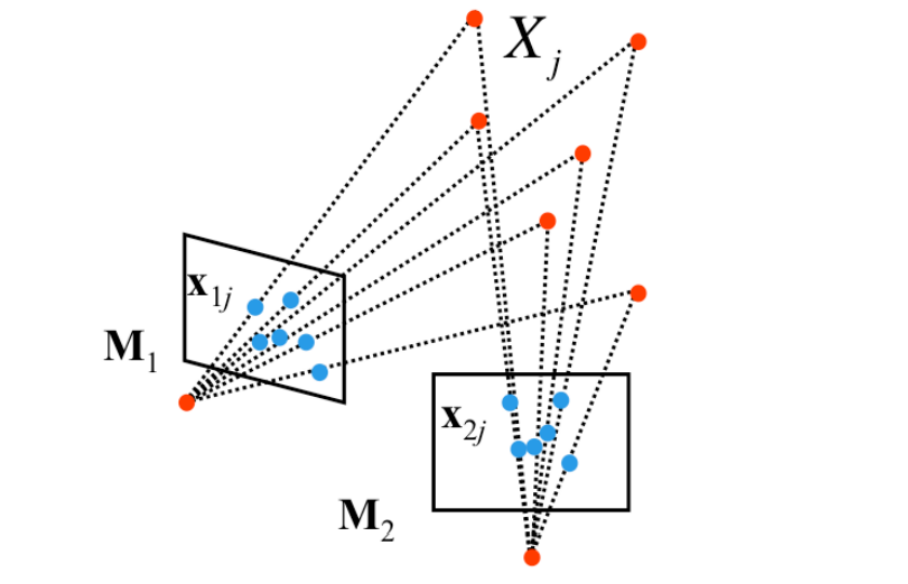
두 perspective 카메라에 대해 한 카메라를 canonical로 정의하면 문제를 조금 더 단순화 할 수 있다.

canonical 카메라는 카메라가 원점에 위치하며, view direction이 z축 방향으로 고정된 상태이기 때문에, 투영 변환 $H$가 적용되어도 좌표값이 변하지 않는다. ((x, y, z) → (x, y))

$M_1$이 canonical 카메라이고, 투영 변환 H가 적용된 것이라면 H의 역행렬을 이용해 아래 식 4.2와 같이 canonical로 만들 수 있다.

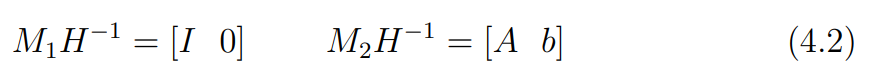
이렇게 하면 기준이 되는 canonical 카메라를 기준으로 다른 카메라를 상대적인 관계를 통해 나타낼 수 있다.

이렇게 3D point를 투영하는 변환 행렬을 정의하였으므로, 여기에 Fundametal Matrix $F$를 이용해 두 투영점의 관계를 알아냄으로써 두 카메라의 변환행렬 $M_1, M_2$를 예측할 수 있다.

먼저 기존 카메라 행렬에 $H^{-1}$을 적용하였으므로, 3D 구조에 H를 적용하여 원래 식과 일치하도록 만들어야 한다. (식 4.3)

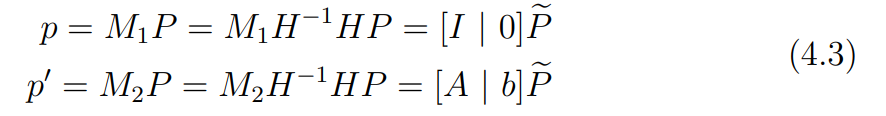
식 4.3의 $\tilde{P}$가 3D 구조에 $H$를 적용한 것이다.
그러면 $p, p'$를 아래와 같이 구할 수 있다.

$p = \tilde{P}$
$p' = A\tilde{P} + b = Ap + b$

여기서 $p'$와 $b$를 cross product하는 것을 통해 아래의 식 4.5를 유도할 수 있다.

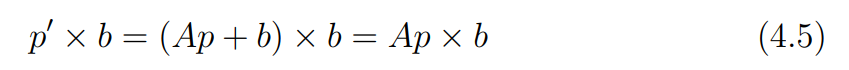
$Ap \times b$는 $p'$에 대해 수직이므로 dot product하면 0이 된다. 이를 이용해 아래의 식 4.6을 유도할 수 있다.

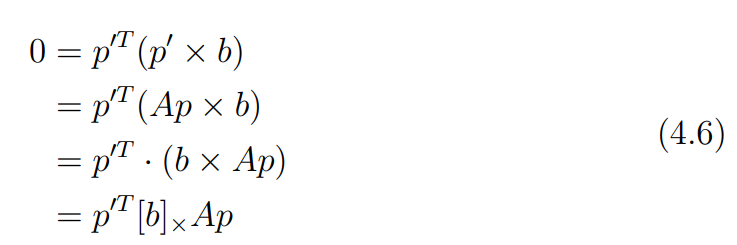
여기서 $[b]_\times$는 앞서 fundamental matrix를 구할 때 사용했던 cross product 행렬이다.

앞서 fundamental matrix를 정의했듯이 $F = [b]_\times A$가 되며 이는 두 점 $p, p'$ 사이의 기하학적 관계를 정의한다.

아래 문단은 주관적인 생각이 많이 포함되어있습니다.

fundametal matrix의 또 하나의 특징은 epipole과의 내적값이 0이라는 것이다.
여기서 $b$를 주목할 수 있는데, $Fb$를 계산하면 0임을 아래의 식 4.7을 통해 알 수 있다.

$b \times A$의 연산 결과는 $b$와 수직인 어떤 벡터이기 때문에 이를 다시 $b$와 내적하면 0이 된다.

즉 $F$와 $b$의 내적값이 0이라는 것은 $b$가 epipole이라는 것이다.

$F$는 역행렬이 없는 특이 행렬(singular)이기 떄문에 $Fb = 0$을 만족하는 영벡터가 아닌 $b$가 존재하며, 이를 SVD를 이용해 least square solution으로 풀 수 있다.

이렇게 $b$를 알아내었다면 $A$ 역시 구할 수 있다.
앞서 fundamental matrix를 $F=[b]_\times A$ 이라 정의했으므로, $A = -[b]_\times F$일 때, 이 조건을 만족할 수 있다. 아래 식 4.8을 통해 이를 보여준다.

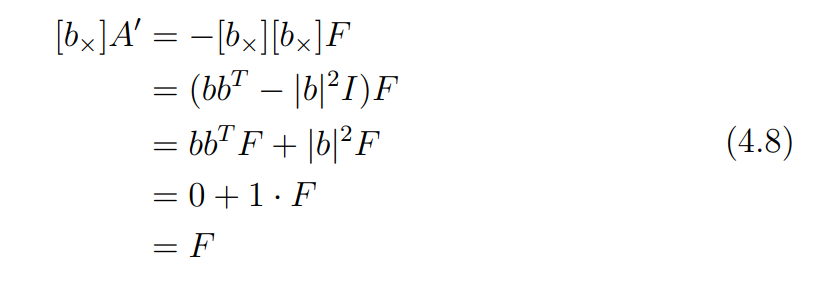
즉, $[A \:\: b]$를 아래 식 4.9와 같이 바꿔 나타낼 수 있다.

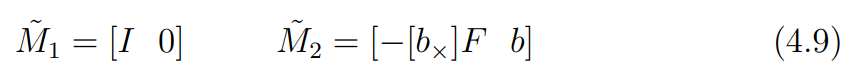
또한 앞서 $b$는 epipole을 나타낸다고 했으므로, 최종적으로 아래의 식 4.10을 얻을 수 있다.

이를 통해 기준 카메라의 epipole이 다른 카메라에 투영된 점 $e$를 알고 있을 때 $\tilde{M}_1, \tilde{M}_2$를 구할 수 있음을 나타낸다.

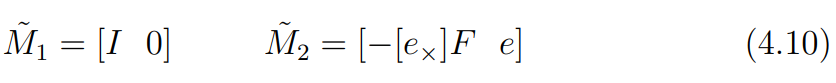
4.2 Determining motion from the Essential matrix

카메라의 intrinsic parameter 행렬 $K$를 알고 있다면 fundamental matrix $F$와 $K$를 이용해 essential matrix $E$를 구할 수 있다.

$F = K^{-T}EK^{-1}$
$E = K^TFK$

essential matrix는 회전 $R$과 3차원 이동 $t$ 정보를 담고 있는데, 바로 이 정보가 motion matrix를 구하는데 필요한 정보이다.

앞서 $D$를 분해하여 각각 motion, structure 정보를 담고 있는 $M, S$를 얻었듯이 $E$를 두 요소로 분해하여 $R, t$를 얻을 수 있다.

먼저 $E$를 분해하는 것에 사용할 두 행렬을 아래와 같이 정의한다.

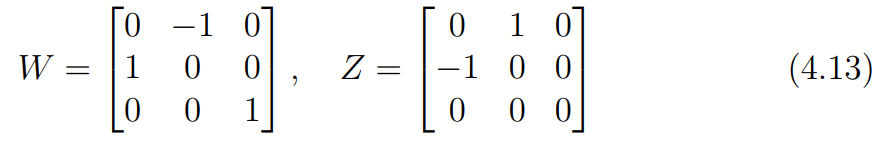
여기서 중요한 것은 부호를 고려하지 않았을 때(up to a sign) $Z = diag(1, 1, 0)W$를 만족한다는 것이다.
비슷하게 부호를 고려하지 않을 때 $ZW = ZW^T=diag(1, 1, 0)$를 만족한다.

식 4.12에서 $[t]_\times$를 eigenvalue decomposition하여 up to scale로 다음과 같이 나타낼 수 있다.

여기서 $U$는 essential matrix를 SVD하였을 때의 왼쪽 직교 행렬이다. ($E = U\Sigma V^T$)

즉 $E$를 아래의 식 4.15와 같이 나타낼 수 있다.

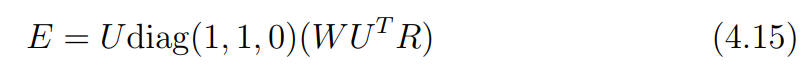
$E = U\Sigma V^T$에서 $\Sigma$는 두개의 non-zero sigular 값과 하나의 0값을 갖는 대각 행렬이라는 것을 생각하면, 식 4.15로 부터 아래의 식을 유도할 수 있다.

$E = [t]_{\times}R = Udiag(1,1,0)V^T$

이를 최종적으로 아래와 같이 factorization할 수 있다.

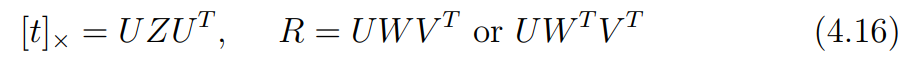
강의 노트의 나머지 내용은 잘 이해하지 못했습니다.. 결론만 추측해보겠습니다.

앞서 보았듯이 $R$은 두개의 값을 가질 수 있다.
또한 $[t]_\times$ 역시 여러 종류의 값을 가질 수 있는데, cross product의 성질을 이용해 이를 구할 수 있다.

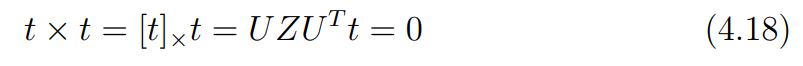
$U$는 유니터리 행렬이기 때문에 $t$는 scale 없이 방향만을 고려하는 단위벡터이고, 이를 바탕으로 $\|[t]_\times\|_F = \sqrt{2(t_x^w + t_y^2 + t_z^2)} = \sqrt{2}$ 라는 것을 알 수 있다.

때문에 위 식들과, E가 up to scale임을 고려하면 $t$를 아래 식과 같이 factorization 할 수 있다.

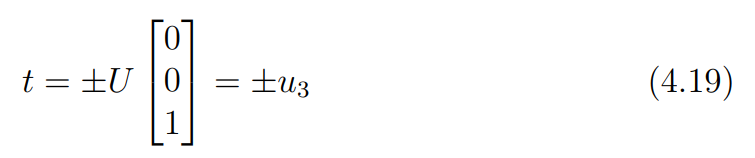
즉 $t$ 역시 두 종류의 값을 갖는다.
최종적으로 $t, R$은 4가지의 경우를 갖게 된다.

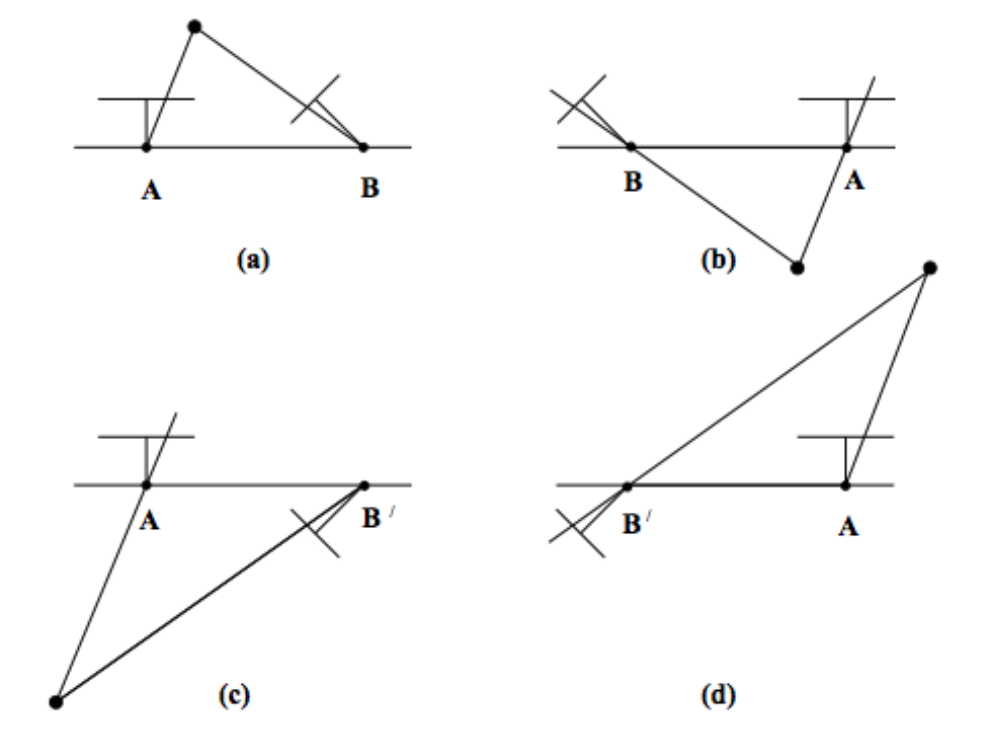
올바른 $\hat{P}$는 카메라 앞에 있어야 하므로 $z$ 좌표값이 두 카메라 모두에서 양수여야 한다.
즉 위의 figure에서는 (a)가 올바른 $t, R$ 쌍임을 알 수 있다.

이상적인 조건에서는 위와 같이 하나의 triangulating 만으로도 $R, t$ 쌍을 찾을 수 있지만, 현실에서는 측정 노이즈 등으로 인해 여러개의 점을 바탕으로 $R, t$를 결정한다는 것을 알아두자

5. An example structure from motion pipeline

이렇게 구한 $R, t$로 상대적인 motion matrix $M_i$값을 찾았다면, 이를 바탕으로 $X_j$를 구할 수 있다.
하지만 $\hat{P}$는 투영 변환 $H$가 적용된 것이고, $E$가 up to scale이기 때문에 절대적인 scale없이 방향과 형태만 알 수 있다는 점에 주의하자.

한 쌍의 카메라가 아니라, 보다 많은 multi-view case로 이를 확장하려면, Bundle adjustment를 통해 카메라 쌍을 chaning하는 방법을 사용할 수 있다.

5.1 Bundle adjustment

앞서 설명한 방법들을 이용해 SfM 문제를 푸는 것엔 한가지 큰 한계가 있는데, 모든 이미지에 복원하고자 하는 point가 존재해야한다는 것이다. 현실적으로는 각도의 차이나, occlusion 등으로 인해, point를 매칭하는 것이 어렵다.

이러한 한계를 극복하기 위한 방법이 bundle adjustment이다.
bundle adjustment는 재구성한 3D point들을 재투영하여 실제 이미지와의 pixel distance를 기반으로 한 reprojection error를 최소화하는 nonlinear optimization method이다.

즉 해당 카메라에 보이는 point들에 대해서만 error를 계산하기 때문에 이전의 algebraic approach와 달리 모든 point가 대응되지 않아도 된다.

bundle adjustment 문제를 풀기 위해 주로 Gauss-Newton 알고리즘과 Levenberg-Marquardt 알고리즘을 이용한다.

하지만 bundle adjustment는 한가지 중요한 문제가 있는데, minimization 문제인 만큼 local minimization에 빠질 우려가 있어 초기값을 잘 설정하는 것이 매우 중요하다.
때문에, SfM 문제에서 초기에는 factorization이나 algebraic approach를 사용해 어느정도 정확한 initial solution을 구해놓고, SfM의 마지막 단계에서 bundle adjustment로 정확한 해를 구하는 구하는 방식을 사용한다.

정리

SfM은 multi view 2D 이미지로부터 3D 씬 정보를 복원하는 알고리즘이다.

이번 강의 노트를 통해 SfM이 어떤 원리, 과정을 통해 multi view 이미지를 복원하는지 triangulation부터 bundle adjustment까지 배울 수 있었다.

참고 자료

[블로그]CH04. Stereo Systems