DMTet은 저해상도의 voxel 또는 포인트 클라우드를 고해상도의 삼각형 mesh로 변환할 수 있는 hybrid representation입니다.
여기서 hybrid라고 하는 이유는 voxel이라는 explicit representation과 signed distance field라는 implicit representation을 동시에 사용하기 때문입니다.
1. 3D Representation
DMTet은 DefTet에서 제시한 변형 가능한 사면체 그리드를 적용하였습니다.
그리드의 각 단위 사면체는 4개의 정점(vertex)과 면(face)으로 구성됩니다.
그리드를 구성하는 사면체 중 표현하고자 하는 오브젝트의 표면에 위치하는 표면 사면체만이 오브젝트의 3D shape을 표현하는 것에 기여합니다.
여기서 표면 사면체를 구분하기 위해 SDF값을 사용합니다.
1.1 Deformable Tetrahedral Mesh
사면체를 구성하는 각 정점은 자신의 3D 위치()외에 SDF값()을 갖고 있습니다.
특정 point의 SDF값을 알고싶다면, point가 위치한 사면체의 정점으로부터 SDF값을 가져와 무게중심 보간(barycentric interpolation)하여 근사하는 식으로 얻을 수 있습니다.
1.2 Volume Subdivision
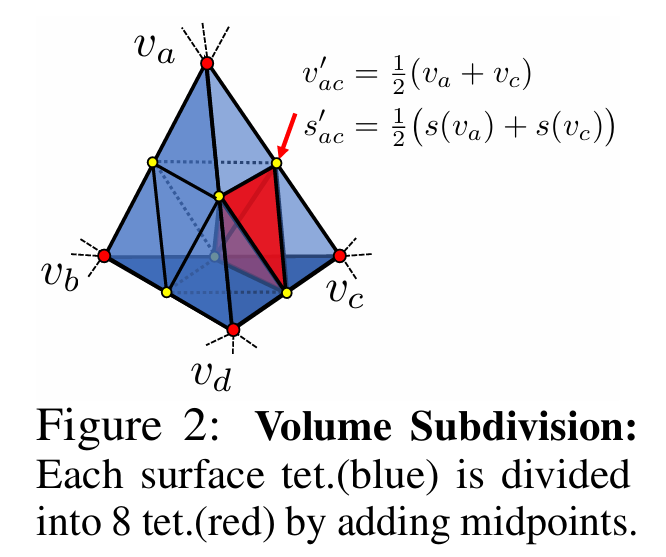
저해상도의 표현으로부터 고해상도의 3D 형상을 얻어야 하므로, coarse to fine manner를 적용합니다.
Figure 2에 나타난 것처럼 사면체를 구성하는 각 엣지의 중심을 기준으로 총 8개의 사면체로 세분화가 가능합니다.
앞서 설명했듯이 표면 사면체만이 3D shape에 기여하기 때문에, 세분화 된 후 표면 사면체에 속하지 않는 사면체는 제거됩니다.
1.3 Convert Surface Shape
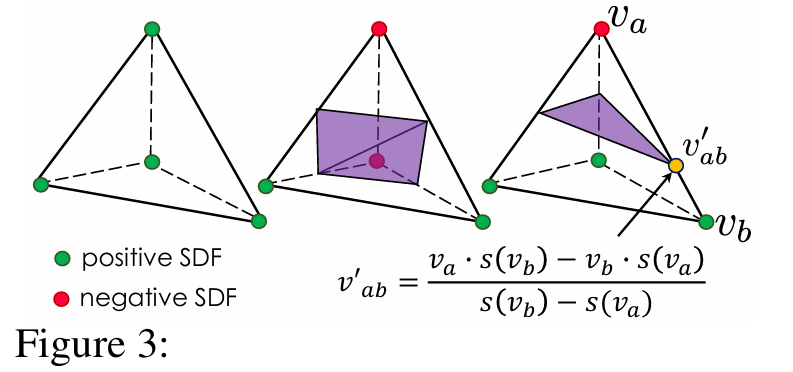
표면 사면체들을 삼각형 mesh로 변환하기 위해서는, 각 사면체가 어떤 shape을 나타내는지 결정해야 합니다.
기존의 Marching Cube 알고리즘에서는 occupancy를 통해 정해진 갯수의 모양 중 하나를 선택하는 방식이었지만, Marching Tetrahedra(MT)에서는 SDF 값을 바탕으로 다양한 모양의 삼각형 polygon을 정의할 수 있습니다.
Figure 3에도 잘 나타나 있으며, 구체적인 코드는 다음과 같습니다.
"""
edges_to_interp : 표면 edge의 vertex position
edges_to_interp_sdf : 표면 edge의 SDF값
"""
edges_to_interp = pos_nx3[interp_v.reshape(-1)].reshape(-1,2,3)
edges_to_interp_sdf = sdf_n[interp_v.reshape(-1)].reshape(-1,2,1)
edges_to_interp_sdf[:,-1] *= -1
denominator = edges_to_interp_sdf.sum(1,keepdim = True)
edges_to_interp_sdf = torch.flip(edges_to_interp_sdf, [1])/denominator
verts = (edges_to_interp * edges_to_interp_sdf).sum(1)여기서 표면 엣지는 부호가 서로 다른 두 정점을 잇는 엣지를 말합니다.
Figure 3에도 나와있듯이 표면 shape을 계산하기 위해서 표면 엣지만 사용하기 때문에 위 코드에는 생략되었지만 별도의 필터링 과정을 거칩니다.
나머지 코드는 Figure 3에서 를 구하기 위한 계산식을 적용한 것입니다.
v = torch.tensor([[[-1, -1, -1], [0, 1, 2]]])
s = torch.tensor([[[-1.5], [1]]])
s[:, -1] *= -1
denominator = s.sum(1, keepdim=True)
s = torch.flip(s, [1]) / denominator
verts = (v * s).sum(1)
print(verts)
>>> tensor([[-0.4000, 0.2000, 0.8000]])실제로 값을 넣어보면 두 표면 엣지(v[0], v[1]) 사이의 verts값을 잘 구한 것을 확인할 수 있습니다.
모든 사면체에 이러한 과정을 반복해 구한 삼각형 polygon들을 이으면, 빈틈 없는 삼각형 표면 mesh를 얻을 수 있습니다.
1.4 Surface Subdivision
논문에 의하면 이렇게 구한 표면 mesh에 differentiable surface subdivision module을 적용하면 mesh의 품질을 향상시킬 수 있다고 합니다.
이에 관해서는 논문의 appendix에서 자세히 다루었다고 하는데, 여기까지는 다루지 않겠습니다.
2. DMTet
앞서 사면체 그리드를 표면 mesh로 변환하는 과정에 대해 알아보았습니다.
이번 섹션에서는 input을 받아 고해상도의 삼각형 mesh를 생성하는 모델에 대해 구체적으로 알아보겠습니다.

2.1 3D Generator
먼저 복셀 또는 포인트 클라우드를 입력받아 고해상도의 mesh를 생성하는 모델의 구조를 알아보겠습니다.
Input Encoder
우선 입력을 포인트 클라우드 형식으로 통일합니다. 복셀이 입력된 경우 표면으로부터 point를 샘플링하여 포인트 클라우드로 변환합니다.
변환된 포인트 클라우드에서 PVCNN이라는 인코더를 통해 3D Feature Volume 을 얻습니다.
사면체 그리드를 구성하는 각 정점의 feature vector 는 feature volume으로부터 trilinear interpolation을 수행하여 계산할 수 있습니다.
Initial Prediction of SDF
MLP를 통해 각 정점의 위치, feature vector를 입력으로 정점의 SDF값 과 를 예측합니다.
여기서 는 추후 surface refinement에서 사용될 것이라 합니다.
Surface Refinement with Volume Subdivision
예측한 SDF값을 통해 표면 사면체 를 식별합니다.
표면 사면체의 각 정점 및 엣지를 모아 그래프 를 구성합니다.
이 그래프와 정점에 대한 정보를 나타내는 feature vector 를 GCN의 입력으로 사용해 사면체가 표면을 더 잘 표현할 수 있도록 그리드를 변형시키는 오프셋값 를 예측합니다.
변형 후의 각 정점은 , 으로 업데이트 됩니다.
추가로 앞서 구한 역시 GCN의 출력값 중 일부인 로 교체됩니다.
이러한 방식의 업데이트는 오프셋값을 기반으로 하기 때문에 각 정점의 SDF 부호가 바뀌는 등 비교적 자유로운 변형이 가능하기 때문에, local geometry를 잘 개선할 수 있다고 합니다.
또한 각 surface refinement 단계 사이에 volume subdivision(1.2)을 거쳐 점점 고해상도가 됩니다.
3.2 3D Discriminator
이제 예측에 사용되었던 모델을 최적화하기 위한 loss를 구해야 합니다.
DMTet에서는 이 역할을 DECOR-GAN의 discriminator가 수행한다고 합니다.
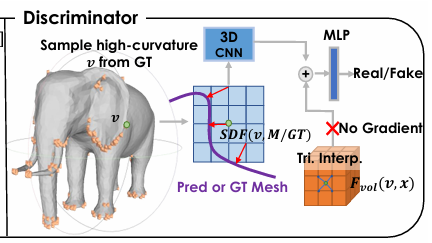
Figure 4에 묘사된 것 처럼 GT를 복셀화하여 곡률이 높은 포인트 를 랜덤하게 선택하고, GT signed distance field 을 계산합니다.
비슷하게, 예측한 mesh 에서 위치에 해당하는 signed distance filed 를 계산합니다.
계산된 두 signed distance field와 GT로 부터 인코딩하여 구한 를 함께 넣어 discriminator가 판별하게 합니다.
이를 통해 GT shape와 예측된 mesh가 유사해지도록 모델을 개선하는 adversarial loss를 얻을 수 있습니다.
Loss Function
DMTet의 loss는 총 3가지의 term으로 구성됩니다.
- Adversarial loss
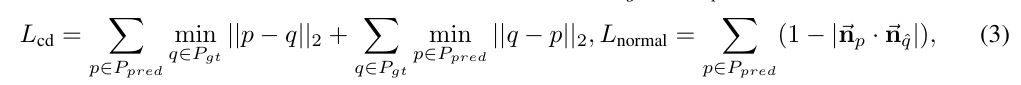
- GT 표면과 정렬되도록 유도하는 surface alignment loss
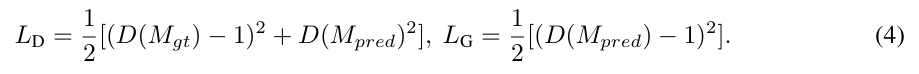
- SDF값과 vertex position이 덜 변형되도록 하는 regularization term
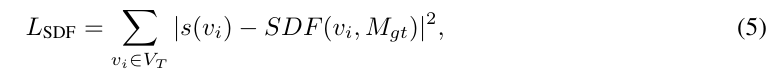
가 필요한 이유는, SDF값을 기반으로 표면을 추출하여 loss를 계산하는데, 앞서 계산한 두 loss는 SDF값의 부호를 바꾸어도 똑같은 결과가 나온다고 합니다. (어디가 바깥이고 안쪽인지를 고려하지 않음)
이로인해 학습 도중에 SDF값의 부호가 바뀌어 뒤틀린 mesh가 결과로 나올 수 있게 됩니다. 때문에 초기값에서 너무 멀어지지 않도록 하는 SDF loss를 적용한 것입니다.
여기에 더해 artifacts가 발생하는 것을 막기 위해 vertex 변형에 대한 regularization term도 적용했다고 합니다.
최종 loss는 다음과 같습니다.
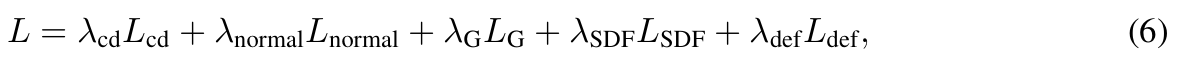
여기서 람다값은 하이퍼파라미터입니다.
코멘트
이렇게 DMTet이 어떻게 고해상도의 3D mesh를 추출하는지 간단하게 다루었습니다.
사실 논문에 대해서도 보다 깊게 이해하고 코드도 자세히 뜯어보고 싶었으나, 아직 배워야 할 것이 너무 많기에.. Neus나 Tetrahedron Splatting과 같은 이후 연구들을 이해하는데 지장이 없을 정도로만 짚고 넘어가려 합니다.
