
Linear Equation(선형 방정식)
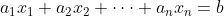
- n개의 변수(
x)로 이루어진 선형방정식은 위와 같이 쓸 수 있다. - 여기서
b는 선형방정식의 결과에 해당하는 상수,a는 계수이다.
선형방정식의 벡터 표현
- 선형방정식은 계수를 성분으로 갖는 벡터
a와 변수를 성분으로 갖는 벡터b두 벡터의 내적으로 나타낼 수 있다. - 이 때 내적을 위해 a를 transpose한 행벡터로 만들어 사용한다.
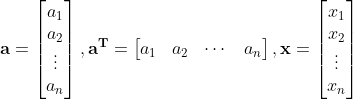
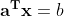
Linear System
- Linear system은 선형방정식의 집합이라 할 수 있다.
- 방정식으로 풀어 설명하면 Linear system은 n개의 변수와 m개의 방정식으로 이루어진 연립방정식이다.
60x + 5.5y + z = 66
65x + 5.0y = 74
55x + 6.0y + z = 78
위 연립방정식은 다음과 같이 나타낼 수 있다.
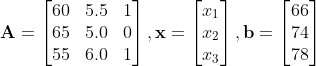
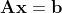
그렇다면 위 식을 만족하는 x는 어떻게 풀 수 있을까?
Identity Matrix (항등행렬)
- 항등행렬은 대각선 성분이 1이고, 나머지 성분이 0으로 이루어진 정사각 행렬을 말한다.
- 어떤 행렬과 항등행렬을 곱하면 행렬 자기자신이 결과로 나온다.
- I로 표기한다. (
n x n의 항등행렬은In)
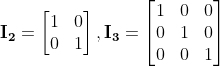
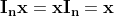
Inverse Matrix (역행렬)
- 정사각 행렬에서 어떤 행렬 A에 곱하면 항등행렬이 되도록 만드는 행렬을 역행렬이라 한다.
- A의 역행렬은
A^{-1}로 표기한다.
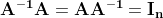
역행렬의 존재여부
- 어떤 행렬에 대한 역행렬의 존재여부는 determinant(
detA, 행렬식) 라는 값을 통해 알 수 있다. 2x2의 경우 행렬식은 다음과 같다.

detA = 0인 경우 역행렬이 존재하지 않는다.- 또한
detA는 선형 변환에서 기존 데이터(vector)의 길이를 얼마나 확대(또는 축소)했는지의 정도를 배수로 나타낸다.
역행렬의 의의
- 선형방정식을 다음과 같이 풀 수 있다.
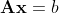
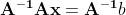
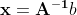
- 이때 역행렬이 존재한다면 x는 유니크한 해를 갖는다. (해를 딱 1개만 갖는다)
- 역행렬이 존재하지 않는다면 x의 해는 존재하지 않거나, 무수히 많게 된다.
직사각 행렬(Rectangular Matrix)의 역행렬
- 수학적으로 역행렬은 오직 정사각 행렬에서만 논할 수 있다.
- 다만 직사각 행렬에서도 곱했을 때 항등행렬이 되도록 만드는 행렬이 존재할 수 있다.
- 이 경우는 별도로 정의하며, 역행렬과 달리 행렬곱 순서가 바뀌면 성립하지 않는다.
- 이번 강의에서는 자세히 다루지 않는다.
Rectangular Matrix in Linear System
60x + 5.5y + z = 66
65x + 5.0y = 74
55x + 6.0y + z = 78
70x + 5.0y + z = 55
- 위와 같이 정해졌을 때 A 행렬은
4 x 3이 된다. - 여기서 행의 개수(m)는 방정식의 수를 의미하고, 열의 개수(n)는 미지수(변수)의 개수를 의미한다.
- m ≠ n이라면 행렬은 직사각 행렬이 된다.
m > n의 경우
- 미지수보다 방정식(수집된 데이터의 수)가 많은 경우이다.
- 이 경우 보통 모든 방정식을 만족하는 해는 존재하지 않는다.
- 하나의 해를 구할 수 없지만, 각각의 b에 가장 근사할 수 있는 해를 구하게 된다.
m < n의 경우
- 수집된 데이터의 수보다 미지수(알아야 하는 feature) 개수가 많은 경우이다.
- 이 경우 무수히 많은 해가 존재한다.
- regularization을 이용하여 무수히 많은 해중 목표에 최적화된 해를 구하게 된다.
결론
- 머신러닝의 문제는 방정식의 문제로 환원할 수 있다.
- rectangular matrix에서도 방정식의 해를 구할 수 있다.
