[백준] 28706. 럭키세븐

cjkangme·2023년 8월 14일

DP 알고리즘

Algorithm

목록 보기

34/35

문제 : https://www.acmicpc.net/problem/28706

문제 설명

T개의 테스트 케이스가 주어진다. (1 ≤ T ≤ 10,000)
각 테이스 케이스 별로 N개의 명령어가 주어진다. (1 ≤ N ≤ 200,000)
각 명령어는 2개의 연산으로 구성되어있다.

문제는 1부터 시작하여 각 명령어에서 연산 하나를 골라 끝까지 수행했을 때 7의 배수가 되는 경우가 존재하는지 찾는 문제이다.

각 명령어 당 선택지가 2개이므로 단순 계산하면 2 ** N 가지의 경우의 수를 고려해야한다.

예시

예제
2
+ 3 + 6
+ 1 + 2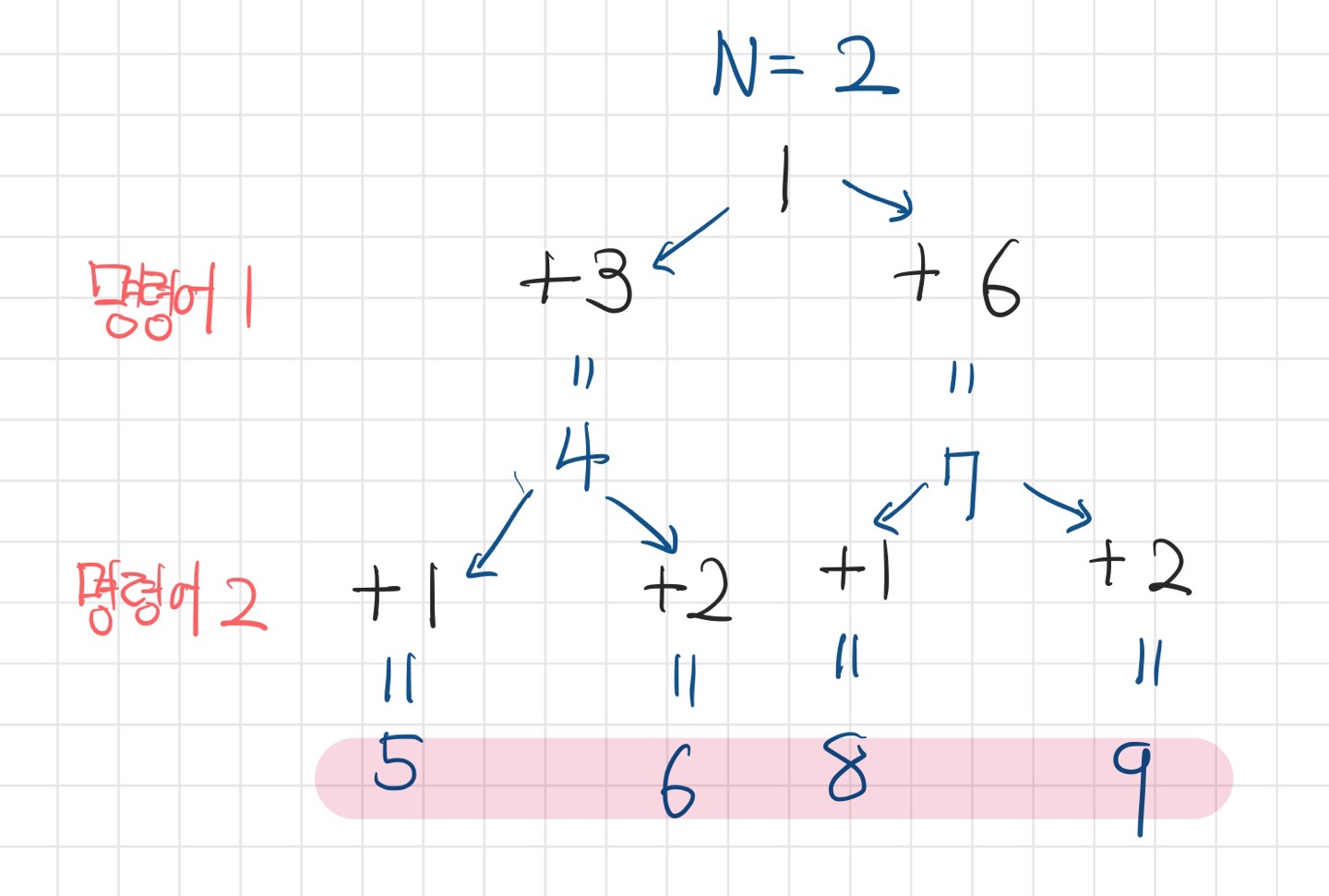

위 예제를 입력받았을 때 연산은 다음과 같다.

N=2개의 명령어를 모두 수행한 뒤 7의 배수가 존재하지 않으므로 출력은 UNLUCKY가 된다.

풀이

모든 수를 고려한다면 O(2^N)의 시간복잡도를 갖지만,
7의 배수인지만 확인하면 되므로 실제로는 O(N)의 시간복잡도로 풀 수 있다.

바로 연산 결과를 저장할 때 mod 7의 결과를 저장하여 저장하는 값의 범위가 0 ~ 6이 되도록 하는 것이다.
이러면 가능한 모든 경우의 수에 대해 for loop을 돌아도 7 * N번만 돌면 된다.

마지막에는 저장된 값에 0이 있는지 확인하여 있다면 LUCKY를 출력하면 된다.

이번 풀이에서는 중복값 저장 방지를 위해 set을 사용하였다.

예제

4
+ 3 * 1   ··· 1
+ 4 + 5   ··· 2
* 9 * 2   ··· 3
* 6 + 3   ··· 4

1

set : {1}

연산
(1 + 3) % 7 = 4
(1 * 1) % 7 = 1

연산 후
set : {1, 4}

2

set : {1, 4}

연산
(1 + 4) % 7 = 5
(1 + 5) % 7 = 6
(4 + 4) % 7 = 1
(4 + 5) % 7 = 2

연산 후
set : {1, 2, 5, 6}

3

set : {1, 2, 5, 6}

연산
(1 * 9) % 7 = 2
(1 * 2) % 7 = 2
(2 * 9) % 7 = 4
(2 * 2) % 7 = 4
(5 * 9) % 7 = 3
(5 * 2) % 7 = 3
(6 * 9) % 7 = 5
(6 * 2) % 7 = 5

연산 후
set : {2, 3, 4, 5}

4

set : {2, 3, 4, 5}

연산
(2 * 6) % 7 = 5
(2 + 3) % 7 = 5
(3 * 6) % 7 = 4
(3 + 3) % 7 = 6
(4 * 6) % 7 = 3
(4 + 3) % 7 = 0
(5 * 6) % 7 = 2
(5 + 3) % 7 = 1

연산 후
set : {0, 1, 2, 3, 4, 5, 6}

마지막 명령어까지 연산 수행 후 set에 0이 존재하므로 7의 배수가 존재한다는 것을 알 수 있다.
LUCKY를 출력한다.

코드

import sys

input = sys.stdin.readline

def calculate(command, dp_set):
    temp = set()
    for i in range(0, 4, 2):
        oper, num = command[i], command[i+1]
        for operand in dp_set:
            if oper == "+":
                temp.add((operand + int(num)) % 7)
            else:
                temp.add((operand * int(num)) % 7)
    return temp

if __name__=="__main__":
    T = int(input())
    for _ in range(T):
        N = int(input())
        commands = [list(map(str, input().split())) for _ in range(N)]
        dp_set = set([1]) # 1부터 시작
        for command in commands:
            dp_set = calculate(command, dp_set)
            
        if 0 in dp_set:
            print("LUCKY")
        else:
            print("UNLUCKY")