Random Variables
Definition
Real numbers mapping each outcome of random expertiment to a real value
랜덤한 실험의 결과를 실제 값(실수)으로 map
ex)
w1, w2, ... in Sample space S
X(w) = x
x는 random variable
원래 A가 일어날 확률을 P(A)라 한다면 P(x)로 변환
이 때 x는 random variable
Discrete RV
non-continuous
확률변수가 연속적이지 않고 실수마다 확률 값이 정해짐
Continuous RV
RV is uncountably infinite
확률 변수가 셀 수 없을 만큼 무한하기 때문에
P(x=xi) 특정 xi에 대한 확률값을 정의할 수 없다.
P(0.5) = 0
Contradiction을 통해 해당 내용을 증명 할 수 있다.
if exists xi that a<xi<b , P(x=xi) = p (p는 임의의 실수)
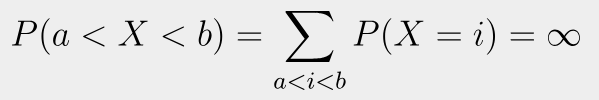
따라서 Continuous RV에서 확률을 도입하기 위해 pdf를 사용한다.
Distribution Function
Cummulative Distribution Function
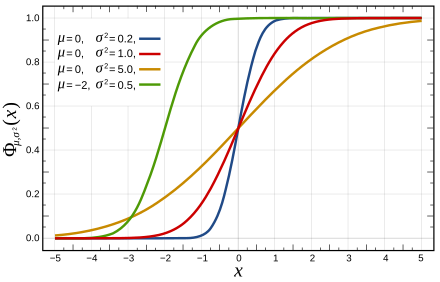
누적분포함수(CDF)
F(x) = P(X<=x)
F(1) = P(X<=1)
CDF의 성질
1) if x1<x2 -> F(x1) <= F(x2)
∵ 누적 분포 함수는 감소함수가 아니므로
2) 0 <= F(x) <= 1
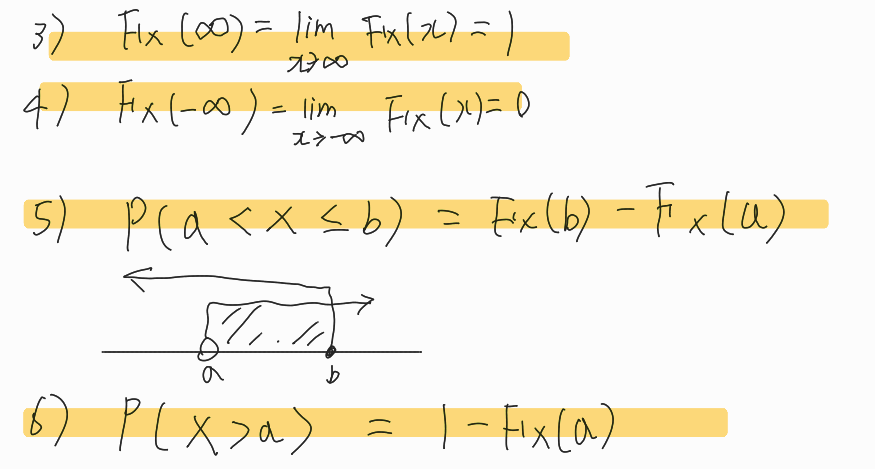
Discrete한 확률변수의 경우 equality의 주의 해야 한다.
Continious한 경우 equality와 관계없이 값에 차이가 x
Probability mass function

(PMT) 확률질량함수
Discrete RV에서 특정 값에 대한 확률을 나타내는 함수.
Probability Density Function과 대비
Definition
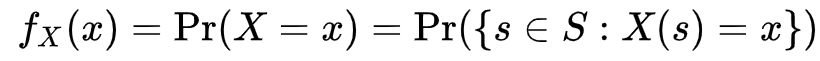
확률 변수 X가 sample space S의 이산 확률 변수일 때,
X=x일 확률: fx(x)
Probability Density Function
PDF 확률 밀도 함수
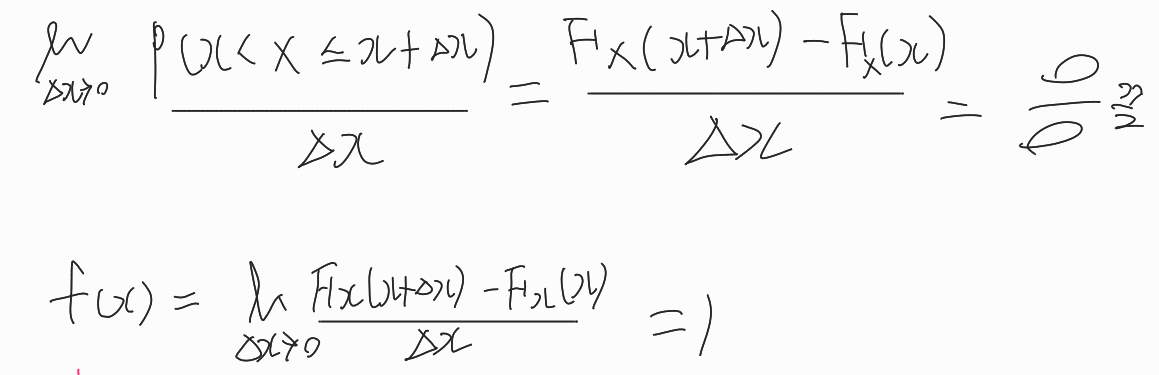
우리는 Continuous RV의 확률을 구하기 위해 x<X<x+Δx 사이의 구간을 정의하고 미분하면 X=x일 때 확률을 구할 수 있다. 엄연히 따지면 해당 지점의 확률을 구할 수 없지만 아주작은 구간을 정의하여 구할 수 있다.
따라서
확률밀도함수는 누적분포함수를 미분한 것이다.
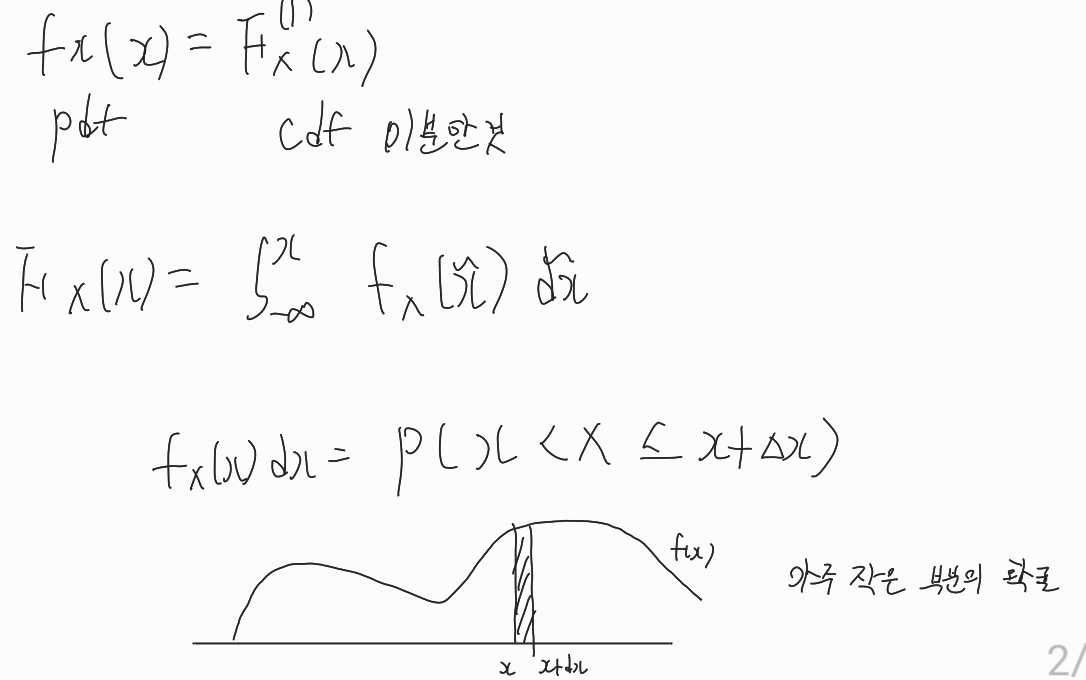
PDF의 성질
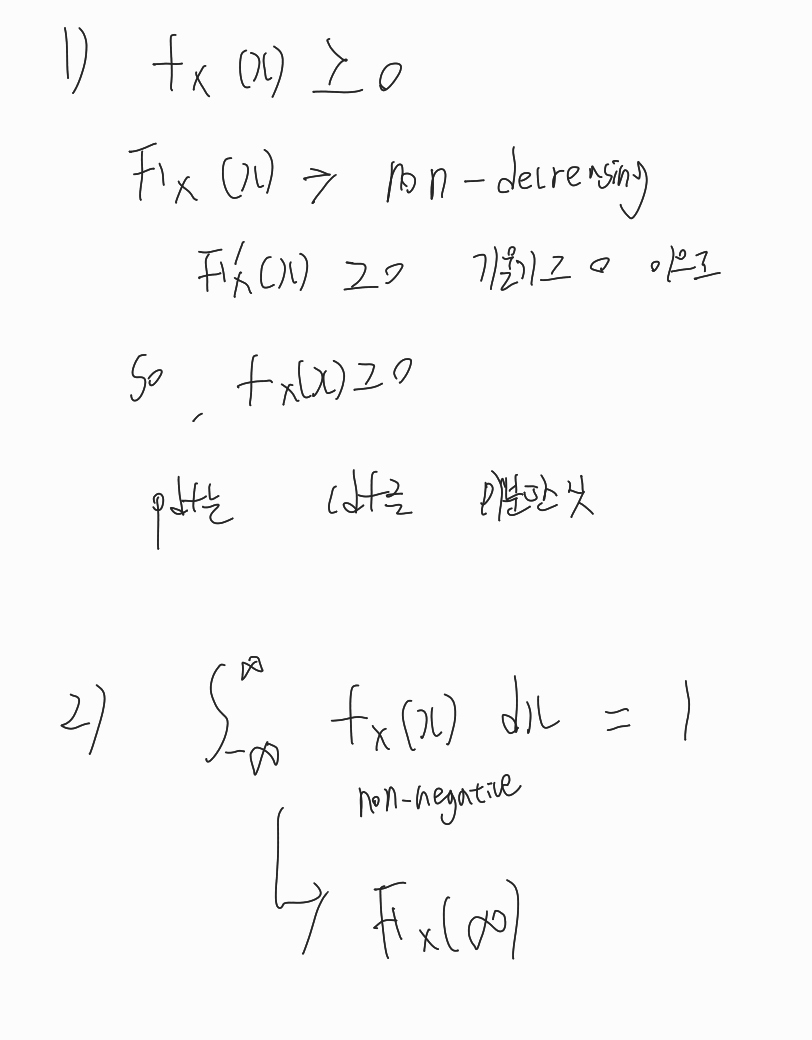
pdf가 되기 위해 1과 2를 만족
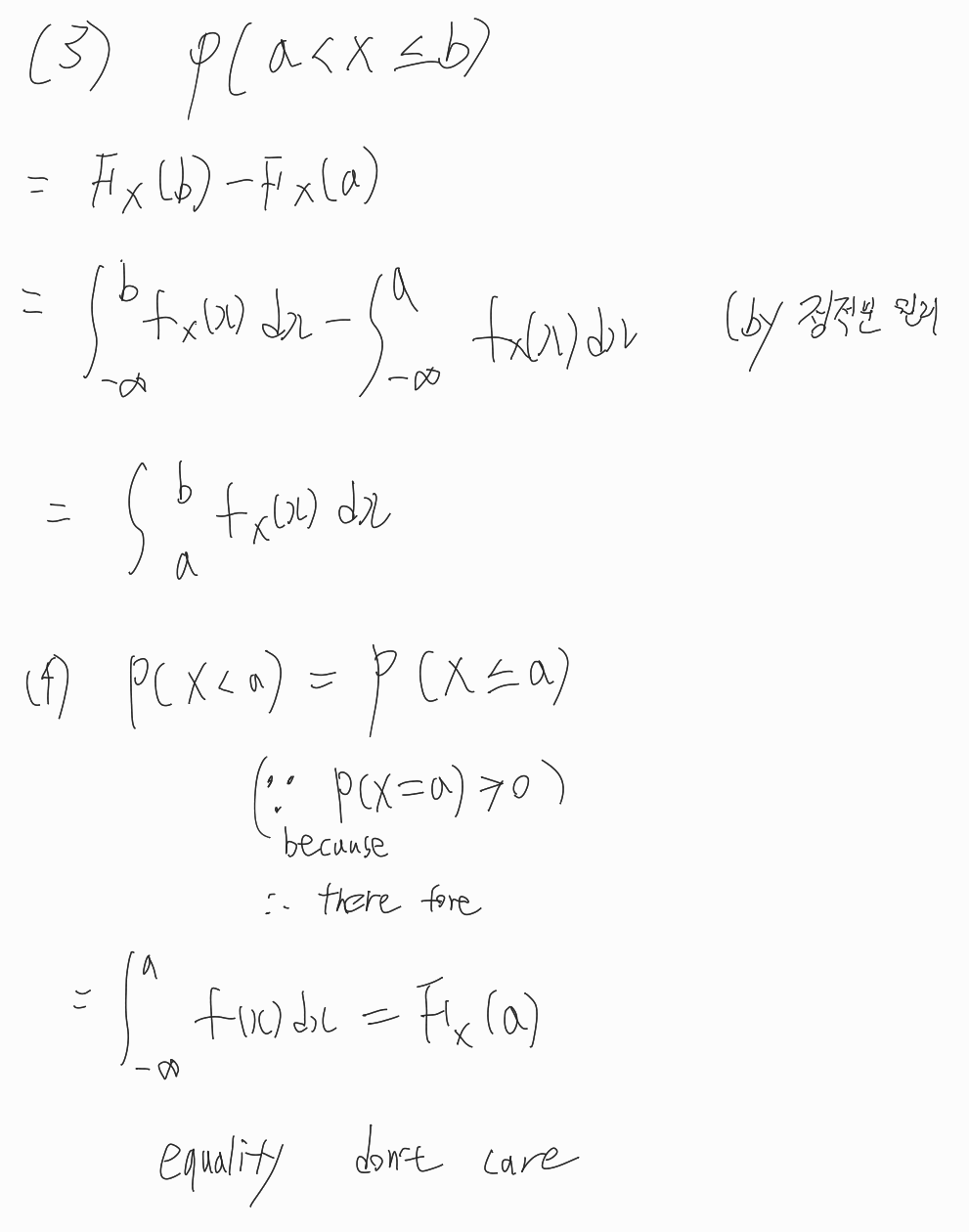
Uniform distribution
확률 밀도 함수가 상수값을 가질 때를 의미
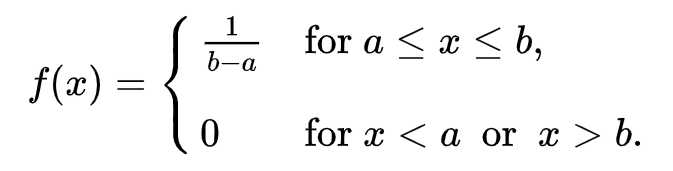
특정 구간 개구간 또는 폐구간에서 a와 b사이 확률밀도함수가 상수값이다.
조금만 생각해보면 a와 b사이 확률의 합은 1
cdf는
a지점까지 0,
b지점까지 함수값 1로 증가하는 일차함수,
b 지점부터는 계속 1인 상수함수 일 것이다.