Training Neural Networks_LG Aimers(13)

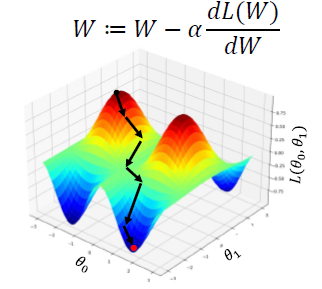
Gradient Descent

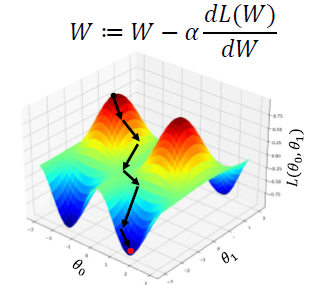
• neural network에서 최적화를 하고자 하는 parameter들과 학습 data를 parameter들로 이루어진 neural network에 입력으로 집어넣어서 ground truth 값과 비교함으로써 차이를 최소화하도록 하는 loss function을 만들었을 때, 이 loss function을 최소화하도록 하는 그러한 parameter를 찾는 것
• loss function에 대해 각 parameter들에 대한 미분 값을 구하고, 이를 이용하여 현재 주어진 parameter 값을 가지고 미분 방향의 마이너스 방향으로, 특정 step size를 이용하여 해당 parameter를 update한다.
• 함수의 출력 값은 loss가 된다.
• random initialize에서 함수의 높이가 점점 낮아지는 방향으로 해당 parameter 값들이 update된다.

Various Gradient Descent Methods

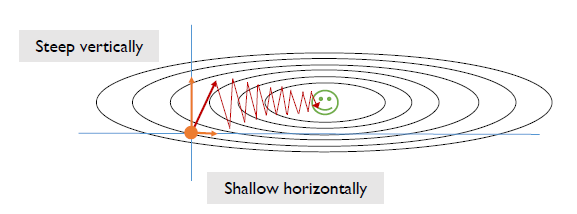
• original 방식을 사용할 때, loss function이 굉장히 복잡한 형태를 띄고 있다면 수렴 속도가 상대적으로 굉장히 느릴 수 있다.
• 여러 다양한 gradient algorithm 알고리즘이 존재한다.
• local minima에 도달할 수도 있다.

Back propagation

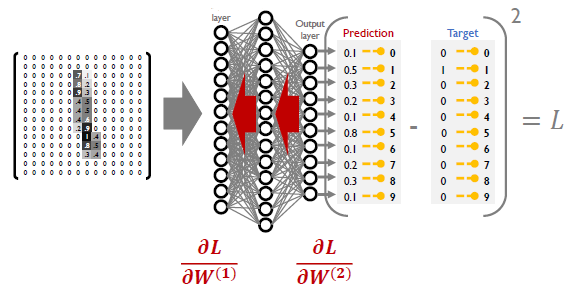
• 학습 data에 대해서 forward propagation을 수행하고, 이 때 사용되는 각 parameter들은 random initialization에서부터 시작한다.
• 그 때 나오는 예측된 값들은 물론 해당하는 입력 data의 ground truth 값과 상이하며, 이러한 차이를 계산하고 최소화하는 방향으로 손실함수를 정의한다.
• 손실함수를 편미분하고, 이러한 편미분 값을 통해 parameter들을 update해야한다.
• forward propagation을 통해 loss function을 정의하고, loss 값을 minimize할 수 있도록 back propagation 과정을 통해서 직접적으로 update할 parameter들에 대한 loss function의 gradient 값을 구하고 알고리즘을 통해 update를 수행한다.

Sigmoid Activation

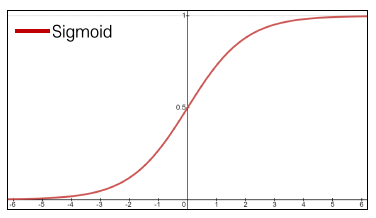
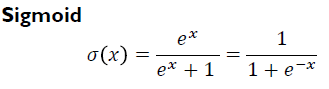
• 입력 perceptron이 선형 결합을 하여 만들어진 값이 이런 hard threshold를 적용해서 최종 출력 값을 내준 것을 부드러운 형태의 함수로 근사화 한 것
• 주어진 선형 결합의 결과가 $(-\infin, \infin)$까지 가질 수 있는 값들을 (0, 1) 사이의 값으로 mapping 시킨다.
• 해당 값을 예측된 확률 값으로 정의할 수 있다.

Gradient Vanishing

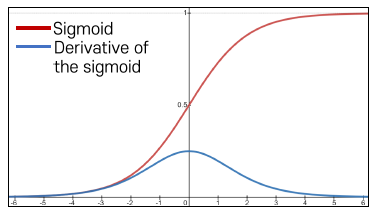
• gradient의 값이 최대 $1/4$까지만 가질 수 있게 된다.
• 이를 back propagation 할 때마다 output 값에서 계산되었던 gradient 값에 (0, 1/4)의 값을 곱해주게 되면서 입력 값의 gradient가 결정이 된다.
• 이러한 과정이 계속 될 때마다 gradient값이 계속 깎여 나가며 점차적으로 gradient 값이 0에 가까워지는 문제점이 발생한다.
• 특정 learning rate를 사용했을 때, 앞쪽의 gradient 값이 너무 작아 parameter들의 update가 거의 일어나지 않게 되는, 학습이 느려지는 문제가 발생한다.

Tanh Activation

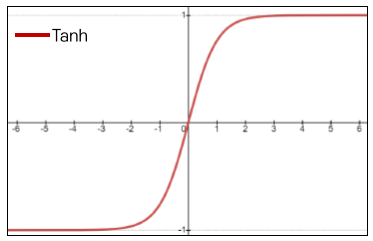
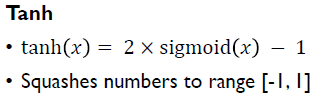
• gradient vanishing을 해결하기 위한 활성 함수
• sigmoid 함수에 두 배를 곱하고 -1을 취한 함수
• sigmoid 함수 대신 사용했을 때 값의 범위는 (-1, 1) 사이의 값으로 mapping을 시킨다.
• 평균적으로 볼 때, 평균값이 0을 중심으로 나오는 값이 된다.
• gradient 값이 최대 0에서 최대 1/2 값인 값을 가지게 되므로 gradient vanishing 문제를 가지게 된다.

ReLU Activation

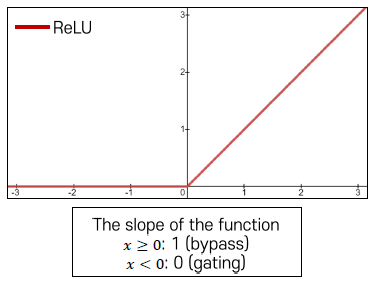
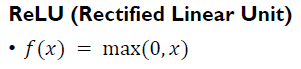
• $(0, \infin)$ 값을 mapping하므로, gradient vanishing 문제를 해결할 수 있다.
• 상대적으로 복잡한 연산에 비해 훨씬 더 빠르게 계산될 수 있다.
• 주어진 입력 값이 마이너스 값의 영역에 해당되었을 때는 해당 gradient는 접선의 기울기가 완전히 0이 나오기 때문에 gradient 값이 0이 되어서 이후의 gradient 값이 모두 0이 되는 문제점이 존재한다.

Batch Normalization

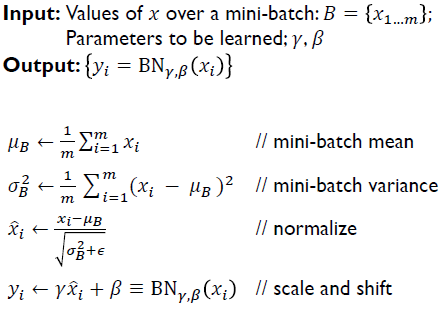
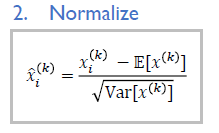
• 특정 활성 함수를 사용했을 때, 학습을 용이하게 하는 추가적인 특별한 형태의 뉴런 혹은 layer
• forward propagation을 할 당시에 다양한 활성 함수들의 입력으로 주어지는 값들의 대략적인 범위를 0 근처 혹은 범위로 제한할 수 있는 방법으로 gradient vanishing 문제 없이 학습을 용이하게 잘 할 수 있다.
• 하나의 mini batch가 특정 노드에서 활성 함수를 통과하기 직전에 값들의 평균, 분산을 계산하고 평균이 0, 분산이 1이 되도록 하는 정규화 과정을 수행한다.
• 이러한 변환을 통해 특정한 layer와 특정한 노드에서 발견되는 값들의 분포를 원하는 정해진 분포로 따르도록 만들어준다.

Batch Normalization process

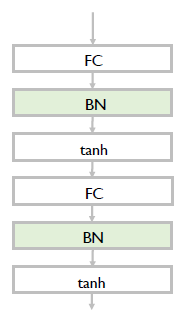
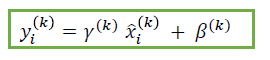
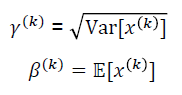
• fully-connected layer 혹은 선형 결합을 수행한 이후, 활성 함수로 들어가기 직전에 추가하는 형태가 일반적이다.
• 이러한 경우 fully-connected layer를 통과하며 만들어진 출력 값들이 고유한 평균과 분산을 가지고 있고, 이 또한 학습해야하는 중요한 값인 경우 무시할 수 없기 때문에 문제가 될 수 있다.
• 이렇게 무시된 정보를 원하는 정보로 복원할 수 있게 하는 두 번째 단계가 batch normalization에 존재한다.
• 평균, 분산을 각 0, 1로 만든 값에 neural network이 gradient descent를 통한 학습에 의해 최적화 한 parameter들을 도입하여 y=ax+b의 변환을 수행하는 추가적인 layer를 두 번째 단계로 삽입한다.