[논문 리뷰] Attention is All you need

찬호·2023년 11월 27일

자연어처리 논문 리뷰

목록 보기

3/21

Preface

우리는 앞에서 딥러닝의 기초부터 시작해서 자연어처리의 기계 번역을 담당한 seq2seq와 다양한 attention의 기법에 대해서 배웠습니다. 이제는 자연어처리의 시작인 Transformer 논문을 리뷰해보겠습니다.

Motivation

RNN와 LSTM이 가지는 장기 의존성 문제나 기울기 소실 문제등은 자연어처리에서 큰 문제였습니다. 그리하여 Attention 기법을 통하여 이에 대한 부담을 줄였지만, 이는 본래의 문제를 해결할 수는 없었습니다. 그리하여 구글 브레인 팀은 Attention 기법만을 사용한 Transformer을 만들어서 RNN와 LSTM의 학습 구조에서 탈출하게 되었습니다.

1. Introduction

RNN와 LSTM 등을 통한 NMT의 발전이 있었지만, 시퀀스를 학습할 때의 계산 시간이 많았습니다. 어텐션 메커니즘은 학습 단어와 관련된 단어들을 더 집중하여, 학습하게 해주었지만 이전의 어텐션 메커니즘들은 모두 RNN와 LSTM 등 recurrent network와의 결합으로만 나왔었기에 효율적이지 못했습니다. 특히 이러한 RNN계열의 아키텍처들은 이전 timestep의 hidden state가 현재 timestep의 input으로 들어오는 순차성 때문에 병렬화가 어려워 학습 속도가 느려지고, 성능이 하락하는 단점이 있습니다.

위 논문에서는 recurrent 네트워크를 피하고, 온전히 어텐션 메커니즘을 통해서만 학습을 진행하는 Transformer를 제안합니다.

2. BackGround

이 당시에도 sequential computation을 줄이기 위하여, Extended Neural GPU, ByteNet and ConvS2S와 같은 아키텍쳐들이 만들어졌지만, 두 input position과 output position를 relate 시키기 위해 필요한 작업량이 점점 늘어나는 경향이 있었습니다. (ConvS2S는 선형적으로, ByteNet은 지수적으로)

반면 Transformer는 이런 두 position 간의 거리를 가까워지게 하기 위한 작업을 상수번만 진행했다. 이 과정에서 타 model 대비 부족해지는 effective resolution의 경우에는 Multi-Head-Self-Attention으로 대응한다고 한다.

3. Model Architecture

이전의 아키텍쳐들에서 Encoder는 input data를 $(x_{1}, x_{2}, x_{3}, \ldots, x_{n})$ 으로 표현하여, $\mathbf{Z} = (z_{1}, z_{2}, \ldots,z_{n})$ 로 바꾸어 주는 작업을, Decoder는 $\mathbf{Z}$ 가 주어졌을 때, 한 번에 output인 $(y_{1}, y_{2}, y_{3} \ldots, y_{m})$ 을 만들어 냅니다. 이러한 모델들은 auto-regressive한 성질을 가졌는데, 과거와 현재의 데이터를 계속적으로 사용하는 것을 의미합니다.

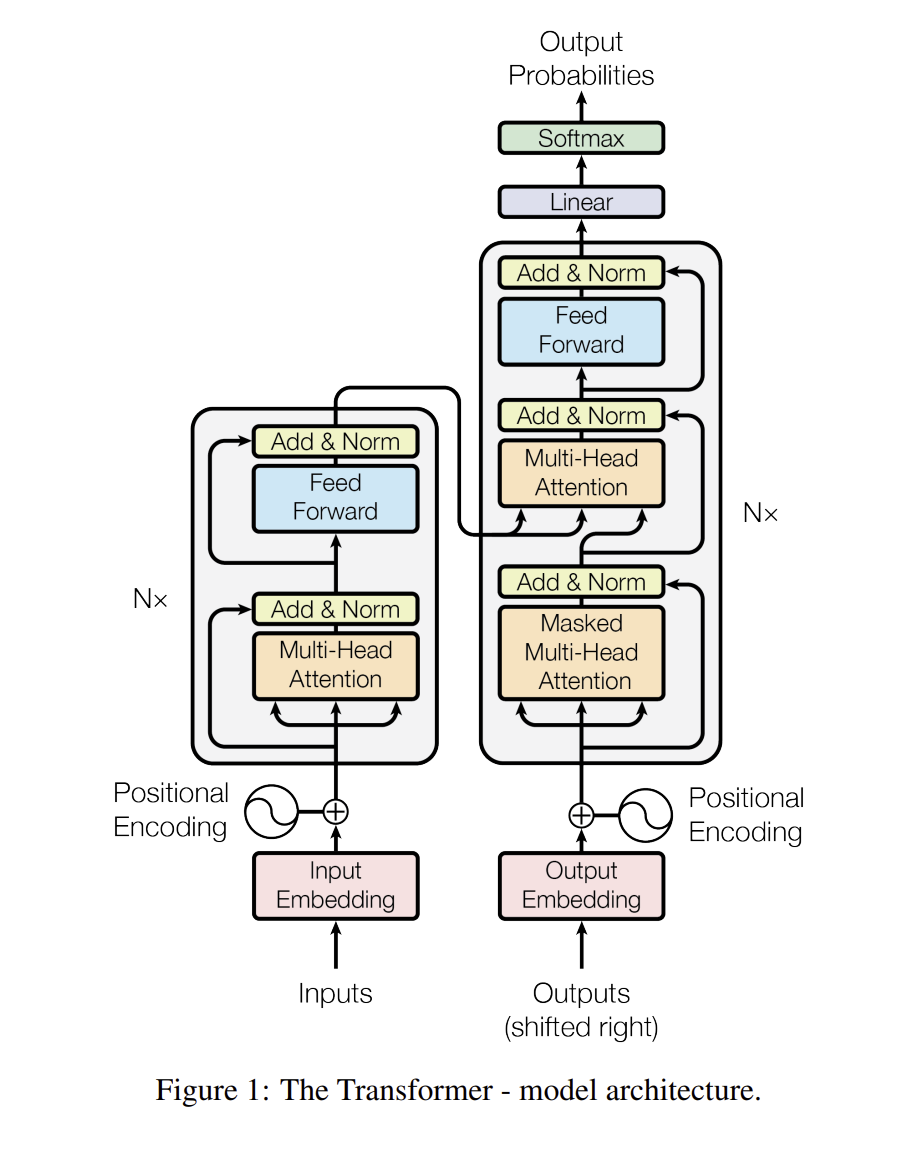
3.1 Encoder and Decoder Stacks

Encoder : 본 논문에서는 6개의 layer로 encoder를 쌓고, 각 sub_layer 마다 multi-head-self-attention과 feed-forward network로 구성되어 있다. 그리고 2개의 sub_layer 마다 Residual connection을 사용하여 layer normalization을 진행하고 있다.

여기서 Residual connection의 데이터는 기존의 데이터 Layer Norm(X와 Sublayer(X)) 으로 나오게 된다. 모델의 output 차원은 512차원!

데이터의 병렬화는 ‘I am good’ 이라는 문장을 RNN에서는 ‘I’를 받아야 ‘am’을 받고, ‘am’을 받아야 ‘good’ 을 받는 구조인데 병렬화가 가능하면 ‘I am good’ 을 한번에 입력 가능하여 속도가 굉장히 빨라진다는 의미이다.

Residual connection 이란?

Definition : 아주 deep 한 신경망의 정보가 기울기 소실과 폭발 문제로 잘 입력이 안되는 경우, 일부 레이어를 건너 뛰어, 데이터가 신경망의 구조의 후반부에 도달하는 다른 경로를 제공하는 방법!)

과정을 정리해보자면,

positional encoding으로 X로 구성된 input data의 순서를 알아낸다.
multi_head-self-attention와 residual connection을 거친다.
feed-forward network와 residual connection을 거친다

Decoder : 본 논문에서는 Encoder과 같이 6개의 layer를 쌓고, Decoder에는 3개의 sub_layer를 넣게 된다(Encoder는 2개). 각 sub_layer에는 multi-head-attention 2개와 feed-forward network 1개로 구성되어 있다.

다만 Encoder와 다른 점은 Decoder에 들어오는 $y$ 데이터들은 Masked-multi-head-attention을 이용한다는 점이다. Masked(가려진) mult-head-attention의 특징은 시계열 데이터의 성향상 t번째의 데이터를 학습할 때는 $y_{t-1}, y_{t-2}, y_{t-3}$ 의 데이터를 학습하는 건 맞지만 $y_{t+1}, y_{t+2}$ 등 미래에 나올 단어들을 판단을 하면 안되기에, 미래의 데이터를 masked(가려서) 해서 학습을 진행하는 것이다.

과정을 정리해보면,

Decoder에 들어갈 $y_{data}$ 들은 maksed-multi -head- attention + residual connection 을 거친다.
Encoder에서 나온 $data$ 들과 1번에서 거친 데이터들은 multi-head-attention + residual connection을 거치게 된다.
이후 feed-forward network + residual connection를 거쳐서 output으로 나오게 되는 것이다.

3.2 Attention

기존의 논문에서 사용했던 어텐션 메커니즘이 아닌 위 논문에서는 self attention 기법을 이용하여 query, key, value값을 도출하여 attention 스코어를 계산하는 방식이다.

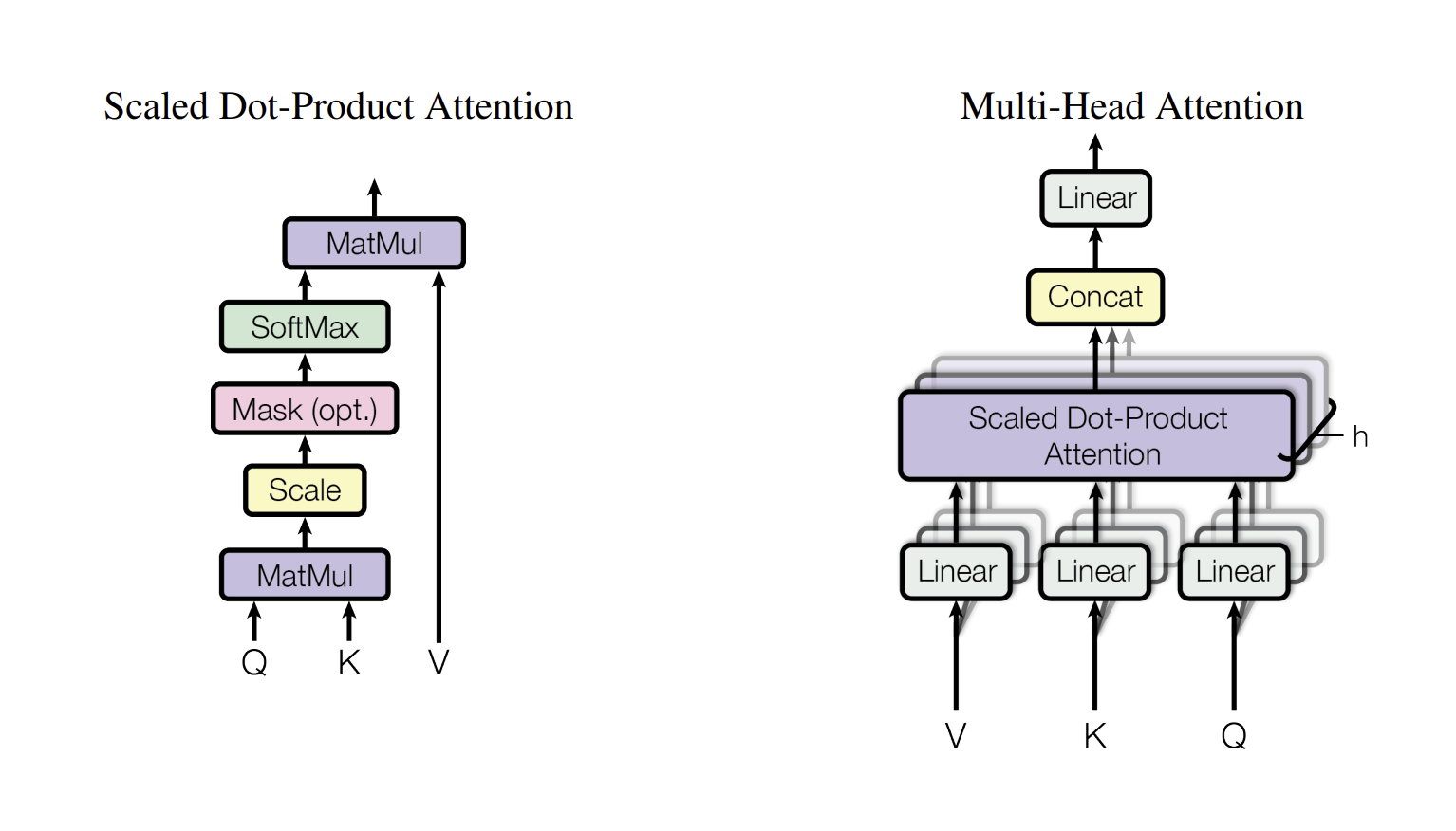
3.2.1 Scaled Dot - Product Attention

위 논문에서 사용하는 attention 이름은 Scaled Dot - Product Attention으로 셀프 어텐션의 내용이 기반으로 되어야 한다.

셀프 어텐션이란?

기존의 논문에서는 encoder와 decoder 의 중요 단어 관계를 attention을 통해 파악했지만, self - attention은 순수하게 encoder에 들어간 단어들끼리, decoder에 들어간 단어들끼리의 관계도를 파악하는 것이다.

예를 들어, A dog ate the food because it was hungry 라는 문장이 있을 때, 여기서 it은 food 가 아닌 dog를 의미하는 것을 알 수 있다. 이와 같이 한 문장(self)에서 각 단어와의 관계도를 표현(attention)해주는 과정이 self-attention이다!

준비 과정

예를 들어 ’I am good’ 이라는 문장이 있다고 가정하면, 이 문장을 기준으로 각 단어의 임베딩을 추출한다.

단어 ‘I’에 대한 임베딩 $x_{1} = [1.76, 2.22, \ldots , 6.66]$
단어 ‘am’에 대한 임베딩 $x_{2} = [7.77, 0.631, \ldots , 5.35]$
단어 ‘good’에 대한 임베딩 $x_{3} = [11.44, 10.10, \ldots , 3.33]$

각 단어에서 추출한 임베딩을 합쳐 임베딩 행렬을 만든다.

\underbrace{ \begin{vmatrix} 1.76 & 2.22 & \ldots & 6.66 \\ 7.77 & 0.631 & \ldots & 5.35 \\ 11.44 & 10.10 & \ldots & 3.33 \\ \end{vmatrix} }_{\text{3x512 행렬}}

위 논문에서의 차원은 512로 임베딩 행렬은 이와 같다. 그리하여 위 논문에서 Query, Key, Value에 대한 행렬 $W^Q ,W^K, W^V$ 를 만든다. 각 행렬의 값은 임의의 값을 가지며, 이후 학습 과정에서 최적화를 이루게 된다.

이후 위의 행렬에서 각각의 $W^Q, W^K, W^V$ 를 곱하여 쿼리 행렬, 키 행렬, 밸류 행렬을 만들게 된다.

\underbrace{ \begin{vmatrix} 3.69 & 7.42 & \ldots & 4.44 \\ 11.11 & 7.07 & \ldots & 76.7 \\ 99.3 & 38.21 & \ldots & 3.98 \\ \end{vmatrix} }_{\text{Query 행렬}}\underbrace{ \begin{vmatrix} 5.31 & 6.78 & \ldots & 0.96 \\ 11.71 & 0.86 & \ldots & 11.31 \\ 10.10 & 11.44 & \ldots & 5.11 \\ \end{vmatrix} }_{\text{Key 행렬}}\underbrace{ \begin{vmatrix} 67.85 & 91.2 & \ldots & 0.13 \\ 13.13 & 63.1 & \ldots & 4.44 \\ 12.12 & 96.1 & \ldots & 43.4 \\ \end{vmatrix} }_{\text{Value 행렬}}

쿼리, 키, 밸류의 첫 번째 행은 단어 “I” 에 대한 쿼리, 키, 밸류 벡터를 의미한다.
쿼리, 키, 밸류의 두 번째 행은 단어 “am” 에 대한 쿼리, 키, 밸류 벡터를 의미한다.
쿼리, 키, 밸류의 세 번째 행은 단어 “good” 에 대한 쿼리, 키, 밸류 벡터를 의미한다.

계산 과정

1단계 : 쿼리와 키 행렬을 곱해준다.

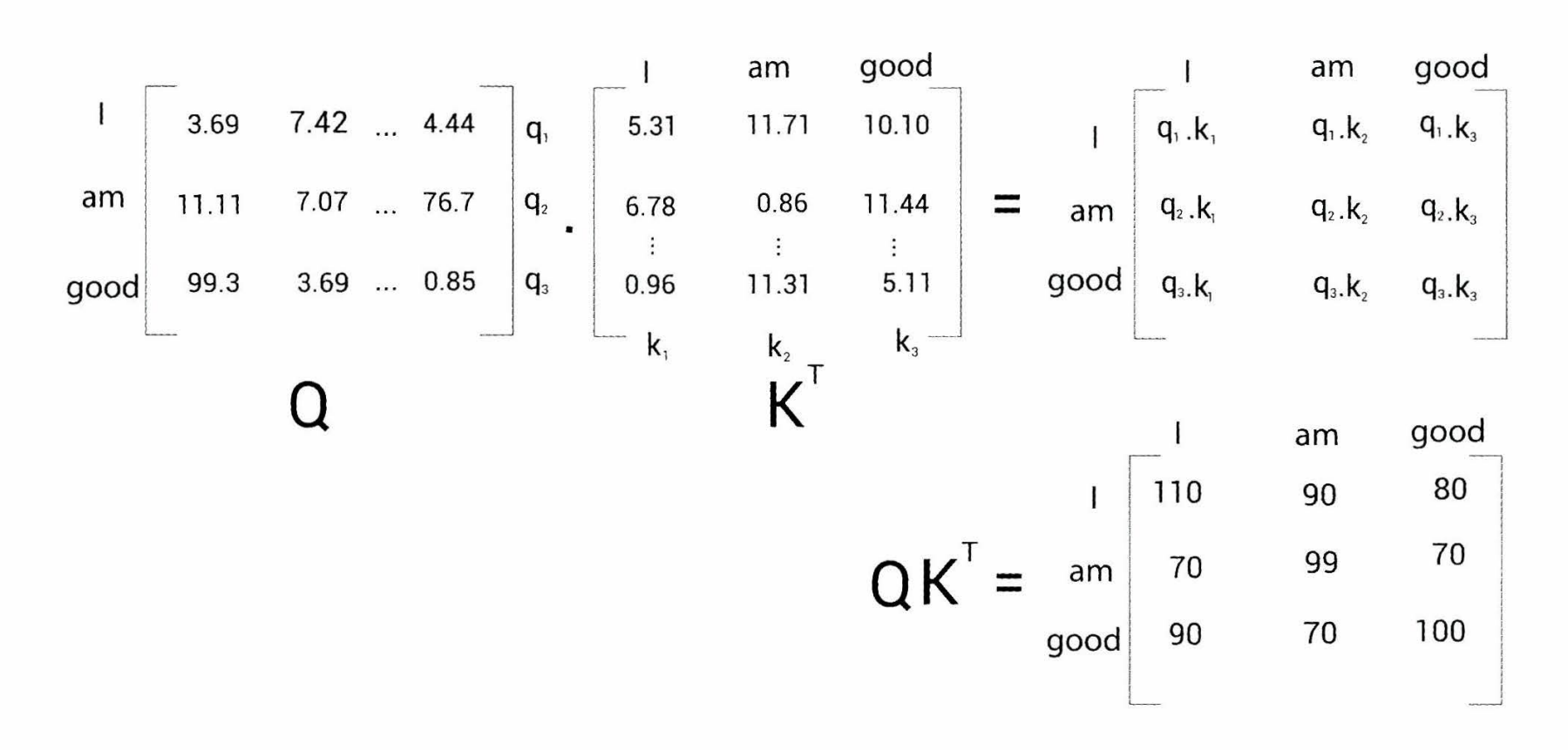
쿼리와 키 행렬를 곱해주면, 각 벡터에 대한 내적으로 행렬이 구성이 됩니다(내적은 두 벡터가 얼마나 유사한지를 알려주는 값으로, 크면 클수록 유사한 것임). 그렇기 때문에 $QK^T$ 에서 1행에서는 ‘I’가 제일 연관성이 높고, 3행에서도 굉장히 연관성이 높은 것으로 보입니다.

2단계 : $QK^T$ 행렬의 키 벡터 차원의 제곱근 값으로 나누어준다.

이 과정을 하는 이유는, 3단계에서 softmax 함수를 줘야하는데 너무 큰 수나 너무 작은 수가 있다면, 이 확률에 대한 값의 차이가 너무 심해져서 제곱근 값으로 나누어주게 됩니다.(Scaling)

3단계 : 이후 확률모델에 대입하기 위해서 유사도 값을 softmax를 이용하여 이의 확률분포를 만든다.

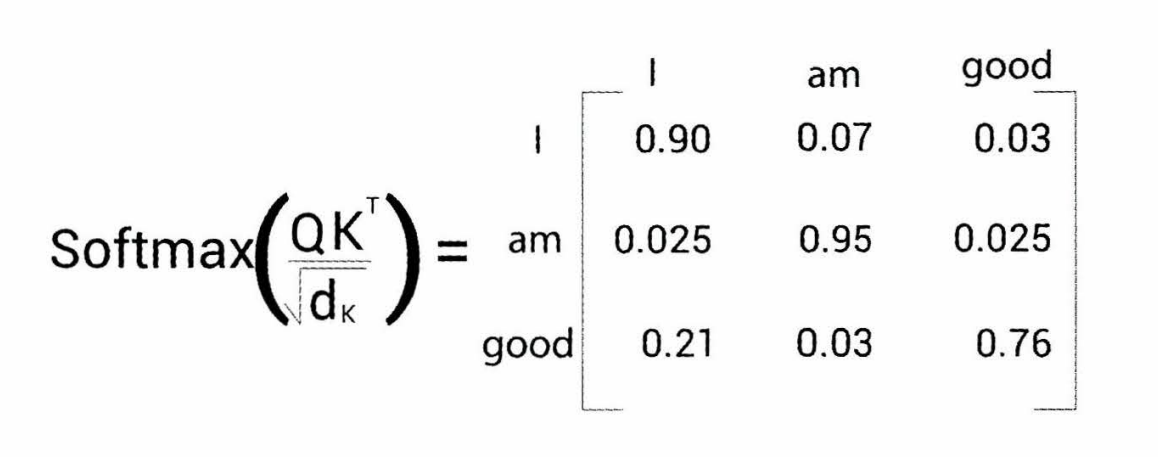
이렇게 되면, 각 단어가 얼마나 다른 단어와 유사한지, 중요한지를 알 수 있게 된다.

4단계 : 이후 밸류 행렬과 곱하여 어텐션 행렬(Z)를 구하게 된다.

<단계별 정리>

1단계 : 쿼리 행렬과 키 행렬 간의 내적을 계산하고 유사도를 산출

2단계 : $QK^T$ 를 키 행렬 차원의 제곱근으로 나눈다

3단계 : 스코어 행렬에 소프트맥스를 적용하여 확률분포를 도출

4단계 : 마지막에 밸류 행렬을 곱하여 어텐션 행렬 $Z$ 도출.

3.2.2 Multi - Head - Attention

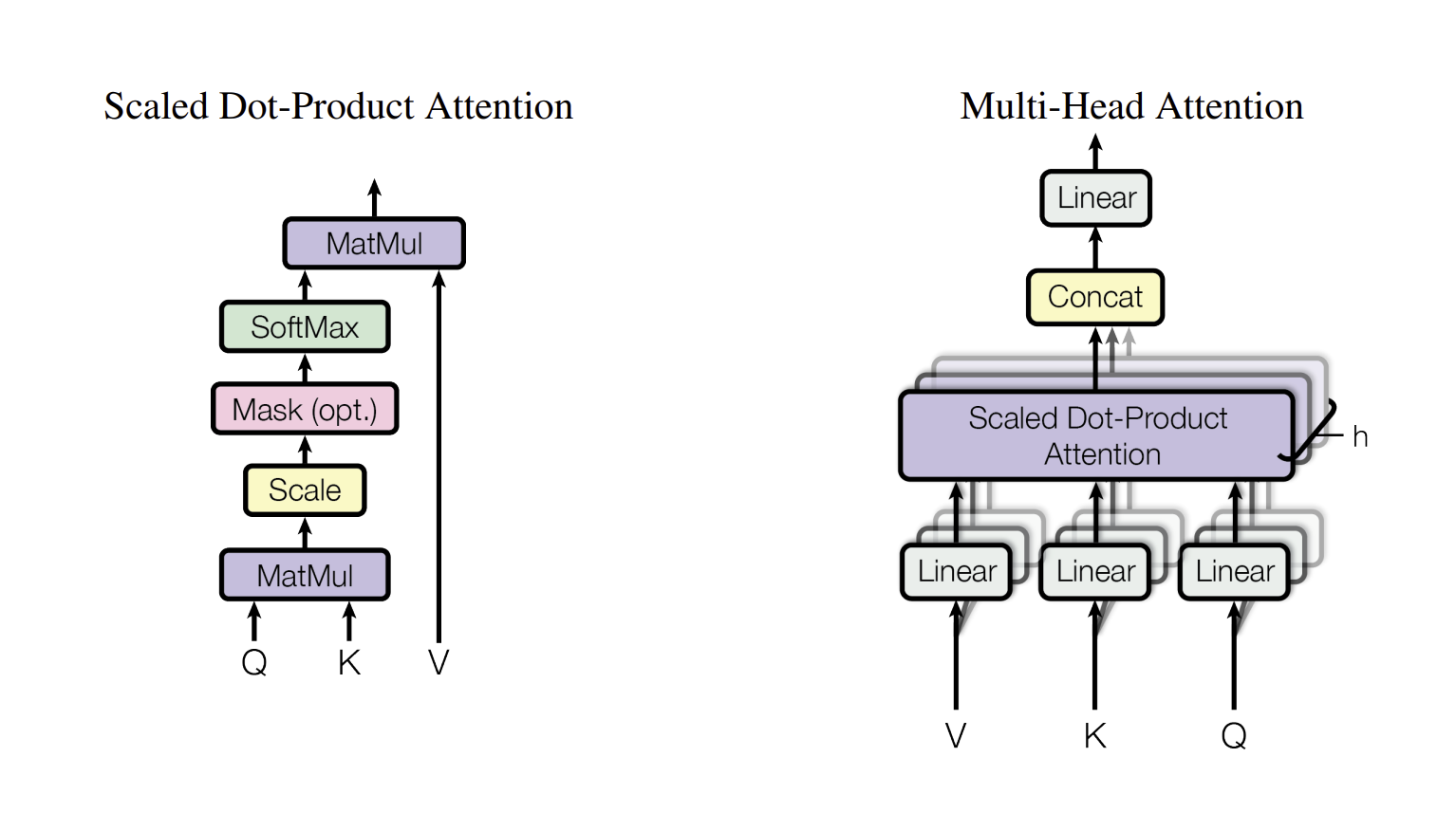
위 그림을 보게 되면, Scaled Dot - Product Attention이 여러 번 등장하는 것을 알 수 있다. Multi(여러 번) 진행했다는 것을 의미한다.

그럼 도대체 왜 여러번 하였을까? 가중치 행렬이 학습을 하면서 최적화가 되겠지만, 내적 값이 항상 유사한 방향으로만 가는 것은 아니다. 그렇기에 어텐션 행렬 $Z$ 즉, head를 여러게 만들어서 그 결괏값을 다 더하는 형태로 진행한다. 이러면 좀 더 정확하게 문장의 의미를 이해할 수 있게 된다. 예를 들어, 한 head는 문장 타입에 집중하는 어텐션을 줄 수도 있고, 명사에 집중하거나 동사에 집중하는 어텐션 등 다양한 어텐션을 더하여 계산을 하게 되는 것이다.

MultiHead(Q, K, V) = Concat(head_{1}, \ldots, head_{h})W^Q\\ where\ head_{i} = Attention(QW_{i}^Q , KW_{i}^K, VW_{i}^V)

3.2.3 Applications of Attention in our Model

위 논문에서는 Attention을 3가지 방법을 사용한다.

encoder-decoder attention
- 위 그림에서 오른쪽 Decoder에 있으며, Decoder의 query와 Encoder의 key와 values를 받아오는 attention
encoder contains self attention layers
- 위 그림에서 왼쪽 Encoder 에 위치한 Multi-Head-Attention
self-attention layer in decoder
- 오른쪽 Decoder 가장 아랫 부분에 위치해있으며, encoder-decoder attention과 다르게 output embedding으로부터 Q(Query), K(Key), V(Value) 모두를 받는다.
- 위에서도 언급했듯이, 미래의 timestep 데이터에 attention이 들어가는 것을 방지하기 위해, 미래의 데이터를 masking을 하였고, 이러한 특성 때문에 Masked Multi-Head-Attention이라고 한다.

3.2.4 쿼리, 키, 밸류 조금 더 이해하기

이는 ‘트랜스포머를 활용한 자연어처리’ 책에서 본 내용을 참고하여 작성하였습니다.

저녁 식사에 필요한 재료를 사러 마트에 갔다고 상상해보죠. 필요한 식재료를 각각 쿼리로 생각하겠습니다. 마트 진열대에 붙은 이름표(키)를 훑으면서 필요한 재료와 일치(유사도 함수)하는지를 확인합니다. 이름표가 일치하면 진열대에서 상품(value)를 꺼내게 됩니다.

이 비유에서는 이름표가 재료와 일치하는 식료품 중 하나만 선택합니다. 즉, 내가 필요한 식재료와 비슷한 이름표를 찾아 구매하고, value 값을 통해 이를 사용하게 되는 것.

즉, 쿼리 = 내가 필요로 생각하는 것, 키 = 필요로 생각하는 것과 비슷한 것, 밸류 = 실제 그 상품

그래서 쿼리와 키를 내적하여 유사도를 측정하고, 실제 확률값을 사용하기 위해 밸류를 곱하여 사용하는 것입니다!

3.3 Position - wise Feed - Forward Networks.

Multi head attention을 데이터가 지난 이후, Feed-forward network를 통해서 신경망 학습을 진행해준다.

FFN(x) = max(0, xW_{1} + b_{1})W_{2} + b_{2}

3.4 Embedding and Softmax

Encoder와 Decoder에는 각각 Embedding block이 존재하고, 모두 똑같은 차원의 수로 시퀀스를 만들어준다. 그리고 디코더 부분에서 linear transformation을 지나고 이를 확률로 변환해주기 위해 softmax 함수를 사용해준다. 각 embedding layer와 linear transformation에는 똑같은 가중치를 사용해준다.

3.5 Positional Encoding

기존의 RNN과 LSTM과는 다르게 시퀀스 데이터를 학습할 때, 순서를 고려하지 않고 병렬로 데이터를 한번에 처리하기 때문에 순서를 고려할 수 없게 됩니다. Multi-head-attention에 데이터를 그냥 넣게 되면, 단어의 순서 차이 없이 학습을 하게 된다.

따라서 단어의 위치 정보를 제공해줘야 한다. 그래서 위 논문은 “Positional Encoding” 을 넣어 이를 고려해준다. 모델의 기본 차원인 512 차원과 같게 맞추어주고 계산을 한다.

PE(pos,2i) = sin(pos/10000^{2i/d_{model}})\\ PE(pos, 2i+1) = cos(pos/10000^{2i/d_{model}}),\\ where\ pos = position, i = demension

그리하여 Input_data는 512 차원으로 항상 같은 문장의 위치 값이 포함된 $PE$ 를 더하여Multi_head_attention에 넣게 됩니다.

Input data의 성질

n개의 단어 각각 임베딩을 하고 모으게 되면 n x 512 차원의 행렬이 만들어진다.
하지만 m개의 단어가 들어오는 경우에는 $max(n,m)$ 을 맞춰서 padding 작업을 통해서 맞춰줘야 한다.

Cos과 Sin의 활용

위 논문에서는 $\cos(x)$ 과 $\sin(x)$ 함수를 통하여 PE를 계산합니다. 그렇다면 도대체 왜 $\cos, \sin$ 을 사용할까요?

먼저 input_data를 표현하는 방법에는 굉장히 많은 방법이 있습니다.

단어 시퀀스 순서마다 indexing 해주기.

a = [0,1,2,3,4,5,6,7,8,\cdots]

이 방법은 데이터의 값이 너무 커지기에 학습시 문제(Gradient Exploding)을 겪을 수 있습니다.

Normalize Indexing

a = [0, 0.02, 0.03,0.06,0.08,0.11,\cdots, 1]

이 방법은 길이가 너무 가변적이고, max_length가 다른 데이터셋에 대해서는 비교가 불가능하기에 사용할 수 없습니다.

그래서 트랜스포머의 Positional Encoding(sinusoidal positional encoding)의 전제는

모든 위치값은 시퀀스의 길이나 input에 관계없이 동일한 식별자를 가져야 한다. 즉 input data가 바뀌어도 각 단어별로 더하게 될 PE 값은 같아야 됩니다.

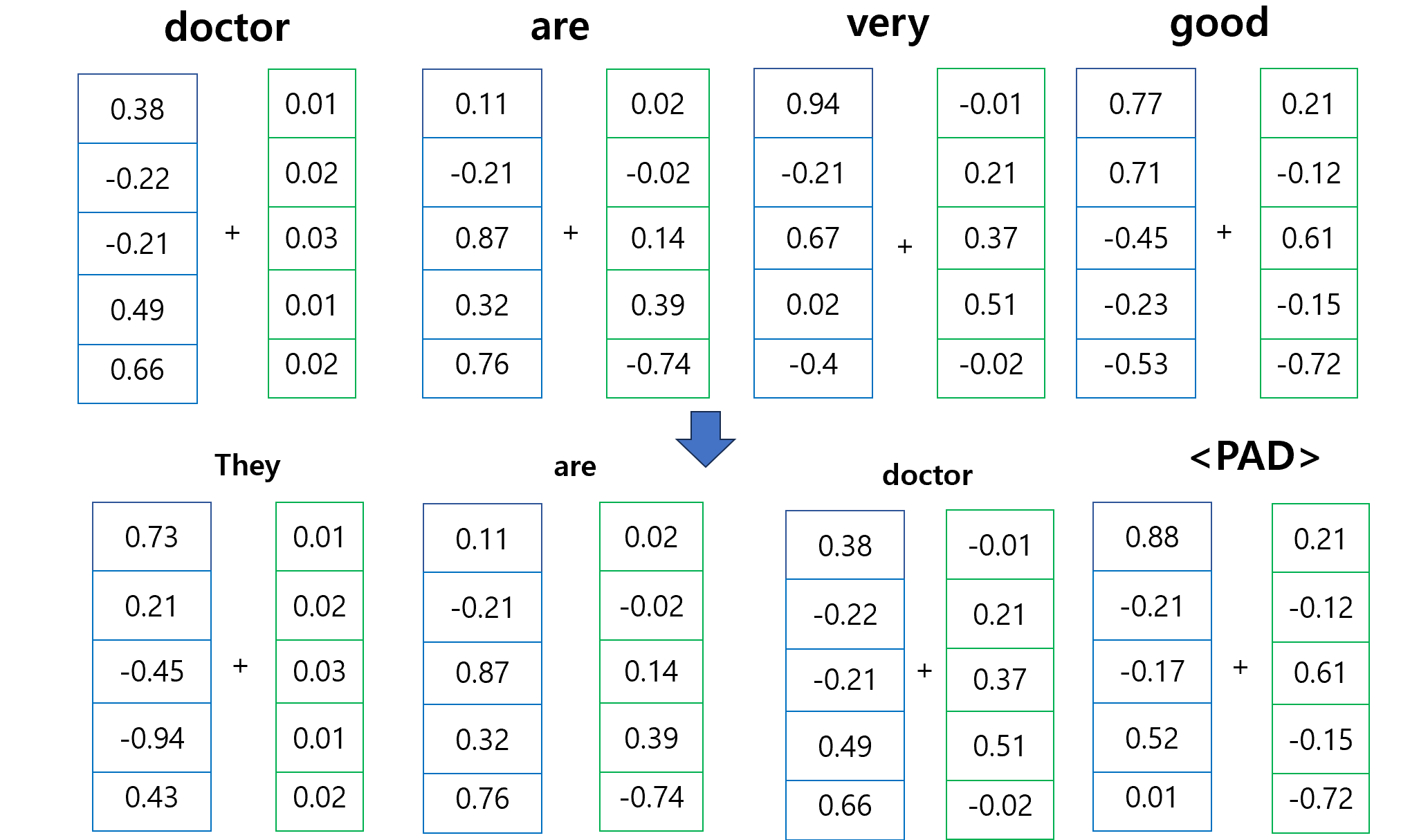
다음 그림과 같이 임베딩 벡터의 차원은 5이고, 각 PE가 더해질 때는 순서에 마다 다 똑같은 값을 더해주어야 합니다. 단어를 임베딩 벡터로 하면 각자 다 다름 + 똑같은 순서에 해당하는 값마다 다 더해주기 때문에 단어의 순서 차이가 나게 됩니다. 예를 들어, 위 문장에서 doctor는 임베딩 벡터는 같지만, 순서가 다르기 때문에 각각 다른 PE가 더해집니다. 이는 결국 다른 값들을 의미하며, 다른 순서를 가진다고 해석할 수 있습니다.

그리고 PE 첫번째 벡터의 값은 너무 크면 안됩니다.

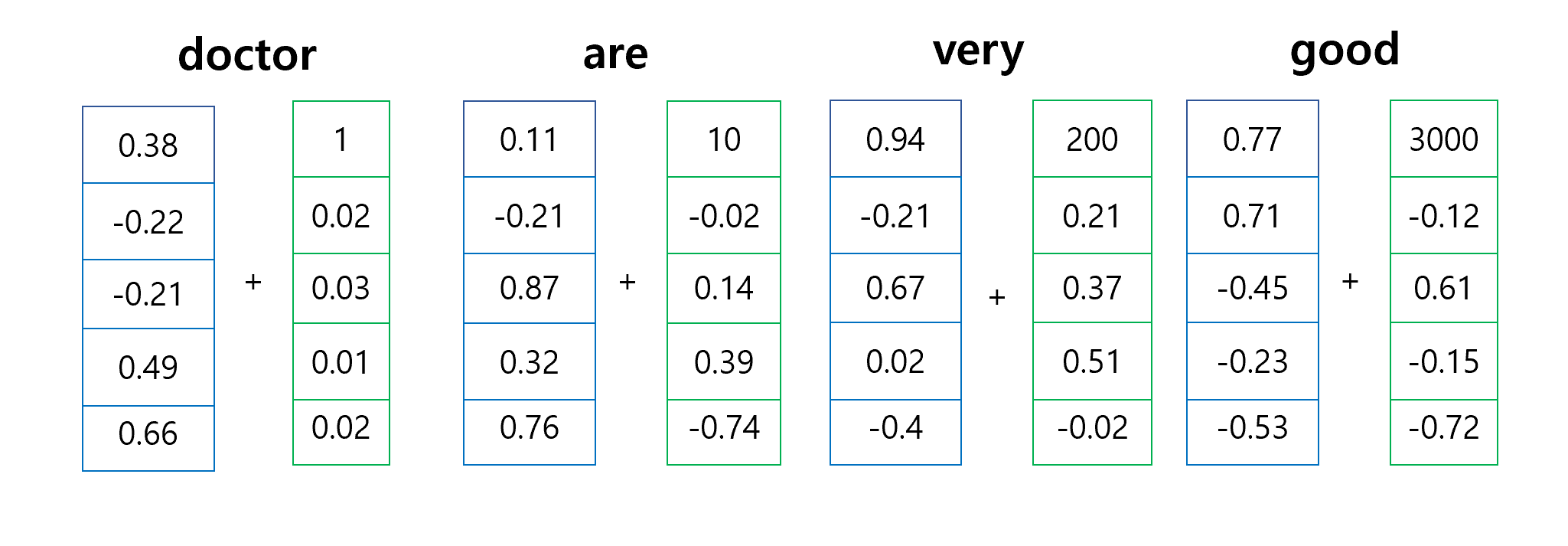
이는 여러 문제( ex → 기울기 소실, 학습속도 저하) 등의 문제를 일으킬 수 있습니다.

그리하여 위와 같은 문제를 해결하기 위해서는 아무리 무한대로 갈 정도로 값이 커도 치역을 -1과 1 사이로 제한시켜 줄 수 있고, 위치 벡터들의 차이가 많이 크지 않는 값으로 변환 해주는 $\sin(x)$ 과 $\cos(x)$ 을 사용하는 것입니다. 아무리 다른 PE지만 같은 값이 나오더라도 이는 다차원의 벡터 값이기에 거의 같아질 일은 없습니다..

Sinusoidal Encoding

이제 $\sin(x)$ 과 $\cos(x)$ 사용하는 이유를 알았다면, $\sin, \cos$ 안에 $pos/10000^{2i/d_{model}}$ 값을 합성하는 이유를 알아봅시다.

핵심은 $i$ 를 대입하면 알 수 있습니다. 만약 $i$ 값이 커진다면, 합성함수를 해석해보았을 때, 합성함수의 정의역이 작아지면서 삼각함수의 그래프가 매우 늘어지는 그래프가 됩니다. 이는 정의역이 $\Delta x$ 만큼 움직인다면, y값의 변화는 거의 없기에 PE 값이 잘 변하지 않게 됩니다. 즉 문장의 넓은 범위에 걸친 관계를 인코딩할 수 있다는 것을 의미합니다.

더 자세한 내용은 아래 영상을 참고하면 좋겠습니다.

Positional embeddings in transformers EXPLAINED | Demystifying positional encodings.

4. Why Self Attention?

위 논문에서는 Self Attention이 RNN과 같은 recurrent network를 비교하기 위해 다양한 관점에서 이를 설명하고 있습니다.

전체적인 계산 복잡도.
병렬화할 수 있는 양
long-range dependencies 사이의 문장의 길이
1. 문장이 짧으면 짧을수록 학습을 잘하기에, 각 모델을 max_length을 이용하여 성능 비교

결과적으로, RNN계열 아키텍처가 $O(n)$ 의 sequential operation을 필요로 하지만, self-attention layer는 상수 번 $O(1)$ 의 sequential operation만 진행하면 되었다. 즉, self-attention layer가 더 많이 병렬화 작업을 수행할 수 있고, 이를 통해 학습 시간을 현저히 줄일 수 있다는 것이다.
또한, 계산 복잡도 측면(computational complexity)에서는, self-attention layer는 $n$ (sequence length)이 $d$ (representation dimensionality) 보다 작을 때 RNN 계열의 아키텍처보다 더 적은 계산 복잡도를 가지는 것을 알 수 있다.
Maximum path length 측면에서도 self-attention이 가장 작은 Maximum path length을 가지는 것을 확인할 수 있다. 이를 통해 self-attention 기반 모델은 Long-range dependencies를 더 쉽게 학습할 수 있다.

5. Training

5.3 Optimizer

논문에서 optimizer는 $Adam$ 을 사용하였고, 이에 대한 $Hyper \ parameters$ 값은 $\beta_{1} = 0.9, \beta_{2} = 0.98 \ and \ \epsilon = 10^{-9}$ 이다.

5.4 Regularization

Residual Dropout : $P_{drop} = 0.1$ 로 dropout 비율을 설정하여 학습을 하였다.

Label Smoothing : 학습을 하는 동안, smoothing value를 설정하여 BLEU와 accuracy를 높였다.

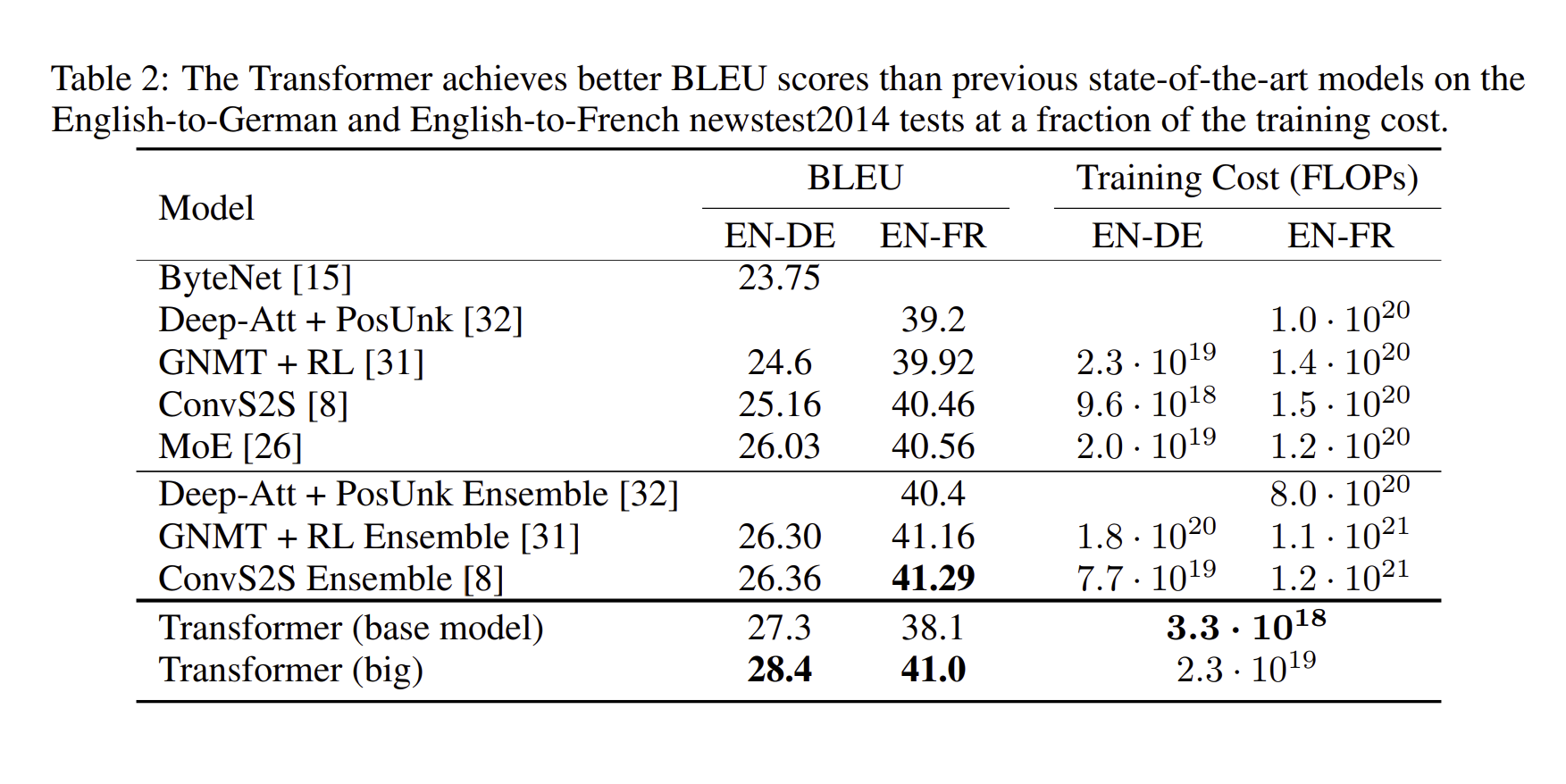
위의 표 결과, 그 당시 나왔던 모델들 중에서 가장 높은 BLUE 값을 받았으며, training 시간도 매우 적었음(무려 $10^{18}$ … )을 알 수 있다.

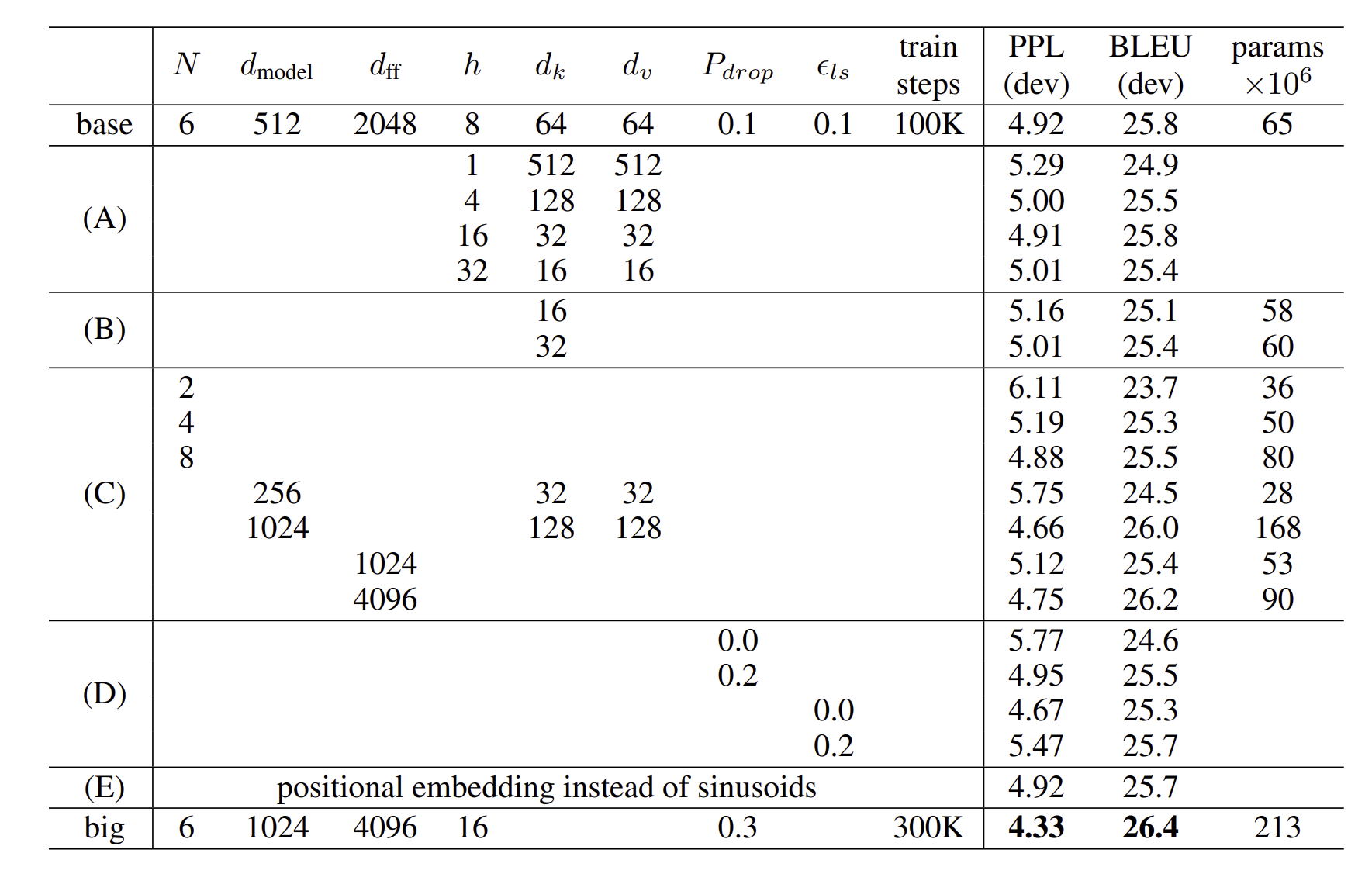
이는 하이퍼 파라미터 값을 조정하면서 학습을 하였는데, 결과는 다음과 같다.

(B) : Attention의 key 사이즈를 줄이면 model quality가 줄어든다는 점.

(E) : sinusoidal Positional Encoding에서 learned positional embeddings로 바꾸었더니 성능이 비슷했다는 점.

요약 - 한 줄로 정리를 하자면?

Transformer는 Encoder와 Decoder로 구성된 모델로, Positional Encoding으로 병렬 처리와 위치 정보를 동시에 진행하면서, 한 문장에 어느 단어가 서로 유사한 지를 직접 계산하며 학습하는 모델이다. (Self Attention) → 대단…

후기

트랜스포머 논문을 2022년 여름쯤에 처음 들어봤는데 제대로 공부해본 것은 이번이 처음이라.. 굉장히 어렵습니다.. ㅠ 수학적 수식만을 본다기 보다는, 실제로 함수 자체가 왜 사용 되었는지를 포커스 맞추면서 나가야 전체적인 구조가 이해가 가네요! 한 3~4번 정도는 더 봐야 이해하지 않을까 싶습니다!!

참고

찬호

그냥 끄적여 보는 논문..

이전 포스트

[논문 리뷰] Neural Machine Translation by Jointly Learning to Align and Translate - Bahdanau Attention

다음 포스트