알고리즘 무한 연습!
정글 커리큘럼에서 쉬운 건 풀었음.
아직 입력 값 처리에서 실수가 많고, 기초적인 문법이 약한 것 같아서 백준 카테고리 별로 기본적인 문제부터 풀어보면서 문제 익숙해져야겠음.
벨로그에는 기억해야 할만한 풀이만 기록
투 포인터로 풀면 편하다!
반복문 돌릴 때 i쓰는 것보다 투 포인터로 풀면 편함.
백준 10811 (바구니 뒤집기)
N, M = map(int, input().strip().split())
orders = [input().strip() for _ in range(M)] # 문자로 "1 2"처럼 저장됨
buckets = [str(i) for i in range(1, N + 1)]
for order in orders:
codes = order.split()
left_pointer = int(codes[0]) - 1 # 인덱스로 변환
right_pointer = int(codes[1]) - 1
while left_pointer < right_pointer:
buckets[left_pointer], buckets[right_pointer] = buckets[right_pointer], buckets[left_pointer]
left_pointer += 1
right_pointer -= 1
print(" ".join(buckets))오류 복기
아무 생각 없이strip().split()을 쓰는 경우 많음
상황에 따라서 생각하면서 코딩하기
try-except로 입력받기
백준 11718 (그대로 출력하기)
words = []
while True:
try:
word = input()
words.append(word)
except:
break
for word in words:
print(word)문제는 쉬운데 횟수가 정해지지 않는 입력받는 것 몰랐음
try-except으로 입력받는 것 기억하기
" ".join(arr)
join()은 str 자료형끼리만 가능하다.
리스트의 원소가 int인 경우에는 결합이 불가능!
백준 3003 (킹, 퀸, 룩, 비숍, 나이프, 폰)
pieces = list(map(int, input().strip().split()))
answer = [1, 1, 2, 2, 2, 8]
result = []
for i in range(6):
count = answer[i] - pieces[i]
result.append(count)
result = list(map(str, result))
print(" ".join(result))range() 역순 정리
# 시작부터 0 직전까지 -1씩 생성
# range(start, end, step)에서 start는 포함되지만 end는 포함되지 않음.
range(5, 0, -1) # [5, 4, 3, 2, 1]step이 양수이면
start < end인 경우만 생성됨.
step이 음수이면start > end인 경우만 생성됨.
1주차 알고리즘 시험
3개 중에 1개 풀었음.
1번 문제에서 88%에서 계속 시간 초과 발생.
문자 형태의 숫자가 0이 있고 없고를 체크하지 않아서 생기는 문제.
1번 문제 쉬운 건데 40분 걸림.
백준 1110 (더하기 사이클) 최초 풀이
N = input() # 문자로 저장
digit_N = N
cnt = 0
while True:
# pad로 코드 줄일 수 있을 것 같은데 기억 안남.
if len(digit_N) == 1:
digit_N = "0" + digit_N
a = digit_N[0]
b = digit_N[1]
temp_sum = str(int(a) + int(b))
new_N = b + temp_sum[-1] # new_N은 숫자형태의 문자열
cnt += 1
# 사이클 일치하는지 비교
if int(N) == int(new_N):
print(cnt)
break
else:
digit_N = new_N파이썬에서 빈 곳 채우는 코드
zfill(n)(0을 넣어서 자릿수를 맞춤)
zfill() 예시
# 양수
origin_string = "42"
formatted_string = original_string.zfill(5)
print(formatted_string) # 출력: "00042"
# 음수
negarive_string = "-7"
formatted_negative_string = negative_string.zfill(5)
print(formatted_negative_string) # 출력: "-0007"백준 1110 (더하기 사이클) 코드 리뷰 개선 풀이
N = int(input())
now_number = N
cnt = 0
while True:
a = now_number // 10
b = now_number % 10
digit_sum = a + b
first_number = b * 10
last_number = digit_sum % 10
new_number = first_number + last_number
cnt += 1
if new_number == N:
print(cnt)
break
else:
now_number = new_number스트링으로 구하는 것보다 숫자로 구하는 게 훨씬 깔끔함!
조합 구하는 것 hands on
1. combination 모듈 사용
from itertools import combinations
def get_combination(iterable, r):
# combinations는 순환 가능한 combinations 객체를 반환
return list(combinations(iterable, r))
my_list = [1, 2, 3, 4]
combos = get_combination(my_list, 2)
for combo in combos:
print(combo)
2. 재귀로 조합 구하기
# 보류백준 1182 부분 수열의 합
from itertools import combinations
N, S = map(int, input().strip().split())
arr = [int(n) for n in input().strip().split()]
combos = []
cnt = 0
for i in range(1, N + 1):
combo_i = list(combinations(arr, i))
for combo in combo_i:
combos.append(combo)
for combo in combos:
if sum(combo) == S:
cnt += 1
print(cnt)오류 복기
combinations를combination으로 s 빼먹음.
append()에 파라미터 안 넘김
sum(combo)를 sum(combos)로 전체 리스트를 넘김.
새로운 발제
주요 주제: 그래프
트리 탐색
인접행렬?
다익스트라
MST(최소 신장 트리)
코치진 면담
(원장님)
스스로 문제를 해결할 수 있는지 본다.
요즘 문제가 '안 배웠는데요'하는 것(머리 절레절레 하심)
'안 배웠는데요'하는 게 아니라 스스로 습득할 수 있는 사람을 선호.
기술을 보는 게 아니라 태도를 본다.
'모르겠습니다' 안 좋다.
(원장님, 김코치님)
포트폴리오 결과물이 중요한 게 아니다.
그 과정에서 어떤 문제를 해결했는지, 그런 스토리가 중요
(백코치님)
OS 다뤘다고 하는데 면접에서 기본 개념도 제대로 대답 못하면 탈락
개념을 훑고 지나가지 말고 집요하게 파고 들어라.
정수론
(키워드에 있었는데 못 봄)
코드 리뷰 소감
처음으로 코드 리뷰 해봄.
(내가 못 푼 문제를 리뷰하는 게 맞나 싶지만..)
타인이 쓴 코드를 보면서 가독성 높은 코드를 고민하게 되었음!
코드 리뷰가 다른 사람의 코드를 개선해 주는 과정이라기보다
타인의 코드를 보면서 가독성 높은 코드가 무엇인지 생각해 보는 계기가 됨!
2주차 키워드
그래프
vertex
edge
node
arc
BFS
DFS
위상정렬
그래프
vertex와 edge로 구성된 한정된 자료 구조
수학적 정의: 객체의 일부 쌍들이 '연관되어' 있는 객체 집합 구조
vertex(꼭지점): node라고 볼 수 있음. 정확히 그래프의 node를 vertex라고 함.
edge: 정점을 연결하는 간선(무방향성 연결선)
arc: 정점을 연결하는 간선(방향성 연결선, 방향을 나타내는 기호를 사용)
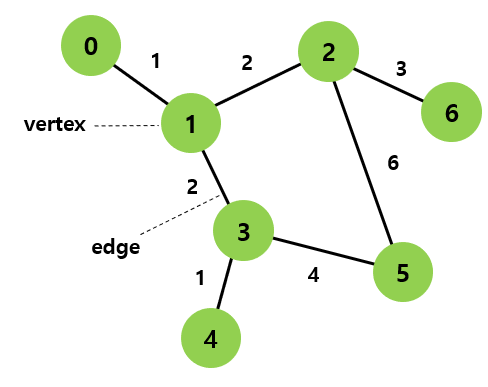
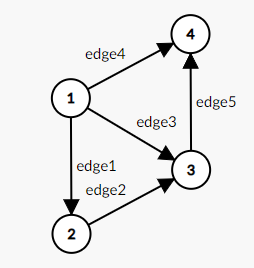
그래프를 표현하는 방법
1. 인접 행렬
2. 인접 리스트
무방향성 그래프의 간선은 edge
방향성 그래프의 간선은 arc
오일러: "모든 정점이 짝수 개의 차수를 갖는다면 모든 다리를 한 번씩만 건너서 도달하는 것이 성립한다."
트리
각 노드가 m개 이하의 자식을 갖고 있으면 m-ary(에리)트리라고 한다.
트리의 정의 기억하자!
용어 정리
1. 루트(root): 트리의 가장 위에 있는 노드
2. 리프(leaf): 가장 아래쪽에 있는 노드
단말 노드(terminal node), 외부 노드 (external node)라고도 함.
(terminal: 종료 지점을 나타내는 용어)
3. 비단말 노드(non-terminal node): 리프를 제외한 노드
내부 노드(internal node)라고도 함.
3. 자식(child): 어떤 노드의 아래쪽 노드
4. 부모(parent): 어떤 노드의 위쪽 노드
5. 형제(sibling): 부모가 같은 노드
6. 조상(ancestor): 노드에서 위쪽으로 따라가서 만나는 모든 노드
7. 자손(descendant): 노드에서 아래쪽으로 따라가서 만나는 모든 노드
8. 레벨(level): 루트에서 얼마나 멀리 떨어져 있는지(루트는 0 레벨)
9. 차수(degree): 각 노드가 갖는 자식의 수
(모든 노드 차수가 n이하인 트리를 n진 트리라고 함.)
10. 높이: 루트에서 가장 멀리 있는 리프까지 거리(리프 레벨의 최대값)
11. 서브트리(subtree): 특정 노드를 루트로 하는 트리
12. 빈 트리(none tree, null tree): d노드와 가지가 전혀 없는 트리
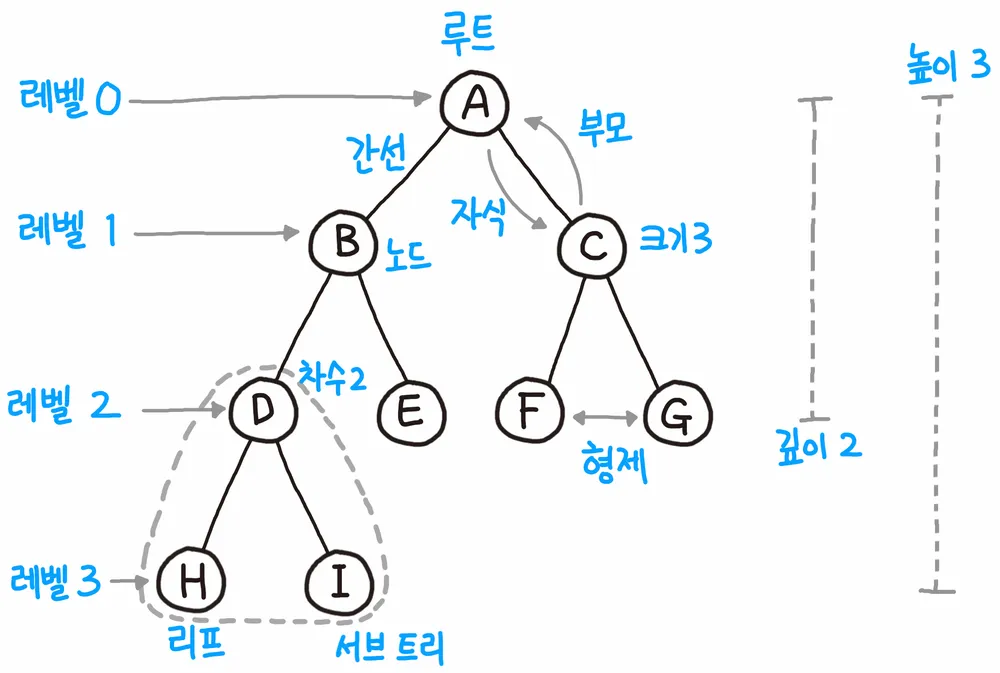
순서 트리 vs 무순서 트리
순서 트리(ordered tree): 형제 노드에 순서 관계가 있음
ex) 문서의 제목과 하위 구조, 디렉터리 구조(순서가 있어야 검색 용이)
무순서 트리(unordered tree): 형제 노드에 순서 관계가 없음(부모 자식 관계만 중요)
ex) 조직도
트리 vs 그래프
트리는 순환 구조(Cycle)를 갖지 않는 그래프이다.
트리는 특수한 형태의 그래프의 일종이다.
그래프의 범주에 속한다.
그래프는 단방향(Uni-Directional), 양방향(Bi-Direvtional)을 모두 가리킬 수 있다.
트리는 부모 노드에서 자식 노드를 가리키는 단항뱡 뿐이다.
트리는 하나의 부모 노드를 갖는다.
트리는 루트 노드가 하나이다.
궁금한 점: 트리에 자식 노드가 3개일 수도 있을까?
있다! 자식이 2개인 트리는 이진 트리(Binary Tree)이며, 가장 흔한 구조
트리의 정이에는 자식 노드의 수에 대한 제한이 없다.
다진 트리(다항 트리)(Multiway Tree) 또는 n분 트리(n-ary Tree)도 가능
이진 트리(Binary Tree)
모든 노드의 차수(m)이 2 이하일 때를 특별히 이진 트리라고 함.
이진 트리의 종류
1. 정 이진 트리(Full Binary Tree): 모든 노드가 0개 또는 2개의 자식 노드
2. 완전 이진 트리(Complete Binary Tree):
마지막 레벨을 제외하고 모든 레벨이 완전히 채워져 있다
마지막 레벨은 왼쪽부터 채워져 있다.
(heap 구현에 용이)
3. 포화 이진 트리(Perfect Binary Tree)
모든 노드가 2개의 자식 노드
모든 리프 노드가 동일한 깊이 또는 레벨
(가장 완벽한 유형의 트리)
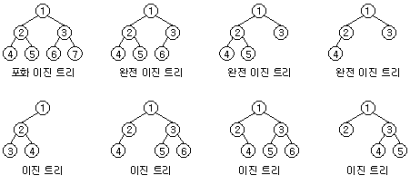
노드의 깊이와 레벨은 뭐가 다르지?
깊이: 루트 노드로부터 특정 노드까지의 경로의 길이(루트 노드 깊이는 0)
레벨: 트리의 각 층을 나타내는 개념(루트는 레벨 0)
tree hands on
그대로 따라치지 않고 GPT 활용해서 직접 클래스로 구현해 봄!
class Node:
# 단일 책임 원칙(클래스는 하나의 주요 책임만 가져야 한다.)
def __init__(self, data):
self.data = data
self.left = None
self.right = None
# 개방 폐쇄 원칙(확장에는 열려있고 수정에는 닫혀 있어야 한다.)
# 초기화 프로세스 등 부가적인 작업은 별도 메서드로 분리하여 클래스 역할을 명확하게 한다.
def set_children(self, left_node=None, right_node=None):
self.left = left_node
self.right = right_node
class Tree:
def __init__(self, root):
self.root = root
def set_root(self, node):
self.root = node
def get_root(self):
return self.root
def preorder_traversal(self, node):
if node:
print(node.data, end=" ")
self.preorder_traversal(node.left)
self.preorder_traversal(node.right)
def inorder_traversal(self, node):
if node:
self.inorder_traversal(node.left)
print(node.data, end=" ")
self.inorder_traversal(node.right)
def postorder_traversal(self, node):
if node:
self.postorder_traversal(node.left)
self.postorder_traversal(node.right)
print(node.data, end=" ")
root = Node(1)
root.set_children(Node(2), Node(3))
root.left.set_children(Node(4), Node(5))
tree = Tree(root)
print("전위 순회:")
tree.preorder_traversal(tree.get_root())
print("\n")
print("중위 순회:")
tree.inorder_traversal(tree.get_root())
print("\n")
print("후위 순회:")
tree.postorder_traversal(tree.get_root())
print("\n")
전위 순회:
1 2 4 5 3
중위 순회:
4 2 5 1 3
후위 순회:
4 5 2 3 1
자료 구조를 직접 짜 보는게 자료 구조 이해에 많은 도움이 됨!
그 전까지는 알고리즘 책 보고 그냥 따라서 짰는데
이번에는 (GPT 도움을 받기는 했지만) OPP 원칙 생각하면서 스스로 짜 봄!
자료 구조를 짜 보면서 트리, 재귀, 객체지향에 대해서 공부하게 됐음!
트리 탐색(전위, 중위, 후위)도 이해됨!
이진 탐색 트리(Binary Search Tree(BST))
이진 탐색 트리는 이진 트리의 한 종류임
다음 조건을 충족해야 함
1. 각 노드에 하나의 값이 있음.
2. 값들은 전순서가 있다.
3. 노드의 왼쪽 서브트리에는 그 노드의 값보다 작은 값들을 지닌 노드들로 구성
4. 오드의 오른쪽 서브트리에는 그 노드의 값보다 큰 값들을 지닌 노드들도 구성
이진 탐색 트리는 왼쪽 자식들은 작아야 되고, 오른쪽 자식들은 커야 됨.
BFS(breadth-first search, 너비 우선 탐색)
폭 우선 검색, 가로 검색, 수평 검색(맹목적 탐색 방법의 하나)
DFS보다 쓰임새는 적지만 최단 경로 찾는 다익스트라 알고리즘 등에 유용
- 시작 정점 방문(가까운 노드 탐색)
- 시작 정점에 인접한 모든 정점들을 우선 방문
BFS는 큐(Queue)를 통해 구현된다.(FIFO)
1. 낮은 레벨부터 왼쪽에서 오른쪽으로 검색
2. 한 레벨 검색 마치면 다음 레벨
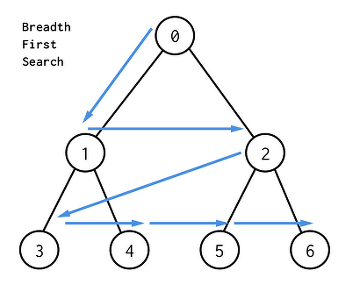
수도 코드
1. 출발점을 큐에 넣고 아래 로직을 반복한다.
1-1. 큐에 저장된 정점을 하나 dequeue한다.
1-2. dequeue된 정점과 연결된 모든 정점을 큐에 넣는다.
1-3. 큐가 비어있으면 반복 종료
BFS의 주요 용도
- 최단 경로 탐색
- 그래프 순회
- 검색 문제: 상태 공간 트리(문제 해결 과정 중 중간 상태의 트리)에서 최적의 상태 찾기
BFS 는 Queue나 linked list로 구현하는 게 일반적
BFS hands on
(BFS는 재귀구조로 구현 불가)
큐를 이용한 반복 구조
graph = {1: [2, 3, 4], 2: [5], 3: [5], 4: [], 5: [6, 7], 6: [], 7: [3]}
def iterative_bfs(start_v):
discovered = [start_v]
queue = [start_v]
print(f"방문 리스트에 시작 노드 ${start_v}를 삽입합니다.")
print(f"큐에 시작 노드 ${start_v}를 삽입합니다.")
while queue:
v = queue.pop(0)
print(f"큐에서 첫 번째 노드 {v}를 pop하고 {v}의 인접 노드를 탐색합니다.")
for w in graph[v]:
if w not in discovered:
discovered.append(w)
queue.append(w)
print(f"방문 리스트에 {w}를 삽입합니다.")
print(f"큐에 {w}를 삽입합니다.")
return discovered
print(iterative_bfs(1))
방문 리스트에 시작 노드 1를 삽입합니다.
큐에 시작 노드 1를 삽입합니다.
큐에서 첫 번째 노드 1를 pop하고 1의 인접 노드를 탐색합니다.
방문 리스트에 2를 삽입합니다.
큐에 2를 삽입합니다.
방문 리스트에 3를 삽입합니다.
큐에 3를 삽입합니다.
방문 리스트에 4를 삽입합니다.
큐에 4를 삽입합니다.
큐에서 첫 번째 노드 2를 pop하고 2의 인접 노드를 탐색합니다.
방문 리스트에 5를 삽입합니다.
큐에 5를 삽입합니다.
큐에서 첫 번째 노드 3를 pop하고 3의 인접 노드를 탐색합니다.
큐에서 첫 번째 노드 4를 pop하고 4의 인접 노드를 탐색합니다.
큐에서 첫 번째 노드 5를 pop하고 5의 인접 노드를 탐색합니다.
방문 리스트에 6를 삽입합니다.
큐에 6를 삽입합니다.
방문 리스트에 7를 삽입합니다.
큐에 7를 삽입합니다.
큐에서 첫 번째 노드 6를 pop하고 6의 인접 노드를 탐색합니다.
큐에서 첫 번째 노드 7를 pop하고 7의 인접 노드를 탐색합니다.
[1, 2, 3, 4, 5, 6, 7]DFS(depth-first search, 깊이 우선 탐색)
세로 검색, 수직 검색
1. 리프에 도달 할 때까지 아래로 내려가면서 검색
2. 내려갈 곳이 없으면 부모 노드로 돌아감
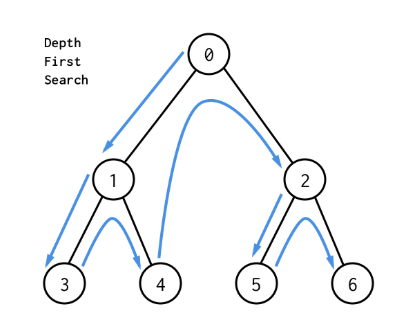
DFS의 스캔 방법
1. 전위 순회(preorder)
노드 방문 -> 왼쪽 자식 -> 오른쪽 자식
2. 중위 순회(inorder)
왼쪽 방문 -> 노드 방문 -> 오른쪽 자식
3. 후위 순회(postorder)
왼쪽 자식 -> 오른쪽 자식 -> 노드 방문
DFS는 한 놈만 패기 때문에(?) 재귀 함수로 구현하는 게 일반적
한 노드에서 어떻게 행동해야하는지만 기술
DFS hands on
재귀로 구현
graph = {1: [2, 3, 4], 2: [5], 3: [5], 4: [], 5: [6, 7], 6: [], 7: [3]}
def recursive_dfs(v, discovered=[]):
discovered.append(v)
print(f"방문한 노드 {v}를 방문 리스트에 추가합니다.")
for w in graph[v]: # 특정 노드에 연결된 노드들을 순회
if w not in discovered:
print(f"{w}노드를 재귀적으로 방문합니다.")
discovered = recursive_dfs(w, discovered)
else:
print(f"{w}는 이미 방문했습니다.")
return discovered # 모든 노드를 방문한 후에 방문한 순서대로 리스트 반환
print(recursive_dfs(1))
방문한 노드 1를 방문 리스트에 추가합니다.
2노드를 재귀적으로 방문합니다.
방문한 노드 2를 방문 리스트에 추가합니다.
5노드를 재귀적으로 방문합니다.
방문한 노드 5를 방문 리스트에 추가합니다.
6노드를 재귀적으로 방문합니다.
방문한 노드 6를 방문 리스트에 추가합니다.
7노드를 재귀적으로 방문합니다.
방문한 노드 7를 방문 리스트에 추가합니다.
3노드를 재귀적으로 방문합니다.
방문한 노드 3를 방문 리스트에 추가합니다.
5는 이미 방문했습니다.
3는 이미 방문했습니다.
4노드를 재귀적으로 방문합니다.
방문한 노드 4를 방문 리스트에 추가합니다.
[1, 2, 5, 6, 7, 3, 4]반복문으로 구현
graph = {1: [2, 3, 4], 2: [5], 3: [5], 4: [], 5: [6, 7], 6: [], 7: [3]}
def iterative_dfs(start_v):
discovered = []
print(f"스택에 {start_v}를 넣습니다.")
stack = [start_v] # 스택에 인접 간선(다음 탐색 순서)를 집어넣음.
print(f"현재 스택 상태: {stack}")
while stack:
v = stack.pop()
print(f"스택에서 {v}를 꺼냅니다.")
print(f"현재 스택 상태: {stack}")
if v not in discovered:
print(f"{v}는 미방문 노드입니다. 방문 처리 후 방문 리스트에 추가합니다.")
discovered.append(v)
for w in graph[v]:
print(f"{v}의 다음 노드 {w}를 스택에 추가합니다.")
stack.append(w)
return discovered
print(iterative_dfs(1))
스택에 1를 넣습니다.
현재 스택 상태: [1]
스택에서 1를 꺼냅니다.
현재 스택 상태: []
1는 미방문 노드입니다. 방문 처리 후 방문 리스트에 추가합니다.
1의 다음 노드 2를 스택에 추가합니다.
1의 다음 노드 3를 스택에 추가합니다.
1의 다음 노드 4를 스택에 추가합니다.
스택에서 4를 꺼냅니다.
현재 스택 상태: [2, 3]
4는 미방문 노드입니다. 방문 처리 후 방문 리스트에 추가합니다.
스택에서 3를 꺼냅니다.
현재 스택 상태: [2]
3는 미방문 노드입니다. 방문 처리 후 방문 리스트에 추가합니다.
3의 다음 노드 5를 스택에 추가합니다.
스택에서 5를 꺼냅니다.
현재 스택 상태: [2]
5는 미방문 노드입니다. 방문 처리 후 방문 리스트에 추가합니다.
5의 다음 노드 6를 스택에 추가합니다.
5의 다음 노드 7를 스택에 추가합니다.
스택에서 7를 꺼냅니다.
현재 스택 상태: [2, 6]
7는 미방문 노드입니다. 방문 처리 후 방문 리스트에 추가합니다.
7의 다음 노드 3를 스택에 추가합니다.
스택에서 3를 꺼냅니다.
현재 스택 상태: [2, 6]
스택에서 6를 꺼냅니다.
현재 스택 상태: [2]
6는 미방문 노드입니다. 방문 처리 후 방문 리스트에 추가합니다.
스택에서 2를 꺼냅니다.
현재 스택 상태: []
2는 미방문 노드입니다. 방문 처리 후 방문 리스트에 추가합니다.
2의 다음 노드 5를 스택에 추가합니다.
스택에서 5를 꺼냅니다.
현재 스택 상태: []
[1, 4, 3, 5, 7, 6, 2]위상 정렬(topology sort)
순서가 있는 작업을 차례대로 수행해야 할 때 그 순서를 결정하기 위한 알고리즘
DAG에서 위상 정렬을 수행할 수 있다.
여러 개의 답이 존재할 수 있다.
위상 정렬로 알 수 있는 사실(해결책)
1. 위상 정렬이 가능한지(사이클이 없는지)
2. ('1'이 충족한다면) 위상 정렬의 결과가 무엇인지
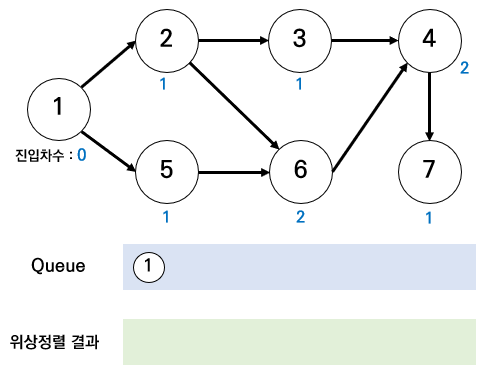
위상 정렬 순서
(0. 배열에 노드와 진입 차수 명시)
1. 진입차수가 0인 정점(시작점)을 큐에 삽입
2. 큐에서 원소를 꺼내 연결된 모든 간선을 제거
2-1. 진입 차수 갱신
3. 간선 제거 이후 진입차수가 0이 된 정점을 큐에 삽입
4. 2~3반복
4-1. 원소 방문 전에 큐가 비면 사이클 존재(위상 정렬 불가)
4-2. 큐가 비었을 때 모든 원소를 방문했다면 큐에서 꺼낸 순서가 위상 정렬
DAG(Direct Acyclic Graph)
유향 비순환 그래프: 순환하는 싸이클이 존재하지 않고 일방향성인 그래프
acyclic(비순환)
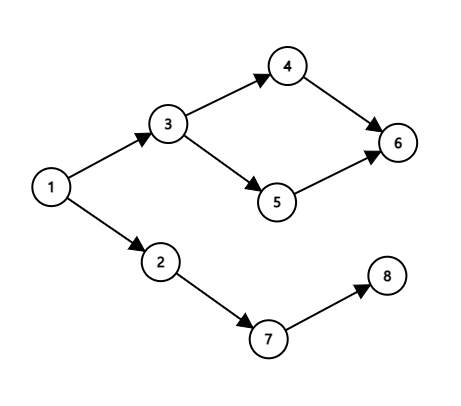
진입 차수: 해당 노드로 들어오는 차수
파이썬 문법
int()는 정수 형태의 문자만 정수로 변환할 수 있다.(소수 형태의 문자는 못 바꿈)
소수 형태의 문자를 형변환 하려면 float() 사용
