자료구조
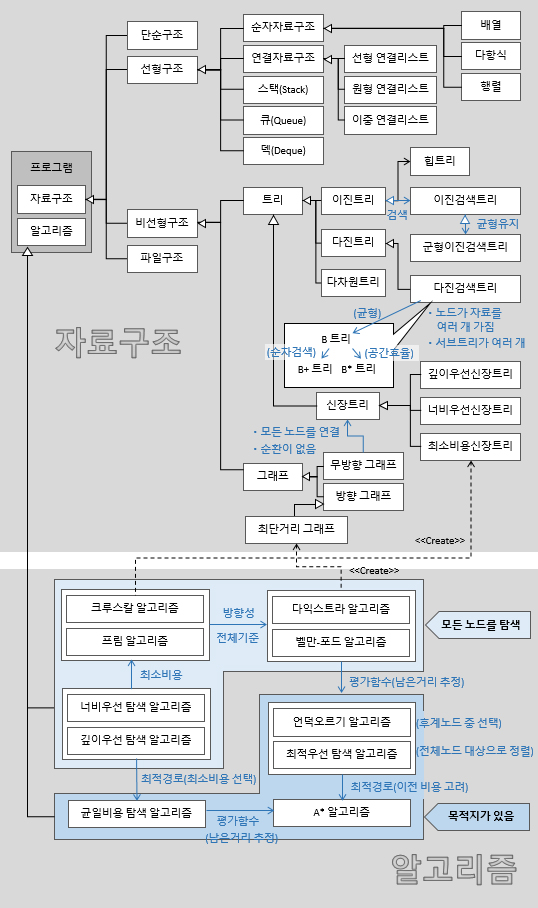
이 그림을 보니까 무엇을 공부해야 할지 전체적인 계획이 확실히 잡힘!
트리 학습 키워드
트리 종류가 너무 많아서 어떤 걸 공부해야 할지 정리해봄.
1. 트리 ✅
2. 이진 트리 ✅
3. 이진 탐색 트리 ✅
4. 균형 이진 탐색 트리 ⬇️
4.1 RB 트리 ❌
5. 최소 신장 트리(Minimun Spanning Test, MST) 🔥
6. 탐색 ⬇️
7.1 깊이 우선 탐색(DFS) ✅
8.2 너비 우선 탐색(BFS) ✅
자료구조
백준 1991 트리 순회
노드와 트리 자체를 클래스로 구현
N = int(input())
datas = [input().strip() for _ in range(N)]
class Node:
def __init__(self, data):
self.data = data
self.left = None
self.right = None
def set_children(self, left_node=None, right_node=None):
self.left = left_node
self.right = right_node
class Tree:
def __init__(self):
self.root = None
def set_root(self, root_node):
self.root = root_node
def get_root(self):
return self.root
def make_node(self, data, left, right):
node = Node(data)
node.set_children(left, right)
return node
def preorder_traversal(self, node):
result = []
if node:
result.append(node.data)
result.extend(self.preorder_traversal(node.left))
result.extend(self.preorder_traversal(node.right))
return result
def inorder_traversal(self, node):
result = []
if node:
result.extend(self.inorder_traversal(node.left))
result.append(node.data)
result.extend(self.inorder_traversal(node.right))
return result
def postorder_traversal(self, node):
result = []
if node:
result.extend(self.postorder_traversal(node.left))
result.extend(self.postorder_traversal(node.right))
result.append(node.data)
return result
tree_map = {}
for data in datas:
root, left, right = data.split()
if left == ".":
left = None
if right == ".":
right = None
tree_map[root] = (left, right)
tree = Tree()
def build_tree(root_key):
left_key, right_key = tree_map[root_key]
if left_key is not None:
left_node = build_tree(left_key)
else:
left_node = None
if right_key is not None:
right_node = build_tree(right_key)
else:
right_node = None
return tree.make_node(root_key, left_node, right_node)
root_key = "A"
tree.set_root(build_tree(root_key))
preorder = tree.preorder_traversal(tree.get_root())
inorder = tree.inorder_traversal(tree.get_root())
postorder = tree.postorder_traversal(tree.get_root())
print("".join(preorder))
print("".join(inorder))
print("".join(postorder))문제 풀이에는 적절하지 않는 형태지만 트리를 직접 구현해 볼 목적으로 작성해 봄. 클래스 활용법을 확실히 알게 되었음.
간단한 풀이
N = int(input())
tree = dict()
for i in range(N):
root, left, right = input().strip().split()
tree[root] = (left, right)
def preorder(v):
result = []
if v != '.':
result.append(v)
result.extend(preorder(tree[v][0]))
result.extend(preorder(tree[v][1]))
return result
def inorder(v):
result = []
if v != '.':
result.extend(inorder(tree[v][0]))
result.append(v)
result.extend(inorder(tree[v][1]))
return result
def postorder(v):
result = []
if v != '.':
result.extend(postorder(tree[v][0]))
result.extend(postorder(tree[v][1]))
result.append(v)
return result
print("".join(preorder('A')))
print("".join(inorder('A')))
print("".join(postorder('A')))트리 순회 코딩하면서 재귀가 조금 더 이해됨
UnboundLocalError
변수가 로컬 스코프에서 정의되지 않았을 때 발생하는 예외
UnboundLocalError 발생 코드
def build_tree(root_key):
left_key, right_key = tree_map[root_key]
if left_key is not None:
left_node = build_tree(left_key)
if right_key is not None:
right_node = build_tree(right_key)
return tree.make_node(root_key, left_node, right_node)left_key 또는 right_key가 None이면 함수 내에서 left_node 또는 right_node에 값이 할당되지 않아 return문에서 재귀 호출을 할때 인자가 넘어가지 않아서 UnboundLocalError가 발생하였음. 다음과 같이 처리 가능
해결 방법
함수 내에서 변수를 초기화(None값을 할당)해주면 됨
...
# 방법1. 상단에 변수 초기화
left_node = None
right_nonde = None
(이하 if문..)
# in문 내에서 변수 초기화
if ...
...
else:
left_node = None로컬 스코프에서 로컬 변수에 어떤 값도 할당되지 않으면 사용할 수 없음!
(None이라도 할당해서 초기화해줘야 함)
프리 오더 순서만 가지고는 트리를 재현해 낼 수 없다!
자가 균형 이진 탐색 트리
삽입, 삭제 시 자동으로 높이를 작게 유지하는 노드 기반 이진 탐색 트리
(높이를 가능한 낮게 유지한다!)
자가 균형 이진 탐색 트리의 종류
1. AVL트리
2. 레드-블랙 트리(효율성이 좋아 실무에서도 빈번하게 쓰임!)
이진 탐색 트리 정렬 hands on
(높이 균형 BST: 서브 트리 간 깊이 차이가 1 이하)
# 오름차순으로 정렬된 배열을 이진 탐색 트리로 정렬하는 방법
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right
def sortedArrayToBST(nums):
if not nums:
return None
mid = len(nums) // 2
root = TreeNode(nums[mid])
root.left = sortedArrayToBST(nums[:mid])
root.right = sortedArrayToBST(nums[mid + 1 :])
return root
def dfs(root):
result = []
if root:
result.append(root.val)
result.extend(dfs(root.left))
result.extend(dfs(root.right))
return result
arr = [-10, -7, -3, 0, 5, 7, 9]
root = sortedArrayToBST(arr)
print(dfs(root))파이썬에서 슬라이싱은 범위를 넘어가도 오류가 발생하지 않고 빈 배열을 반환한다.
a = ["a"] print(a[2:5]) # []
백준 5639 이진 검색 트리
복습
이진 검색 트리: 이진 트리 중 왼쪽 자식은 노드보다 작고, 오른쪽 자식은 노드보다 큼
탐색 시간 복잡도 O(log n)
클래스 활용하며 코딩했으나 재귀 호출 제한 넘고, 시간 초과 뜸
preorder = [50, 30, 24, 5, 28, 45, 98, 52, 60]
while True:
try:
input.append(int(input().strip()))
except:
break
class Node:
def __init__(self, val, left=None, right=None):
self.val = val
self.left = left
self.right = right
class Tree:
def __init__(self):
self.root = None
def build_tree_by_preorder(self, preorder):
if not preorder:
return None
root = Node(preorder[0])
i = 1
while i < len(preorder) and preorder[i] < root.val:
i += 1
root.left = self.build_tree_by_preorder(preorder[1:i])
root.right = self.build_tree_by_preorder(preorder[i:])
return root
def postorder_traversal(self, node):
result = []
if node:
result.extend(self.postorder_traversal(node.left))
result.extend(self.postorder_traversal(node.right))
result.append(node.val)
return result
tree = Tree()
root = tree.build_tree_by_preorder(preorder)
tree.root = root
result = tree.postorder_traversal(tree.root)
for val in result:
print(val)
이진 검색 트리는 최악의 경우(균등하게 배치되지 않는 경우) O(n)의 시간 복잡도가 생길 수 있어서 나온 게 자가 균형 이진 탐색 트리
코드 단순화
import sys
sys.setrecursionlimit(10 ** 9)
preorder = []
while True:
try:
preorder.append(int(input().strip()))
except:
break
def preorder_to_postorder(preorder):
if not preorder:
return []
root = preorder[0]
postorder = []
left_preorder = []
right_preorder = []
for i in range(1, len(preorder)):
if preorder[i] < root:
left_preorder.append(preorder[i])
else:
right_preorder.append(preorder[i])
left_postorder = preorder_to_postorder(left_preorder)
right_postorder = preorder_to_postorder(right_preorder)
postorder.extend(left_postorder)
postorder.extend(right_postorder)
postorder.append(root)
return postorder
postorder = preorder_to_postorder(preorder)
for val in postorder:
print(val)재귀 오류 뜨는 경우 재귀 깊이 강제로 늘려주기
sys.setrecursionlimit(10 ** 9)
이진 탐색 트리 배열 구조
1. 전위 탐색
[루트, 루트의 왼쪽 트리, 루트의 오른쪽 트리]
2. 중위 탐색
[루트의 왼쪽 트리, 루트, 루트의 오른쪽 트리]
3. 후위 탐색
[루트의 왼쪽 트리, 루트의 오른쪽 트리, 루트]
탐색은 항상 루트부터 시작하기!
그래프가 도대체 뭐야?
그래프는 용어 자체가 회로다!!! 이걸 알아야 다양한 그래프가 이해된다!!
간선과 노드로 구성된 자료 구조
특징
1. 방향성 vs 무방향성
2. 가중치 vs no가중치
3. 순환 vs 비순환
4. 연결 vs 비연결
그래프는 모든 노드가 다 연결되어야 하는 건 아니다.
중간이 끊어진 그래프를 비연결 그래프라고 한다.
완전 그래프(Complete Graph)
각 정점이 다른 모든 정점들과 연결되어 있는 그래프를 Kn이라고 함.
완전 그래프 간선의 개수: nC2 = n(n-1)/2
트리가 도대체 뭐야?
순환하지 않는 단방향 그래프!
조건
1. 트리는 1개의 루트를 갖는다.
2. 모든 노드는 1개의 부모를 갖는다.
그래프 > 트리 > 이진 트리
이진 트리 > (이진 탐색 트리, 정 이진 트리, 완전 이진 트리, 포화 이진 트리)
완전 이진 트리 중 힙 속성(최소힙, 최대힙)을 만족하는 자료구조를 힙이라고 한다.
(힙은 완전 이진 트리 기반의 자료 구조)
트리 자료 구조 안에 힙이 있다.
힙은 특정 조건을 만족하는 이진 트리이다.
최소 힙: 부모 노드 <= 자식 노드
최대 힙: 부모 노드 >= 자식 노드
그래프는 사이클이 있는 그래프와 사이클이 없는 그래프로 나뉜다.
이 중에서 사이클이 없는 그래프를 특별히 트리라고 한다.
트리는 재귀 순회가 자연스럽다. 이유는 트리는 자기 참조 자료구조이기 때문
트리를 어떻게 표현해야 할까?
- 인접 행렬
- 인접 리스트
인접 행렬(Adjacency Matrix)
행과 열이 노드를 나타내는 2차원 배열
노드 A와 노드 B가 인접하면 해당 행과 열의 원소에 연결 여부를 나타내는 값을 넣는다.
인접한 노드는 배열 내에서 직접적으로 연결된 노드
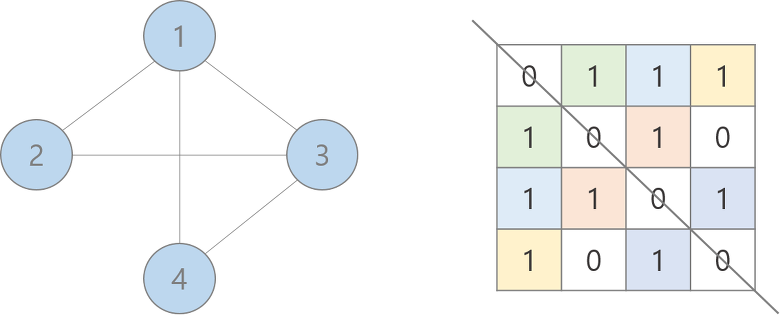
인접 행렬은 그래프를 2차원 행렬로 바꾼 것!
행렬의 (1의 합) = 변의 수 * 2
'인접(adjacency)'의 뜻은 해당 노드에 직접 연결되어 있는 노드들을 의미함!
# 그래프의 노드 개수
num_nodes = 4
# 초기화된 인접 행렬 생성 (4 x 4)
adjacency_matrix = [[0] * num_nodes for _ in range(num_nodes)]
# 간선 추가 함수
def add_edge(matrix, start, end):
# 노드 사이의 연결을 나타내기 위해 해당 셀을 1로 설정
matrix[start][end] = 1
matrix[end][start] = 1 # 무방향 그래프인 경우 양쪽으로 설정
# 간선 추가 예시
add_edge(adjacency_matrix, 0, 1) # 인덱스 0과 인덱스 1해 해당하는 두 노드를 간선에 추가
add_edge(adjacency_matrix, 0, 2)
add_edge(adjacency_matrix, 1, 2)
add_edge(adjacency_matrix, 2, 3)
# 인접 행렬 출력
print(adjacency_matrix)
# 출력 결과
# [
# [0, 1, 1, 0],
# [1, 0, 1, 0],
# [1, 1, 0, 1],
# [0, 0, 1, 0]
# ]
# 0---1
# | /
# 2---3인접 행렬은 어디에 활용할 수 있을까?
1. 경로의 수
(길이가 2인 경우)인접 행렬을 2번 곱하면 나오는 수가 경로의 수가 된다!
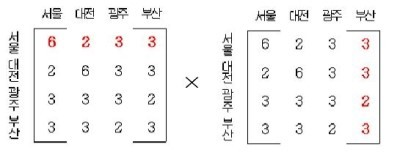
2. 도형의 수
그래프에서 삼각형, 사각형 등의 도형을 찾을 수 있음.
단, 삼각형의 예를 들면 하나의 삼각형에서 6가지의 방향성이 있으니 최종적으로는 전체 경로에서 6을 나눠줘야 함.
즉, 인접 행렬로 경로를 구한 경우 중복된 경우를 계산해서 빼야 함.
인접 리스트(adjacency List)
각 노드의 인접한 노드들을 연결 리스트나 배열 등의 자료구조로 나타냄
해당 노드 인접 리스트에 직접적으로 연결된 노드
# 그래프의 노드 개수
num_nodes = 4
# 초기화된 인접 리스트 생성
adjacency_list = {}
# 간선 추가 함수
def add_edge(graph, start, end):
if start not in graph:
graph[start] = [] # 시작 노드가 없는 경우 초기화
if end not in graph:
graph[end] = [] # 끝 노드가 없는 경우 초기화
# 양쪽 노드에 연결 추가 (무방향 그래프)
graph[start].append(end)
graph[end].append(start)
# 간선 추가 예시
add_edge(adjacency_list, 0, 1)
add_edge(adjacency_list, 0, 2)
add_edge(adjacency_list, 1, 2)
add_edge(adjacency_list, 2, 3)
print(adjacency_list)
# 출력 결과
# {
# 0: [1, 2],
# 1: [0, 2],
# 2: [0, 1, 3],
# 3: [2]
# }
# 0---1
# | /
# 2---3평면 그래프
엣지가 겹치지 않는 그래프
(2차원 평면상에서 겹치지 않아야 한다.)
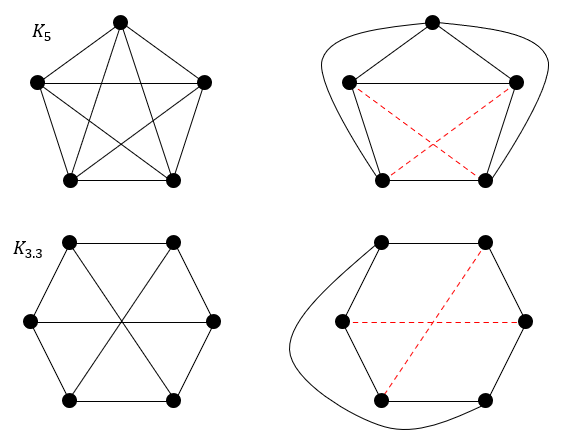
평면 그래프는 단순히 모양만 보고 판단하면 안 된다. 노드 사이의 간선 길이는 자유롭게 조절할 수 있다. 간선의 길이를 조정해도 간선이 겹칠 때만 평면 그래프로 판단할 수 있다.
(이것도 평면 그래프)
평면 그래프 공식
v - e + f = 2
(꼭짓점) - (변) + (면) = 2
면은 외부 영역도 포함 해야 함!
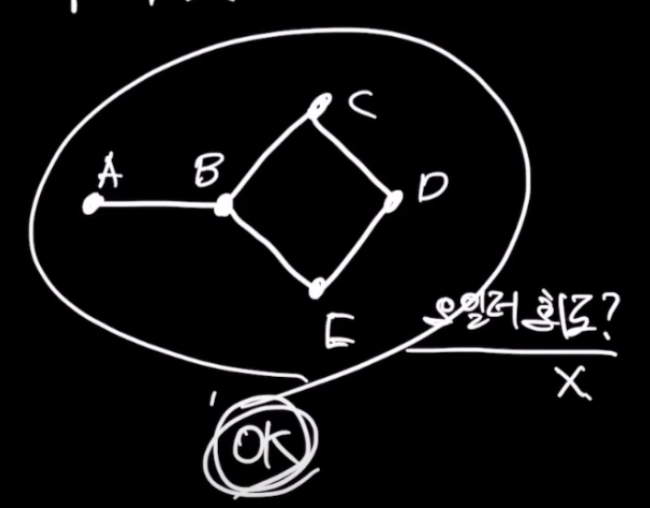
오일러 그래프(간선을 기준으로)
오일러 경로: 그래프에 존재하는 모든 간선을 한 번씩 방문하는 연속된 경로
오일러 그래프(회로): 오일러 경로에서 시작점과 도착점이 같은 경우
오일러 그래프는 모든 '변'을 지나야 한다.
오일러 그래프는 한 붓 그리기가 가능한 그래프이디만, 한 붓 그리기가 가능하다고 해서 모두 오일러 그래프는 아니다.
오일러 그래프가 성립하는 조건
모든 꼭지점 차수가 짝수 -> 오일러 회로를 같는다.
오일러 경로가 성립하는 조건
모든 꼭지점 차수가 짝수 or 단 2개의 정점만 차수가 홀수
해밀턴 그래프(노드를 기준으로)
해밀턴 경로: 모든 정점을 한 번씩 방문하는 경로
해밀턴 그래프(회로): 해밀턴 경로에서 시작점과 도착점이 같은 경우
해밀턴 그래프는 모든 변을 지날 필요는 없다.
수형도(트리)
모두가 연결되어 있지만 회로가 아니다.
v - e = 1 이면 수형도다.
(노드 - 간선 = 1)
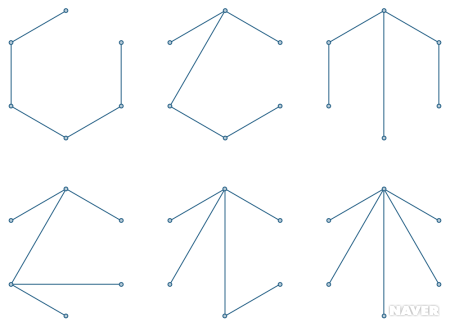
(참고) 수형도가 아닌 걸(그래프)를 수형도로 만든 걸 생성 수형도라고 한다.
주요 그래프
백준 11724 연결 요소의 개수
연결 요소(Connected Component): 그래프 내에서 서로 연결된 노드들의 그룹
그래프 자료구조 구현해 봄
import sys
from collections import defaultdict
sys.setrecursionlimit(10**9)
class Graph:
def __init__(self) -> None:
self.graph = defaultdict(list)
def add_edge(self, v: int, u: int) -> None:
self.graph[u].append(v)
self.graph[v].append(u)
def dfs(self, v: int, visited: list) -> None:
visited[v] = True
for neighbor in self.graph[v]:
if not visited[neighbor]:
self.dfs(neighbor, visited)
def conneted_components(self) -> int:
visited = [False] * (N + 1)
count = 0
for v in range(1, N + 1):
if not visited[v]:
self.dfs(v, visited)
count += 1
return count
N, M = map(int, sys.stdin.readline().strip().split())
g = Graph()
for _ in range(M):
v, u = map(int, sys.stdin.readline().strip().split())
g.add_edge(v, u)
count = g.conneted_components()
print(count)처음에 계속 재귀 에러, 시간 초과 발생함.
input()을 readline()으로 변경하자 채점 시작함.
앞으로 input()말고 무조건 readline() 쓰자!
이거 5시간 걸림. 하지만 시간을 들인 가치가 있었음.
초기에 그래프를 구성할 때, 간선이 없으면 그래프가 구성되지 않아서
간선이 없는 단일 정점은 탐색하지 않아서 카운트가 올라가지 않았음.
탐색을 해야 하는 횟수를 len(graph)로 하지 않고, 입력 값의 N을 기준으로 했더니 문제가 해결됨.
최소 신장 트리(Minimum Spanning Tree)
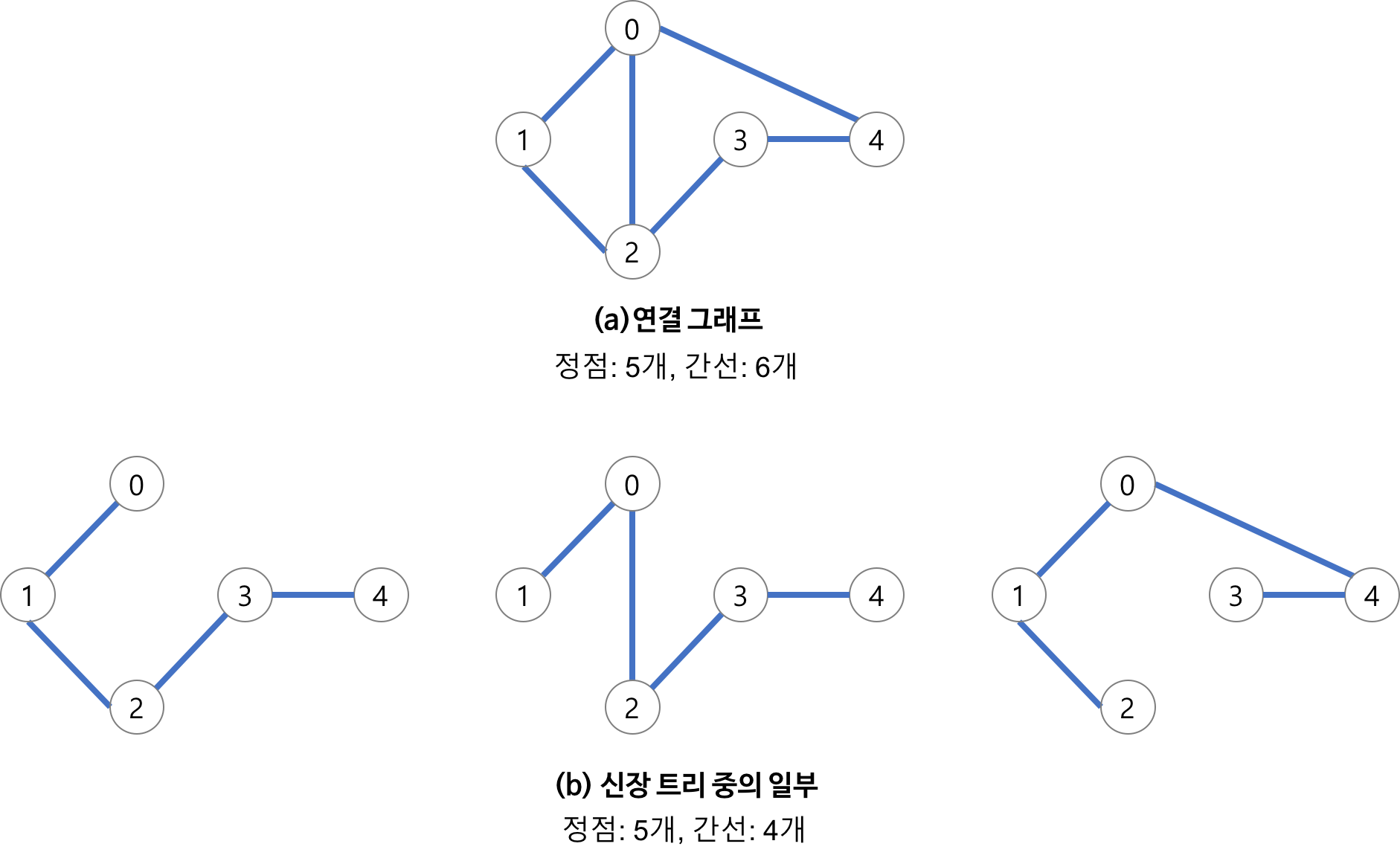
왜 '신장'인가?
신장은 영어의 spanning(포괄적인, 모든 것을 포함하는)을 번역한 것.
신장 트리는 모든 노드를 연결하는 트리라고 볼 수 있다!(단, 순환 구조가 없어야 함)
신장 트리: n개의 정점을 포함하는 무향 그래프에서 n개의 정점과 n-1개의 간선으로 구성된 트리
(모든 노드를 연결하면서 순환하지 않아야 함)
최소 신장 트리: 신장 트리 중 가중치의 합이 최소인 신장 트리
신장 트리는 그래프에 속하는건데 왜 '그래프'라고 하지 않고 '트리'라고 하지?
'트리'라는 용어 자체가 모든 노드를 연결하면서 순환하지 않는 구조를 말한다.
즉, 신장 트리는 그래프에서 순환하지 않는 부분이기 때문에 신장 트리 자체는 그래프가 아닌 트리이다.
즉, 신장 트리는 원래 그래프에서 파생된 트리이다.
최소 신장 트리를 구할 수 있는 알고리즘
- 크루스칼 알고리즘(Kruskal's Algorithm)
- 프림 알고리즘(Prim's Algorithm)
(MST) 1. 크루스칼 알고리즘(Kruskal's Algorithm)
특징
1. 간선의 가중치를 기준으로 MST를 구축하는 알고리즘
2. 초기에는 그래프의 모든 노드를 개별 트리로 간주
3. 간선들을 가중치 순으로 정렬, 가장 작은 가중치부터 간선부터 MST에 추가
(단, 사이클을 형성하는 간선은 무시)
4. 모든 노드가 MST에 포함될 때까지 '3'을 반복
(MST) 2. 프림 알고리즘(Prim's Algorithm)
특징
1. 시작 노드에서 출발해서 MST를 구축하는 알고리즘
2. 초기에는 시작 노드만 MST에 있음, 그래프의 모든 간선은 고려되지 않음
3. 각 단계에서 MST에 연결되지 않은 노드 중 최소 가중치 간선을 선택하여 MST에 추가
4. 모든 노드가 MST에 포함 될때까지 '3'을 반복
최소 신장 트리 알고리즘은 내일 한다.