일찍 일어나서 평소보다 30분 일찍 강의실 옴(07:30)
눈 떠서 안 졸리면 그냥 일찍 나오기
아스키 코드, 유니코드, UTF-8 이해함!
어제 밤에 한권으로 읽는 컴퓨터 구조와 프로그래밍 책 보고 아스키 코드, 유니코드, UTF-8 이해함! 인코딩 후에 디코딩 한다는 사실을 몰라서 이해에 어려웠음.
핵심은 코드 포인터 != (전송)비트라는 것! 코드 포인터를 어떻게 비트로 변환할지는 인코딩 방식에 따라 다름!
간단히 머리 속에 있는 거 적어봄(복기용)
1. 아스키코드(미국정보교환표준부호)
컴퓨터는 미국이 만들어서 처음에는 알파벳, 숫자, 특수 문자 등 7비트를 가지고 만든 문자셋. 여기서 문자셋이란 문자와 숫자를 매칭시킨 거임.(왜냐면 컴퓨터는 모든 걸 수로 표현하니까)
근데 이제 컴퓨터를 여러 나라에서 쓰기 시작하면서 각 나라들이 독자적인 문자셋을 쓰면서 문제가 생김. 그래서 유니코드가 나옴.
아스키코드는 7비트이지만 현대 컴퓨터는 주로 8비트 단위를 사용함. 통신을 할 때도 마찬가지. 그래서 나머지 1비트를 패리티 비트(오류 검출용)이나 확장 아스키 코드에 씀.
2. 유니코드
각 나라들이 지들 맘대로 문자셋 쓰는 걸 천하통일한 문자셋. 2바이트로(16비트) 표현할 수 있는 코드 포인트 범위에서 전세계 모든 문자를 매핑하는 걸로 시작했는데 지금은 문자가 너무 많아져서 2바이트로 부족함.(그래서 더 늘었음)
애당초 유니코드는 '전송'이 핵심이 아니라 '맵핑'이 핵심이기 때문에 코드 포인트가 부족하면 그냥 코드 포인트를 늘리면 됨. 정확히 2바이트에 매핑하는 게 아니라 각 문자마다 코드 포인트를 할당했다고 보는 게 맞음.(2바이트가 핵심이 아님) 한글은 유니코드에서 2바이트로 표현할 수 있는 코드 포인트에 할당되어 있음.(UTF-8로 인코딩 하면 3바이트로 늘어남)
아스키코드와 유니코드는 코드 포인트가 동일함. 그래서 유니코드를 적용한 곳에서 아스키코드를 받아도 잘 돌아감. 즉 유니코드는 아스키 코드와 호환성이 100%라는 말. 유니코드를 만들 때 아스키코드와 호환성을 중요하게 생각했다고 함.(근데 그럴 수밖에 없는데 컴퓨터는 그냥 다 영어임..)
근데 여기서 문제가 생김. 유니코드는 단순히 문자와 숫자를 맵핑시켜 놓은 코드표임.(정확히는 문자셋이 유니코드의 전부는 아니지만 그냥 우선 문자셋만 보고 생각함. 일련의 표준이 유니코드임.) 그래서 이 코드를 전송할 때 어떻게 전송해야 하는지는 정해지지 않았음.
그럼 그냥 유니코드를 바로 비트로 변환해서 보내면 되지 않냐? 근데 여기서 문제가 있음. 먼저 가장 많이 쓰이는 영어, 숫자는 8비트면 충분함.(7비트만 현대 컴퓨터는 8바이트 단위이므로 그냥 8비트라고 함.)
근데 유니코드 코드를 그대로 전송하면 1바이트면 충분한 아스키코드가 2바이트로 용량이 100% 커져버림. 영어와 숫자가 많은 부분을 차지하는 현대 컴퓨터에서 이건 너무 낭비임. 그래서 유니코드 코드표를 효율적으로 전송할 수 있는 방식이 등장하는데 그 중에서 가장 많이 쓰이는 게 인터넷에서 자주볼 수 있는 UTF-8임.
유니코드만 따로 더 공부해야 할 것 같음. 유니코드 코드포인터가 어떤 식으로 할당되어 있는지 찾아보자.
3. UTF-8
이름부터가 유니코드 트랜스포매이션 포맷임. 즉, 유니코드를 잘 포맷팅해서 전송하는 게 목적임.
UTF-8은 2바이트의 유니코드는 1~4바이트로 변환해서 전송함. 아스키 코드는 7비트면 충분하니까 유니코드에서 앞쪽 8개 비트는 버리고 뒤쪽 8개 비트만 전송해도 됨. 유니코드 대비 전송 비용이 절반으로 줄어드는 거임! 그리고 나머지는 적절하게 2~4바이트로 변환해서 전송함.
근데 컴퓨터는 연속된 시퀀스로 비트를 받을 거 아녀? 그럼 이걸 어떻게 구분하느냐? 인코딩할 때 이렇게 함.
1바이트: 가장 왼쪽 비트에 0을 붙임(아스키 코드는 유니코드랑 인코딩된 UTF-8이랑 코드 포인트가 모두 같음)
2바이트: 첫 번째 바이트의 MSB(가장 큰 비트) 3비트를 110, 두 번째 바이트를 10으로 함.
3바이트: 첫 번째 바이트 1110, 두 번째 바이트 10, 세 번째 바이트 10
4바이트: 첫 번째 바이트 11110, 두 번째 바이트 10, 세번째 바이트 10, 네 번째 바이트 10
규칙이 있음. 1바이트는 그냥 0이고, 나머지는 첫 번째 바이트의 1의 개수가 전체 바이트를 나타내고 0을 붙임. 나머지는 10으로 세팅.
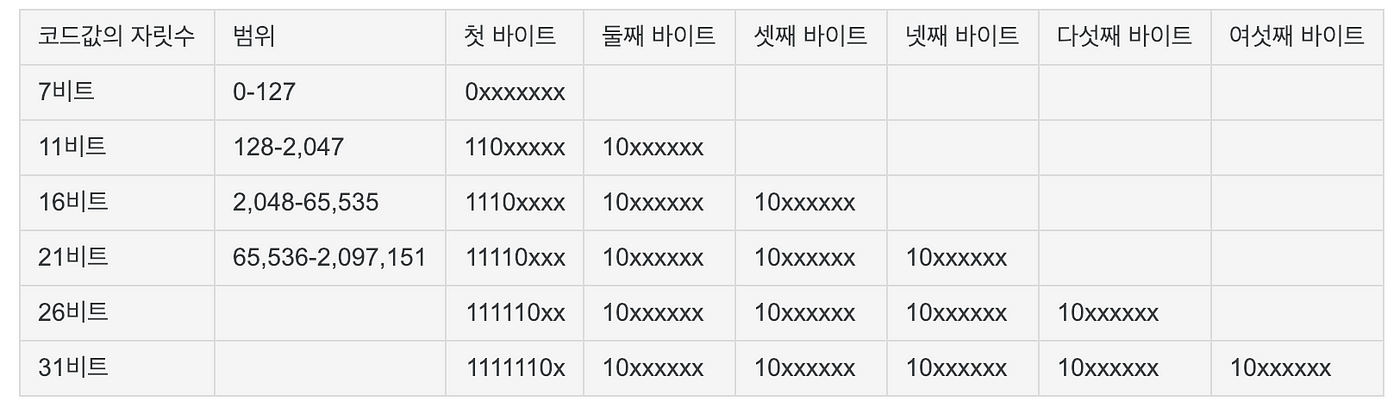
그림에는 왜 6바이트냐? 원래 유니코드는 만들어질 떄 최대 6바이트까지 할당하는 거로 만들었는데 2003년 11월에 4바이트로 제한하는 걸로 수정됨.
이렇게 UTF-8로 인코딩 한 후에 통신해서 네트워크로 쭉 보내면 로컬에서는 이걸 받아서 디코딩을 해서 다시 유니코드로 변환한다. 이걸 몰라서 몇 달이나 이해 못했음!!!!
자, 근데 여기서 의문이 든다. 아니 그냥 평균적으로 유니코드 그대로 2바이트로 보내면 되지 UTF-8로 바꾸면 1~4바이트니까 손해 아녀?
아니다. 왜냐면 많은 케이스가 영어, 숫자인 1바이트에 포함되고 나머지 많은 경우도 2바이트 선에서 정리됨.(근데 한글은 3바이트)
3~4바이트는로 갈수록 사용 빈도가 떨어지니까 이렇게 가변 길이로 하는 게 전체적으로 이득임.
그리고 여기서 또 의문이 든다. 아니, 각 바이트 앞자리에 전송되는 바이트 수를 구분하려고 붙이는 수가 너무 많아서 비트가 너무 낭비되는 거 아녀?
이것도 아니다. 왜냐면 이렇게 비트를 낭비해도 이 세상에 존재하는 문자를 4바이트에 매핑하는 건 충분히 남아 돈다. 그리고 어차피 전송할 때는 8비트 단위로 나가야 되니까 앞에 비트를 그냥 낭비하느니 차라리 특별한 정보를 넣어 오히려 전송 오류 같은 걸 방지하는데 쓰는 게 낫다.
참고로 유니코드는 계속 추가되고 있다고 한다.(이모지 같은 거) 그렇다고 UTF-8에 뭔가 변화가 있는 건 아니다. UTF-8은 어떻게 잘 전송할지를 정하는 규약이다. 그니까 유니코드가 추가되어도 그냥 자기가 가지고 있는 규칙에 따라 비트를 잘 바꿔서 보내면 되는 거다.
근데 1~4바이트까지 매핑하면서 왜 이름에 8이 들어가냐?
기본 단위가 8비트라는 말
UTF-16, UTF-32는 뭐냐?
기본 단위가 각각 16비트, 32비트라는 말. 그니까 UTF-16은 8비트나 24비트에 매핑 안한다. 16아니면 32비트임.
UTF-32는 기본적으로 32비트에 유니코드를 할당한다.
딱 봐도 뭔가 낭비다.(장점이 없다는 건 아님, 고정 길이가 주는 장점이 있음.) 그래서 지금은 다 UTF-8을 쓴다.
코테를 객체지향 + 의존성 주입으로 풀어보기
알고리즘 정답만 맞추는 게 아니라 트리 자료 구조를 객체 지향으로 구현해 보고 의존성 주입으로 알고리즘 풀어 보았음! (7시 30분부터 15시까지 이것만 함)
- 노드 클래스와 트리 클래스로 나누어서 단일 책임 원칙 구현해 봄.
- 변수에
_붙이고 변수명으로 직접 접근이 아니라 게터와 세터로만 데이터에 접근, 조작할 수 있도록 은닉화 함.- 트리 클래스 안에서 Node를 직접 생성하지 않고, 매개변수로 클래스 자체를 전달해서 의존성 주입(DI) 구현해 봄.
(이렇게 생성자에 주입하는 걸 의존성 주입 중 생성자 방식이라고 하는데.. GPT는 뻘소리 많이 해서 맞는지는 모름)
백준 1991 트리 순회
import sys
sys.setrecursionlimit(10**6)
class Node:
def __init__(self, val):
self._val = val
self._left = None
self._right = None
def get_val(self):
return self._val
def set_val(self, val):
self._val = val
def get_left_child(self):
return self._left
def set_left_child(self, left):
self._left = left
def get_right_child(self):
return self._right
def set_right_child(self, right):
self._right = right
class Tree:
def __init__(self, NodeClass, root_node=None):
self._root = root_node
self._tree_map = {}
self.NodeClass = NodeClass
def set_tree_root(self, root):
self._root = root
def get_tree_root(self):
return self._root
def set_tree_map(self, key, left, right):
if left == ".":
left = None
if right == ".":
right = None
self._tree_map[key] = [left, right]
def get_tree_map(self):
return self._tree_map
def build_tree(self, root_key):
left_key, right_key = self.get_tree_map()[root_key]
if left_key is not None:
left_node = self.build_tree(left_key)
else:
left_node = None
if right_key is not None:
right_node = self.build_tree(right_key)
else:
right_node = None
return self.make_node(root_key, left_node, right_node)
def make_node(self, root_key, left_node=None, right_node=None):
root_node = self.NodeClass(root_key)
root_node.set_left_child(left_node)
root_node.set_right_child(right_node)
return root_node
def preorder_traversal(self, node):
result = []
if node:
result.append(node.get_val())
result.extend(self.preorder_traversal(node.get_left_child()))
result.extend(self.preorder_traversal(node.get_right_child()))
return result
def inorder_traversal(self, node):
result = []
if node:
result.extend(self.inorder_traversal(node.get_left_child()))
result.append(node.get_val())
result.extend(self.inorder_traversal(node.get_right_child()))
return result
def postorder_traversal(self, node):
result = []
if node:
result.extend(self.postorder_traversal(node.get_left_child()))
result.extend(self.postorder_traversal(node.get_right_child()))
result.append(node.get_val())
return result
# 입력값 받기
N = int(sys.stdin.readline().strip())
datas = []
for data in range(N):
root, left, right = sys.stdin.readline().strip().split()
datas.append((root, left, right))
# 트리 객체 생성
tree = Tree(Node)
for data in datas:
root, left, right = data
tree.set_tree_map(root, left, right)
root_key = "A"
root_node = tree.build_tree(root_key)
tree.set_tree_root(root_node)
root = tree.get_tree_root()
print("".join(tree.preorder_traversal(root)))
print("".join(tree.inorder_traversal(root)))
print("".join(tree.postorder_traversal(root)))그래프 복습
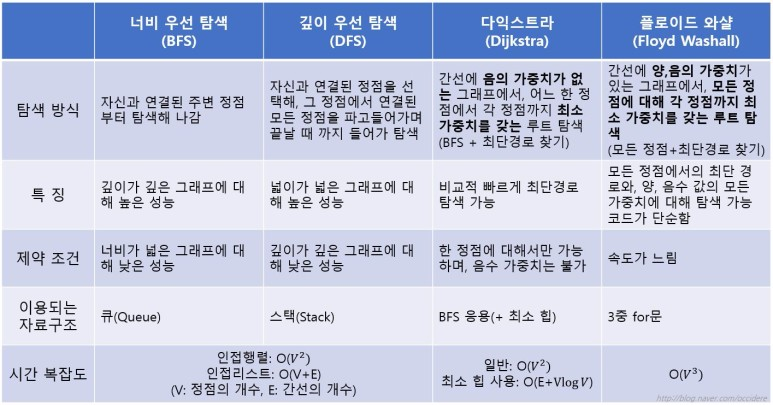
그래프를 탐색하는 방법
위상 정렬을 이해하기 위해서
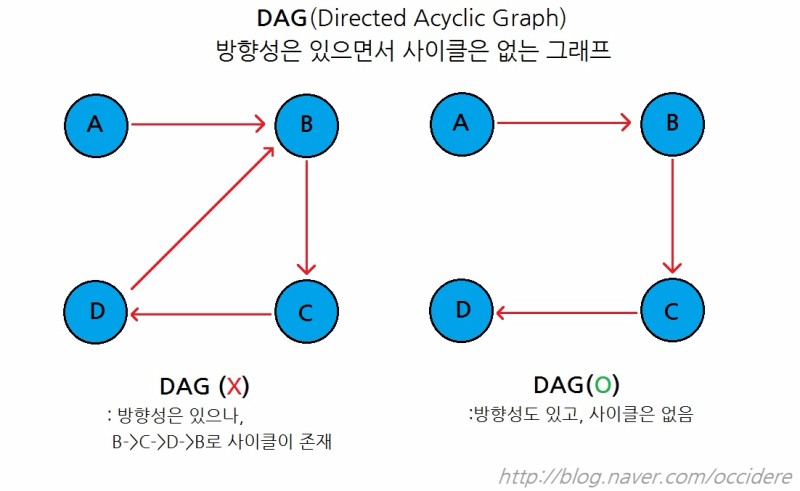
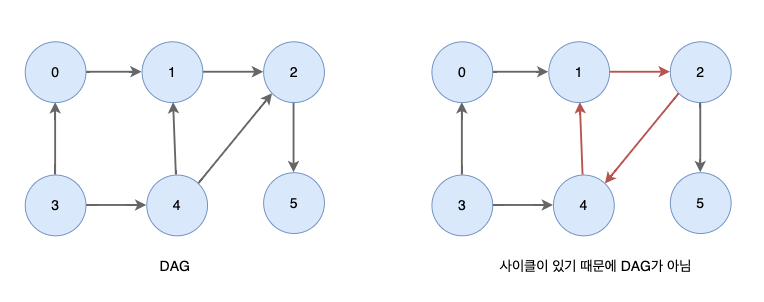
위상 정렬을 이해하기 위해서는 먼저 DAG를 알아야 한다.
DAG에서만 위상 정렬이 가능하다!
비순환 그래프(Directed Acyclic Graph)
- 사이클이 없는 (시작점에서 출발하면 다시 시작점으로 돌아올 수 없음)
- 유방향 그래프(간선은 한 방향으로만)
(우선순위를 나타내기 위해 주로 사용)
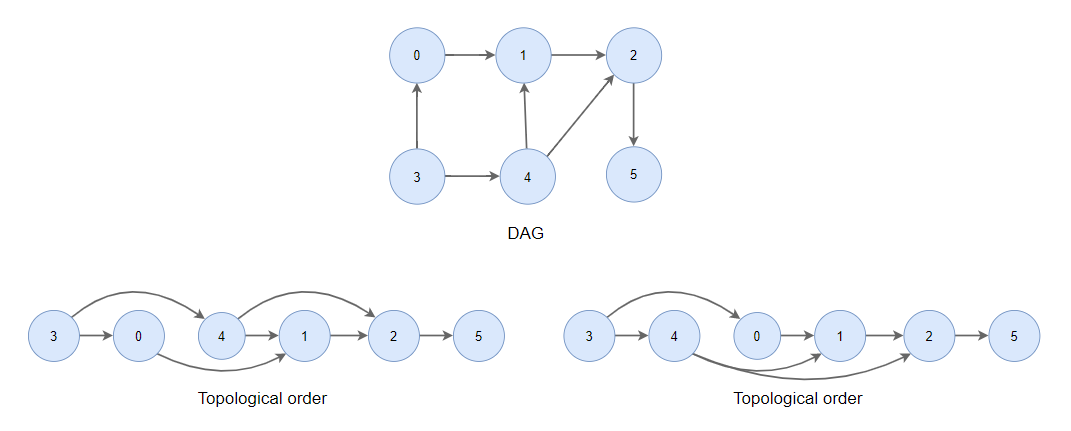
위상 정렬(topological sorting)이 뭐야?
유향 그래프의 꼭짓점을 변의 방향을 거스르지 않도록 나열하는 것
지금까지의 정렬은 '수'를 정렬하는 것이었다면 위상 정렬은 그래프를 정렬하는 것
진입 차수의 비 내림차순 순서로 정렬한다!
진입 차수: 각 노드로 들어오는 간선의 수
비 내림차순 순서: 비감소 순서, 동일한 값인 경우 상대적 순서가 중요하지 않음
진입차수가 동일한 경우 순서는 상관 없이 정렬한다!
즉 위상 정렬 결과는 여러 개가 나올 수 있다.
정렬 방법은 DFS를 이용하는 방법과 진입차수를 이용하는 방법(BFS)이 있다.
DFS탐색 결과를 역으로 하면 위상정렬과 같다.
위상 정렬 실행 방법
- 인접 리스트 형식으로 그래프 생성, 노드별 진입차수 기록
- 큐를 2개 생성
2.1 탐색 큐: 탐색할 노드를 저장
2.2 결과 큐: 정렬 결과를 저장 - 진입 차수가 0인 노드를 탐색 후 탐색 큐에 저장
(진입 차수가 0이면 정렬이 완료된 것!) - 탐색 큐에서 노드를 pull하고 결과 큐에 push
- 탐색 큐에서 뽑은 노드와 연결된 노드들의 진입차수를 -1
(직전 노드가 제거되어 다음 노드 입장에서는 진입차수가 1이 줄어들었기 때문) - 진입 차수 수정 결과가 0인 노드가 있으면 탐색 큐에 넣음.
4~6 과정을 탐색 큐가 빌 때까지 반복
최소 신장 트리를 구할 수 있는 알고리즘
- 크루스칼 알고리즘(Kruskal's Algorithm)
- 프림 알고리즘(Prim's Algorithm)
(MST) 1. 크루스칼 알고리즘(Kruskal's Algorithm)
특징
1. 간선의 가중치를 기준으로 MST를 구축하는 알고리즘
2. 초기에는 그래프의 모든 노드를 개별 트리로 간주
3. 간선들을 가중치 순으로 정렬, 가장 작은 가중치부터 간선부터 MST에 추가
(단, 사이클을 형성하는 간선은 무시)
4. 모든 노드가 MST에 포함될 때까지 '3'을 반복
그리디 알고리즘이다. 지금 당장 비용이 적은 것만 골라서 연결!
지금 가장 최선의 선택이 결과적으로 최선의 선택이다.
사이클을 형성하는 간선을 어떻게 찾지?
이때 필요한게 유니온(Union Find) 알고리즘
(이건 자료구조이기도 하다)
합집합 찾기 알고리즘 or 서로소 집합(Idsjoint-Set) 알고리즘
그래프에서 정점을 선택해서 그 정점이 서로 같은 그래프에 속하는지 판별
: 각 노드의 부모를 기록하고, 일반적으로 가장 작은 최상위 루트를 부모로 변경
같은 부모라면 같은 그래프로 판별
(처음 시작의 모든 부모는 자기 자신이다.)
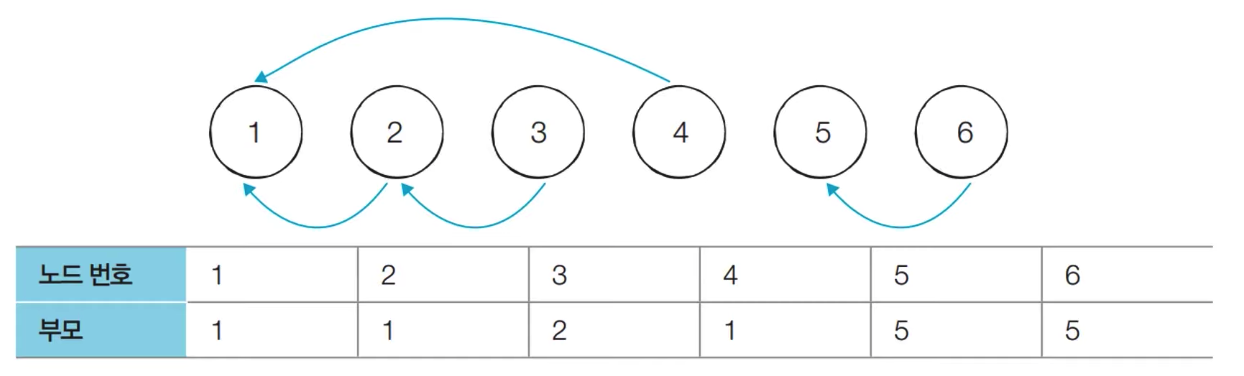
유니온 파인드(union find) 알고리즘
여러 노드가 존재할 때 어떤 두 개의 노드를 같은 집합으로 묶어 주고, 어떤 두 노드가 같은 집합에 있는지 확인하는 알고리즘
백준 11724 연결 요소의 개수 다시 풀기
그래프를 만들고 DFS로 탐색했는데, 유니온 파인드 문제인 것 같음!
import sys
# 유니온 파인드
def initialize(n):
parent = [i for i in range(n + 1)]
return parent
# 부모 노드 찾기
def find_root(node, parent):
if parent[node] == node:
return node
parent[node] = find_root(parent[node], parent)
return parent[node]
# 두 노드를 합치기
def union(node1, node2, parent):
root1 = find_root(node1, parent)
root2 = find_root(node2, parent)
if root1 != root2:
parent[root2] = root1
N, M = map(int, sys.stdin.readline().split())
edges = []
for _ in range(M):
u, v = map(int, sys.stdin.readline().split())
edges.append((u, v))
parent = initialize(N)
for u, v in edges:
union(u, v, parent)
conneted_components = len(set(find_root(node, parent) for node in range(1, N + 1)))
print(conneted_components)백준 문제 풀 때 그래프 문제라고 해서 무작정 그래프 구성하지 말고 해당 문제가 어떤 알고리즘의 케이스인지 확인하고 풀기!
아무리 봐도 모르겠음
마지막을len(set(parent[1: N + 1]))이렇게 하면 틀림
경로 압축
통과(경로 압축)
conneted_components = len(set(find_root(node, parent) for node in range(1, N + 1)))이건 중간중간 업데이트된 부모가 있기 때문에 때문에 재귀가 깊어지지 않음
리스트 슬라이싱은 빈 배열을 만들고 기존 배열을 참조하는데 메모리와 시간이 소요됨
리스트 컴프리헨션과 비슷하게 셋(set) 컴프리헨션도 있다!
백준 2606 바이러스 유니언 파인드로 풀어 봄
import sys
# 유니온 파인드
def init_parent(N):
parent = [i for i in range(0, N + 1)]
return parent
# 부모 노드 찾기
def find_root(node, parent):
if parent[node] == node:
return node
parent[node] = find_root(parent[node], parent)
return parent[node]
# 두 노드 합치기
def union(node1, node2, parent):
root1 = find_root(node1, parent)
root2 = find_root(node2, parent)
if root1 < root2:
parent[root2] = root1
elif root1 > root2:
parent[root1] = root2
N = int(sys.stdin.readline().strip())
M = int(sys.stdin.readline().strip())
edges = []
for _ in range(M):
u, v = map(int, sys.stdin.readline().strip().split())
edges.append((u, v))
parent = init_parent(N)
for edge in edges:
u, v = edge
union(u, v, parent)
result = [find_root(node, parent) for node in range(1, N + 1)]
print(result.count(1) - 1)마찬가지로 parent로 카운트하면 정답이 아님.. 왜 그런지 모르겠음
백준 2606 바이러스 DFS(재귀)로 풀어 봄!
이건 처음부터 끝까지 혼자 코딩함!
import sys
from collections import defaultdict
sys.setrecursionlimit(10**9)
N = int(sys.stdin.readline().strip())
M = int(sys.stdin.readline().strip())
edges = []
for _ in range(M):
u, v = map(int, sys.stdin.readline().strip().split())
edges.append((u, v))
graph = defaultdict(list)
for edge in edges:
u, v = edge
graph[u].append(v)
graph[v].append(u)
def dfs(v, graph, visited=None):
if visited is None:
visited = []
if v not in visited:
visited.append(v)
for w in graph[v]:
visited = dfs(w, graph, visited)
return visited
print(len(dfs(1, graph)) - 1)백준 2606 바이러스 DFS(반복)로 풀어 봄!
import sys
from collections import defaultdict
N = int(sys.stdin.readline().strip())
M = int(sys.stdin.readline().strip())
edges = []
for _ in range(M):
v, u = map(int, sys.stdin.readline().strip().split())
edges.append((v, u))
graph = defaultdict(list)
for edge in edges:
v, u = edge
graph[v].append(u)
graph[u].append(v)
def dfs_loop(start_v, graph, discovered=None):
if discovered is None:
discovered = []
stack = [start_v]
while stack:
v = stack.pop()
if v not in discovered:
discovered.append(v)
for w in graph[v]:
stack.append(w)
return discovered
print(len(dfs_loop(1, graph)) - 1)백준 2606 바이러스 BFS로 풀어 봄
import sys
from collections import deque, defaultdict
N = int(sys.stdin.readline().strip())
M = int(sys.stdin.readline().strip())
edges = []
for _ in range(M):
v, u = map(int, sys.stdin.readline().strip().split())
edges.append((v, u))
graph = defaultdict(list)
for edge in edges:
v, u = edge
graph[v].append(u)
graph[u].append(v)
def bfs(start_v, graph, discovered=None):
if discovered is None:
discovered = []
queue = deque([start_v])
while queue:
v = queue.popleft()
if v not in discovered:
discovered.append(v)
for w in graph[v]:
queue.append(w)
return discovered
print(len(bfs(1, graph)) - 1)
백준 2606 바이러스 4가지 방법으로 혼자 힘으로 풀었음!
유니언 파인드, DFS(재귀), DFS(반복), BFS는 기계적으로 타이핑 할 정도로 연습하자!
백준 5639 혼자 힘으로 다시 풀어 봄!
오.. 답지 안보고 혼자 풀어서 맞췄다. 재귀 조금 이해 됨.
(재귀는 맨날 이해만 하는 중)
근데 밤 되서 다시 보니까 또 모르겠네.
import sys
sys.setrecursionlimit(10 ** 9)
preorder = []
while True:
try:
preorder.append(int(sys.stdin.readline().strip()))
except:
break
def preorder_to_postorder(preorder):
postorder = []
if not preorder:
return postorder
root = preorder[0]
pointer = 1
while pointer < len(preorder) and preorder[pointer] < root:
pointer += 1
postorder.extend(preorder_to_postorder(preorder[1:pointer]))
postorder.extend(preorder_to_postorder(preorder[pointer:]))
postorder.append(root)
return postorder
postorder = preorder_to_postorder(preorder)
for node in postorder:
print(node)
백준 1260 BFS & DFS(재귀, 반복)
아래 코드 여러번 반복 타이핑해서 완전히 손에 익히기!
import sys
from collections import defaultdict, deque
sys.setrecursionlimit(10**6)
N, M, V = map(int, sys.stdin.readline().strip().split())
edges = []
for _ in range(M):
v, u = map(int, sys.stdin.readline().strip().split())
edges.append((v, u))
graph = defaultdict(list)
for edge in edges:
v, u = edge
graph[v].append(u)
graph[u].append(v)
def dfs_recursion(v, graph, discovered=None):
if discovered is None:
discovered = []
if v not in discovered:
discovered.append(v)
for w in sorted(graph[v]):
discovered = dfs_recursion(w, graph, discovered)
return discovered
def dfs_loop(start_v, graph, discovered=None):
if discovered is None:
discovered = []
stack = [start_v]
while stack:
v = stack.pop()
if v not in discovered:
discovered.append(v)
for w in sorted(graph[v], reverse=True):
stack.append(w)
return discovered
def bfs_loop(start_v, graph, discovered=None):
if discovered is None:
discovered = []
discovered.append(start_v)
queue = deque([start_v])
while queue:
v = queue.popleft()
for w in sorted(graph[v]):
if w not in discovered:
discovered.append(w)
queue.append(w)
return discovered
print(" ".join(map(str, dfs_loop(V, graph))))
print(" ".join(map(str, bfs_loop(V, graph))))이 문제는 DFS와 BFS의 가장 기본적인 문제.
여러번 따라쳐 보면서 익숙해지고, 코드를 정확히 이해하자!
파이썬 함수 가변객체
함수의 기본 인자가 함수가 정의될 때 한 번만 평가
가변 객체를 인자로 넘기는 함수는 부작용이 발생할 수 있다.
해당 객체가 동일 함수 반복 호출 시 계속 참조되기 때문임
# 예기치 않는 동작을 하는 코드
def add_to_list(value, default_list=[]):
default_list.append(value)
return default_list
print(add_to_list(1)) # 기대: [1], 결과: [1]
print(add_to_list(2)) # 기대: [2], 결과: [1, 2]
print(add_to_list(3)) # 기대: [3], 결과: [1, 2, 3]
# 개선 코드
def add_to_list(value, default_list=None):
if default_list is None:
default_list = []
default_list.append(value)
return default_list가변 객체(리스트, 딕셔너리, 집합 등)
파이썬 list vs set
list는 탐색 시 시간 복잡도가 O(n)이다.
set은 내부적으로 해시테이블로 구현되어 있어 시간 복잡도가 O(1)이다.
하지만 set은 순서가 보장되지 않는다.
백준 2178 미로 탐색 BFS
from collections import deque
# 좌, 우, 상, 하
dx = [-1, 1, 0, 0]
dy = [0, 0, -1, 1]
# (x, y)는 시작점, (n, m)은 도착점
def bfs(x, y, n, m, maze):
queue = deque()
queue.append((x - 1, y - 1))
while queue:
x, y = queue.popleft()
# '좌, 우, 상, 하'를 순서대로 탐색
for i in range(4):
nx = x + dx[i]
ny = y + dy[i]
# 미로 찾기 공간을 벗어난 경우 무시(진행 불가, 다른 큐 검색)
if nx < 0 or nx >= n or ny < 0 or ny >= m:
continue
# 벽인 경우 무시(진행 불가, 다른 큐 검색)
if maze[nx][ny] == 0:
continue
# 해당 노드 처음 방문 시 직전 노드의 값에서 1을 더한 값으로 변경
# 이동에 성공했으므로 다음 탐색할 인접 노드를 큐에 삽입
if maze[nx][ny] == 1:
maze[nx][ny] = maze[x][y] + 1
queue.append((nx, ny))
return maze[n - 1][m - 1]
# n행 m열
n, m = map(int, input().split())
maze = []
for _ in range(n):
maze.append(list(map(int, input())))
print(bfs(1, 1, n, m, maze))코드 이해는 됨. 2차원 배열 이해함. 비슷한 유형의 문제 풀어면 풀이 방법 체화될 듯!
여기서는 BFS로 좌, 우, 상, 하(순서는 바꿀 수 있음)인접 노드를 큐에 넣고,
다음 노드 진출 시 다음 노드의 인접 노드를 큐에 넣음.
큐는 선입선출 구조이기 때문에 뒤쪽에 누적되어도 출발지를 기준으로 인접 노드 부터 탐색함.
좌, 우, 상, 하와 같이 이 순서가 바뀌면 탐색 순서는 바뀔 수 있지만
각 노드별 거리 계산은 동일함!
크루스칼 알고리즘 hands on
pass(MST) 2. 프림 알고리즘(Prim's Algorithm)
특징
1. 시작 노드에서 출발해서 MST를 구축하는 알고리즘
2. 초기에는 시작 노드만 MST에 있음, 그래프의 모든 간선은 고려되지 않음
3. 각 단계에서 MST에 연결되지 않은 노드 중 최소 가중치 간선을 선택하여 MST에 추가
4. 모든 노드가 MST에 포함 될때까지 '3'을 반복
프림 알고리즘 hands on
pass
안녕하세요! 정글 5기 수강생입니다!!!
저도 유니언파인드로 마지막을 len(set(parent[1: N + 1]))이런식으로 하는데
출력은 잘 되는데 제출했다하면 틀리네요....
너무 답답해요ㅠ