일요일. 7시 50분에 강의실 옴
최소 신장 트리 맨날 못함.. 오늘은 한다!
알고리즘 이론은 이론 컴퓨터 과학의 하위 분야로 볼 수 있음.
최소 신장 트리를 구할 수 있는 알고리즘
- 크루스칼 알고리즘(Kruskal's Algorithm)
- 프림 알고리즘(Prim's Algorithm)
(MST) 1. 크루스칼 알고리즘(Kruskal's Algorithm)
특징
1. 간선의 가중치를 기준으로 MST를 구축하는 알고리즘
2. 초기에는 그래프의 모든 노드를 개별 트리로 간주
3. 간선들을 가중치 순으로 정렬, 가장 작은 가중치부터 간선부터 MST에 추가
(단, 사이클을 형성하는 간선은 무시)
4. 모든 노드가 MST에 포함될 때까지 '3'을 반복
유니온-파인드 간략 버전 hands on
크루스컬 알고리즘 공부하다가 최소 신장 트리는 순환 구조를 가지면 안 되는데 그걸 빠르게 판별할 수 있는 방법이 유니온 파인드!
재귀적으로 부모를 찾는다
(근데 유니온 파인드는 동일 집합 요소인지 판별하는 거니까 어느 쪽으로 일치시켜도 됨. 손으로 풀면서 증명함!)
def find(parent, x):
if parent[x] != x:
parent[x] = find(parent, parent[x])
return parent[x]
def union(parent, a, b):
a = find(parent, a)
b = find(parent, b)
if a < b:
parent[b] = a
else:
parent[a] = b
# 노드의 개수와 간선의 개수
v, e = map(int, input().split())
parent = [0] * (v + 1)
edges = []
# 부모 노드 초기화
for i in range(1, v + 1):
parent[i] = i
# 간선 정보 입력 받기
for _ in range(e):
a, b = map(int, input().split())
edges.append((a, b))
# 유니온 수행
for edge in edges:
a, b = edge
if find(parent, a) != find(parent, b):
union(parent, a, b)
# 각 노드의 대표자 찾기
roots = set()
for i in range(1, v + 1):
roots.add(find(parent, i))
# 연결된 그래프의 개수
connected_graphs = len(roots)
print(connected_graphs)
경로 압축
경로 모두를 표현하지 않고 주어진 로드와 루트 노드의 관계만 표현
경로가 중요하지 않고 같은 집합인지를 판별할 때 활용
경로 압축을 하면 경로 자체를 확인할 수는 없게 된다
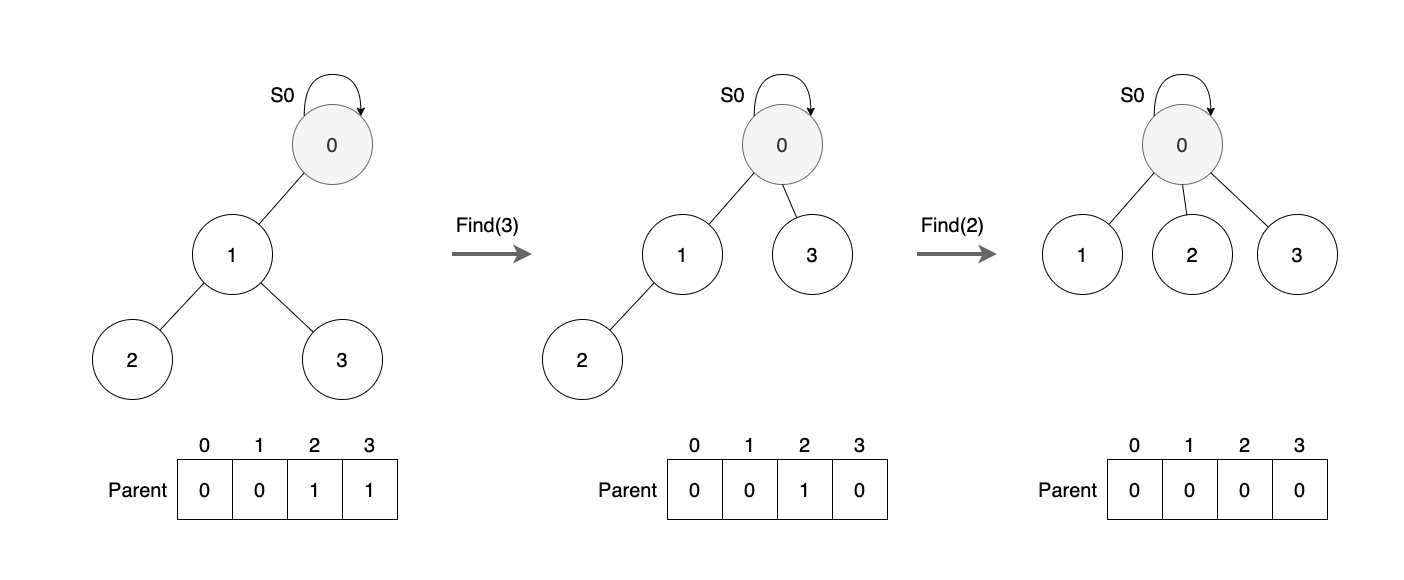
경로 압축은 노드와 루트 노드 사이의 중간 노드들을 건너뛰는 것!
백준 11724 연결 요소의 개수 유니온 파인드 재풀이
- 파인드 함수
- 유니온 함수
- 부모 배열
- 연결
- 부모 요소 파인드 함수로 set에 카운트
import sys
sys.setrecursionlimit(10 ** 6)
def find(v, parent):
if v != parent[v]:
parent[v] = find(parent[v], parent)
return parent[v]
def union(a, b, parent):
root1 = find(a, parent)
root2 = find(b, parent)
if root1 != root2:
parent[root2] = root1
N, M = map(int, sys.stdin.readline().strip().split())
edges = []
for _ in range(M):
u, v = map(int, sys.stdin.readline().strip().split())
edges.append((u, v))
parent = [i for i in range(N + 1)]
for edge in edges:
u, v = edge
union(u, v, parent)
parent_set = set()
for v in range(1, N + 1):
parent_set.add(find(v, parent))
print(len(parent_set))
유니온 파인드의 핵심은 각 그래프의 루트 노드를 연결하는 것!
이제 이 부분이 이해됨!if root1 != root2: parent[root2] = root1
유니온 파인드는 각 노드끼리 유니온 하는 게 아님. 각 노드의 루트 노드끼리 연결해서 경로가 분실되더라도 하나의 집합인지 아닌지만 판단
유니온 파인드의 핵심
유니온은 두 개의 집합을 합치는 함수이고 파인드는 각 집합의 대표 노드를 찾는 것!
즉, 대표 노드를 찾아서 두개를 연결시켜 줌
어떤 집합에서 대표 노드는 자기 자신이 대표 노드인 노드
DSU(disjoint set union) 자료구조를 클래스로 구현해 보았다
(유이온 파인드)
백준 11724 연결된 요소의 개수
import sys
sys.setrecursionlimit(10**6)
class DSU:
def __init__(self, size):
self.parent = [i for i in range(size + 1)]
def find_root(self, x):
if x != self.parent[x]:
self.parent[x] = self.find_root(self.parent[x])
return self.parent[x]
def union(self, x, y):
root_x = self.find_root(x)
root_y = self.find_root(y)
if root_x != root_y:
self.parent[root_y] = root_x
def is_same_set(self, x, y):
return self.find_root(x) == self.find(y)
def count_connected_component(self):
root = set()
for v in range(1, len(self.parent)):
root.add(self.find_root(v))
return len(root)
N, M = map(int, sys.stdin.readline().strip().split())
edges = []
for _ in range(M):
u, v = map(int, sys.stdin.readline().strip().split())
edges.append((u, v))
dsu = DSU(N)
for edge in edges:
u, v = edge
dsu.union(u, v)
print(dsu.count_connected_component())클래스로 자료구조를 구현하면 자료구조의 스키마가 머리 속에 잡히는 느낌!
크루스칼 알고리즘 hands on
import sys
sys.setrecursionlimit(10**6)
V, E = map(int, sys.stdin.readline().strip().split())
edges = []
for _ in range(E):
u, v, cost = map(int, sys.stdin.readline().strip().split())
edges.append((u, v, cost))
class DSU:
def __init__(self, N):
self.parent = [i for i in range(N + 1)]
def find_root(self, v):
if self.parent[v] != v:
self.parent[v] = self.find_root(self.parent[v])
return self.parent[v]
def union(self, v, u):
root_v = self.find_root(v)
root_u = self.find_root(u)
if root_v != root_u:
self.parent[root_u] = root_v
def is_same_root(self, v, u):
return self.find_root(v) == self.find_root(u)
dsu = DSU(V)
total_cost = 0
selected_edges = 0
sorted_edge = sorted(edges, key=lambda edge: edge[2])
for edge in sorted_edge:
v, u, cost = edge
if not dsu.is_same_root(v, u):
dsu.union(v, u)
total_cost += cost
selected_edges += 1
if selected_edges == V - 1:
break
print(total_cost)유니온 파인드는 알고리즘이 진행되는 과정에서는 각각 독립적인 트리로 존재하다가 최소 비용인 간선을 선택해나가면서 점진적으로 서로 연결되는 구조
(MST) 2. 프림 알고리즘(Prim's Algorithm)
특징
1. 시작 노드에서 출발해서 MST를 구축하는 알고리즘
2. 초기에는 시작 노드만 MST에 있음, 그래프의 모든 간선은 고려되지 않음
3. 각 단계에서 MST에 연결되지 않은 노드 중 최소 가중치 간선을 선택하여 MST에 추가
4. 모든 노드가 MST에 포함 될때까지 '3'을 반복
프림 알고리즘은 우선순위 큐를 주로 쓴다. 파이썬에서는 headpq를 쓰면 됨!
왜냐면 다음 인접 노드를 큐에 넣고, 그 중에서 가장 가중치가 작은 값을 꺼내야 하지 때문에 '최소힙'을 구현하는 파이썬 heapq를 활용하면 좋다!
파이썬 heapq 문법
# 힙큐 자체를 만드는 게 아님. 기존 리스트를 최소힙처럼 쓸 수 있음.
# 힙큐를 생성한다.
heap = []
# 힙큐에 추가하면서 히피파이를 수행한다.
heapq.heappush(heap, 5)
heapq.heappush(heap, 1)
heapq.heappush(heap, 9)
heapq.heappush(heap, 3)
# 가장 작은 값을 추출
print(heapq.heappop(heap))힙큐로 정렬하는 건 리스트가 정렬되는 게 아니다!
완전 이진 트리를 리스트로 나타내기 때문에 리스트의 정렬을 오름차순이 아닐 수 있지만, 힙큐를 통해 pop을 하면 최소값이 pop된다.
프림 알고리즘 hands on
import sys
import heapq
from collections import defaultdict
def prim(graph, start):
visited = set()
queue = [] # 큐
total_weight = 0
mst = []
heapq.heappush(queue, (0, start))
while queue:
weight, node = heapq.heappop(queue)
if node not in visited:
total_weight += weight
mst.append(node)
visited.add(node)
for adj_weight, adj_node in graph[node]:
if adj_node not in visited:
heapq.heappush(queue, (adj_weight, adj_node))
return total_weight
V, E = map(int, sys.stdin.readline().strip().split())
edges = []
for _ in range(E):
v, u, weight = map(int, sys.stdin.readline().strip().split())
edges.append((v, u, weight))
graph = defaultdict(list)
for edge in edges:
v, u, weight = edge
graph[v].append((weight, u))
graph[u].append((weight, v))
print(prim(graph, 1))프림 알고리즘은 BFS와 비슷하게 하나의 노드에서 인접 노드 중에 최선의 노드를 선택해 나가는 방식
큐에 넣을 때는 (가중치, 노드) 순으로 넣어야 함! heapq는 튜플의 경우 첫 번째 값을 기준으로 (최소)히피파이를 수행하기 때문!
Git
빨래 기다리면서 김코치님이 알려주신 브랜치 사이트 연습해 봄
branch
브랜치는 단지 특정 커밋을 가리키는 참조이다
브랜치를 자주 만들고 사용해도 메모리에 부담이 되지 않는다.
작업을 작은 단위의 브랜치로 만들어라.
# 브랜치 만들기
git branch {브랜치명}
# 현재 브랜치 바꾸기
git swtich {브랜치명}
# checkout 대신 여러 명령어로 분화됨브랜치는 하나의 커밋과 그 부모 커밋들을 포함하는 작업 내역
결국에 브랜치는 하나의 커밋을 가리킨다!
merge
두 개의 부모를 가리키는 커밋을 만드는 것
# 현재 브랜치로 새로운 브랜치를 가지고와서 머지
git merge {가지고 올 브랜치}rebase
커밋들을 모아서 복사한 뒤 다른 곳에 떨구는 것
커밋의 흐름을 한 줄로 만들 수 있다.
git rebase {최종적으로 재배치할 브랜치(대상 브랜치)}head
체크아웃된 커밋을 가리킨다(= 현재 작업 중인 커밋을 가리킨다)
엄밀히 말하면 일반적으로는 브랜치가 커밋을 가리키고, 헤드가 브랜치를 가리키는 구조
(커밋 <- 브랜치 <- 헤드)
일반적으로 head는 브랜치 이름을 가리킨다.
헤드를 분리하면 브랜치가 아니라 커밋을 직접 가리킬 수도 있다.
(각각의 커밋을 해시값으로 구분할 수 있다.)
git switch {커밋 해시값}상대 참조
^: 한 번에 한 커밋 위(부모)로 움직인다
git switch main^
git switch main^^
~num: 한 번에 여러 커밋 위로 올라간다
git switch head~4
브랜치 강제로 옮기기
-f 옵션으로 특정 커밋에 브랜치를 직접적으로 재지정할 수 있다.
git branch -f main HEAD~3
git 작업 되돌리기
1. reset
브랜치가 예전 커밋을 가리키도록 이동시키는 방식
애초에 커밋하지 않은 것처럼 이전 커밋으로 이동(커밋 히스토리가 변경)
히스토리를 고쳐 쓰기 때문에 리모트 브랜치에서는 사용 불가
git reset HEAD~1
2. revert
되돌리고자 하는 내용으로 새로운 커밋을 생성
커밋 히스토리가 추가만 됨
HEAD 커밋의 변경사항을 되돌리는(반대되는 내용) 새로운 커밋을 생성
git revert HEADcherry-pick
HEAD 다음에 커밋들을 대한 복사본을 만든다.
특정 커밋들만 골라서 현재 HEAD 밑으로 복사해서 붙인다.
git cherry-pick {커밋} {커밋} ...
rebase -i
인터렉티스 리베이스
커밋 히스토리를 직접 조작할 수 있음!
리베이스의 목적지가 되는 곳 아래에 복사된 커밋들을 보여줌
git rebase -i {재배치가 시작될 기준 커밋}
DFS vs BFS 개선
현재 내가 짠 코드는 해당 노드 방문 여부를 체크할 때 이미 완성된 결과에서 노드가 있는지 탐색한다.
def dfs(v, graph, visited=None):
if visited is None:
visited = []
if v not in visited:
visited.append(v)
for w in graph[v]:
visited = dfs(w, graph, visited)
return visited하지만 이 방식은 리스트에 해당 요소가 있는지 없는지를 찾을 때는 시간 복잡도가 O(n)이 걸린다. 이걸 해결하려면 2가지 방법이 있다.
1. [False] * n 인 리스트를 만들어서 방문하면 인덱스로 방문했다고 처리하는 것
2. set()을 만든 수 add로 방문한 노드를 추가하는 방법
1은 직관적으로 처리할 수 있지만 노드명이 숫자인 경우에만 사용할 수 있다.
2는 직관적이지 않지만 다양한 노트 타입에 대응할 수 있는 장점이 있다.
두 가지를 모두 사용할 수 있어야 한다!
탐색 알고리즘 복습
이미 푼 문제 혼자 힘으로 풀 수 있을 때까지 반복 연습!
1191 트리 순회
결과를 extend하는 것보다 리스트 참조값을 넘겨서 더 깔끔하게 구현 성공!
import sys
def preorder(tree, node, order=None):
if order is None:
order = []
if node:
left, right = tree[node]
order.append(node)
preorder(tree, left, order)
preorder(tree, right, order)
return order
def inorder(tree, node, order=None):
if order is None:
order = []
if node:
left, right = tree[node]
inorder(tree, left, order)
order.append(node)
inorder(tree, right, order)
return order
def postorder(tree, node, order=None):
if order is None:
order = []
if node:
left, right = tree[node]
postorder(tree, left, order)
postorder(tree, right, order)
order.append(node)
return order
N = int(sys.stdin.readline().strip())
nodes = []
tree = {}
for _ in range(N):
root, left, right = sys.stdin.readline().strip().split()
if left == ".":
left = None
if right == ".":
right = None
tree[root] = (left, right)
print("".join(preorder(tree, "A")))
print("".join(inorder(tree, "A")))
print("".join(postorder(tree, "A")))
5639 이진 검색 트리
전체적인 로직은 혼자 구현!
일부 오류를 GPT 도움 받음
함수명과 파라미터명을 동일하게 해서 오류 발생
(함수명 바꾸자 해결됨)
import sys
sys.setrecursionlimit(10 ** 6)
preorder = []
while True:
try:
node = int(sys.stdin.readline().strip())
preorder.append(node)
except:
break
def postorder_recursion(preorder, postorder=None):
if postorder is None:
postorder = []
if not preorder:
root = preorder[0]
i = 1
while i < len(preorder):
if preorder[i] > root:
break
i += 1
postorder_recursion(preorder[1:i], postorder)
postorder_recursion(preorder[i:], postorder)
postorder.append(root)
return postorder
for node in postorder_recursion(preorder):
print(node)리스트에 요소가 있는지 검사할 때는 len 보다 아래 코드가 더 깔끔
파이썬은 빈 요소를 False로 평가함
# 내가 쓴 코드
if len(preorder) > 0:
# 개선 코드
if preorder:1260 DFS & BFS
파이썬 deque는 collections이고
heapq는 그 자체다.
from collections import deque
import heapqDFS(재귀), DFS(반복), BFS(반복)을 혼자 힘으로 구현했음!!!!
코드도 이해되고 혼자 작성도 가능함!!!
잊어 버리지 않게 자주 복습하고 이제 응용 문제 풀어봐야겠음!!!
import sys
from collections import defaultdict, deque
sys.setrecursionlimit(10**6)
N, M, V = map(int, sys.stdin.readline().strip().split())
edges = []
for _ in range(M):
v, u = map(int, sys.stdin.readline().strip().split())
edges.append((v, u))
graph = defaultdict(list)
for edge in edges:
v, u = edge
graph[v].append(u)
graph[u].append(v)
def dfs_recursion(graph, node, order=None, visited=None):
if order is None:
order = []
if visited is None:
visited = set()
if node not in visited:
order.append(node)
visited.add(node)
for adj_node in sorted(graph[node]):
dfs_recursion(graph, adj_node, order, visited)
return order
def dfs_loop(graph, start_v):
order = []
visited = set()
stack = []
stack.append(start_v)
while stack:
node = stack.pop()
if node not in visited:
order.append(node)
visited.add(node)
for adj_node in sorted(graph[node], reverse=True):
stack.append(adj_node)
return order
def bfs_loop(graph, start_v):
order = []
visited = set()
queue = deque()
queue.append(start_v)
while queue:
node = queue.popleft()
if node not in visited:
order.append(node)
visited.add(node)
for adj_node in sorted(graph[node]):
queue.append(adj_node)
return order
# print(dfs_recursion(graph, V))
print(" ".join(map(str, dfs_loop(graph, V))))
print(" ".join(map(str, bfs_loop(graph, V))))
백준 11724 연결 요소의 개수 다시 풀어봄
와.. 이게 되는구나. 여러 번 연습하니까 혼자서도 짤 수 있게 됨!
코드를 그냥 외우는게 아니라 이해하고 다시 작성할 수 있게 됨!
유니온 파인드
import sys
from collections import defaultdict
sys.setrecursionlimit(10**6)
class DSU:
def __init__(self, N: int) -> None:
self.parent = [i for i in range(N + 1)]
self.N = N
self.graph = None
def set_graph(self, graph: defaultdict) -> None:
self.graph = graph
def find_root(self, node: int) -> int:
if self.parent[node] != node:
self.parent[node] = self.find_root(self.parent[node])
return self.parent[node]
def union(self, u: int, v: int) -> None:
root_u = self.find_root(u)
root_v = self.find_root(v)
if root_u != root_v:
self.parent[root_v] = root_u
def connetcted_component(self) -> int:
return len(set(self.find_root(i) for i in range(1, self.N + 1)))
N, M = map(int, sys.stdin.readline().strip().split())
edges = []
for _ in range(M):
u, v = map(int, sys.stdin.readline().strip().split())
edges.append((u, v))
graph = defaultdict(list)
for edge in edges:
u, v = edge
graph[u].append(v)
graph[v].append(u)
dsu = DSU(N)
dsu.set_graph(graph)
for edge in edges:
u, v = edge
dsu.union(u, v)
print(dsu.connetcted_component())백준 2606 바이러스 다시 풀어 봄
재귀 함수라고해서 반복문을 쓰지 않는 건 아니다.
재귀 함수를 스스로를 호출하는 함수이며,
그 안에서 조건문, 반복문 등 로직은 다양하게 사용될 수 있다.
GPT 도움 안 받고 혼자서 DFS(재귀, 반복), BFS 모두 구현 성공!
import sys
from collections import defaultdict, deque
sys.setrecursionlimit(10**6)
def dfs_recursion(node, graph, order=None, visited=None):
if order is None:
order = []
if visited is None:
visited = set()
if node not in visited:
order.append(node)
for adj_node in graph[node]:
dfs_recursion(adj_node, graph, order, visited)
return order
def dfs_loop(start_v, graph, order=None, visited=None):
if order is None:
order = []
if visited is None:
visited = set()
stack = []
stack.append(start_v)
while stack:
node = stack.pop()
if node not in visited:
order.append(node)
visited.add(node)
for adj_node in graph[node]:
stack.append(adj_node)
return order
def bfs_loop(start_v, graph, order=None, visited=None):
if order is None:
order = []
if visited is None:
visited = set()
queue = deque()
queue.append(start_v)
while queue:
node = queue.popleft()
if node not in visited:
order.append(node)
visited.add(node)
for adj_node in graph[node]:
queue.append(adj_node)
return order
N = int(sys.stdin.readline().strip())
M = int(sys.stdin.readline().strip())
edges = []
for _ in range(M):
u, v = map(int, sys.stdin.readline().strip().split())
edges.append((u, v))
graph = defaultdict(list)
for edge in edges:
u, v = edge
graph[u].append(v)
graph[v].append(u)
# print(len(dfs_recursion(1, graph)) - 1)
# print(len(dfs_loop(1, graph)) - 1)
print(len(bfs_loop(1, graph)) - 1)오.. 이제 혼자서도 뭔가 풀린다.
DFS, BFS 이제 개념 잡혔음! 응용 문제 많이 풀어보기!
백준 1197 최소 스패닝 트리 복습!
크루스칼과 프림으로 풀어 봄
최소 신장 트리에서 간선의 개수는 노드 - 1 기억하기!
최소 신장 트리 알고리즘은 아직 완전히 혼자서는 구현 어려움.
크루스칼 알고리즘: DSU, heapq, 간선 = 정점 - 1 기억하기
import sys
import heapq
from collections import defaultdict
class DSU:
def __init__(self, N):
self.parents = [i for i in range(N + 1)]
def find_root(self, node):
if self.parents[node] != node:
self.parents[node] = self.find_root(self.parents[node])
return self.parents[node]
def union(self, u, v):
root_u = self.find_root(u)
root_v = self.find_root(v)
self.parents[root_v] = root_u
V, E = map(int, sys.stdin.readline().strip().split())
edges = []
for _ in range(E):
u, v, weight = map(int, sys.stdin.readline().strip().split())
edges.append((u, v, weight))
dsu = DSU(V)
queue = []
for edge in edges:
u, v, weight = edge
heapq.heappush(queue, (weight, u, v))
mst_edges = []
while len(mst_edges) < V - 1:
weight, u, v = heapq.heappop(queue)
if dsu.find_root(u) != dsu.find_root(v):
dsu.union(u, v)
mst_edges.append((weight, u, v))
total_weight = 0
for edge in mst_edges:
weight, u, v = edge
total_weight += weight
print(total_weight)오류 복기
DSU에서 간선 연결을 미리 다 해버렸음. 그러면 쓸데가 없음.
크루스칼 알고리즘에서 각 간선을 체크하고, 순환하지 않으면 그때 DSU의 그래프를 연결(유니언)하기!
프림 알고리즘
프림도 힙큐(우선순위큐)를 쓴다.
크루스칼은 우선 모든 간선을 다 집어넣고 꺼내는 반면에
프림은 방문한 노드의 인접 노드만 힙큐에 집어넣는다.
프림 알고리즘은 BFS와 비슷한 로직으로 진행된다.
프림 알고리즘: heapq
import sys
from collections import defaultdict
import heapq
V, E = map(int, sys.stdin.readline().strip().split())
edges = []
for _ in range(E):
u, v, weight = map(int, sys.stdin.readline().strip().split())
edges.append((u, v, weight))
graph = defaultdict(list)
for edge in edges:
v, u, weight = edge
graph[v].append((weight, u))
graph[u].append((weight, v))
def prim(graph, start_v):
visited = set()
mst = []
queue = []
heapq.heappush(queue, (0, start_v))
while len(visited) < V:
weight, node = heapq.heappop(queue)
if node not in visited:
mst.append((weight, node))
visited.add(node)
for weight, adj_node in graph[node]:
heapq.heappush(queue, (weight, adj_node))
return mst
mst = prim(graph, 1)
total_weight = 0
for weight, _ in mst:
total_weight += weight
print(total_weight)오류 복기
heapq 쓰는 것 익숙하지 않아서 오류 많이 발생함.
heaqp는 리트스에 데이터를 넣을 때 히피파이를 할 수 있다.
데이터를 넣을 때:heapq.heappush(리스트명, 데이터)
데이터를 꺼낼 때:heapq.heappop(리스트명)
리스트명을 빼먹어서 자꾸 틀림. 히피파이를 수행할 리스트를 지정해줘야 함!
크루스컬 vs 프림
크루스컬을 while문에서while len(mst_edges) < V - 1:이렇게 돌리는데
프림은while len(mst) < V:이렇게 돌림. 왜?
크루스컬은 간선 중심 알고리즘이고, 프림은 노드 중심 알고리즘이다!
