[계산사진학] Image Filtering - Image Gradients and Edge Detection

JAEYOON SIM·2021년 10월 4일

Computational Photography

목록 보기

7/34

Gradients

Gradient는 각 변수들의 1차 미분한 결과을 모아놓은 것을 말한다.

\nabla f(x,y)=\begin{bmatrix}\frac{\partial f(x,y)}{\partial x}\\\frac{\partial f(x,y)}{\partial y}\end{bmatrix}

이미지를 (x, y)라는 함수로 생각을 했을 때, (x, y)에서의 f(x, y)라는 함수값은 intensity value가 된다. 그러면 우리는 이미지에서의 gardient를 위와 같이 정의할 수 있다. 하지만, 문제는 이미지는 discrete한 값들로 구성이 되어 있기 때문에 continuous하지 않다. 그러면 위의 식을 정의를 한다고 했을 때, 어떻게 계산을 해야할까?

바로 finite한 difference를 이용해서 미분의 결과를 approximate하면 된다. 만약 continuous function을 사용하여 미분을 하게 되면 다음과 같이 limit를 사용하면 된다.

\frac{\partial f(x,y)}{\partial x}=\lim_{x \to 0}\frac{f(x+h, y)-f(x,y)}{h}

하지만 이미지에서의 gradient를 구하기 위해서는 위와 같이 구할 수는 없다. 그래서 finite하게 다음과 같이 3가지 식으로 구할 수 있다.

1. Forward finite difference

\frac{\partial f(x,y)}{\partial x}=\frac{f(x+h, y)-f(x,y)}{h}\Rightarrow f(x+1,y)-f(x,y) \quad when\; h=1

2. Backward finite difference

\frac{\partial f(x,y)}{\partial x}=f(x,y)-f(x-1,y)

3. Central finite difference

\frac{\partial f(x,y)}{\partial x}=\frac{f(x+1,y)-f(x-1,y)}{2}

그리고 이렇게 finite difference를 계산하는 과정은 convolution operation을 이용해서 이미지에 적용이 된다.

1. Forward finite difference

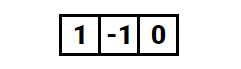
2. Backward finite difference

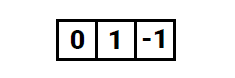
3. Central finite difference

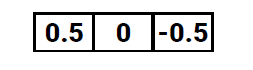
Sobel Filter

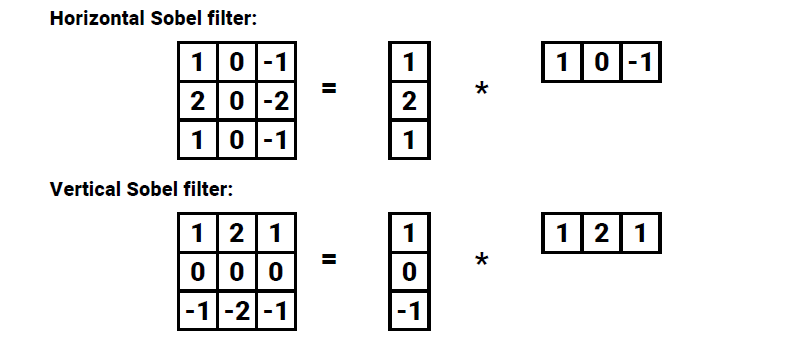
이미지나 영상으로부터 edge를 검출하는 것이 목표이며, edge를 검출하는 filter 중에서 가장 기본이 되는 것이 sobel filter이다. 우리는 x축의 수평 방향과 y축의 수직 방향으로 미분할 수가 있다. 그렇기 때문에 sobel filter 또한 2종류가 필요하게 된다.
다음은 sobel filter를 사용한 예시다.
Horizontal sobel filter를 사용하면 대체적으로 많은 vertical line을 얻을 수가 있다. 반대로 vertical sobel filter를 사용하게 되면 많은 horizontal line을 얻게 된다. 또 다른 예시도 살펴보자.
Horizontal sobel filter같은 경우 중심을 기준으로 수직 방향으로 component 값이 0이다. 그렇기 때문에 이를 이미지에 사용하게 되면 vertical line이 검출이 된다.

Computing Gradients

그래서 이미지에 gradient를 계산하는 과정을 정리해보면 우선 이미지에 사용 할 적절한 derivative filter를 선택해야 한다. Sobel filter를 선택했다고 생각하고 다음으로는 이filter를 이용해서 convolution 연산을 이미지와 진행해서 derivative를 계산해준다. 그렇게 해서 이미지 gradient를 만들게 되면 이를 이용해서 direction이나 amplitude도 원하는대로 계산이 가능해진다.
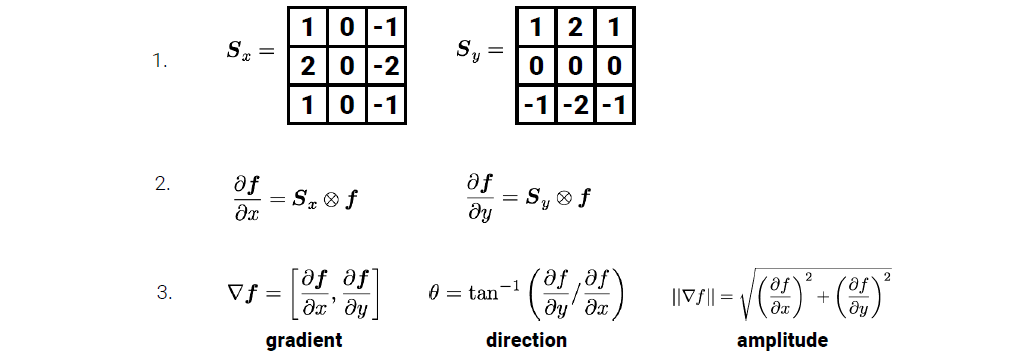그렇게 해서 convolution을 진행한 결과가 다음과 같다.
여기서 중요한 것은 어떻게 gradient의 방향이 edge와 관련이 있는지이다. 이미지 상에서 direction을 따라서 픽셀 값은 대부분 상당한 영향을 받게 된다. 그래서 edge direction은 항상 gradient direction과 수직 관계에 놓이게 된다.

How to Find Edges

Gradient를 계산하는 것은 edge를 검출하는 것과 같다는 결론에 도달했다. 그러면 다음의 signal로부터 edge를 검출해보려고 한다.
우리가 원하는 것은 intensity가 크게 변하는 지점을 찾고싶다. 이미 derivative를 계산하는 방법은 알고 있다. 그럼 이제 derivative filter를 이용해서 edge를 찾아볼 것이다. 다음은 derivative filter를 이용한 결과이다.
하지만 문제가 생겼다. Filtering한 결과로부터 intensity가 크게 변하는 지점을 찾을 방법이 없다. 굉장히 high frequency에다가 edge가 어디인지 알 수가 없어졌다. 그 이유는 원래 input signal 자체가 noise가 굉장히 많기 때문이다.

Differentiation은 noise에 굉장히 민감하게 작용한다. 그렇기 때문에 derivative filter를 사용해서 edge를 검출하기 위해서는 조금 다른 방법이 필요하다. Input signal로부터 noise를 제거해주는 작업이 필요하다. 즉, high frequency component를 제거해야 하는데, 이는 Gaussian filter를 이용하면 가능해진다.
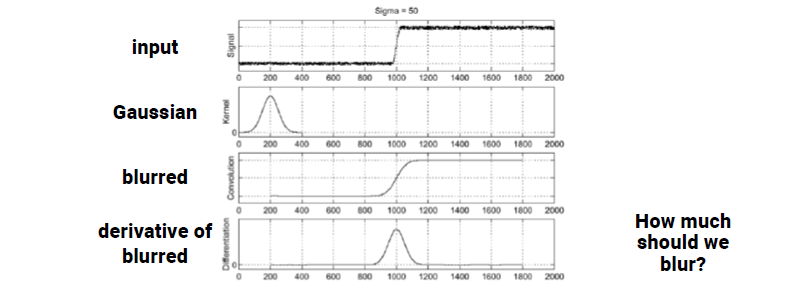Gaussian filter를 이용한 결과를 보면 noise가 보이지 않게 된다. Blur 처리가 된 이미지 상에서 derivative filter를 사용할 것이다. 그래서 Gaussian filter를 적용한 뒤에 derivative filter를 적용하게되면 input signal 상에서 intensity가 크게 변하는 지점을 쉽게 발견할 수 있다. 그 결과 우리는 edge를 검출할 수 있다. 그러면 어느정도로 blur 처리를 해야 할까? 이는 input에 대해서 noise의 양이 어느정도인지에 따라 다르다. 이는 상황에 따라 적절하게 대처를 해야 한다.

Derivative of Gaussian(DoG) Filter

그래서 위와 같은 과정을 한번에 진행하기 위해서 derivative of Gaussian(DoG) filter라는 것에 대해서 알아보려고 한다.

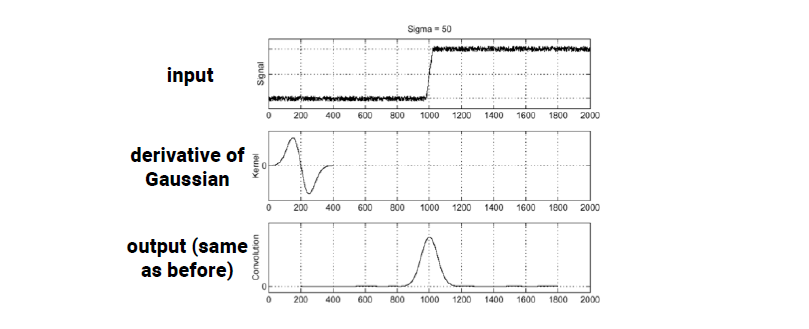\frac{\partial}{\partial x}(h * f) = (\frac{\partial}{\partial x}h) * f

이전에 Gaussian filter를 적용하고 derivative filter를 적용한 결과와 DoG filter를 적용한 결과가 같음을 볼 수 있다. 이 filter를 사용하게 되면 computational cost를 줄일 수가 있다. Filter를 2개 사용하는데 filter간의 연산은 상대적으로 작은 크기의 연산이기 때문에 연산량에서 효율적이다.

Laplacian of Gaussian(LoG) Filter

Laplacian of Gaussian(LoG) filter를 알아보기 전에 laplace filter에 대해서 알아보려고 한다. Laplace filter는 기본적으로 2차 미분을 사용한 filter이다.
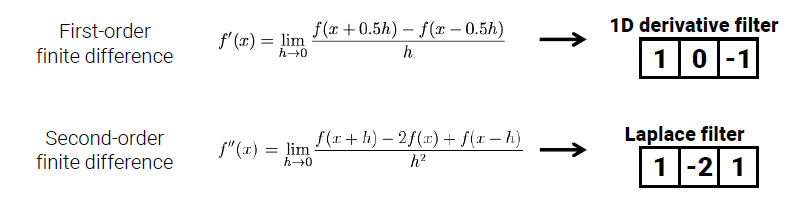그러면 이 laplace filter를 이용한 LoG filter에 대해서 다음의 signal을 살펴보자.
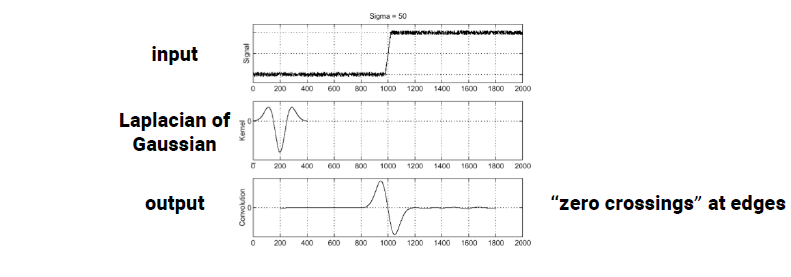이번에도 우리가 원하는 것은 input signal로부터 intensity가 크게 변하는 지점을 찾아서 edge를 검출하는 것이다. LoG filter를 사용하면 같은 지점에서 변화가 발생한 것을 볼 수 있는데, Dog filter와는 특징이 다르게 나타난다. LoG filter를 사용하면 edge인 지점을 기준으로 값의 변화가 있고, 해당 지점의 값은 0이 되는 것을 볼 수 있다. 우리는 이를 zero crossing이라고 부르며, 이는 LoG filter를 이용해서 edge를 검출하는 방법이다.

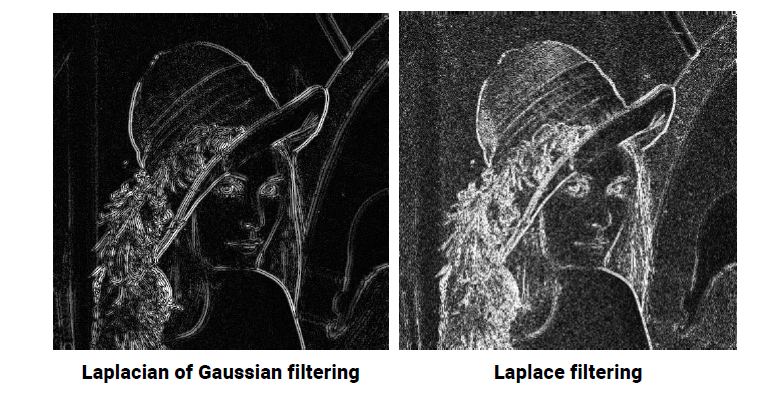
다음은 laplace filter와 LoG filter를 사용한 결과를 비교한 것인데, laplace filtering을 진행하게 되면 noise가 굉장히 많이 발생해서 edge를 검출하기 어려운 것을 알 수가 있다. 반면에, LoG filtering은 더 깔끔한 결과를 만들어낸다.

LoG vs. DoG

그러면 이제 LoG filtering과 DoG filtering을 비교해보려고 한다.
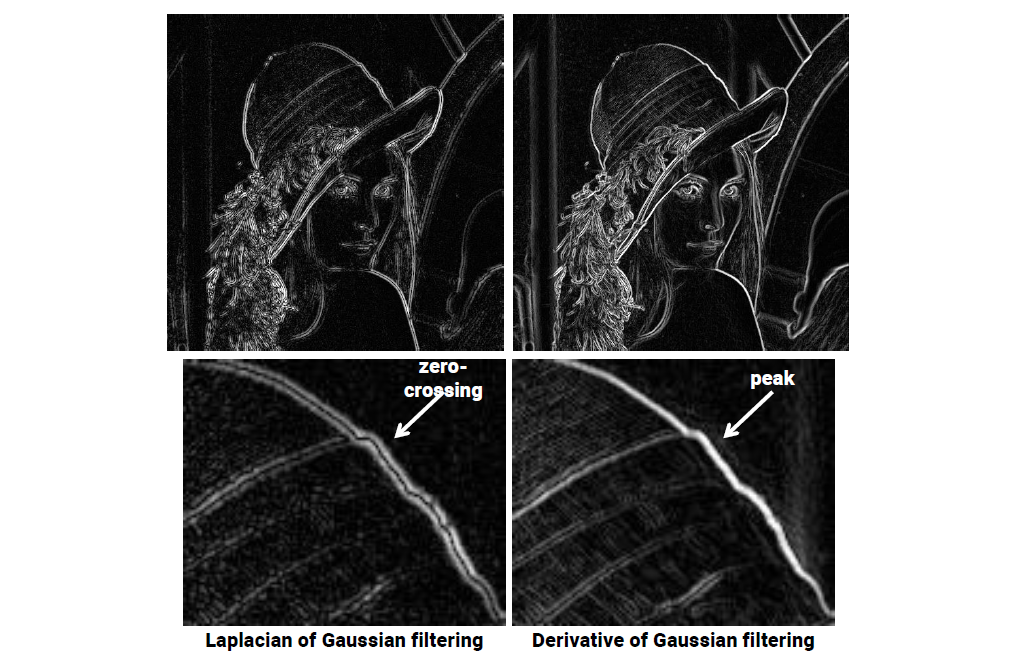LoG filtering 결과 line이 이중으로 검출되는 것을 볼 수가 있다. 이는 zero crossing에 의하여 생긴 결과로, DoG filtering 보다 좀 더 정확하게 결과를 낼 수가 있다. 그렇다고 하더라고 LoG filter를 사용하는 것이 DoG filter를 사용하는 것보다 더 적절하다고 판단할 수는 없다. 상황에 따른 결과가 달라지기 때문에 두 방법을 이용해서 edge를 검출할 수 있다는 사실을 알고 있으면 된다.

Image Boundary Problem

Convolution 연산을 진행할 때 문제점이 무엇이었는가? 바로 이미지 외곽 부분의 처리였다. Filter를 이미지에 적용해서 window를 하고 계산을 할 때, 외곽의 모서리 부분은 convolution 연산의 영향을 받지 못한다. 그래서 외곽의 픽셀 값을 만들 필요성이 생긴다. 이를 해결하기 위한 몇가지 방법을 알아보려고 한다. 단, 이 방법들이 전부 효과적이라고 말할 수는 없다.

Clip filter(black): 이 방법은 이미지의 테두리를 따라서 검은색의 테두리를 추가해서 convolution을 진행하는 것이다. 이렇게 되면 문제점이 만약에 밝은 하늘 이미지를 대상으로 진행했을 때, 하늘색이 보존이 되지 않고 어두워질 수가 있다. 그래서 이 방법은 좋은 결과를 가져오지 못한다.
Wrap around: 이 방법은 원본 이미지를 두고 상하좌우 그리고 대각 방향까지 같은 사진을 붙여놓고 convolution을 진행하는 것이다.
Copy edge: 이 방법은 외곽 모서리의 부분을 그대로 복사해서 이미지 주변을 두르고 convolution을 진행하는 것이다.
Reflect across edge: 이 방법은 원본 이미지를 기준으로 좌우대칭하여 좌측과 우측에 이어붙이고, 상하대칭하여 위와 아래에 이어붙여서 convolution을 진행하는 것이다.
Vary filter near edge

JAEYOON SIM

평범한 공대생의 일상 (글을 잘 못 쓰는 사람이라 열심히 쓰려고 노력 중입니다^^)