[시각지능] Detecting corners

Detecting corners

이번에는 영상에서 corner를 찾아보고 왜 corner가 중요한지에 대해서 알아보고자 한다. 영상에서 corner을 왜 찾아야만 하는 것일까? 이번부터는 영상과 영상 사이의 관계성에 대해서 알아볼 것이며 여기서 corner가 굉장히 중요한 역할을 하게 된다. 우리가 corner를 찾게되면 이로부터 굉장히 다양한 task를 수행할 수 있게 된다. Image alignment, 3D reconstruction, motion tracking, object recognition 등에서 corner는 중요한 역할을 한다. 이러한 task들의 특징은 corner를 기준으로 위치를 추정하거나 찾을 수가 있기 때문이다.

Corner를 찾기 위해서 먼저 corresponding point에 대해서 알아보려고 한다. Corresponding point는 2개의 image에서 물리적으로 어느 지점이 대응되는지를 의미한다. 양쪽 image에서 대응되는 지점을 찾아야 하며, 이는 사람의 눈으로 찾고자 한다면 다소 어려울 수 있다. 이는 사람보다 컴퓨터가 훨씬 잘하는 일이다. Corresponding point를 찾기 위해서 시작하는 지점이 바로 corner이다.

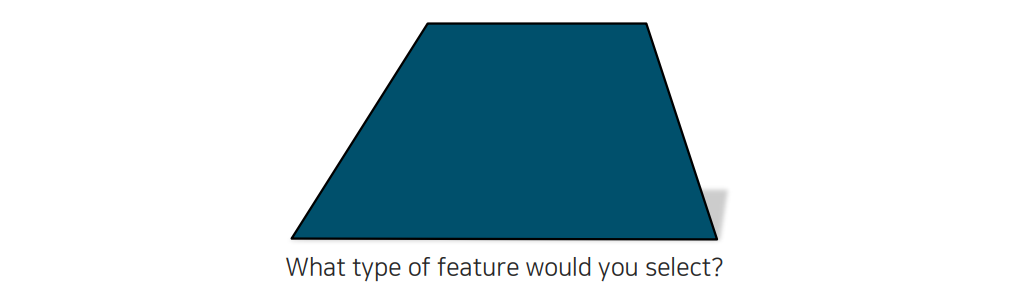위의 도형에서 한가운데에 점을 찍고 그 근방을 살펴본다고 해보자.
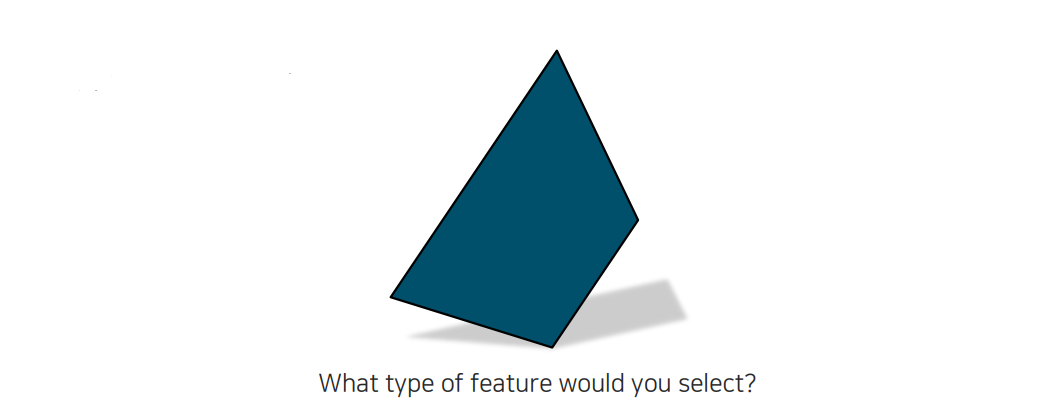그리고 동일한 점을 위의 도형에서 찾는다고 해보자. 아마 완전히 똑같은 지점을 찾는 것은 불가능할 것이다. 하지만 우리가 corner point를 찾는다고 한다면 도형이 어떻게 움직여도 쉽게 찾을 수 있을 것이다. 이렇게 corner는 도형이 움직여도 쉽게 찾아낼 수 있는 특징이 되는 것이다. 도형에서 edge도 있지만 도형이 움직이게 된다면 이 또한 찾기 어려울 것이다. Corner point 부분은 대응점을 찾는 것이 굉장히 용이하기 때문에 이를 기준으로 다른 task를 하는 것이 매우 편할 것이다.

Harris corner detector

Corner는 image에서 point와 point 사이의 관계를 나타내는데 있어 굉장히 중요한데, 이를 찾는 대표적인 알고리즘인 Harris corner detector에 대해서 알아보려고 한다.
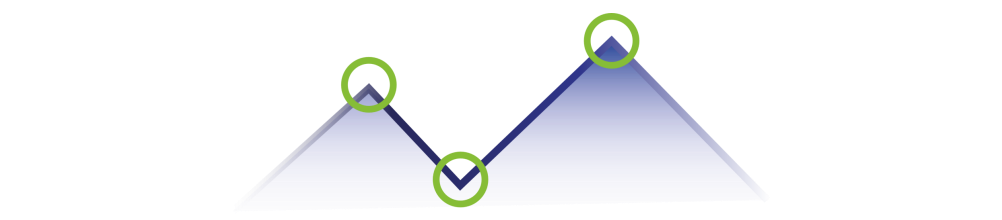일반적으로 corner는 위와 같이 뾰족하게 존재한다. 이러한 corner point는 자세히 살펴보면 여러 선분들이 교차하는 것을 확인할 수 있다.

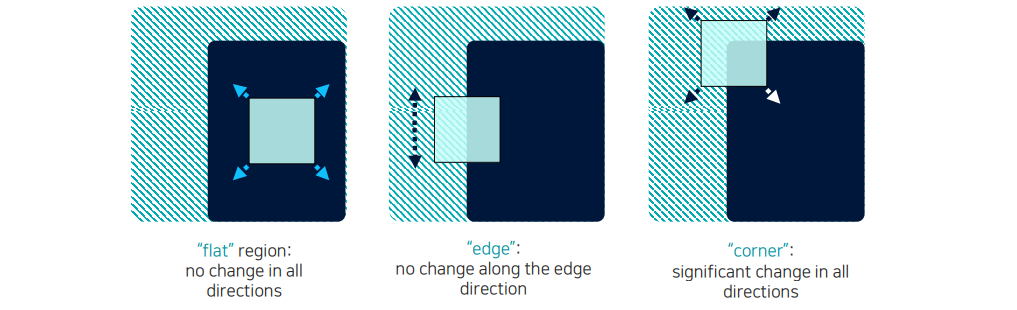Corner를 찾기 위해서 작은 window를 만들고, 이를 이동시키면서 내부를 살펴보려고 한다. 내부의 정보가 어떻게 변하는지 살펴보면 corner인지 아닌지 알 수가 있다. 만약 flat region이라고 한다면 window를 이동시키더라도 내부에서 어떠한 정보도 변하지 않을 것이다. 여기서 edge region이 된다면 만약 window를 edge 방향으로 sliding한다면 이 또한 내부에서는 변화가 없을 것이다. 이 경우에 수직한 방향으로 움직인다면 값의 차이가 많이 발생하게 될 것이다. 하지만 만약 이러한 작은 window가 corner point 위에 존재한다면 어떠한 방향으로 움직이더라도 내부의 정보가 많이 변할 것이다. 즉, 우리는 window를 shifting하면서 intensity가 얼마나 크게 변하는지 확인하면 corner를 찾을 수 있을 것이다.

이러한 corner를 찾는 알고리즘인 Harris corner detector는 한마디로 image gradient를 이용해서 corner를 찾는다고 이야기할 수 있다. Image gradient는 영상에서 object의 경계선을 추출할 때 구해서 사용했었다. 그래서 image gradient를 이용해서 위와 같은 순서로 corner를 찾게 될 것이다. 가장 먼저 $x$축의 gradient와 $y$축의 gradient를 구해서 우선은 작은 영역에 대해서 살펴볼 것이다. 그 다음에는 image gradient로부터 평균을 제거하고 gradient 정보들의 covariance matrix를 구하게 될 것이다. 그리고는 covariance matrix의 eigenvalue와 eigenvector를 분석해서 flat, edge, corner region인지 판단할 것이다. 마지막에는 간단한 rule을 사용해서 threshold를 통해서 eigenvalue를 비교하여 corner임을 판단할 것이다.

1. Compute image gradients over a small region

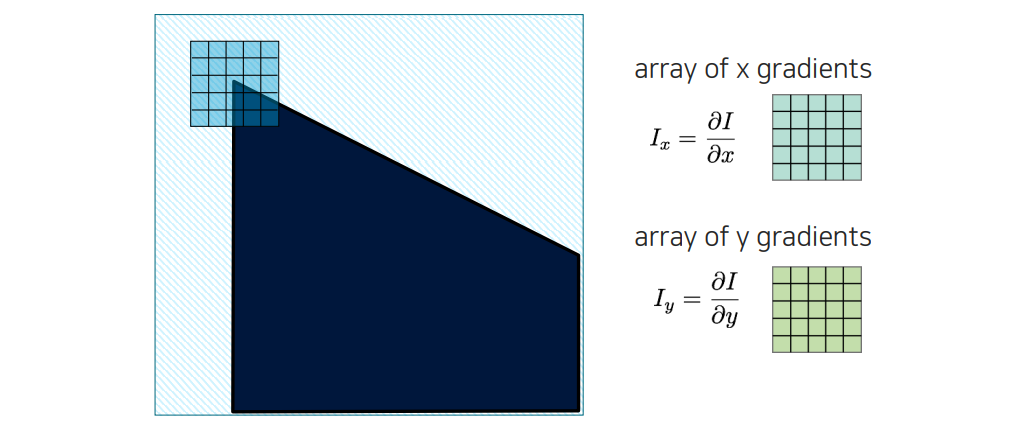Image gradient를 작은 영역에서 구한다고 하면 위와 같이 작은 window를 두고 양 축을 기준으로 미분을 취해서 gradient 값들을 얻게 될 것이다.

영상이 어떻게 생겼는지에 따라 각각의 gradient는 위와 같이 형성될 것이다. 경계선에서는 큰 값이 나오게 되며 경계선이 아닌 곳에서는 낮은 값들이 추출될 것이다. 우리는 이러한 미분 결과를 통해서 corner인지 아닌지 확인해볼 것이다.

각각의 region에서 gradient를 구하게 되면 위와 같이 분포하게 될 것이다. 각 pixel마다 gradient의 값의 크기를 비교한 것이다. 위 예시에서 edge 성분의 경우에는 $x$축에 미분을 취했을 때 값의 편차가 크게 날 것이다. Corner point 부분에서 2차원에 그려보면 양쪽 축 모두 큰 편차를 보일 것이다. 이러한 분포를 보았을 때 해당 영역이 어떠한 형태를 취하는지 생각해볼 수 있게 된다. 이러한 형태들을 구분함으로써 corner detector를 만들 수 있는 것이다. 그렇다면 여기서 어떻게 orientation과 magnitude를 판별해서 해당 영역이 어떠한 분포를 보이는지 찾을 수 있을까?

2. Subtract the mean from each image gradient

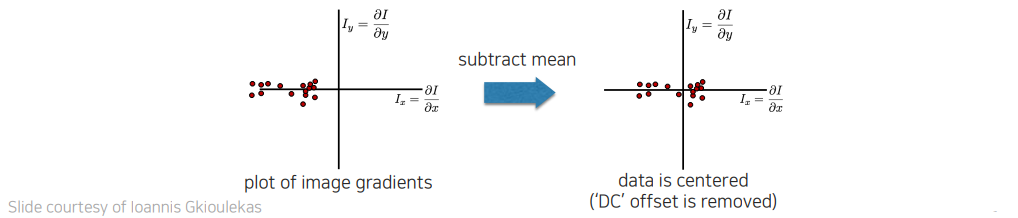
방향과 크기를 판별하기 위해서는 먼저 image gradient를 중심에 두고 분석해야 한다.
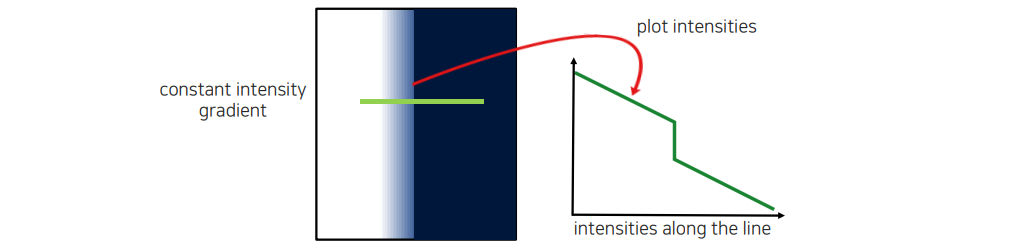
Edge 근방에서 gradient가 꾸준히 발생하는 경우에서 intensity를 plot해서 보게 되면 값이 크게 변하는 지점이 있을 것이다. 이러한 경우에는 image gradient 값들이 한쪽에 쏠려있게 된다. 여기서 normalization을 통해서 어느 방향으로 퍼져있는지만 보고서 판단을 할 수 있다. 이때 얼마나 멀리 퍼져있는지는 여기서는 크게 중요하지 않을 것이다.

3. Compute the covariance matrix

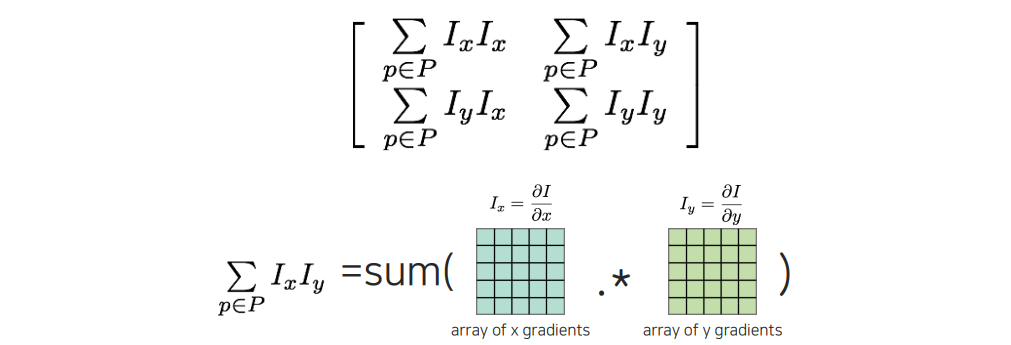이러한 상황에서 covariance matrix를 구해줘야 한다. Covariance matrix는 평균 값을 빼줬기 때문에 위와 같이 평균이 0인 상태로 만들어지게 될 것이다. 결국 구현은 각 image patch로부터 element-wise multiplication을 해주고 summation을 취하게 되는데, 이는 곧 patch 사이의 내적을 의미하게 된다. 그렇다면 왜 이렇게 covariance matrix를 계산을 해야하는지 생각해 본다고 한다면 어디서부터 covariance matrix가 왔는지 생각해보면 된다.

이전에 corner point는 조금만 움직여도 window 안의 intensity 값들이 변하는 것을 확인할 수 있었다. 그래서 intensity가 얼마나 변하는지에 대한 function을 먼저 제안을 하고 이를 분석함으로써 어떠한 식으로 corner를 찾을 수 있는지 유도할 수 있다.

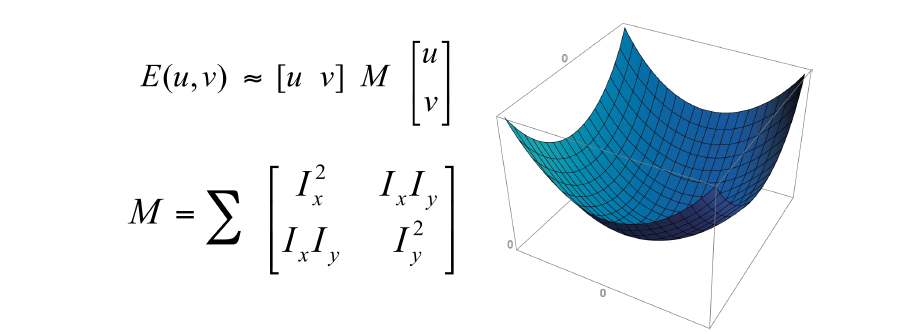
이러한 함수는 위와 같이 정의가 된다. Error function을 정의하게 되는데, 조금만 움직였을 때 얼마나 intensity 차이가 있는지 측정하는 것이다.$u,v$만큼 움직이는 상황에서 원래 위치에 비해서 얼만큼의 intensity가 변했는지 측정하는 것이다. 추가적으로 영상의 중심부가 중요하다는 가중치를 두기 위해서 window function을 사용하기도 한다. Intensity 차이의 합에 대한 error를 이렇게 구할 수가 있고, 이 값이 커지게 되면 해당 지점이 중요한 corner point임을 알 수가 있는 것이다.

Error function approximation

우리는 $u,v$가 가장 큰 변화를 가지는 point를 소수 단위로 정교하게 구하기 위해서 first-order Taylor expansion을 사용할 것이다. 그리하여 현재 위치에서 Taylor approximation을 사용해서 $u,v$가 어떻게 되었을 때 가장 민감하게 반응하는지 측정하고자 한다. 여기서 우리는 notation을 살짝 수정하여 $\vec{x}={x\choose y}$라 하고 $\Delta={u\choose v}$로 표기하고자 한다. 이제 $\Delta$ 부분이 유일한 input이기 때문에 이에 대해서 Taylor approximation을 하면 현재 위치를 $\vec{x}$라고 두었을 때, $I(x+u,y+v)$는 $I(\vec{x})+\vec{\Delta}^TI'(\vec{x})$가 될 것이다. 그랬을 때 $\vec{\Delta}^TI'(\vec{x})$ 부분은 $\begin{bmatrix}u & v\end{bmatrix}\begin{bmatrix}I_x \\ I_y\end{bmatrix}$가 될 것이다. 우리는 앞서 $I(\vec{x})$ 부분은 뒤의 $I(x,y)$ 부분과 지워지게 되어 결국 우리는 $\begin{bmatrix}u & v\end{bmatrix}\begin{bmatrix}I_x \\ I_y\end{bmatrix}$를 제곱하는 형태만 남게 될 것이다. 제곱을 해주게 되면 $\begin{bmatrix}u & v\end{bmatrix}\begin{bmatrix}I_x \\ I_y\end{bmatrix}\begin{bmatrix}I_x & I_y\end{bmatrix}\begin{bmatrix}u \\ v\end{bmatrix}$가 될 것이고, 여기서 $\begin{bmatrix}I_x \\ I_y\end{bmatrix}\begin{bmatrix}I_x & I_y\end{bmatrix}$는 결국 $\begin{bmatrix}I_xI_x & I_xI_y \\ I_yI_x & I_yI_y\end{bmatrix}$가 될 것이다. 최종적으로 우리는 $\sum_{x,y} w(x,y)\vec{\Delta}^T\begin{bmatrix}I_xI_x & I_xI_y \\ I_yI_x & I_yI_y\end{bmatrix}\vec{\Delta}$가 된다. 여기서 $\sum_{x,y}w(x,y)$ 부분이 linear하기 때문에 안쪽으로 들어가면 우리는 weighted covariance matrix를 얻게되는 것이다.

Bilinear approximation

이러한 식으로 가운데 $2\times2$ matrix가 유도가 되게 되고, energy function은 first-order Taylor approximation에 의해서 $x_0$ 근처에서는 위와 같이 간단하게 quadratic form으로 정의가 되게 된다. 위에서 구한 $M$은 second moment matrix라고도 부르며 structure tensor라고도 부른다.

우리는 지금까지 covariance matrix를 구했는데, 이러한 covariance matrix하고 energy function은 2차 함수의 관계를 가지고 있다. 그렇다면 이제 이 2차 함수에서 가장 민감한 부분을 어떻게 찾을지 생각해봐야 한다.

Error function을 우측과 같이 그려볼 수 있다. $u,v$는 각각 $x,y$ 축을 의미하게 되고, $z$ 축을 error function의 값으로 생각할 수 있다. 좌측의 수식은 결국 우측과 같이 표현되게 되고, 전체 error에 대한 surface를 quadratic form으로 approximation 했다고 할 수 있고, $M$이 정보를 포함하고 있다고 생각하면 된다. 이때, 가장 민감하게 변하는 부분은 꼭지점 부분일 것이기에 이러한 point들을 찾는 문제가 될 것이다.

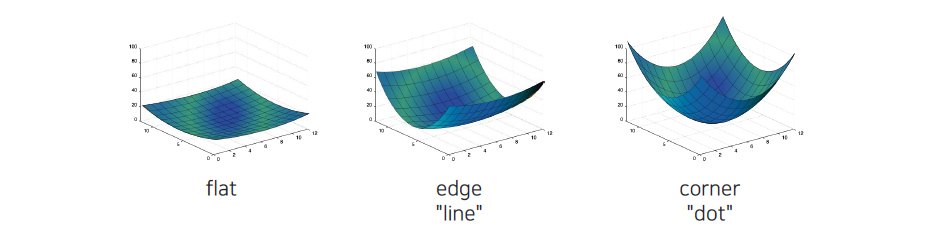Error surface가 어떠한 특성을 가지고 있는지 살펴보면, 가장 먼저 어디를 가더라도 error가 커지지 않는 것이 바로 flat region을 의미하게 된다. 특정 방향으로 갔을 때 error가 급격히 커지면 이는 edge가 될 것이고, 어느 방향으로 가더라도 error가 커지면 이는 corner가 될 것이다.

4. Compute eigenvalues and eigenvectors

이번에는 paraboloid 형태로 quadratic form으로 표현한 error function에 대해서 꼭지점을 어떻게 찾는지에 대해서 알아보고자 한다. Covariance matrix가 어떠한 식으로 움직일 때 eigenvalue하고 eigenvector가 어떻게 변하게 되고, intensity가 어떠한 방향으로 갔을 때 빠르게 변하는지, 그리고 어떠한 위치에서 그 변화가 가장 최대화가 되는지 찾는 방법에 대해서 알아보려고 하는 것이다.

먼저 Harrix corner의 error function은 quadratic form으로 정의할 수 있고 Taylor expansion을 이용해서 approximation 할 수 있었다.

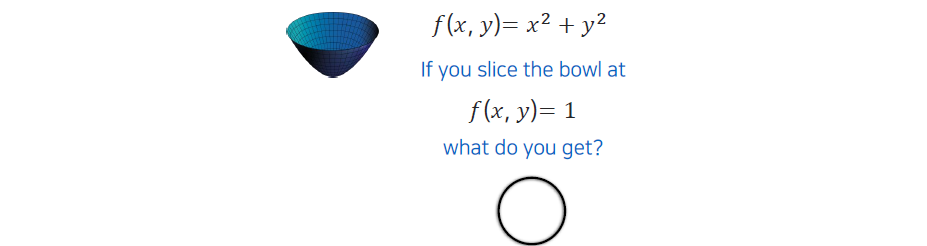
우리는 paraboloid를 분석하기 위해서 간단하게 단면을 보려고 한다. 일반적으로 $f(x,y)$를 표현해놓고 특정 위치에 대해서 단면을 찾아서 볼 수가 있다.
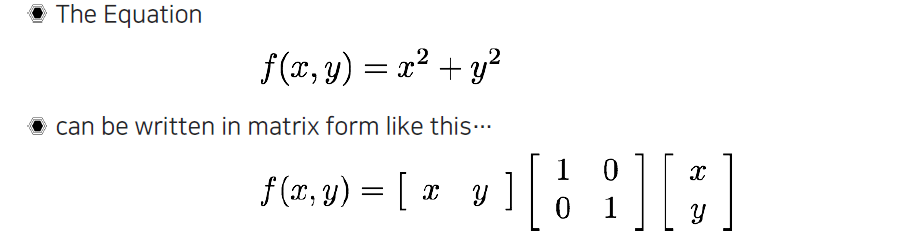이제 수식을 나타낼 때 matrix 형태로 표현하게 되면 조금 더 equation의 의미와 직관성을 얻을 수가 있다. 이때 형태를 보면 지금까지 보았던 first-order Taylor approximation을 사용해서 만든 2차항과 매우 닮은 것을 볼 수 있다. 그래서 우리는 이를 통해서 어떠한 식으로 움직이는지와 가운데 $M$ matrix가 무엇을 의미하는지 살펴보고자 한다.

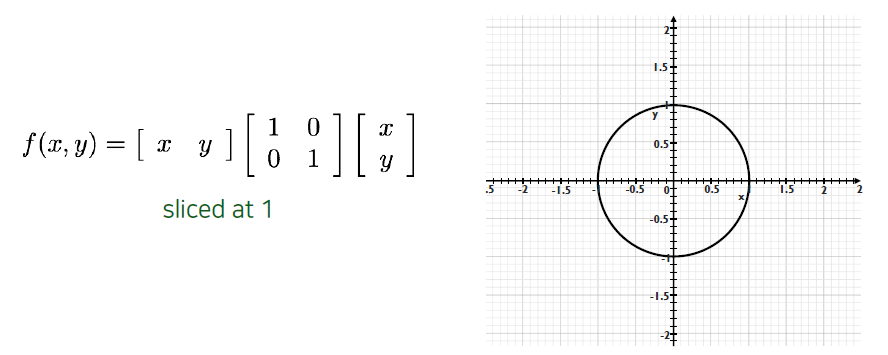$M$이 identity matrix일 때 $f$가 1을 만족하는 등고선을 그려보면 우측과 같다.

만약 $x$에 해당하는 coefficient의 값을 바꿔주게 되면 우측과 같이 $x$의 폭이 줄어든 것을 볼 수 있다. 이는 paraboloid 관점에서 $x$가 커짐에 따라서 error 값이 커지는 속도가 2배만큼 빨라진 것이다. 그래서 같은 $f$가 1인 등고선을 그렸을 때 속도가 빨라졌기 때문에 폭이 줄어들게 된 것이다.

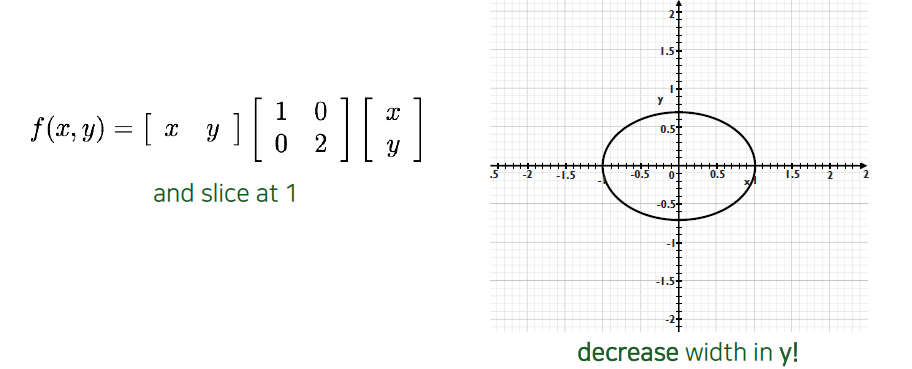반대로 $y$에 대한 coefficient를 키워주게 되면 $y$ 축 폭이 줄어들게 된다. 결국 우리는 가운데 $M$ matrix를 통해서 shape을 파악할 수 있다는 것을 알게 되었다. 그렇다면 이제 $M$ matrix와 eigenvalue, eigenvector 사이의 관계에 대해서 살펴볼 수가 있다.

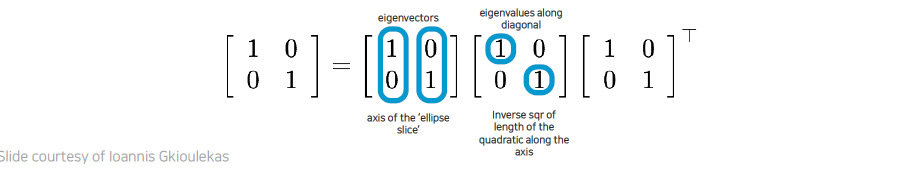우리가 SVD를 하게되면 eigenvalue와 eigenvector를 얻을 수 있게 된다. Eigenvalue가 의미하는 바는 eigenvector의 scale을 의미하게 된다.

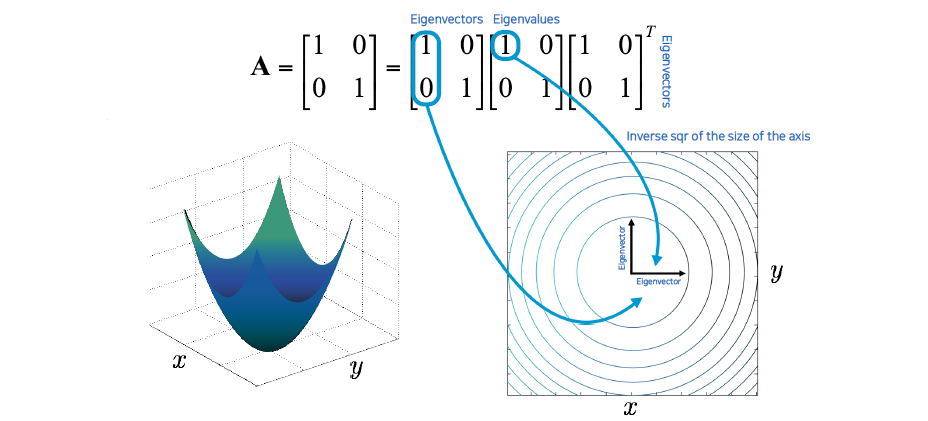그래서 identity matrix를 eigen decomposition을 통해서 분리를 했을 때, eigenvector는 축을 나타나게 되고 eigenvalue는 축의 길이를 나타내게 되는 것이다.

$x$의 coefficient를 키우게 되면 $x$ 축의 폭이 줄어든 것을 확인할 수가 있고, eigenvector의 길이는 그만큼 길어지는 것을 볼 수 있다. 지금까지는 간단한 eigenvector들만을 고려해보았다.

만약 eigenvector가 간단하게 구성되어 있지 않다면 조금 더 고민해 볼 필요가 있다. 이러한 경우에는 해당 eigenvector만큼 축의 방향이 돌아갔다고 생각하면 된다. 그리고 해당 축에서 eigenvalue만큼 변했다고 볼 수 있다.

지금까지 $M$ matrix가 general하게 주어졌을 때 어떠한 식으로 분석을 할 수가 있는지 paraboloid function이 어떻게 움직이고 shape이 어떻게 되는지 살펴보았다. 이를 좀 더 수학적으로 엄밀하게 따져보기 위해서 eigenvector와 eigenvalue를 구하는 eigen decomposition을 자세하게 살펴보고자 한다.

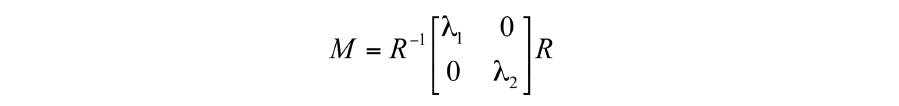일반적으로 $M$이 symmetric하면 위와 같이 분리가 된다. $R$ 자체가 orthonormal matrix이기 때문에 transpose와 inverse가 동일하게 된다.

$M$ matrix의 $\lambda$ 값에 따라서 장축과 단축의 길이가 형성이 되게 되고, shape이 만들어지게 되는 것이다. $M$의 $\lambda$ 값 자체가 분포의 장축과 단축 정보를 의미하고 있다는 것을 알 수가 있다. 이를 이용해서 gradient plot에서 원점에 모이는지, 아니면 여기저기 흩어져 있는지 또는 한쪽으로만 번져 있는지를 $\lambda$를 통해서 확인할 수 있다.

Interpreting eigenvalues

위와 같이 $\lambda$ plot을 그렸을 때 크게 4개의 영역으로 나눠서 생각할 수 있다. 각 image patch가 주어지고 이를 분석했을 때 어느 영역에 존재하는지에 따라서 corner인지 아닌지를 판단할 수가 있다.

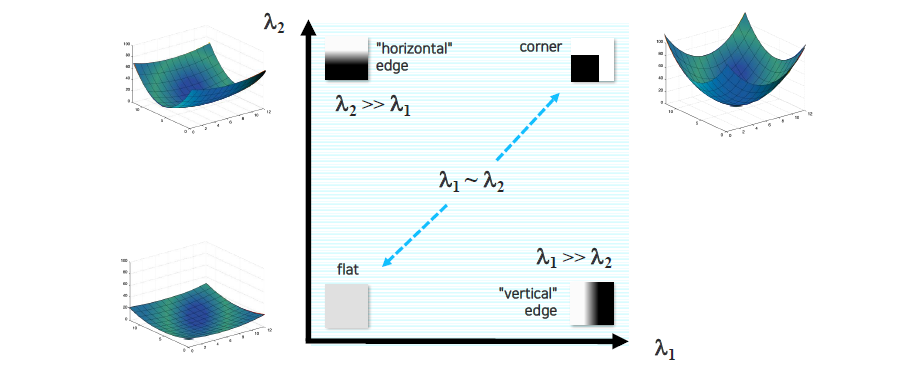한쪽 $\lambda$ 값이 더 큰 경우에는 한쪽으로의 변화가 굉장히 크다는 것을 의미하고 이는 곧 edge를 나타낼 것이다. 만약 서로 비슷한데 둘다 작은 경우에는 flat region을 의미하고 둘다 큰 경우에는 corner region을 의미할 것이다.

5. Use threshold on eigenvalues to detect corners

이번에는 thresholding을 이용하여 간단한 eigenvalue 기반의 corner를 탐지하는 기법에 대해서 알아보고자 한다. Threshold 하나로 어떻게 corner를 탐지할 수 있는 것일까? 요약하자면 corner를 찾기 위하여 eigenvalue 기반의 판별식을 세운다고 볼 수 있을 것이다.

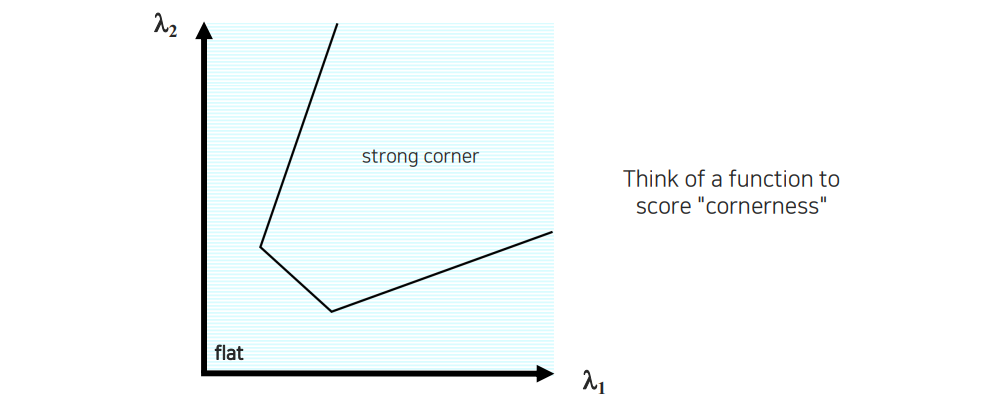2차원에 eigenvalue 2개를 놓고서 corner인지 아닌지 판단할 것이다. 위에서 보았듯이 좌측 상단과 우측 하단은 edge의 영역이고 좌측 하단은 flat의 영역이었다. 나머지 부분만이 corner를 가리키는 영역이 된다.

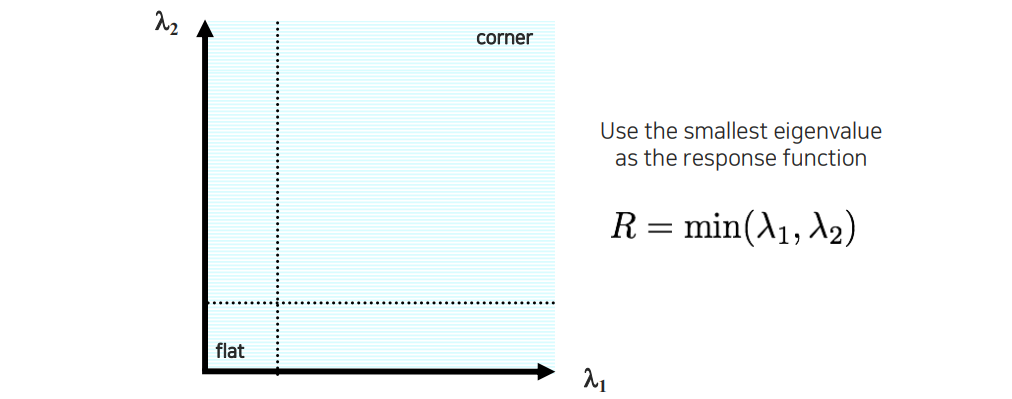Eigenvalue 2개 중에서 작은 값이 하나라도 있다면 그 값이 특정 threshold $T$ 보다 큰 경우에 대해서 우리는 corner라고 판단하고자 한다.

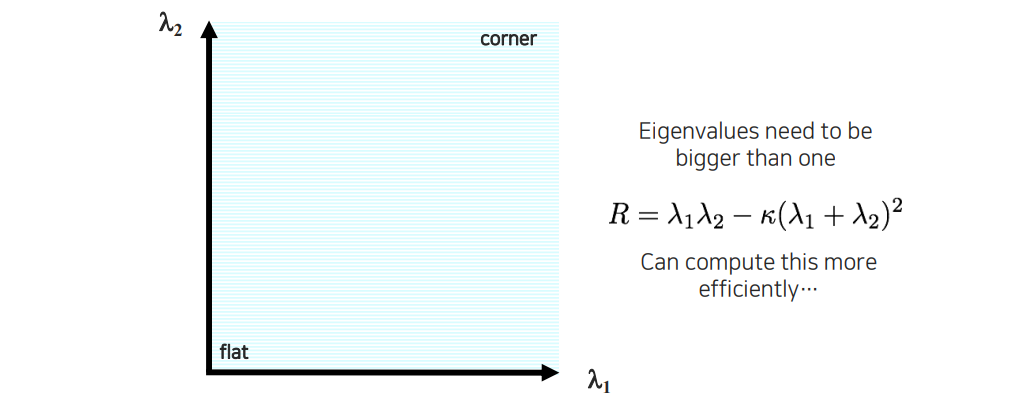또 다른 방법으로는 위와 같이 수식을 세워서 판단할 수도 있다. Response $R$을 위와 같이 계산하고 그 값을 이용하여 corner를 판별하는 것이다. 이것의 기준 조건은 어떠한 값보다 eigenvalue가 크면 좋겠다는 것이다. 단순히 작은 eigenvalue가 특정 조건보다 큰 것이 아니라 eigenvalue들이 적어도 1보다는 큰 값을 가져야 한다는 것이다.

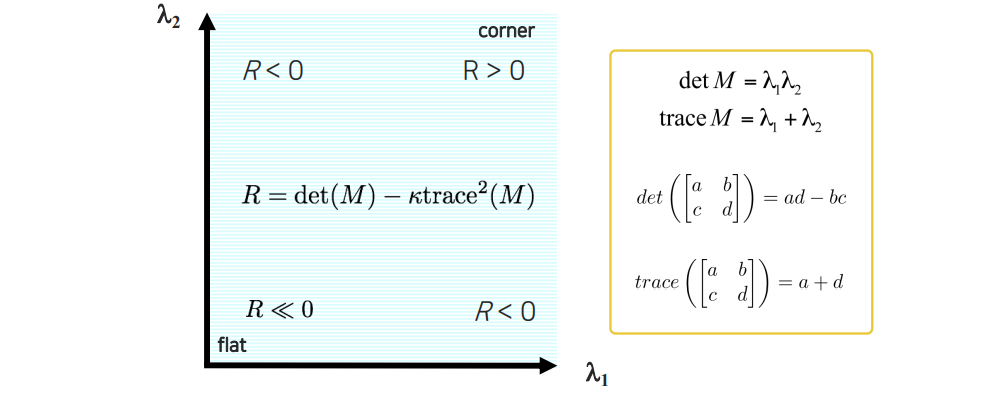앞의 항은 determinant로 eigenvalue가 모두 큰 경우에만 해당 항이 커지게 된다. Corner region을 잘라내는 판별식을 직접 디자인했다고 볼 수 있다.

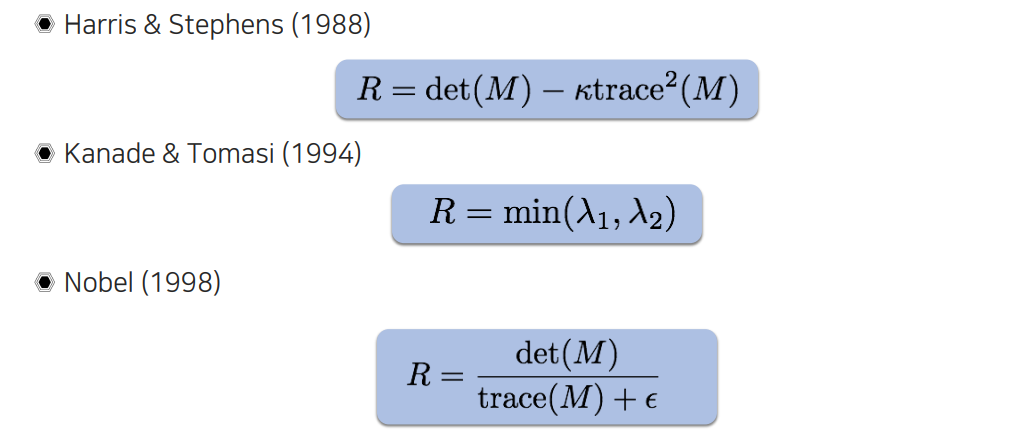Corner를 판별하는 식들의 경우 옛날 알고리즘들은 사람이 직접 위와 같이 디자인해서 사용했다. Determinant와 trace를 이용하여 특정 값보다 크다든지, 아니면 단순히 min을 취하든지해서 eigenvalue로부터 corner를 찾았었다.

Harris corner response is invariant to rotation

Corner point의 중요한 특성 중 하나가 바로 rotation invaraince이다. 어떠한 rotation을 했을 때 eigenvalue의 shape은 항상 같게 유지가 된다. Eigen decomposition을 하게 되면 $M$ matrix 가운데는 diagonal matrix가 생기게 되고 앞뒤로 orthonormal matrix가 곱해지게 된다. 앞뒤로 곱해진 matrix는 rotation matrix의 역할을 하고 $M$ matrix의 경우에는 diagonalization 역할을 하게 된다. 그래서 어떠한 식의 corner든지 eigen decomposition을 하게 되면 장축과 단축을 기준으로 diagonal component들이 결정이 되기 때문에 2개가 만약 동일한 corner 특성을 가지고 있다고 한다면 rotation에 상관없는 response가 나오게 된다. 그렇기 때문에 corner response는 rotation에 굉장히 강인한 편이고, 이는 굉장히 좋은 성질이 될 수 있다.

Harris corner response is invariant to intensity changes

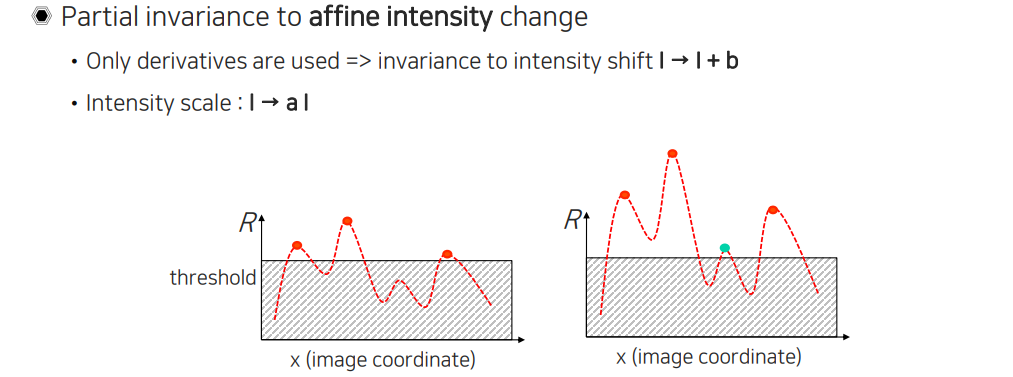Haris corner response는 또한 intensity change에 invariant하다는 좋은 특성이 있다. 여기서 intensity change는 affine 관계에서 invariance를 가지게 되고, 이는 partial invariance라고 한다. 우선 affine이라고 하면 더해주는 offset과 곱해주는 scale이 모두 있는 것을 의미한다. Offset에 invariance가 생기는 이유는 Harris corner를 구할 때 미분 값을 사용하게 되는데 그랬을 때 intensity image에 미분을 취하게 되면 offset 부분이 사라져 원래의 미분 값이 그대로 남기 때문이다. 그래서 전체적인 offset을 통해서 영상을 밝게 만드는 것과 어둡게 만드는 것과는 상관없이 Harris corner를 찾는 것과는 상관이 없게 된다. Intensity scale에 대한 invariance는 미분을 하더라도 앞에 상수가 곱해지기 때문에 미분값이 커질 수가 있다. 그래서 우측처럼 threshold 값을 넘는 값이 생길 수가 있다. 앞에 곱해지는 값에 따라 threshold를 넘을 수도 있고 아닐 수도 있기 때문에 이를 partial invariance라고 하는 것이다. Offset도 이에 대해서는 마찬가지이다. 원래 intensity가 10인에 20을 빼주게 되면 음수를 가지기 때문에 다 0으로 될 것이다. 결국 부분적으로 invariant 하기 때문에 partial invariance가 되는 것이다.

Harris corner response is not invarint to scale

앞서 rotation이나 intensity change에 Harris corner가 invariance를 가진다고 했는데, 이번에는 그렇지 않은 경우에 대해서 알아보려고 한다. Harris corner는 scale에 invarint하지 않는다. 우리가 부분적으로 보았을 때 edge라고 보이는 부분이 scale을 바꿔서 보았을 때 corner로 보일 수가 있을 것이다. 그래서 scale에 따라서 edge로도 보일 수 있고, corner로도 보일 수 있기 때문에 Harris corner는 scale에 variance를 가지고 있다고 할 수 있다.

Multi-scale blob detection

그래서 Harris corner가 multi scale에 취약한데 이를 보완하기 위해서 multi-scale blob detection이라는 것이 제안되기도 했다.

Multi-scale detection

우선 multi-scale detection이 무엇인지 알아볼 것이다. 단순하게 생각하면 scale을 여러개를 사용해서 detection을 하겠다는 것이다. 여기서 궁극적인 목적은 이러한 corner detector나 feature detector들을 scale이 바뀌더라도 동일한 point가 찾아질 수 있도록 scale invariant하게 만드는 것이다. 여기서 scale을 여러개 사용한다는 것은 모든 scale을 사용한다는 것이 아니고 scale 중에서 적절한 corner point가 어딘지를 찾아주는 것들을 사용하겠다는 것이다.

위와 같이 해바라기가 여러개 있다고 했을 때 가까이 있는 해바라기는 원의 형태로 잘 표현이 되고 크기가 큰 반면 멀리 있는 해바라기는 상대적으로 크기가 작은 것을 볼 수 있다. 1장의 image 내에서도 scale의 차이가 존재하는 것을 볼 수 있다. 그래서 scale에 굉장히 민감한 알고리즘들이 어떻게 영상에 적용이 되는지 고민이 많았었고, 이때 사용하는 것이 multi-scale detection이다.

Multi-scale blob detection

Multi-scale blob detection이라는 것은 corner point가 민감하게 변하게 되는데 이때 position과 scale을 같이 찾아야하는 문제가 된다. 그래서 local하게 어디가 maximum point인지 position $x,y$와 scale $\sigma$까지 3개의 parameter를 찾는 문제가 된다. 위의 예제를 보면 2개의 예시가 있고 region size가 커짐에 따라 blob detection의 response가 변하는 추이를 나타내고 있다. Image 1의 경우 작은 부분을 보면 edge처럼 보이지만 범위를 넓힘에 따라 점점 corner로 보이게 된다. 그래서 window size를 키우다보면 어느순간 cornerness가 크게 보이는 지점이 생기고 이때 response 값이 가장 크게 나타날 것이다. 그래서 떨어지게 되는 순간에 가장 높은 곳이 local maximum point가 되는 것을 알 수 있다. Image 2의 경우에는 window size를 키우게 되었을 때 어느순간 여러개의 corner가 보이게 될 것이다. 이 경우 window size를 크게해서 보면 어느 순간 선처럼 보일 수도 있을 것이다. 그래서 너무 키우면 response가 많이 떨어지게 될 것이다. Window size를 적절하게 만들어 local maximum point를 찾는 것이 중요하다.

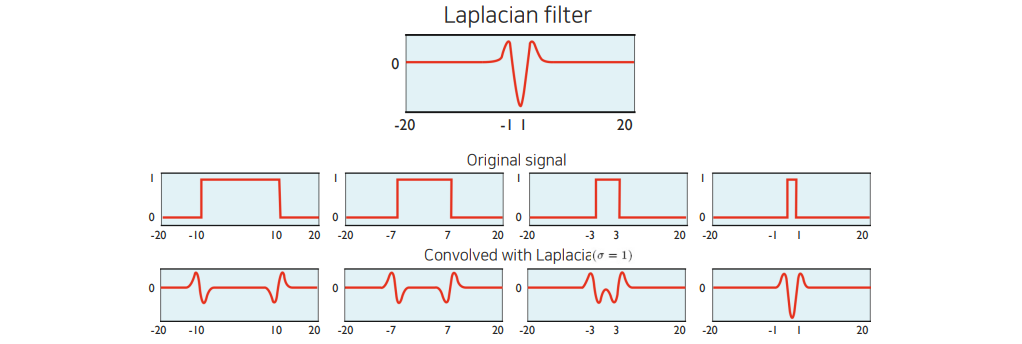Multi-scale blob detection을 할 때 우리가 blob detection을 위한 filter가 필수적으로 필요하다. 이번 예시를 통해서 간단하게 Laplacian filter를 사용해서 multi-scale blob detetction을 어떻게 하는지 보고자 한다. Filter를 기반으로 response를 보게 되는데, 여기서 response가 가장 큰 값을 가지는 형태를 찾아야 한다. Original signal에 따라 Laplacian filter가 적용된 부분에서 그 폭이 줄어들고 있는 것을 볼 수 있다. 만약 signal의 폭과 Laplacian filter의 폭이 거의 일치하게 되면 response가 크게 peak를 보이게 된다. 결국 우리는 이렇게 절대값이 큰 response를 찾는 것이 목적이며, 이는 곧 multi-scale의 blob detection을 하는 것과 마찬가지가 된다. Scale은 Laplacian filter의 폭으로 조절하면 된다.

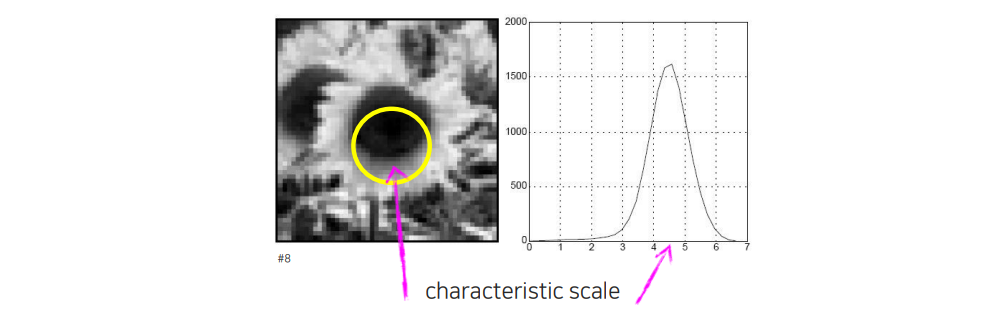그래서 charateristic scale은 filter response가 peak를 치는 부분을 말한다. Charateristic scale은 물체의 특성을 반영하게 된다. Filter response가 peak 치는 부분은 우리가 filter 디자인을 어떻게 하느냐에 따라서 달라지게 된다. 우리가 characteristic scale을 찾기 위해서는 결국엔 scale space에서 여러개를 test해보고 찾는 방법 밖에 존재하지 않는다.

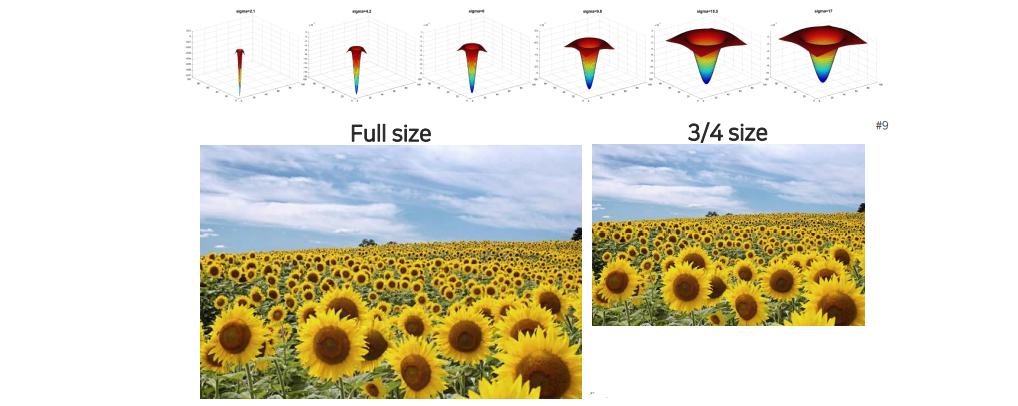Laplacian filter를 크기별로 정해놓고 full size의 image에 적용시켜 response를 보거나 image의 size를 줄여서 적용해보는 방법도 존재할 것이다.

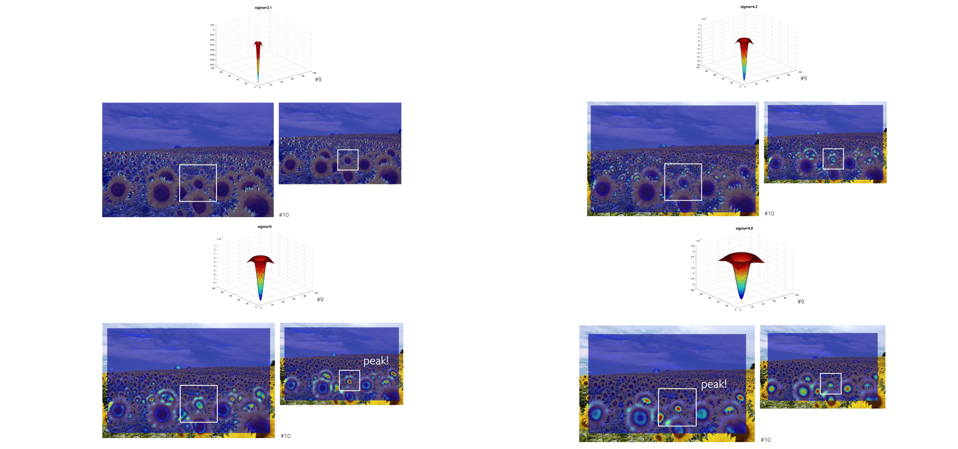Filter의 크기를 바꿔가면서 적용해보면 image의 크기에 따라 response가 peak를 치는 filter가 생기게 될 것이다. 이러한 과정으로 blob을 찾을 수 있고 가운데에 있는 물체의 shape의 크기나 형태에 따라 이에 맞는 Laplacian filter가 존재하게 되고 이를 모두 test를 함으로써 response가 peak 되는 지점을 찾을 수 있는 것이다.

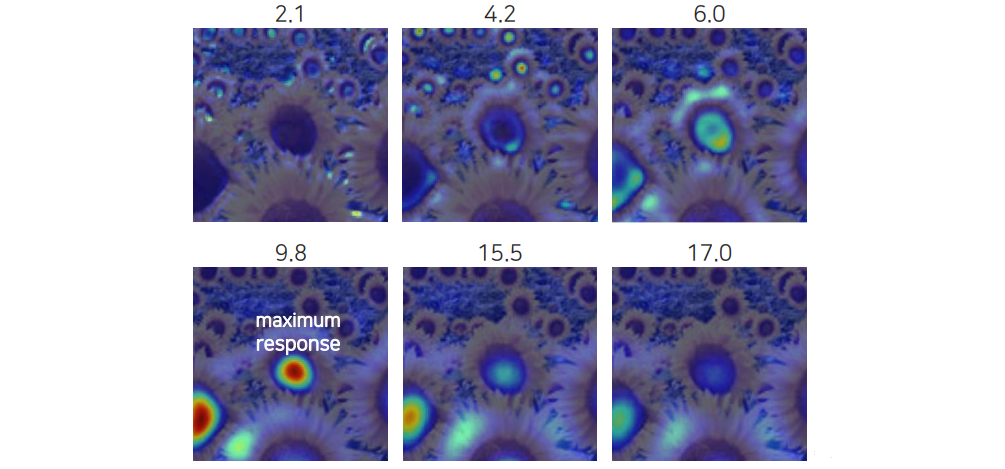Blob detection 말고도 다른 multi-scale 알고리즘들도 이러한 식으로 maximum response를 scale space에서 찾을 수 있다.

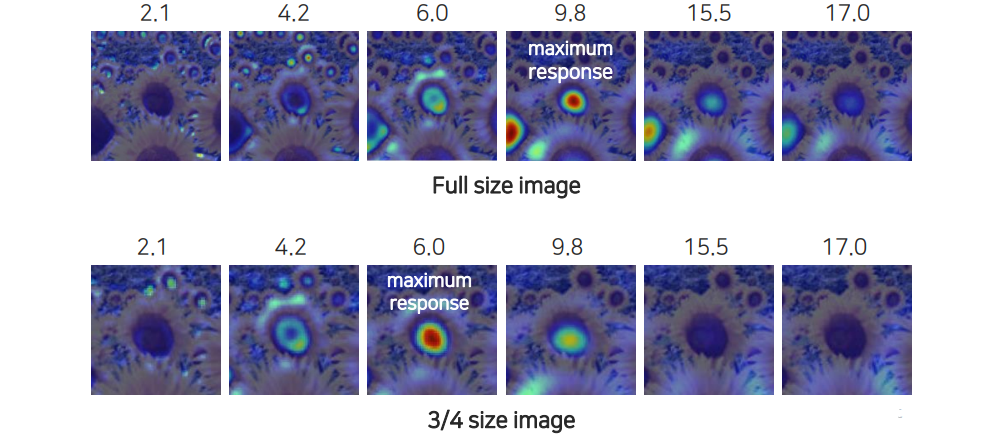Full size image하고 size를 줄인 image를 보면 원래 object의 크기가 영상을 줄이게 되면 같이 작아지게 된다. 그래서 maximum response가 발생하는 지점이 영상의 크기에 따라 달라지게 되고, 이에 따라 optimal scale을 찾을 수가 있다.

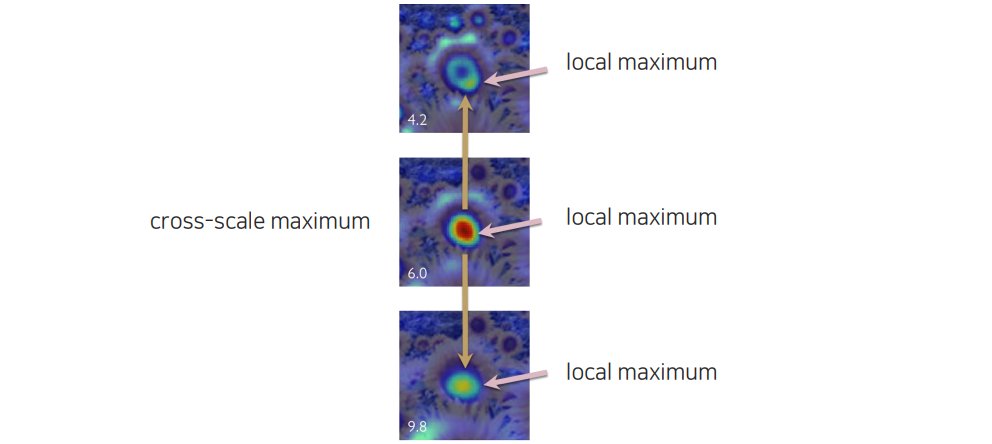Cross-scale maximum이라고 해서 scale 사이에서 비교를 하면서 어느 지점이 local maximum point인지를 알 수가 있는데, 한 영역에서만 보는 것이 아니라 scale 축에서도 봐야 한다. 그래서 공간 축에 local maximum을 찾는 것 뿐만 아니라 scale 축에서도 함께 찾아야 한다.

그렇다면 이러한 scale을 어떻게 선택을 할 수 있을까? 예시로 Laplacian filter를 보았지만 Harris corner detector도 multi-scale로 사용할 수가 있는 것이다. 그리고 Laplacian filter를 만들 때 Gaussian pyramid를 이용할 수도 있다. Gaussian pyramid를 활용하고 DoG를 이용하여 조금 더 Laplacian filter를 구현할 수 있다. Scale selection 할 때 Gaussian pyramid를 활용하는 경우에는 Gaussian pyramid마다 우리가 local maximum이고 cross-scale에서 maximum인 경우에는 해당 위치에서 저장을 하는 것으로 multi-scale blob detection을 수행하게 된다.