
Cut-and-Paste
Cut-and-paste는 간단한 image blending 기법 중 하나로, 2-step으로 진행이 된다.
 첫번째는 image로부터 sprite를 추출한다. Sprite는 input image와 mask가 있을 때, input image로부터 mask 모양대로 추출한 2d bitmap image이다. 그래서 추출한 모양을 제외하고는 투명한 pixel을 가지게 된다.
첫번째는 image로부터 sprite를 추출한다. Sprite는 input image와 mask가 있을 때, input image로부터 mask 모양대로 추출한 2d bitmap image이다. 그래서 추출한 모양을 제외하고는 투명한 pixel을 가지게 된다.
 두번째 step은 bleding하기를 원하는 image들로부터 sprite를 합쳐서 위와 같은 결과를 얻는 것이다. Cut-and-paste는 collaging이라고도 불린다.
두번째 step은 bleding하기를 원하는 image들로부터 sprite를 합쳐서 위와 같은 결과를 얻는 것이다. Cut-and-paste는 collaging이라고도 불린다.
 때때로 cut-and-paste는 시각적으로 매력적인 결과를 만들기도 한다.
때때로 cut-and-paste는 시각적으로 매력적인 결과를 만들기도 한다.
 그러나 가끔 의도치않게 결과가 만들어지기도 한다. 펭귄을 자연스럽게 합치고 싶었지만, 부자연스럽게 합쳐져버렸다. 도대체 무엇이 문제일까?
그러나 가끔 의도치않게 결과가 만들어지기도 한다. 펭귄을 자연스럽게 합치고 싶었지만, 부자연스럽게 합쳐져버렸다. 도대체 무엇이 문제일까?
Alpha (Linear) Blending
앞서 보았듯이 cut-and-paste는 한계점이 존재하는 기법이다. 더 나은 결과를 만들기 위해서 더 정교한 blending 기법을 사용 할 필요가 있다. Alpha blending은 alpha matte 혹은 alpha composite이라고도 한다.
 Alpha blending에서는 foreground image와 background image가 필요하다. 그리고 어떻게 foreground image를 background image에 blending 해야하는지 가리키는 mask가 필요하다. Mask를 사용하면 위의 식을 사용해서 output image를 계산할 수 있다. Mask에서 하얀색이 1을 가리키게 되고 이를 foreground로부터 pixel을 이용해서 계산하고, 검은 부분은 0을 가리키는데 이를 이용해서 background image로부터 pixel을 이용해서 계산하면 된다.
Alpha blending에서는 foreground image와 background image가 필요하다. 그리고 어떻게 foreground image를 background image에 blending 해야하는지 가리키는 mask가 필요하다. Mask를 사용하면 위의 식을 사용해서 output image를 계산할 수 있다. Mask에서 하얀색이 1을 가리키게 되고 이를 foreground로부터 pixel을 이용해서 계산하고, 검은 부분은 0을 가리키는데 이를 이용해서 background image로부터 pixel을 이용해서 계산하면 된다.
Binary Alpha Mask
 Image의 일부분으로 펭귄이 composite이 된다. 경계선이 너무 뚜렷한 문제가 있어 image가 부자연스러워보인다. 이렇게 뚜렷한 경계선 대신에 smooth한 변화가 필요해보인다.
Image의 일부분으로 펭귄이 composite이 된다. 경계선이 너무 뚜렷한 문제가 있어 image가 부자연스러워보인다. 이렇게 뚜렷한 경계선 대신에 smooth한 변화가 필요해보인다.
Non-Binary Alpha Mask
 그래서 alpha mask를 smooth하게 만들도록 feathering이라는 개념이 도입되었다. Smoothed mask를 이용해서 image를 blending 할 수 있다. 그렇다면 어떻게 feathering이 동작하는 것일까? 매우 간단하게 Gaussian smoothing을 이용하면 된다. 우리는 어떠한 lowpass filter를 binary mask에 사용해서 smoothed mask를 만들 수 있다. 그러면 이 smoothed mask를 image blending에 사용하면 된다.
그래서 alpha mask를 smooth하게 만들도록 feathering이라는 개념이 도입되었다. Smoothed mask를 이용해서 image를 blending 할 수 있다. 그렇다면 어떻게 feathering이 동작하는 것일까? 매우 간단하게 Gaussian smoothing을 이용하면 된다. 우리는 어떠한 lowpass filter를 binary mask에 사용해서 smoothed mask를 만들 수 있다. 그러면 이 smoothed mask를 image blending에 사용하면 된다.
이렇게 smoothed mask가 된다면 위에서 output을 계산하는 식에서 mask에 관한 항이 0이나 1이 되지 않고 이제는 0.5와 같은 0에서 1사이의 실수 범위로 바뀌게 된다. 그래서 blending 결과를 보면 이제는 foreground image와 background image간 경계선이 smooth 해지는 것을 볼 수 있다. 그래서 output이 더 자연스러워 보이게 된다.
만약 단순하게 binary alpha mask를 사용한다면 그 결과는 cut-and-paste와 다를 것이 없다. 그래서 alpha mask에서 중요한 점은 smooth한 결과를 위해서 non-binary alpha mask를 사용한다는 점이다. 이것이 alpha blending의 주된 아이디어이다.
Another Blending Example
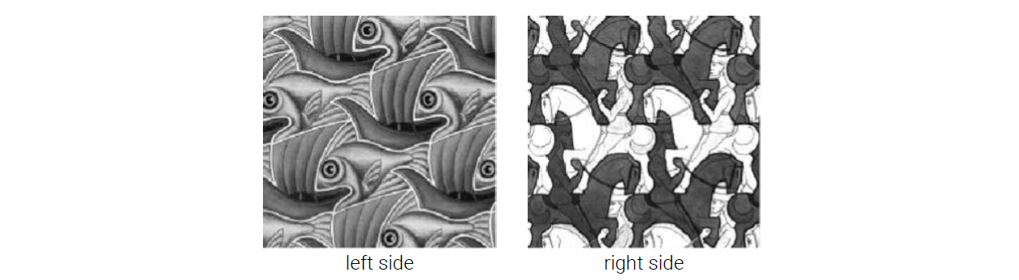 이는 또 다른 alpha bledning의 예시이고, 이 2개를 합치기 위해서 어떠한 mask를 사용해야 하는 것일까?
이는 또 다른 alpha bledning의 예시이고, 이 2개를 합치기 위해서 어떠한 mask를 사용해야 하는 것일까?
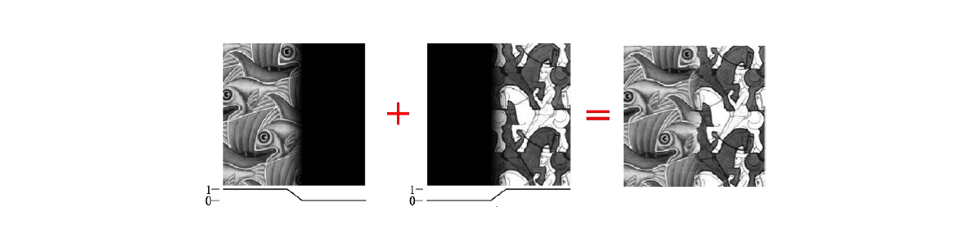 아마 이러한 구조의 mask를 사용할 수 있을 것이다. 이런식으로 하면 결과는 그리 나쁘지 않아보인다. Alpha mask를 만들 때 첫번째 image는 좌측이 1, 우측이 0인 mask를 사용 할 것이다. 그리고 중간 경계 부분인 transition area를 0과 1사이의 어떠한 값으로 해서 만들 것이다. 이 예시에서 중요한 부분은 transition area의 크기이다. 이 부분을 너무 좁게하게 되면 결과는 부자연스러울 것이다. 적당히 설정하게 되면 결과는 자연스러울 것이다. 그렇다면 어떻게 적당한 크기의 transition area를 설정해야하는 것일까?
아마 이러한 구조의 mask를 사용할 수 있을 것이다. 이런식으로 하면 결과는 그리 나쁘지 않아보인다. Alpha mask를 만들 때 첫번째 image는 좌측이 1, 우측이 0인 mask를 사용 할 것이다. 그리고 중간 경계 부분인 transition area를 0과 1사이의 어떠한 값으로 해서 만들 것이다. 이 예시에서 중요한 부분은 transition area의 크기이다. 이 부분을 너무 좁게하게 되면 결과는 부자연스러울 것이다. 적당히 설정하게 되면 결과는 자연스러울 것이다. 그렇다면 어떻게 적당한 크기의 transition area를 설정해야하는 것일까?
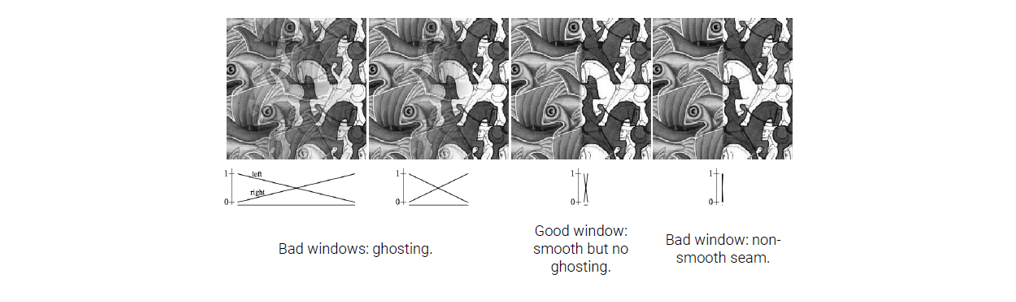 만약 transition area의 크기를 너무 크게 설정한다면, 결과는 투명한 물체가 겹쳐보이는 효과를 가져올 것이다. 이를 ghosting이라고 부른다.
만약 transition area의 크기를 너무 크게 설정한다면, 결과는 투명한 물체가 겹쳐보이는 효과를 가져올 것이다. 이를 ghosting이라고 부른다.
반대로 transition area를 너무 좁게 설정하면 경계선이 뚜렷한 cut-and-paste와 같은 결과를 만들게 된다.
Transition area를 적당히 설정하게 되면 뚜렷한 경계선이나 ghosting과 같은 현상이 일어나지 않고 자연스러운 결과를 만들어 낼 것이다.
What is a Good Window Size?
그렇다면 어떠한 크기가 transition area에 좋은 것일까?
 뚜렷한 경계선을 피하고자 한다면, window의 크기를 가장 두드러지는 feature의 크기에 맞추면 된다. 반대로 ghosting을 피하고자 한다면, window의 크기를 가장 덜 두드러지는 feature의 크기에 맞추면 된다. 사실 이러한 규칙은 서로 모순된다.
뚜렷한 경계선을 피하고자 한다면, window의 크기를 가장 두드러지는 feature의 크기에 맞추면 된다. 반대로 ghosting을 피하고자 한다면, window의 크기를 가장 덜 두드러지는 feature의 크기에 맞추면 된다. 사실 이러한 규칙은 서로 모순된다.
만약 다른 크기의 특징이 여러군데 나타난다면 적절한 크기를 설정하는 것이 다소 어려울 수 있다. 이것이 alpha blending의 문제점이다. 이러한 문제는 어떻게 해결해야할까?
Multi-Band Blending
위의 문제를 해결하고자 multi-band blending이 등장하였다.
Time to Use Pyramdis Agian
Multi-band blending의 주된 아이디어는 다음과 같다.
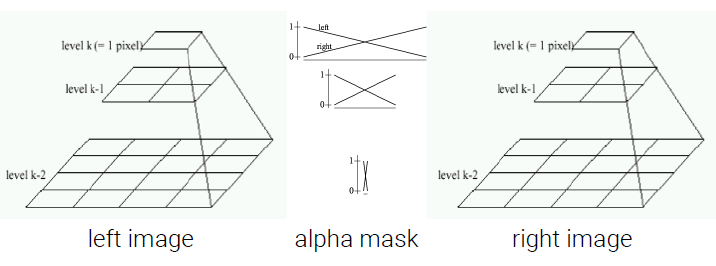 만약 2개의 input image에 scale이 큰 구조물이 있을 때, 이는 low frequency component가 있다는 의미이고 이러한 경우에 seam을 피하고 싶다면 천천히 blending을 하거나 넓은 window를 사용해야 한다. 반대로 2개의 input image에 scale이 작은 구조물에 해당하는 high frequency component가 있을 때는 ghosting을 피하기 위해서 빠르게 blending을 하거나 좁은 window를 사용해야 한다.
만약 2개의 input image에 scale이 큰 구조물이 있을 때, 이는 low frequency component가 있다는 의미이고 이러한 경우에 seam을 피하고 싶다면 천천히 blending을 하거나 넓은 window를 사용해야 한다. 반대로 2개의 input image에 scale이 작은 구조물에 해당하는 high frequency component가 있을 때는 ghosting을 피하기 위해서 빠르게 blending을 하거나 좁은 window를 사용해야 한다.
Low frequency component는 scale이 큰 개체를 가지고 있다는 것을 의미하고, 이 경우에는 넓은 transition window를 사용해서 seam을 피해야 한다. 작은 개체에 대해서는 좁은 transiton window를 사용해서 ghosting을 피해야 한다. 이것이 기본 아이디어이다.
2개의 pyramid가 있을 때, 높은 level은 low frequency에 해당해서 넓은 window를 사용해야 하고, 낮은 level은 high frequency에 해당해서 좁은 window를 사용해야 한다.
Laplacian Pyramid
실제로 blending은 Laplacian pyramid를 이용하게 된다. 구체적으로 첫번째 step에서 각각의 image에 대해서 2개의 Laplacian pyramid를 만들게 된다. 그리고 2번째 step에서는 region mask를 사용해서 pyramid로부터 각각의 level에서 blending을 해준다.
우리는 각각의 level마다 region mask가 필요하고, 이 mask는 alpha mask가 된다. 마지막으로 최종 blended image를 얻기 위해서 pyramid를 겹치면 된다.
Image 2개가 있다고 해보자. 각각의 iamge에 대해서 Laplacian pyramid를 만들 수 있을 것이다. 각각의 level에 대해서 alpha blending을 이용해서 2개의 image를 같이 blending을 진행한다. 그러면 각각의 level에 대해서 1개의 blended image가 나오게 된다. 그러면 Laplacian pyramid로부터 새로운 Gaussian image pyramid를 얻게 될 것이다. 그렇게 새롭게 image pyramid를 만든 것이다. 그리고 이를 계속 더해가면 최종적으로 output을 만들 수 있다.
그렇다면 blending region은 각각의 level마다 얼마나 커야할까? 각 level에서 blending을 할 때 transition area의 크기를 정해줘야 한다. 모든 level에 대해서 scale이 다르더라도 transition area의 크기는 같게 설정해줘야 한다. 만약 5개의 pixel을 transition area로 어느 level에서 사용하고 있다면 다른 level에서도 5개의 pixel을 사용해야 한다. 왜냐하면 우리가 높은 level에서 이미 보았듯이 훨씬 큰 transition area를 사용해야 하지만, 이 image는 이미 작기 떄문에 같은 크기의 transition area를 사용하더라도 상대적으로 훨씬 더 크게 된다. 우리는 low frequency component에 대해서는 더 큰 transition area를 사용하는 것이다. 그래서 모든 level에서 transition area의 크기를 같게해서 사용하는 것이다.
Multi-Band Blending Using Laplacian Pyramid
 이는 multi-band blending의 예시이고, 가장 높은 level의 image를 upsampling해서 크기를 모두 같게 만든 것이다.
이는 multi-band blending의 예시이고, 가장 높은 level의 image를 upsampling해서 크기를 모두 같게 만든 것이다.
 이 예시는 자연스러워보인다. 그래서 눈과 손 사이의 transition area를 찾기가 어렵다.
이 예시는 자연스러워보인다. 그래서 눈과 손 사이의 transition area를 찾기가 어렵다.
Poisson Blending
Poisson blending은 image blending의 기법 중 하나로 poisson이라는 이름은 poisson 식을 사용하기 때문이다.
 2개의 image가 있고 하나는 source image, 다른 하나는 destination image이다. 우리가 하고 싶은 것은 해를 복사해서 물에 반사되도록 복사를 하는 것이다. 만약 단순하게 복사하고 붙여넣으면 image의 밝기가 서로 다르기 때문에 부자연스러운 결과가 된다. 이러한 경우에는 alpha blending을 사용해도 결과가 만족스럽지 않을 것이다. 그래서 사용하는 것이 바로 poisson blending이다. Poisson blending은 source와 destination의 밝기가 다를 때 특별하게 사용이 된다.
2개의 image가 있고 하나는 source image, 다른 하나는 destination image이다. 우리가 하고 싶은 것은 해를 복사해서 물에 반사되도록 복사를 하는 것이다. 만약 단순하게 복사하고 붙여넣으면 image의 밝기가 서로 다르기 때문에 부자연스러운 결과가 된다. 이러한 경우에는 alpha blending을 사용해도 결과가 만족스럽지 않을 것이다. 그래서 사용하는 것이 바로 poisson blending이다. Poisson blending은 source와 destination의 밝기가 다를 때 특별하게 사용이 된다.
 여기서는 곰과 사람을 복사해서 아무도 없는 물에다가 붙여넣고 싶다. 만약 copy-and-paste를 사용해서 단순히 복사해서 붙여 넣으면 물의 색이 다르기 때문에 부자연스러운 결과가 생기게 된다. 이러한 색 문제를 해결하기 위해서도 poisson blending을 사용한다. Poisson blending을 사용하면 자연스러운 결과를 만들 수 있다. Poisson blending을 자동적으로 target image를 따라 밝기나 색을 조절하게 된다.
여기서는 곰과 사람을 복사해서 아무도 없는 물에다가 붙여넣고 싶다. 만약 copy-and-paste를 사용해서 단순히 복사해서 붙여 넣으면 물의 색이 다르기 때문에 부자연스러운 결과가 생기게 된다. 이러한 색 문제를 해결하기 위해서도 poisson blending을 사용한다. Poisson blending을 사용하면 자연스러운 결과를 만들 수 있다. Poisson blending을 자동적으로 target image를 따라 밝기나 색을 조절하게 된다.
Poisson Blending: 1D Example
Possion blending의 주된 아이디어는 다음과 같다.
 Intensity의 평균이 다른 2개의 signal A와 B가 있다고 해보자. 만약 이 둘을 단순히 blending하면 위와 같은 결과를 얻을 것이다. 2개의 signal의 평균값이 다르기 때문에 중간에 intensity가 크게 튀는 부분이 생긴다. 이러한 부분 때문에 blending 결과가 부자연스럽게 된다.
Intensity의 평균이 다른 2개의 signal A와 B가 있다고 해보자. 만약 이 둘을 단순히 blending하면 위와 같은 결과를 얻을 것이다. 2개의 signal의 평균값이 다르기 때문에 중간에 intensity가 크게 튀는 부분이 생긴다. 이러한 부분 때문에 blending 결과가 부자연스럽게 된다.
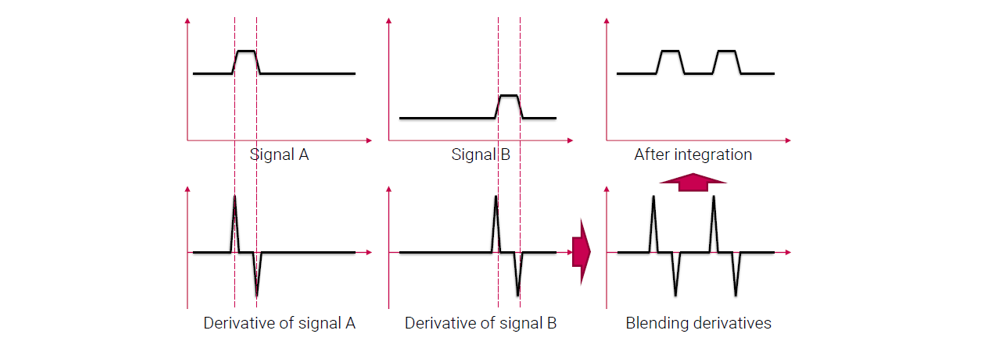 그래서 poisson blending의 주된 아이디어가 위와 같다. 바로 pixel 값이나 intensity 값들을 blending을 하기보다는 2개의 signal로부터 derivative를 먼저 계산해준다. 그리고 2개의 derivative를 합쳐주게되면 평균값이 크게 다르지 않게 된다. Derivative의 평균이 0에 매우 가까워지게 되어서 derivative space에서 더 smooth한 blending 결과를 얻을 수 있다. 이제 이 blending derivative로부터 blending signal을 복원할 수 있다. 즉, 우리는 derivative가 blending 결과와 같은 function을 찾는 것이다.
그래서 poisson blending의 주된 아이디어가 위와 같다. 바로 pixel 값이나 intensity 값들을 blending을 하기보다는 2개의 signal로부터 derivative를 먼저 계산해준다. 그리고 2개의 derivative를 합쳐주게되면 평균값이 크게 다르지 않게 된다. Derivative의 평균이 0에 매우 가까워지게 되어서 derivative space에서 더 smooth한 blending 결과를 얻을 수 있다. 이제 이 blending derivative로부터 blending signal을 복원할 수 있다. 즉, 우리는 derivative가 blending 결과와 같은 function을 찾는 것이다.
Definitions and Notation
그러면 이제 2D image에서는 어떻게 동작하는지 보도록 하자. 이를 위해서 먼저 notation을 정의하고 갈 것이다.
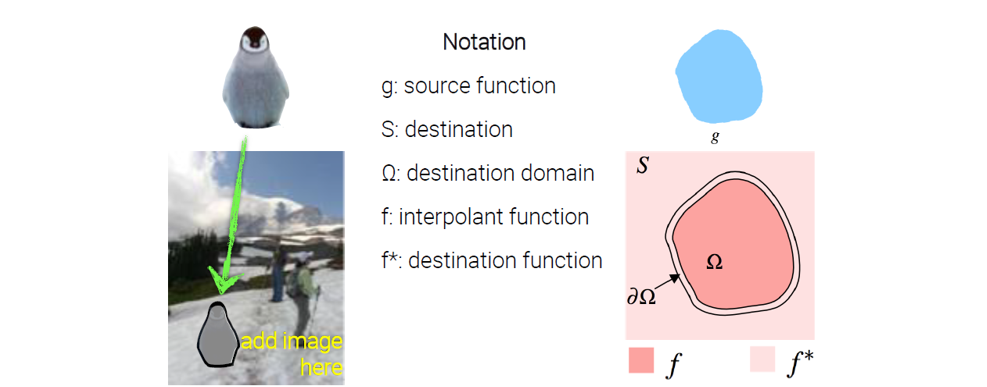 여기서 destination function이 의미하는 것은 destination image에서의 intensity 값을 의미한다. 그리고 destination domain은 destination image에서 우리가 복사한 source image를 붙여넣고 싶은 부분을 말한다. 그리고 는 unknown function으로 우리가 찾고 싶은 것으로 blending 결과에 대응된다. 즉, 는 poisson blending 결과 foureground region의 pixel 값이다. 그래서 우리는 poisson blending을 한 결과로부터 source region의 pixel 값을 찾고 싶은 것이다. 그리고 이 pixel 값들은 자연스러운 결과를 보여야하고, foreground와 background 사이의 seam이 보이지 않아야 한다.
여기서 destination function이 의미하는 것은 destination image에서의 intensity 값을 의미한다. 그리고 destination domain은 destination image에서 우리가 복사한 source image를 붙여넣고 싶은 부분을 말한다. 그리고 는 unknown function으로 우리가 찾고 싶은 것으로 blending 결과에 대응된다. 즉, 는 poisson blending 결과 foureground region의 pixel 값이다. 그래서 우리는 poisson blending을 한 결과로부터 source region의 pixel 값을 찾고 싶은 것이다. 그리고 이 pixel 값들은 자연스러운 결과를 보여야하고, foreground와 background 사이의 seam이 보이지 않아야 한다.
이러한 notation 중에서 가 우리가 찾고 싶은 unknown function이고, 어떻게 이 를 찾아야 하는 것일까? Function 는 다음의 조건을 만족해야 한다.
- 의 derivative는 에 있는 의 derivative와 비슷해야 한다. 의 derivative는 source function과 비슷해야 한다.
- 밖의 영역에서 의 pixel 값이 pixel 값과 비슷해야 한다. 만약 오직 안과 boundary를 따라 pixel 값을 포함하기 위해서 unknown을 설정한다면, 는 안과 boundary에서 pixel 값을 포함하게 된다. 그리고 의 boundary에 있는 pixel 값에 대해서 우리는 이 값들이 가능한 의 pixel 값과 비슷해지기를 원한다. 그리고 안에서 의 pixel 값의 derivative가 가능한 의 pixel 값의 derivative만큼 가까워지기를 원한다.
Interpolation Criterion
이러한 조건들을 기반으로 우리는 문제를 다음과 같이 수식으로 정리할 수 있다.
 의 gradient와 에 있는 를 최소화하기를 원한다. 여기서 는 source image의 gradient이다. 그리고 boundary를 따라서 는 boundary에 있는 와 같은 pixel 값을 가져야 한다. 여기서 는 destination image의 pixel 값이다. 이러한 hard constraint를 가지고 우리는 에 관해서 최소화 할 수 있고, poisson image blending 결과를 찾을 수 있다.
의 gradient와 에 있는 를 최소화하기를 원한다. 여기서 는 source image의 gradient이다. 그리고 boundary를 따라서 는 boundary에 있는 와 같은 pixel 값을 가져야 한다. 여기서 는 destination image의 pixel 값이다. 이러한 hard constraint를 가지고 우리는 에 관해서 최소화 할 수 있고, poisson image blending 결과를 찾을 수 있다.
그래서 이러한 종류의 문제는 "variational" problem이라고 부르고, 여기서 variational이라는 것은 unknown이 전체 함수인 경우에 대한 optimization을 의미한다.
Variational problem을 최소화하는 것은 의 gradient가 의 gradient처럼 보여야 한다. 또한 는 boundary를 따라서 와 같아야 한다. 이 문제를 풀게 되면 우리는 poisson problem의 해를 찾게 된다. 그러면 어떻게 풀어야 할까?
Equivalently
이 optimization problem을 푸는 것은 poisson equation을 푸는 것과 똑같고, poisson equation은 다음과 같다.
 이 식을 푸는 것은 varitional problem을 최소화하는 것과 같다. 그리고 주어진 조건을 dirichlet boundary condition이라 한다. Poisson equation이 의미하는 것은 의 Laplacian이 의 Laplacian과 같아야한다는 것을 의미한다.
이 식을 푸는 것은 varitional problem을 최소화하는 것과 같다. 그리고 주어진 조건을 dirichlet boundary condition이라 한다. Poisson equation이 의미하는 것은 의 Laplacian이 의 Laplacian과 같아야한다는 것을 의미한다.
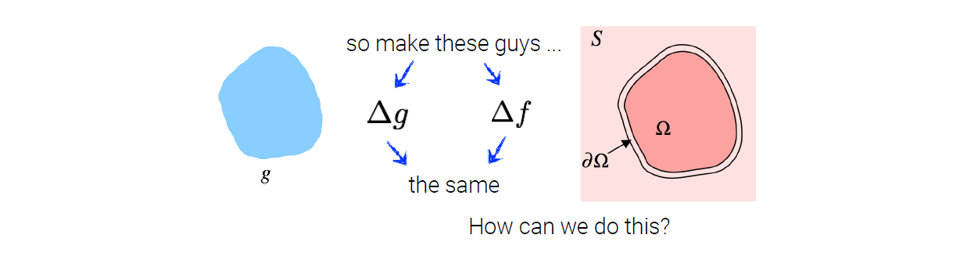 위에서 Laplacian들을 같게 만드는 를 찾음으로써 우리는 blending image 를 찾을 수 있다.
위에서 Laplacian들을 같게 만드는 를 찾음으로써 우리는 blending image 를 찾을 수 있다.
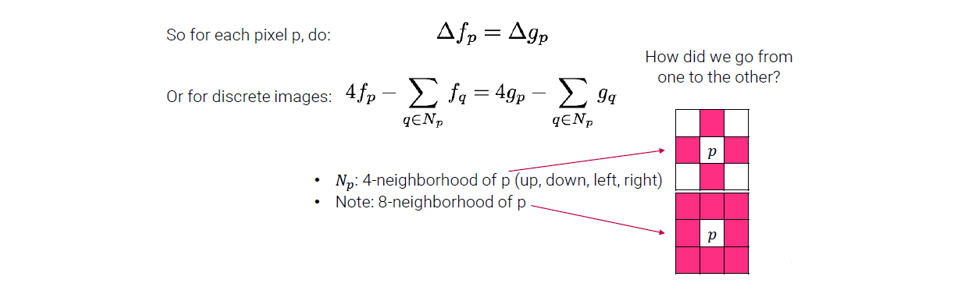 그래서 각 pixel 에 대해서 우리는 위와 같은 식을 가지게 되고, 의 divergence가 정확히 의 Laplacian과 같아지게 된다. 왜냐하면 의 정의 때문이다. 그래서 각 pixel에 대해서 위와 같은 식을 가지게 되고 이를 만족하는 를 찾아야 한다. 그리고 poisson equation은 continuous domain에서 정의되지만, image blending은 discrete image에 대한 것이다. 그래서 우리는 discrete 버전으로 poisson equation을 이끌어 낼 수 있다. 여기서 는 4개의 이웃을 나타내고, 이는 상하좌우에 대응되는 4개의 pixel을 말한다. 그리고 또한 8개의 이웃도 정의할 수 있다. 이렇게 8개의 pixel을 8-neighborhood라고 부른다. 우리는 쉽게 discrete poisson equation을 로부터 finite different method를 이용해서 이끌어낼 수 있다.
그래서 각 pixel 에 대해서 우리는 위와 같은 식을 가지게 되고, 의 divergence가 정확히 의 Laplacian과 같아지게 된다. 왜냐하면 의 정의 때문이다. 그래서 각 pixel에 대해서 위와 같은 식을 가지게 되고 이를 만족하는 를 찾아야 한다. 그리고 poisson equation은 continuous domain에서 정의되지만, image blending은 discrete image에 대한 것이다. 그래서 우리는 discrete 버전으로 poisson equation을 이끌어 낼 수 있다. 여기서 는 4개의 이웃을 나타내고, 이는 상하좌우에 대응되는 4개의 pixel을 말한다. 그리고 또한 8개의 이웃도 정의할 수 있다. 이렇게 8개의 pixel을 8-neighborhood라고 부른다. 우리는 쉽게 discrete poisson equation을 로부터 finite different method를 이용해서 이끌어낼 수 있다.
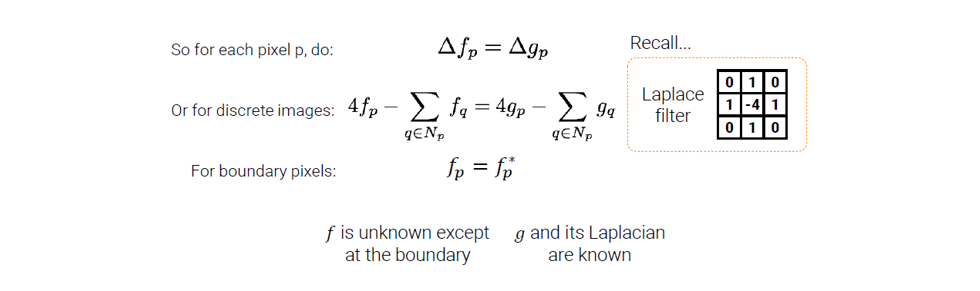 그래서 discrete 버전이 Laplacian filter를 이용해 유도되고, second-order derivative filter인 Laplacian filter은 위와 같다. Discrete 버전의 식은 자세히보면 단순히 의 linear combination이고, 로 표현될 수 있다. 여기서 은 Laplacian filter이고, continuouse eqauation에서 Laplacian operator의 finite different version이다. Discrete boundary condition에서 를 정의할 수 있다. 그리고 이는 hard constraint이다.
그래서 discrete 버전이 Laplacian filter를 이용해 유도되고, second-order derivative filter인 Laplacian filter은 위와 같다. Discrete 버전의 식은 자세히보면 단순히 의 linear combination이고, 로 표현될 수 있다. 여기서 은 Laplacian filter이고, continuouse eqauation에서 Laplacian operator의 finite different version이다. Discrete boundary condition에서 를 정의할 수 있다. 그리고 이는 hard constraint이다.
우리의 목적은 모든 pixel에 대해서 위의 식들을 만족하는 를 찾는 것이다. Discrete poisson equation은 에서 만족해야 한다. 더불어서 은 boundary를 따라 만족해야 한다. 이는 그저 linear equation이고 는 각 pixel 에 대해서 scalar 값이다. 만약 우리가 grayscale image를 가정한다면 이 식을 함께 모아서 linear system으로 만들 수 있다.
Solving the Linear System
여기서 는 다음과 같이 정의 된 vector이다.
각 element는 1개의 pixel 위치에 있는 1개의 pixel 값에 대응한다. 그리고 에서 1개의 row는 discrete poisson equation의 좌변에 의해서 결정된다. 그 결과 는 discrete poisson equation의 우변에 의해서 결정이 된다. 그 결과 우리는 커다란 linear system을 가지게 되고 에 대해서 linear system을 풀게되면 우리는 poisson blending image를 가지게 될 것이다.
Contrast Problem
Poisson blending이 자연스럽게 보이는 강력한 blending 기술이지만 contrast problem이라 불리는 문제가 한가지 존재한다.
 이는 contrast problem을 보여주는 예시이다. 2개의 source image가 있을 때, 곰을 물과 blending하고 싶다. 단순히 poisson blending을 적용하게되면 결과는 우측과 같다. 곰이 contrast를 잃어서 부자연스럽게 보이게 된다. 이렇게 contrast를 잃는 것은 어두운 image를 밝은 이미지에 blending 하려고 할 때 종종 일어난다. 왜냐하면 contrast가 multiplicative property이기 때문인데, 이것이 의미하는 것은 어두운 지역에서 우리는 intensity difference를 더 분명하게 인식할 수 있다.
이는 contrast problem을 보여주는 예시이다. 2개의 source image가 있을 때, 곰을 물과 blending하고 싶다. 단순히 poisson blending을 적용하게되면 결과는 우측과 같다. 곰이 contrast를 잃어서 부자연스럽게 보이게 된다. 이렇게 contrast를 잃는 것은 어두운 image를 밝은 이미지에 blending 하려고 할 때 종종 일어난다. 왜냐하면 contrast가 multiplicative property이기 때문인데, 이것이 의미하는 것은 어두운 지역에서 우리는 intensity difference를 더 분명하게 인식할 수 있다.
2개의 image가 있다고 해보자. 하나의 image는 전반적으로 낮은 intensity를 가지고 있고 그 중에서도 일부분이 더 낮은 경우이고, 다른 image는 전반적으로 높은 intensity를 가지고 있고 그 중에서도 일부분이 더 높은 경우이다. 각각의 image에 대해서 intensity의 difference를 구해서 contrast를 찾을 수 있다. 비록 두 image에서의 contrast가 정확하게 같을지라도 전반적인 경향이 달라서 우리의 눈에는 다르게 보인다. 우리는 어두운 image에 대해서 더 분명하게 차이를 인식할 수 있다. 반면 밝은 image에 대해서는 같은 contrast라 할지라도 그 차이가 희미하게 인식이 된다. Gradient의 크기가 blending의 결과와 어두운 source image와 같을 것이다. 같은 크기의 derivative에도 불구하고 blending 결과가 더 희미하게 보이게 된다.
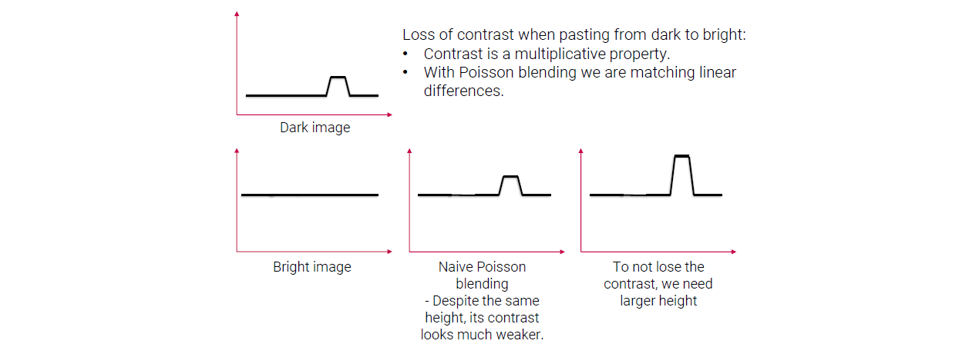 어두운 image와 밝은 image가 있다고 해보자. Naive poisson blending을 하게 되면 중앙의 결과를 얻게 된다. 이 결과와 어두운 image를 비교했을 때, intensity의 높이차가 같다고 할지라도 blending 결과가 더 희미하게 보일 것이다. Contrast를 잃지 않기 위해서 poisson blending 이후에 더 큰 높이차를 가질 필요가 있다. 이는 아무래도 사람의 눈이 그렇게 인식하기 때문이다.
어두운 image와 밝은 image가 있다고 해보자. Naive poisson blending을 하게 되면 중앙의 결과를 얻게 된다. 이 결과와 어두운 image를 비교했을 때, intensity의 높이차가 같다고 할지라도 blending 결과가 더 희미하게 보일 것이다. Contrast를 잃지 않기 위해서 poisson blending 이후에 더 큰 높이차를 가질 필요가 있다. 이는 아무래도 사람의 눈이 그렇게 인식하기 때문이다.
 해결 방법으로 poisson image blending을 할 때 log domain을 사용할 수 있다. Pixel 값을 바로 사용하기 보다는 각 image에 대해서 log transformation을 적용하는 것이다. 그리고 poisson blending 이후에 exponential function을 사용해서 원래의 pixel domain으로 복원시키는 것이다. 그러면 결과적으로 더 선명한 image를 얻을 수 있다.
해결 방법으로 poisson image blending을 할 때 log domain을 사용할 수 있다. Pixel 값을 바로 사용하기 보다는 각 image에 대해서 log transformation을 적용하는 것이다. 그리고 poisson blending 이후에 exponential function을 사용해서 원래의 pixel domain으로 복원시키는 것이다. 그러면 결과적으로 더 선명한 image를 얻을 수 있다.
More Blending
 Poisson blending 결과가 copy-paste 결과보다 더 자연스러운 것을 볼 수 있다.
Poisson blending 결과가 copy-paste 결과보다 더 자연스러운 것을 볼 수 있다.
Blending Transparent Objects
 또 다른 예시로 source image와 destination이 있을 때, blending 결과이다.
또 다른 예시로 source image와 destination이 있을 때, blending 결과이다.
Editing
 Poisson equation은 blending뿐만 아니라 image editing에도 사용이 된다. 예를 들어 image의 gradient를 조작해서 image의 색을 바꿀 수 있다.
Poisson equation은 blending뿐만 아니라 image editing에도 사용이 된다. 예를 들어 image의 gradient를 조작해서 image의 색을 바꿀 수 있다.
Concealment
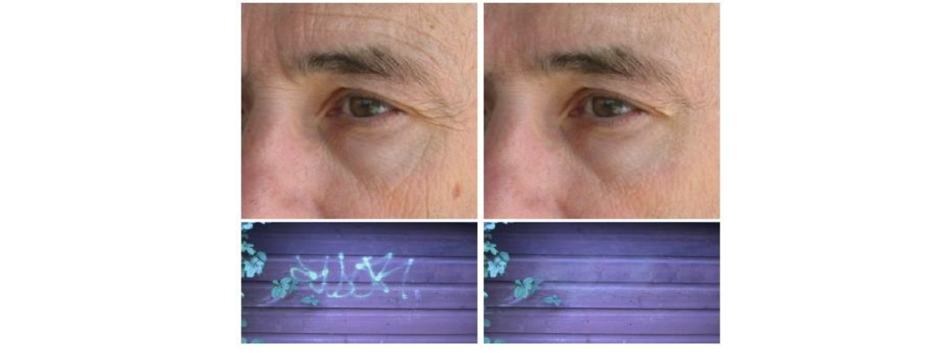 Image 상에서 gradient를 제거함으로써 주름이나 다른 구조를 없앨 수 있다. 우리는 image로부터 derivative를 계산할 수 있고, 이후 이를 0으로 만들어 제거할 수 있다.
Image 상에서 gradient를 제거함으로써 주름이나 다른 구조를 없앨 수 있다. 우리는 image로부터 derivative를 계산할 수 있고, 이후 이를 0으로 만들어 제거할 수 있다.
Texture Swapping
 Poisson image editing은 질감을 바꾸는데도 사용이 된다. Derivative나 gradient를 계산해서 gradient를 바꾸어 복원하면 된다.
Poisson image editing은 질감을 바꾸는데도 사용이 된다. Derivative나 gradient를 계산해서 gradient를 바꾸어 복원하면 된다.

와우! 잘봤습니다