[계산사진학] Multiresolution Processing

Multiresolution Processing

서로 다른 크기의 얼굴이 포함되어 있는 image를 가지고 있다고 해보자. 이렇게 크기가 다른 얼굴을 검출하기 위해서 우리는 multiresolution processing을 사용할 수 있다.

Mutliresolution processing은 또한 개체를 찾는데 있어서 빠른 속도로 찾을 수 있도록 도와줄 수 있다. 크기가 큰 image에서 개체를 locating거나 개체의 bounding box를 찾는 것은 쉽지 않다.
예를 들어 우측과 같이 image가 있고 좌측에는 template image가 있다고 해보자. 우리는 우측 image에서 template image의 위치를 찾고 싶다.
위치를 찾기 위해서 가장 간단한 방법은 direct search이다. 이 방법은 sliding window를 좌측 상단부터 우측 하단으로 이동시켜서 pixel 값을 하나씩 비교하는 방식이다. 그러나, 이 방법은 특히 image의 크기가 커지게 되면 computationally expensive하다.
그래서 direct search 대신 multi-scale search를 사용할 수 있다. 이 방법은 2개의 image를 동시에 downsampling 하면 pixel의 수가 급격히 줄어들기 때문에 computational cost를 크게 줄일 수 있다. 왜냐하면 이렇게 줄이면 sliding window 수도 줄어들게 되고 downsampled patch의 pixel 수도 줄어들게 되기 때문이다. 그래서 훨씬 더 빠르게 template image와 같은 image 상의 위치를 찾을 수 있다. Image가 downsample 되었기 때문에 정확한 pixel-level 상의 위치를 찾는 것은 어려워졌다. 그래서 고해상도 image에서 저해상도 image로부터 예측된 위치를 통해서 정확한 위치를 찾을 수 있다.

예를 들어 downsampled template patch를 downsampled image로부터 찾을 수가 있지만, 원래 image에서 원점 주변을 search함으로써 고해상도 image에서 window를 더욱 세분화할 수 있다. Downsampled image에서 찾은 bounding box가 원래 고해상도 image 상에서는 살짝 어긋날 수 있다. Image를 downsampling하면 정확한 위치를 찾는 것은 어렵다. 이런 경우 우리는 그 주변을 search하면서 쉽게 위치를 개선할 수 있다. 이때 downsampled image를 사용하지 않는다면 고해상도 image에서 모든 region을 search 해야한다. 그러나 이미 대략적인 위치를 찾았기에 살짝 어긋나더라도 그 주변만 search하면 되는 것이다.

Multiresolution processing은 또한 image blending이나 image restoration과 같은 다른 image processing task들에도 유용하게 사용된다. Image denoising, super resolution, deblurring과 같은 image restoration에서 가장 먼저 작은 scale에서 대략적인 image 구조를 복원한 다음에 더 큰 scale에서 디테일들을 찾게 된다.

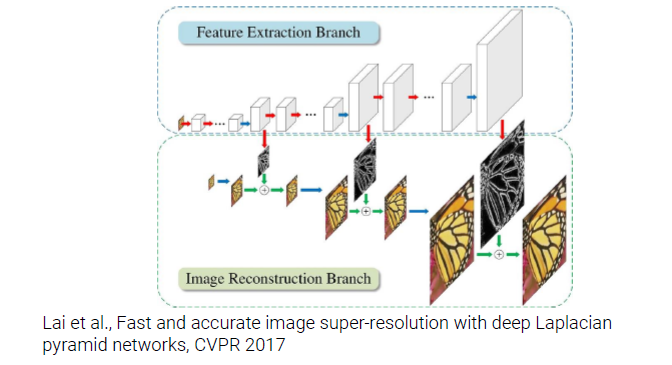이 image는 super-resolution paper에 있는 것이다. Super-resolution 문제는 저해상도 image가 있을 때 이를 고해상도 image로 만드는 것이다. 하나의 저해상도 image를 가지고 있을 때 이를 확대하여 디테일들을 보고싶은 것이다. 저해상도 image는 매우 작은 image이기 때문에 디테일을 가지지 못한다. 그래서 우리는 고해상도 image를 만들기 위해서 어떻게든 모든 디테일들을 찾아내야 한다. 이러한 것이 super-resolution에서의 challenge가 된다.

더 효과적으로 이 문제를 다루기 위해서 multi-resolution processing 아이디어를 사용해야 한다. 저해상도 image를 처음에 크기를 살짝 키우게 되면 더 많은 디테일을 만들 수 있고, 다시 또 크기를 살짝 키우면 다시 디테일을 추가로 만들게 된다. 이러한 식으로 작은 scale에 대해서 image structure을 만들고 큰 scale로부터 좋은 디테일들을 복원하는 것이다.

Downsampling

Multiresolution processing을 하기 위해서는 2개의 근본이 되는 image operation을 사용해야 한다. 하나는 downsampling이고 다른 하나는 upsampling이다.

Downsampling은 2-step으로 진행이 된다. 첫번째 step은 aliasing을 피해기 위해서 Gaussian filter와 같이 low-pass filter를 이용해서 image를 convolution 하는 것이다. 두번째 step은 image의 크기를 줄이기 위해서 r번째 image를 보관하는 것이다. 그래서 적절한 lowpass filter가 없다면 downsampled image에 aliasing이 생길 수 있다. 이러한 과정이 downsampling의 전형적인 방식이지만, convolution 결과의 많은 pixel들이 단순히 사라지기 때문에 불필요한 연산을 초래하게 된다. 그래서 대안으로 computational cost를 줄이기 위해서 모든 r번째 sample의 convolution을 사용하게 된다.

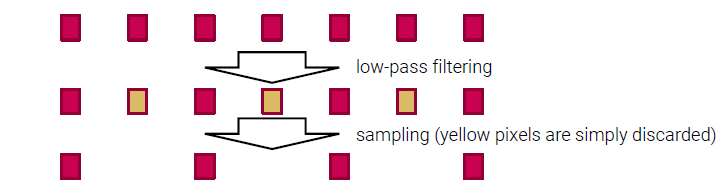이러한 2-step 과정에서 우리는 위에서 노란색과 같은 pixel 값들을 계산해야 한다. 이 방법을 1-step으로 대신해서 진행할 수 있다. 그래서 convolution 결과를 쉽게 계산하여 computational cost를 줄일 수 있다.

Upsampling

두번째 근본이 되는 image operation은 upsampling이다. Upsampling의 목적은 image의 spatial size를 늘리는 것이다.
Upsampling은 보통 interpolation을 이용해서 진행된다.

1D Interpolation

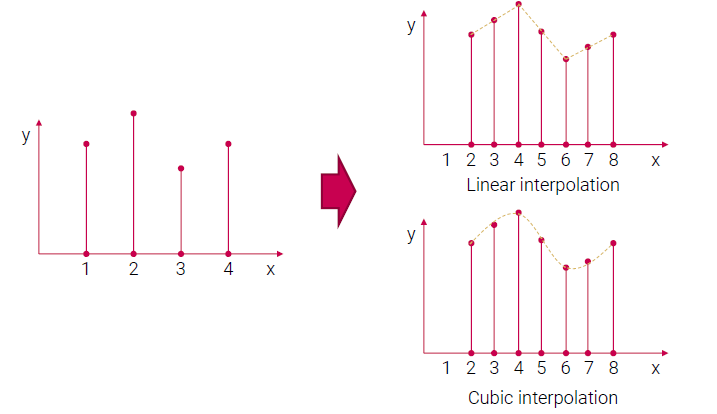먼저 1d interopolation에 대해서 알아보자. 좌측에 4개의 point들이 있다. 그러면 이 4개의 point들에 대해서 우측과 같이 8개의 point들을 얻기 위해서 umsapmling을 할 것이다. Interpolation method로는 linear interpolation과 cubic interpolation이 있다. 물론 이외에도 여러 interpolatino method들이 존재한다.

Linear interpolation은 linear function을 사용한다. 즉, 우리는 point들을 잇는 직선을 그리고 직선 위에 있는 새로운 point들을 sample로 추출한다. 이러한 방식이 linear interpolation이고 cubic interpolation은 cubic function을 사용해서 원래의 point들을 cubic 곡선으로 이어주게 된다. 여기서 cubic function은 여러개의 point들을 이용해서 그려주면 된다. 그리고 마찬가지로 새로운 point들을 sampling한다.

2D Interpolation

이제 1d interpolation을 2차원으로 확장시켜서 bilinear interpolation이나 bicubic interpolation을 할 수 있다. Bilinear interpolation은 point들을 linear surface에 근사하는 방법으로 이는 매우 간단하고 빠르지만, 그 결과는 그리 좋지 못하다. Bilinear interpolation을 진행하면 예상하지 못한 주름 등이 생기기 때문이다.
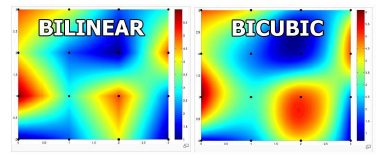Bilinear interpolation이 빠른 이유는 새로운 point를 sampling 하기 위해서 오로지 인접한 4개의 point들만이 사용되기 때문이다.

Bicubic interpolation은 pixel 값 하나를 결정하는데 있어서 bilinear interpolation보다 많은 16개의 point들을 사용한다. 왜냐하면 cubic function을 결정해야 하는데 1d cubic interpolation에서는 4개의 point를 사용했었고, 2차원으로 확장하면서 cubic function을 결정하는데는 더 많은 point가 필요하기 때문이다. 이것이 bicubic interpolation이 bilinear interpolation보다 느린 이유다.

Bicubic interpolation은 cubic interpolation의 확장이고, photo editing package에 있어서 가장 널리 사용되는 interpolation 방법이다. 여기서는 piecewise-cubic spline을 사용해서 더 자연스러운 결과를 이끌어낸다.

(Bilinear) 2x Upsampling Process

Upsampling이 어떻게 동작하는지 자세히 보도록 하자. Bilinear upsampling을 하는 방법 중 하나는 upsampler와 interpolation filter를 이용하는 것이다.
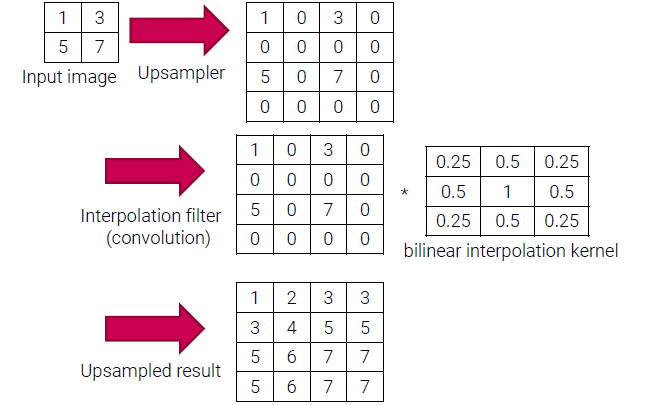$2 \times 2$ input image가 있다고 가정하고, upsampler를 이용해서 input image의 pixel 값으 퍼뜨려서 $4\times4$ image를 만들 수 있다. 정해진 위치에 원래의 pixel 값을 두면 나머지는 0으로 채우게 된다. 그리고 여기에 convolution filter인 interpolation filter를 적용한다. Convolution operation을 통해서 upsampled image를 만들 수 있다.

Bilinear interpolation에서는 $3\times 3$ filter를 필요로 한다. 반면 bincubic interpolation에서는 $5\times5$ filter를 필요로 해서 더 나은 결과를 만들어내지만, computational cost가 expensive하다는 단점도 있다.

Different Interpolation Filters

다음은 서로 다른 interpolation method를 이요한 결과이다.
Nearest neighbor interpolation은 bilinear interpolation보다도 간단하다. 단순히 가장 가까운 pixel 값을 복사해서 사용하기 때문에 결과가 그리 좋지 못하다. 그래서 사실 여기에는 interpolation이 없다고 봐도 무방하다.

여기 또 다른 예시가 있다. Bilinear interpolation은 꽤 blurry한 결과를 나타낸다. 반면 다른 결과들은 비록 computational cost가 expensive 하더라도 더 나은 것을 볼 수 있다. 여기서 nine taps라는 것은 $9\times9$ interpolation filter를 의미한다.

Image Pyramids

Image pyramid는 powerful하지만 1개의 해상도 이상의 image를 나타내는데 있어서 개념적으로 간단한 구조를 가지고 있다. Image pyramid는 서로 다른 fequent component들로 image를 분해하는 또 다른 방법으로 사용될 수 있다. 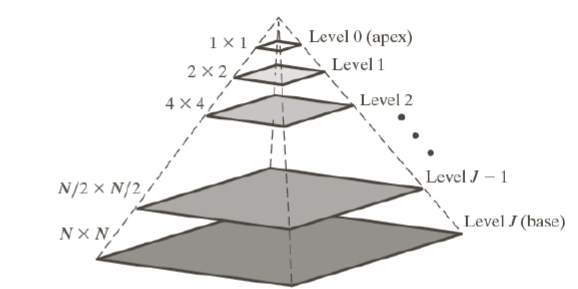Image pyramid에서는 low frequency component가 포함된 결과가 높은 level에 해당하게 된다. 낮은 level로 갈수록 low frequency와 high frequency를 함께 포함하게 된다. 완전히 채워진 pyramid는 $2^J\times2^J$에서 $2^0\times2^0$까지 $J+1$ 해상도 level로 구성됩니다.

그러나 대부분의 경우에서 모든 level를 사용하지는 않는다. 왜냐하면 낮은 level은 너무 적은 정보를 가지고 있기 때문이다. 예를 들어 첫번째 level에서는 1개의 pixel을 가지는데, 사실 1개의 pixel은 유용하게 사용되기 어렵다. 그래서 보통은 낮은 level은 자르고 나머지 부분만 사용하는 경우가 대부분이다.

Gaussian & Laplacian Pyramids

많이 사용되는 pyramid가 2개 있다. 하나는 Gaussian pyramid이고 다른 하나는 Laplacian pyramid이다.

Gaussian Pyramid

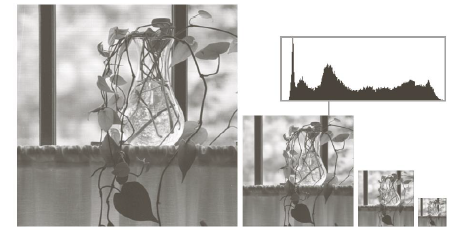Gaussian pyramid에서 원래 image의 downsampling을 한 결과를 여러 level에 걸쳐서 사용한다. 모든 image가 보기에는 똑같지만, 이들의 scale은 전부 다르다.

Laplacian Pyramid

Laplacian pyramid는 Gaussian pyramid와 비슷하게 여러 level에 걸쳐서 image를 나타내지만, 각각의 level에서 scale이 다른 residual image를 사용한다는 특징이 있고 마지막 level에서만 똑같은 image를 사용한다.

Frequency의 관점으로 이야기하면 Gaussian pyramid의 각각의 scale은 low frquency와 high frequency information을 둘 다 가지게 된다. 반면, Laplacian pyramid의 경우 대부분 high frequency information만을 가지게 되고, low frequency information은 가지지 않게 된다.

Constructing a Laplacian Pyramid

이제 더 나은 이해를 위해서 Laplacian pyramid를 어떻게 만드는지 볼 것이다.
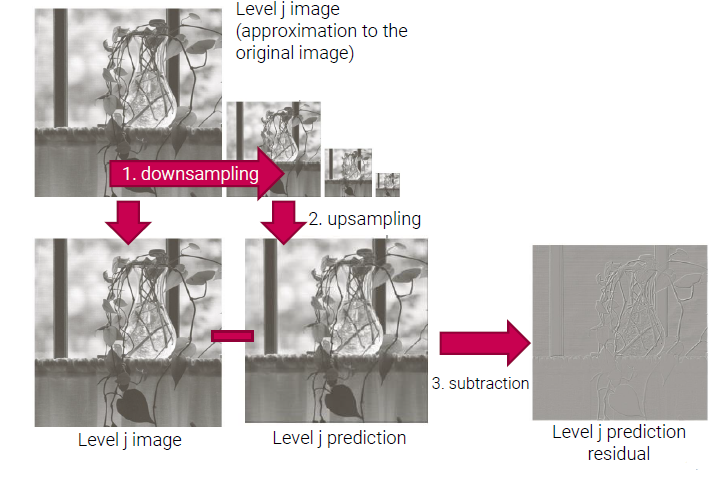우리는 Laplacian pyramid를 Gaussian pyramid로부터 만들 수 있다. 먼저 Gaussian pyramid가 있다고 해보자. Gaussian pyramid의 각각의 level에서 더 작은 image를 만들기 위해서 downsampling이 적용될 것이다. 그리고 다시 이를 upsampling해서 이전의 크기와 같게 만들어준다. 우리가 $J-1$ level에서 downsampling과 upsampling을 진행해서 $J$ prediction을 만들었다고 했을 때, $J$ image와의 difference를 구하게 된다. 그러면 그 결과 residual image를 얻을 수 있다. 이러한 방식으로 모든 level에서 서로 다른 scale의 residual image를 얻으면 된다. 이렇게 Laplacian pyramid를 만들면 된다.

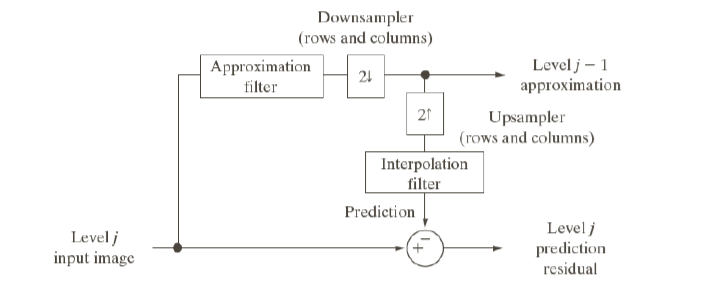Laplacian pyramid를 만드는 과정을 대략 나타내는 diagram이다. Level $j$의 input image가 있다고 해보자. Input image에 Gaussian filter와 같은 lowpass filter인 approximation filter를 적용하고 downsampler를 적용해서 level $j-1$ approximation을 얻을 수 있다. 그리고 downsampled image에 upsampler와 interpolation filter를 적용해서 다시 이전 크기의 upsampled image를 얻을 수 있다. 마지막으로 level $j$의 input image와 upsampled image의 difference를 통해서 prediction resiual image를 구할 수 있다.

이 diagram에서 upsampling process는 2-step으로 이루어져 있고, upsampler와 interpolaition을 사용하는 것이 하나의 방법인 것이다.

From Laplacian to Gaussian

Gaussian pyramid를 통해서 Laplacian pyramid를 만드는 방법을 알아보았다. 반대로 Gaussian pyramid를 Laplacian pyramid를 통해서 만들 수도 있다.
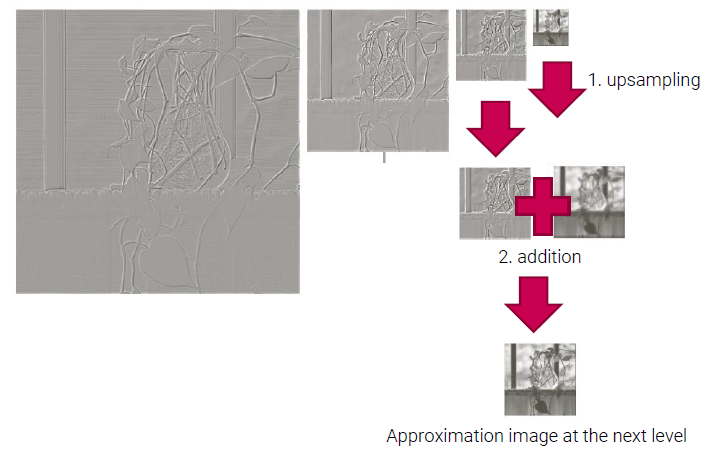Laplacian pyramid에서 모든 level에 대해서 residual image를 가지고 있다. 그러나 마지막 image는 원래 image를 가지게 된다. 이 정보를 이용해서 low frequency component를 사용하게 되는 것이다. 이 image를 upsampling을 해주고 upsampled image와 이전 scale의 residual image를 덧셈 연산을 해준다. 그러면 다른 scale의 approximation image를 얻을 수 있다. 이렇게 모든 level에 대해서 approximation image를 만들어 나가서 Gaussian pyramid를 만들면 된다.

Gaussian and Laplacian Pyramids

Gaussian pyramid와 Laplacian pyramid는 서로 다른 성질을 가지고 있다. Gaussian pyramid의 각각의 level은 원래 image에 대한 approximation을 서로 다른 해상도로 가지고 있다. 반면, Laplacian pyramid의 각각의 level은 prediction residual을 가지고 있다.

Frequency의 관점으로 Gaussian pyramid의 각각의 level은 현재 level에 대응되는 high frequency와 더 높은 level에 대응되는 low frequency를 모두 가지고 있다. 반면, Laplacian pyramid의 각각의 level은 오직 현재 level에 대응되는 high frequency information만 가지게 된다. 그래서 Laplacian pyramid가 각각의 level이 적은 양의 information만 가지게 되어 더 효율적으로 code화 되어 있다. 그래서 Laplacian pyramid는 information을 저장하고 보내는데 더 효과적으로 사용된다.