[계산사진학] Image Synthesis & Generation - DNN Based Style Transfer

Style & Contents

Style transfer는 texture transfer와 거의 유사하다. Style transfer에서는 image를 style과 content의 조합으로 생각한다. 사실 style과 content라는 것을 정의하는데는 모호한 부분이 있다. 무엇이 style이고 무엇이 content인지 명확하게 정의하기는 다소 어렵다. 대략적으로 이야기하자면 content는 image structure라고 생각하면 되고, style은 어떻게 이 structure가 rendering 되고 texturing 되는지라고 생각하면 된다. 사실 style이라는 것은 texture와 거의 동일하다고 봐도 무방하다.
위의 4개의 image는 모두 동일한 content를 가지고 있다. 모든 image에는 하늘도 있고, 건물도 있으며, 물도 또한 보이고 있다. 그러나 차이점이라고 하면 이들은 서로 다른 texture로 렌더링이 되어있다. 즉, 이들은 서로 다른 style을 가지고 있다.

Style Transfer & Image-to-Image Translation

매우 비슷하지만 전혀 다른 문제 2가지가 존재한다. 하나는 style transfer이고, 다른 하나는 image-to-image translation이다.
Style transfer을 살펴보면 우선 일반적으로 source image와 reference style image가 주어지게 된다. 그리고 style transfer의 결과는 source image의 content와 reference style image의 style을 합친 새로운 image가 된다. 예를 들어, 위와 같이 위와 같이 content image와 style image가 있을 때, style image의 style을 content image에 입히고 싶은 것이다.

Image-to-image translation에서 우리가 원하는 것은 여러 source image와 target image들로부터 source domain에서 target domain으로의 mapping을 찾고싶은 것이다. 이는 마치 domain adaptation problem으로 생각될 수 있다. 서로 다른 domain에서의 image들로부터 mapping function을 찾아야 한다. Style transfer와 비교했을 때 style transfer는 특정 source image와 reference style image를 조합해서 새로운 image를 만들어내는데 비해 image-to-image trnaslation은 여러 image들을 domain으로 묶어서 연결시키는 mapping function을 찾게된다.

Style Transfer

Style transferred image는 content image와 style image의 조합으로 정의가 된다.

Neural Style Transfer

가장 대표적인 style transfer의 연구로는 2016년도에 "Image Style Transfer Using Convolutional Neural Networks"라는 논문에서 발표되었다. 이는 최초로 deep learning을 기반으로 style transfer를 수행한 것이다. 비록 제안된 방법이 deep learning을 기반으로 했다고는 하지만, 실질적으로 이 방법은 optimization-based approach이다. 그래서 이 논문에서는 style transfer problem을 다음과 같이 energy function을 통해서 수식화하여 풀고자 했다.

2개의 input으로 $x_c$는 content image이고, $x_s$는 style image이다. 이 image들이 주어졌을 때 위의 energy function을 최소로 만드는 $y^\ast$를 찾고자 한다. 이 energy function은 content loss와 style loss의 합으로 총 2개의 term으로 구성되어 있다. 2개의 term을 최소로 만들어서 style-transferred result image $y^\ast$를 찾을 수 있다. 이제 어떻게 이 2개의 term이 정의되었는지 보도록 하자.

이 논문에서 제안된 energy function은 위와 같이 2개의 term으로 구성되어 있다. 첫번째 term인 $L_{content}(x_c,y)$을 최소로 만들게 되면 $x_c$와 동일한 content를 가지는 result image $y$를 얻을 수 있다. 이를 위해서 다음과 같이 $x_c$와 $y$ 사이의 distance를 이용해서 정의할 수가 있다. 정확히는 $x_c$와 $y$의 content의 distance를 이용하는 것이다. 이들의 distance를 최소로 만들게 되면 $x_c$와 동일한 content를 가지는 $y$를 얻을 수 있게 된다.

두번째 term인 $L_{style}(x_s,y)$을 최소로 만들게 되면 $x_s$와 동일한 style을 가지는 $y$를 얻을 수 있다. 이번에도 $L_{content}$와 유사하게 식을 정의할 수 있다. $x_s$와 $y$의 style의 distance를 정의해서 사용한다.

이렇게 energy function을 정의하게 되면 직관적이고 깔끔하게 받아들일 수 있게 된다. 2개의 term을 최소로 만들어서 $x_c$와 동일한 content를, $x_s$와 동일한 style을 가지는 $y^\ast$를 찾을 수 있다. 이 문제를 풀기 위해서 중요한 것은 content representation과 style representation이다.

Content Representation

어떻게 image의 content representation을 정의할 수 있을까? 이 논문에서 제안한 주된 아이디어는 DNN의 higher layer가 image structure(content)를 잘 포착한다는 것이었다.
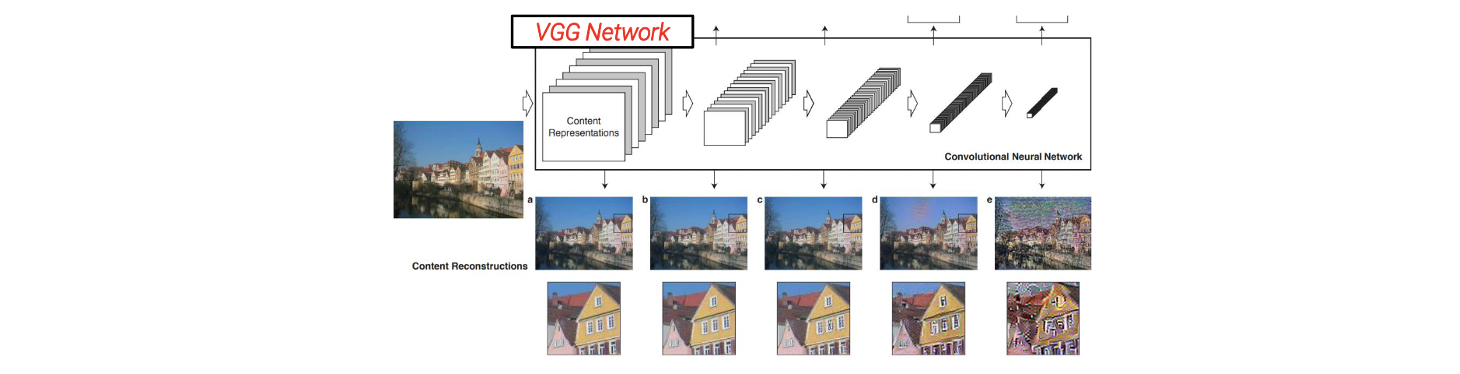예를 들어 image와 VGG network가 있다고 해보자. VGG network는 image classification 문제를 풀기 위해서 제안된 network이다. 흔히 image에서 classification을 하고자 할 때 CNN을 사용해서 image의 content를 설명하는 feature를 추출하곤 한다. 추출이 된 feature들을 기반으로 MLP와 같은 classifier network를 사용해서 image를 어떠한 class로 구분할 수 있게 된다.

CNN을 사용해서 feature를 추출할 수 있고, 이때 여러 layer를 사용하게 된다. 첫번째 layer에서는 보통 low-level feature를 추출하게 된다. 이때, convolution operation을 사용해서 edge 등을 검출할 수가 있다. CNN에서는 여러개의 convolution layer들을 가지고 있어서 input image와 가까운 layer 단계에서는 1개 혹은 2개의 convolution operation을 사용하여 오로직 edge와 같은 low-level feature를 검출하게 되고, 계속해서 convolution operation을 적용하면 창문이 있는지, 차가 있는지 등 디테일한 정보들의 high-level feature를 검출할 수 있게 된다. 이후 이러한 모든 정보를 종합하게 되면 input image의 class를 구분할 수 있게 된다.

Image를 보면 하늘, 건물, 나무 등 여러 개체들로 구성되어 있다. VGG network를 사용하면 여러 convolution layer를 통과시키면서 정보들을 줄일 수가 있다. 그래서 계속 통과시키다보면 나중에는 high-level feature만을 검출하게 되는 구조이다. 이는 image structure 혹은 content의 정보를 가지고 있게 되지만, texture나 style 등의 low-level feature를 가지고 있지 않게 된다. 그래서 higher layer로 가게 되면, image structure 정보만이 남게 된다. 이러한 내용들을 기반으로 이 논문에서는 contente representation을 layer $l$에서 feature map $F^l$로 정의하고자 했다. $l$은 충분히 큰 index이다. 즉, 어느정도 convolution operation을 진행했을 때 쯤의 feature map을 content representation으로 사용하고자 한 것이다.

Style Representation

이번에는 image의 style representation을 정의할 것이고, 이를 위해서 gram matrix를 사용하고자 한다. 주어진 image $x$의 style representation은 다음과 같이 정의가 된다.

여기서 $G^l$은 size가 $N_l\times N_l$인 gram matrix로 정의가 된다. $N_l$은 채널의 크기이다. $G^l$은 VGG network의 feature map을 사용해서 정의가 된다. Image $x$가 있다고 했을 때 이를 VGG network에 집어 넣어서 feature map $F^l$을 얻을 수 있다. 여기서 $l$은 layer의 index이다. $F^l$에서 $C$개의 채널이 있다고 했을 때 $i$번째 채널과 $j$번째 채널을 뽑을 수 있다. 각 채널은 다음과 같이 $F^l_i, F^l_j$로 나타낼 수 있다.

각 채널은 feature value의 2차원 array이고, 우리는 spatial position index를 $k$로 정의할 수 있다. 즉, 2차원 map에서 특정 한 부분을 $k$라고 정의하는 것이다. Gram matrix는 $i,j$ 채널의 $F^l$의 dot product로 정의된다.

이렇게 gram matrix가 정의가 되고, 서로 다른 feature 사이의 correlation을 포착할 수 있다. 이것이 의미하는 무엇일까? 서로 다른 feature 채널은 보통 서로 다른 convolution operation 혹은 filter로 정의가 된다. 예를 들어 image가 있고 2개의 sobel filter가 있다고 해보자. 각 sobel filter는 하나는 수직 방향, 다른 하나는 수평 방향으로 되어 있고 이를 하나씩 적용하게 되면 2개의 다른 image를 얻게 된다. 하나는 vertical edge만을 나타내고 다른 하나는 horizontal edge만을 나타낼 것이다. 이 image들을 합치면 결국에는 feature map을 만들어내게 된다. 이러한 방식이 neural network가 동작하는 방식이다. 이와 같이 서로 다른 feature 채널은 서로 다른 filter kernel에 의해서 정의된다. 그래서 서로 다른 feature 채널은 결국에는 서로 다른 local structure를 포착하게 된다.

주어진 image로 부터 멀리 떨어진 layer에서도 여전히 서로 다른 kernel을 사용할 수 있어서 서로 다른 local structure를 검출할 수 있게 된다. 예를 들어서 위와 같이 가장 좌측에 별이 그려진 image가 있다고 해보자. 하나의 feature 채널을 이용한다고 하면 input image로부터 중간과 같은 structure를 검출할 수 있을 것이다. 그리고 다른 feature 채널을 이용한다고 하면 우측과 같은 structure를 검출할 수 있게 된다. 그래서 convolution neural network는 이러한 방식으로 동작하게 된다.

각 feature map에서는 서로 다른 패턴을 검출할 수 있게 된다. 그래서 별 모양의 반복되는 패턴이 주어졌을 때 각 채널은 완전한 별 모양이 아닌 서로 다른 부분적인 패턴만을 검출하게 된다. 그리고 이 feature map들 사이의 correlation이 있다고 보게 되면 서로 다른 feature map은 함께 나타나게 된다. 그래서 우리는 부분적인 별 모양을 나타내는 feature map 사이에는 어떠한 조합이 있다고 말할 수 있고, 이 패턴들은 항상 같이 나타나서 결국에는 반복되는 완전한 별 모양을 검출할 수 있게 된다. 이는 곧 image의 style을 정의하는 것과 같은 맥락이다. Style은 결국 feature들이 여러가지 형태로 존재한다고 했을 때 통계적으로 가장 두드러지게 나타나는 패턴을 이야기하고, gram matrix는 이러한 feature들로부터 통계적인 부분을 포착할 수 있는 방법 중 하나이다. 서로 다른 feature들 사이의 correlation을 계산해서 상대적으로 빈번하게 나타나는 것을 채택한다고 생각하면 된다.

Summary

지금까지 content representation과 style representation에 대해서 알아보았고, 이를 기반으로 energy function 전체를 정의할 수 있다. Style transfer problem을 풀기 위해서 energy function을 최소로 만들 수 있다.
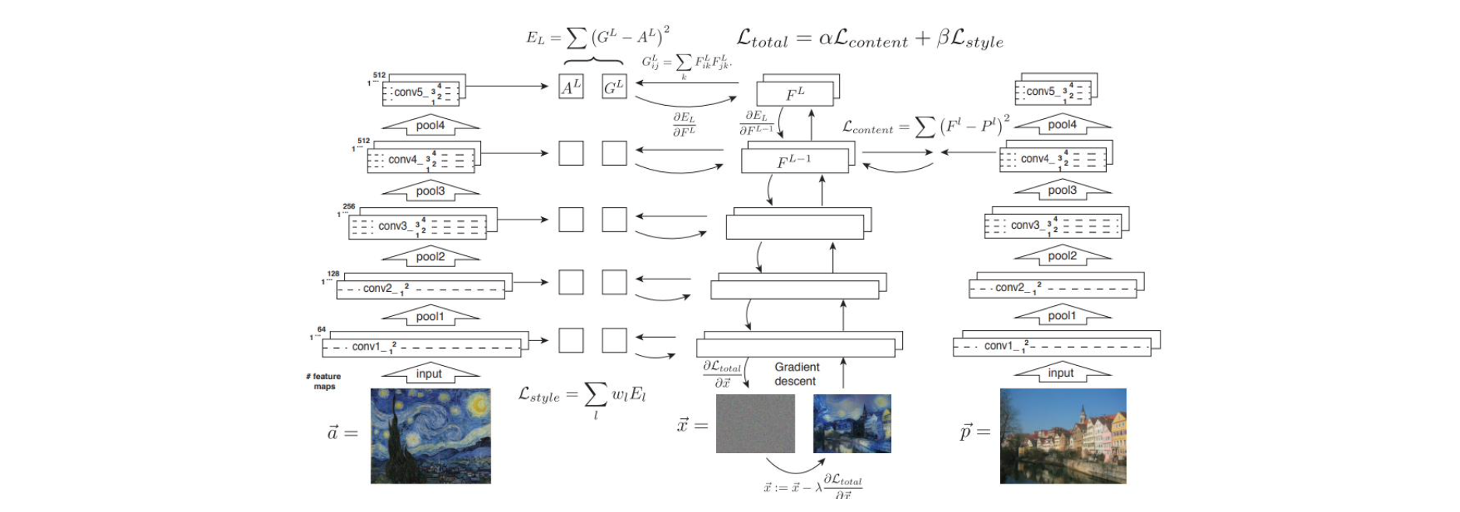예를 들어 style reference image $\vec{a}$와 source image $\vec{p}$가 있다고 해보자. 이 2개의 image를 VGG network에 집어 넣으면 이 image들의 feature map을 구할 수 있게 된다. 여기서 conv4 layer를 $l$-th layer라고 했을 때 $l$-th layer의 feature map을 source iamge의 style representation으로 사용해서 content loss를 정의할 수 있다. 그리고 style reference image의 feature map을 사용하면 위의 예시에서는 총 5개의 gram matrix를 정의할 수 있다. 5개의 layer로부터 5개의 gram matrix $A_1,A_2,\dots,A_5$를 구할 수가 있다.

이제 minimization problem을 풀기 위해서 random noise map $\vec{x}$로 initial solution을 설정할 수 있다. 가장 먼저 이 random noise map을 VGG network에 넣어서 다시 각각의 gram matrix를 구할 수 있다. 이를 $G_1,G_2,\dots,G_5$라고 해보자. 그리고 여기 VGG network에서 $l$-th layer에서 content representation $F^l$도 구할 수 있다. 이렇게 모두 구해진 style loss term과 content loss term으로부터 input image를 업데이트 할 gradient를 back-propagation을 사용해서 계산할 수 있다. 이렇게 반복해서 업데이트를 하고 나면 기존의 random noise image를 style transferred result image로 바꿀 수가 있다. 다음은 source image와 여러 style image를 이용해서 style transfer를 적용한 것이다.

Photo Style Transfer

이후 style transfer 연구가 활발해지고 2017년도에 "Deep Photo Style Transfer"라는 논문에서 새로운 방식이 제안되었다. Style transfer를 실제 사진에 적용한 연구이다.
Input image와 reference style image가 있다고 해보자. 이 2개의 image는 모두 카메라를 이용해 얻은 실제 사진들이다. 다만 차이점은 image의 style이 다르다는 것 뿐이다. 여기서 하고자 하는 것은 reference style image의 style을 input image에 옮기는 것이다. 만약 단순하게 neural style transfer를 적용한다면, 결과적으로 일부 구조가 왜곡된 결과를 얻게 될 것이다. 이는 neural style transfer의 특징이 반영된 결과이기 때문이다. 기존의 방법에서는 단순히 흉내만 내는 local structure를 생각하지 않고 style만 옮기는 방식이다. Photo style transfer에서는 local structure에 왜곡이 생기는 것을 원하지 않는다. 이 논문에서는 local structure는 유지하면서 style만 옮기는 방안을 제시했다.

Adaptive Instance Normalization(AdaIN)

또 다른 중요한 연구로는 2017년도에 "Arbitrary Style Transfer in Real-time with Adaptive Insatnace"라는 논문에서 제안했다. 여기서는 batch normalization과 같은 normalization layer를 사용해서 image style transfer의 문제를 해결하고자 했다. Neural style transfer 연구에서는 style이 통계적으로 모든 feature distribution에 의해서 정의되는 것을 볼 수 있었다. 이 아이디어를 기반으로 해서 이 논문에서는 Adayptive instance normalization(AdaIN) layer를 제시했다. AdaIN layer는 다음과 같이 정의가 된다.

$x$는 content input에서 CNN의 feature map, $y$는 style reference input에서의 feature map, $\mu(x)$는 feature의 평균, $\sigma(x)$는 featuer의 표준편차이다. 위의 식을 보면 feature map을 normalization하는 것을 볼 수 있다. 그리고 여기에 $\sigma(y)$를 곱하고 $\mu(y)$를 더함으로써 서로 다른 feature를 모방하기 위해서 feature distribution을 조작할 수가 있다. 이렇게 content input의 distribution을 바꿔서 style reference input의 distribtuion을 따라가게 할 수 있다.

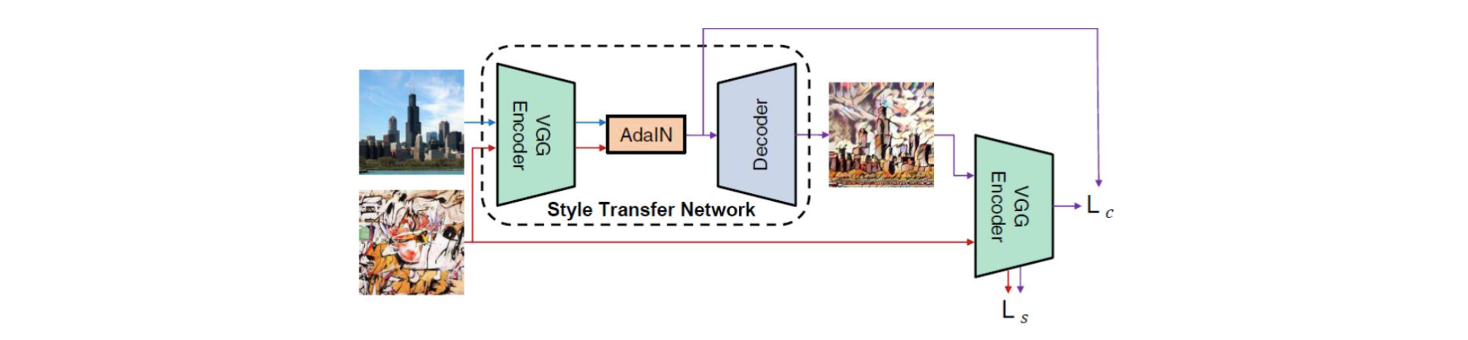요약하자면 아이디어는 정말 간단하다. Feature distribution을 reference image의 distribtuion에 따라갈 수 있도록 바꿔서 최종적으로 style을 바꾸겠다는 것이다. 위는 이 논문에서 제안한 style transfer의 전체적인 neural network의 구조를 그린 것이다. 이는 optimization-based approach가 아니고 feed-forward neural network를 기반으로 동작하게 된다. 그래서 이 network는 VGG encoder-decoder 구조로 되어 있고, 그 사이에는 AdaIN layer가 추가 되어 있다.

VGG encoder는 먼저 source image를 가지고 feature map $x$를 구하게 된다. 또한 style reference image도 함께 사용해서 feature map $y$를 구하게 된다. 그리고 feature map $x$의 distribution을 feature map $y$의 distribtuion을 사용해서 $x'$으로 바꾸게 된다. 이후 $x'$을 decoder에 넣어서 style transferred result를 얻을 수 있다. 전체적으로 간단한 구조를 가지고 있으며 이 논문에서 추가적으로 퀄리티를 올리기 위해서 노력을 했지만, 이는 그리 중요한 부분은 아니다.