[그래프 기계학습] Design Space of Message-Passing Graph Neural Networks

JAEYOON SIM·2024년 3월 4일

Machine Learning for Graphs

목록 보기

5/27

Design Space of Message-Passing GNNs

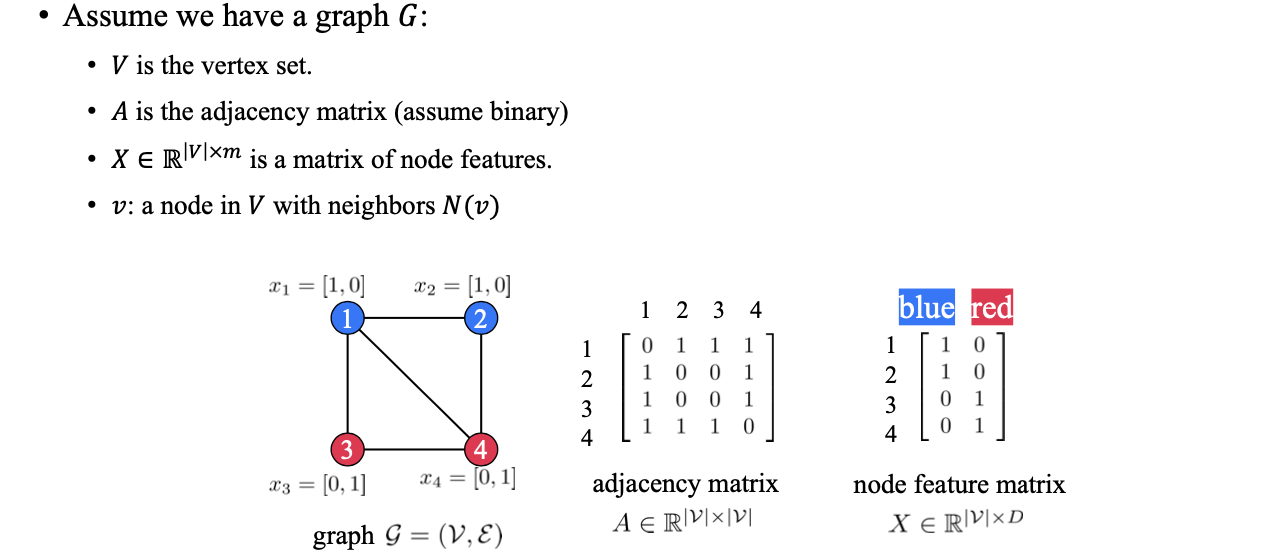Graph $G$ 가 있고, $V$ 는 vertex set, $A$ 는 adjacency matrix, $X$ 는 node feature를 표현하는 matrix라고 해보자. 그리고 node $V$ 에 대해서 이웃한 neighbor node들을 $N(v)$ 라고 해보자. 이제 우리는 주어진 graph의 구조를 파악할 수 있는 permutation-invariant하거나 permutation equivariant한 어떠한 graph neural network (GNN)을 만들고자 할 것이다.

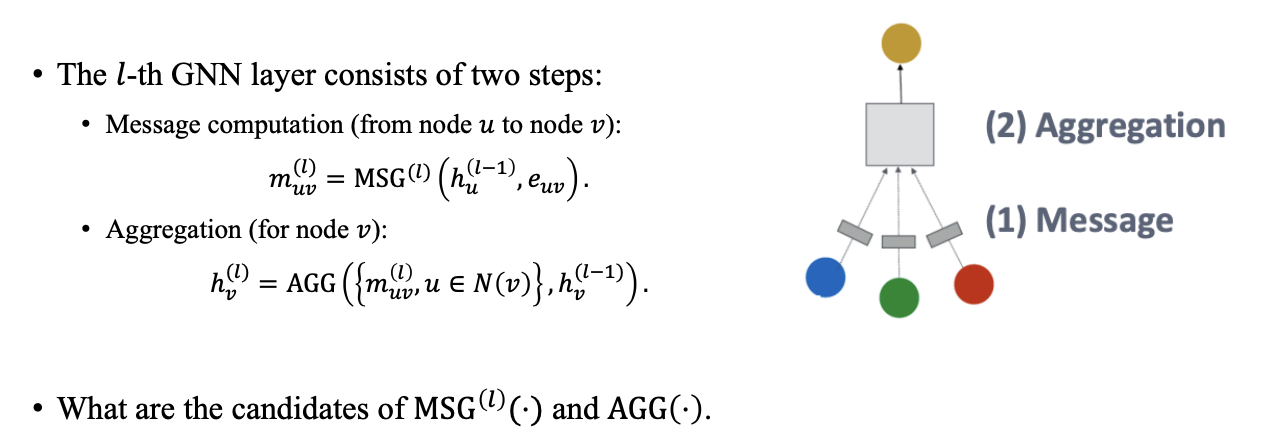우리는 GNN을 다양한 표현으로 나타낼 수 있고, 이번에는 최대한 간단하게 표현하면서 설명해보고자 할 것이다. GNN은 일반적으로 message computation과 update의 총 2-step으로 layer를 구성하게 된다. 일반적으로 layer를 통해서 node $u$ 로부터 node $v$ 로 어떠한 message를 전달하게 되고, 우리는 이러한 message를 $m_{uv}$ 라고 정의할 수있다. 어떠한 node $u$ 로부터 $v$ 까지 message를 보내고자 할 수 있고, 어떠한 node도 다른 node들로부터 message를 받을 수 있다. 그리고 message를 전달했으면 aggregation step에서는 node $v$ 가 이웃들로부터 받은 message를 모아서 자신을 update하게 된다. 즉, aggregation function $AGG$ 는 이웃들로부터 message를 모아주는 역할을 하는 operator가 된다. 결과적으로 우리는 GNN layer에 따라서 node별로 hidden feature를 update 할 수 있게 된다.

우리가 흔히 아는 GCN, GraphSage, MPNN 등과 같은 여러 GNN 모델은 message function과 aggregation function을 어떻게 구성하고 선택하는지에 따라서 모델이 구성되어져 있다. Message computation step을 우리는 feature들의 parameterized node-wise 혹은 edge-wise transformation으로 생각할 수도 있다. GNN layer를 거치면서 만들어지는 hidden feature는 각 node들로부터 message computation을 거친 결과로 볼 수 있고, 이들이 aggregation step에서 하나로 합쳐져서 최종적으로 message가 전달되는 식으로 각 node가 정보를 모을 수 있게 된다.

일반적으로 우리가 $u$ 에서 $v$ 로 message를 보내게 된다면 우리는 feature $h_u$ 들로 시작해서 각 node마다 feature간 matrix multiplication을 계산하고 non-linearity를 적용해서 이들을 최종적으로 aggregation을 해서 $h_v$ 를 만드는 것으로 이해할 수 있다. 이번에 살펴볼 내용들은 일종의 set function으로 불리는 여러 function들로부터 aggregation step을 우리가 어떻게 디자인할 수 있을지에 대해 집중되어 있다. Set function들은 또한 sum, max, attention 등과 같은 pooling function으로 부르기도 한다. 그리고 중요한 점은 이러한 set function은 permutation-invarint를 만족해야 하기에 output은 어떠한 input이 들어와도 결과가 변해서는 안된다. 이러한 부분은 실제로 GNN에서 정말 중요한 부분이다. 만약 논문에서 새로운 set function을 디자인 했다면, 이는 set data를 처리하는 새로운 GNN 구조를 디자인 했다는 것과 동일하게 볼 수 있다. 그리고 뒤에서 이야기하겠지만, 정말 유명한 set neural network 중 하나가 바로 transformer이다.

Prediction Heads for Different Tasks

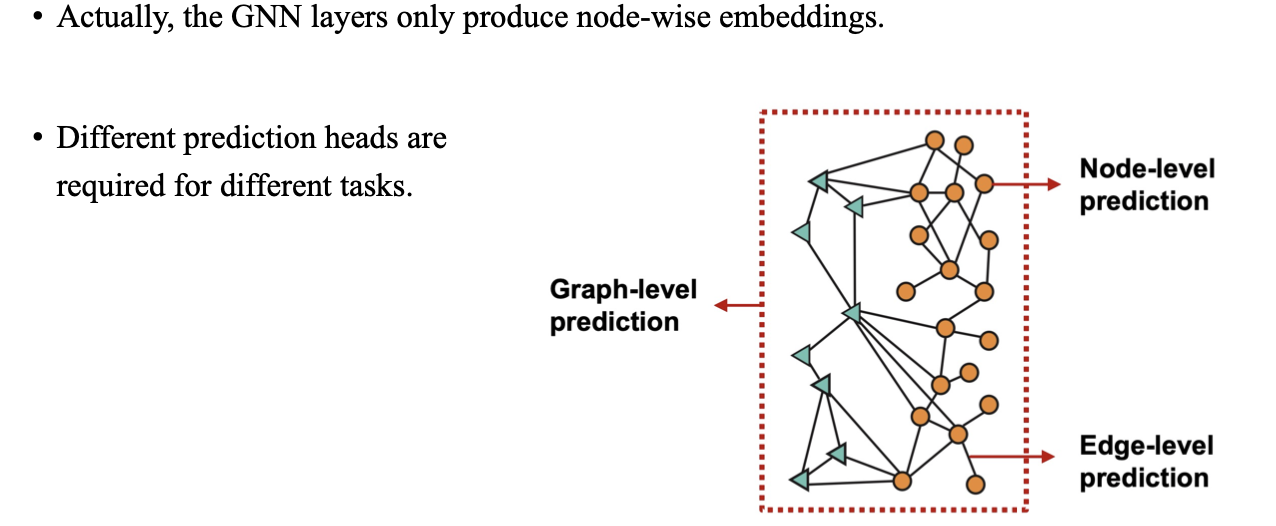지금부터는 node-wise hidden feature 혹은 node feature를 update하는 것에 대해서 이야기해보고자 한다. 만약 우리가 graph-level prediction을 한다고 해보자. 우리는 주어진 graph가 정상인지 아닌지, 혹은 이 graph가 무엇인지 예측해야 한다. 우리가 이러한 하나의 결과를 도출하기 위해서는 모든 vertex로부터의 정보를 aggregation하는 특정 head가 필요할 것이다. 아니면 때로는 우리가 각 node가 무엇인지 예측하는, 예를 들어 각 node의 색깔을 구분하는 것과 같은 node-level prediction을 하고자 할 때도 있을 것이다. 아니면 vertex pair가 연결되어 있는지, 혹은 두 vertex가 어떠한 관련이 있는지를 예측하는 edge-level prediction을 해야할 때도 있을 것이다.

결국 이렇게 원하는 결과를 도출하기 위해서는 hidden layer를 잘 update하는 것이 중요하다. 그리고 이렇게 update하여 얻은 마지막 hidden layer의 결과를 prediction head를 이용해서 어떻게 처리해서 원하는 방향으로의 결과를 도출할 수 있을지 알아보고자 한다. 물론 모두 다른 task이기 때문에 output space 자체가 다를 것이고, 이에 따라 서로 다른 prediction head를 요구하게 될 것이다.

Node-level prediction

우리는 node embedding을 이용해서 prediction 결과를 바로 만들기 때문에 node-level prediction에서 사용되는 head가 가장 기본적인 형태라고 생각할 수 있다. 이는 간단히 node-level embedding을 모아서 prediction을 하는 구조로, 여기에 MLP나 softmax를 적용해서 prediction을 할수도 있다. 즉, 우리는 그저 마지막 hidden layer에서 각 vertex의 embedding으로부터 node-level prediction을 수행할 수 있다.

사람들은 마지막 layer가 classifier로서의 역할에 대해서 중요한 부분에 대해서 알게되었다. 실제로 prediction head를 마지막 linear layer에서 MLP로 바꾸는 것이 성능 향상에 기여한 사실이 있었다. 실제로 GNN 구조가 특정 task에 맞게 optimization되기는 하지만, prediction head의 영향력이 실로 대단한 것임이 밝혀지곤 했었다.

Edge-level prediction

Edge-level prediction은 edge의 type이 무엇인지를 밝혀내는 task이다. 물론 edge의 type이 무엇인지를 예측하기만 한다면 쉬운 task일 것이다. 여기서 edge-level prediction이 어려워지는 부분은 바로 두 vertex 사이의 연경성을 예측해야하는 link prediction이라는 task 때문일 것이다. Input graph에 대해서 발견되지 않은 edge가 있을거라고 예측하는 문제는 실제로 어렵다. 위의 예시에서는 vetex D와 E 사이에 edge가 있을지 없을지를 맞춰야하는 것이다.

이를 위해서 일반적으로 접근하는 방식으로는 두 vertex에 대한 node embedding을 선택하고 여기에 prediction head를 구성해서 edge-level prediction을 수행하는 것이다. 실제로 이 방법 외에 다른 방법들도 존재한다. 중요한건 우리는 항상 prediction head가 permutation-invariant 하기를 원한다. 그래서 $h_v$ 와 $h_u$ 대신에 각각의 $v$ 와 $u$ 를 선택하더라도 prediction 결과는 그렇게 많이 변하지 않아야 한다. 이것은 또한 function에 대한 일종의 set value input이기 때문에 이러한 문제를 푸는 것은 꽤 non-trivial하다고 볼 수 있다.

Edge-level prediction에서 head를 구성하는 가장 유명한 방법으로는 concatenation을 한 다음에 linear mapping을 하는 것이다. 이는 node feature 쌍이 주어졌을 때 이들을 단순히 concat해서 하나의 vector로 만든 다음에 linear function을 적용시켜서 matrix multiplication과 같은 결과를 만드는 구조이다. 하지만 이러한 방식은 permutation-invariant 하지 않다. Concatentation을 하는 순서에 따라서 그 결과가 달라질 것이기 때문이다.

그러면 permutation invariance를 위해서 더하는 과정을 넣으면 어떻게 될까? 하지만 이러한 경우 대부분 prediction head의 expressive power를 상당히 잃는 결과를 초래하게 된다. 그래서 사람들은 hidden feature를 더하는 것이 아닌 prediction 결과들을 더하는 방법을 생각하기도 했다. 그러면 $u,v$ 순서로 넣는 것과 $v,u$ 순서로 넣는 것이 동일한 결과를 만들어 내어 permutation invariance를 만족하게 될 것이다. 이러한 방법은 input을 concatenation하고 MLP를 사용했을 때 매우 유용한 접근 중 하나일 것이다.

Edge-level prediction에서 또 다른 prediction head로 dot product를 사용할 수도 있다. Dot product는 두 벡터간 유사성을 비교할 수 있다. 만약 $K$ 차원의 prediction 결과를 만들고 싶다면, 즉 $K$ 차원의 classifier를 만들고자 한다면, 우선 $h_u$ 와 $h_v$ 의 유사성을 측정하고자 $h_u^T h_v$ 를 구하기 위해서 inner product kernel을 도입해볼 수 있을 것이다. 여기서 similarity의 weight는 이러한 kernel을 사용할 때 각각의 차원에서 다르기 때문에 $K$ 개의 classification 결과를 만들기 위해서 weight matrix가 $K$ 개가 필요할 것이다. 이러한 식으로 inner product를 이용해서 similarity를 구하는 방식도 하나의 예시가 될 수 있는 것이다.

Graph-level prediction

마지막으로 쉬운 task 중 하나인 graph-level prediction에 대해서 알아보자. 여기서는 모든 node embedding을 사용해서 하나의 graph-level permutation-invariant prediction을 만들어야 한다. 성능 향상을 위해서 aggregation function과 비슷하게 mean pooling, max pooling, sum pooling 등을 적용시킬 수 있다.

GNN Dataset Splitting

GNN을 학습시킨다고 했을 때 구조적으로 CNN과 달라서 학습할 때 주의해야하는 부분이 존재한다. 이번에는 이러한 내용을 중점적으로 다뤄보고자 한다. 지금까지는 CNN과 달랐던 부분으로 task에 따른 projection head를 어떻게 사용하는지에 대해서 알아보았다. 이는 CNN과 다르게 graph에서는 edge-level prediction과 같은 GNN을 사용했을 때만 풀 수 있는 문제들이 존재하기 때문이다. 이러한 prediction head로부터 GNN에 맞는 prediction을 만들고 evaluation metric 또한 만들 수도 있다.
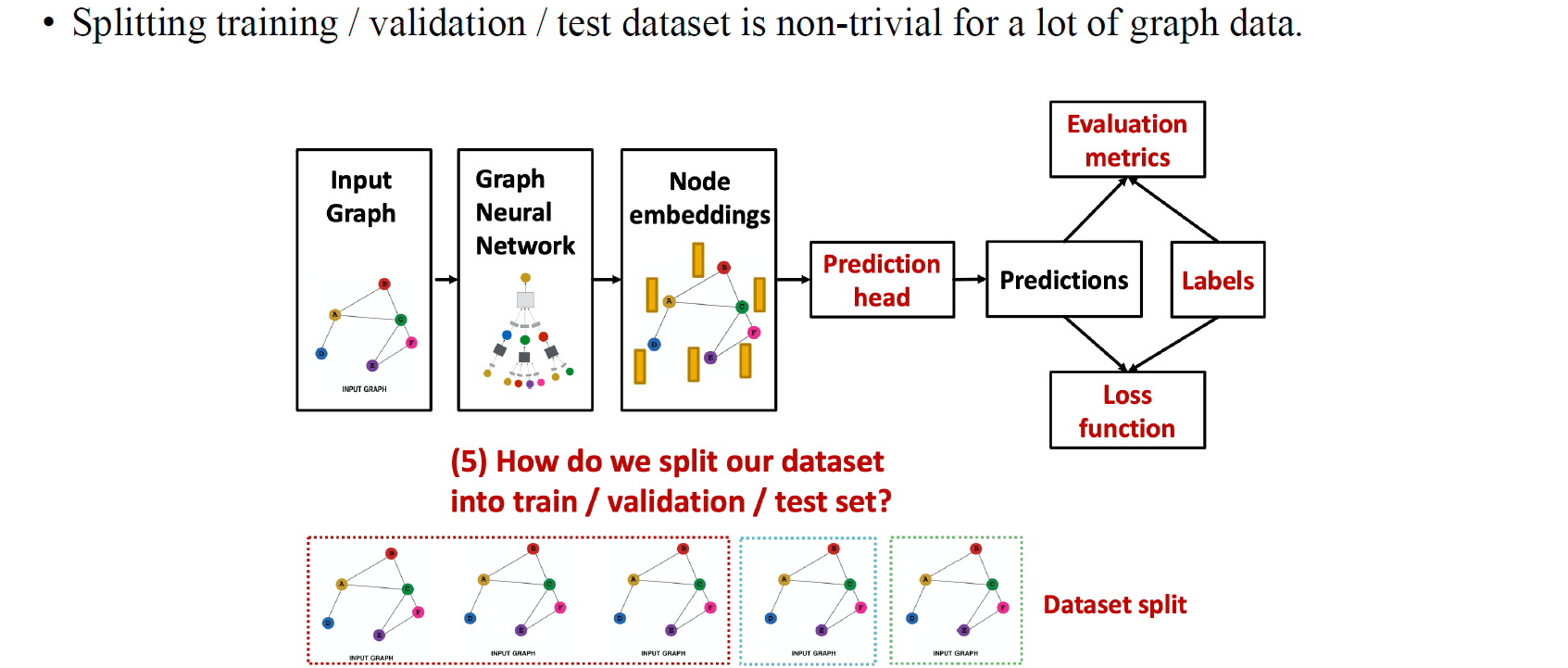GNN의 또 하나의 흥미로운 부분은 data를 split하는 것에 있다. Training, validation, testing으로 나뉘는 dataset 각각의 가정은 조금씩 다른 부분이 있다. 이번에는 이렇게 GNN을 학습시키고 평가할 때 사용되는 dataset을 어떻게 나눠야하는지에 대해서 알아보고자 한다.

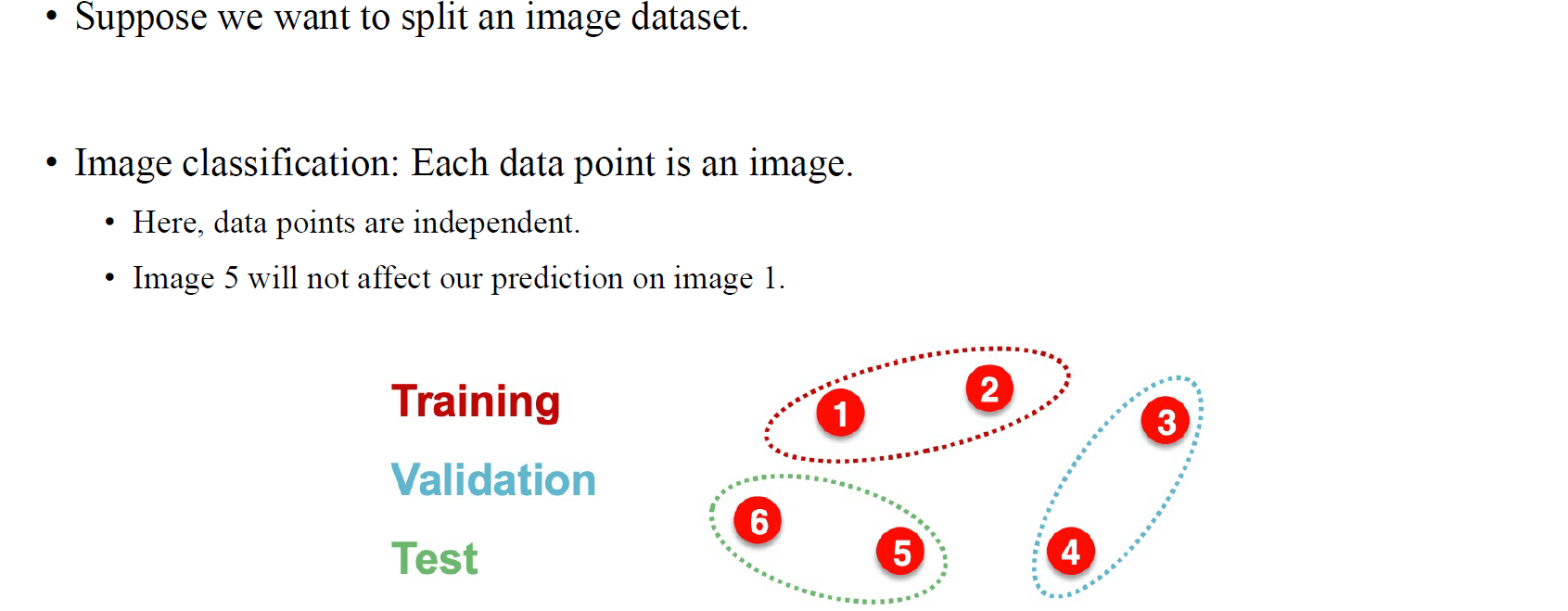먼저 이해하기 쉽도록 image dataset을 용도에 맞게 나누는 것은 상당히 쉽다. 위와 같이 총 6개의 data로 구성된 dataset이 있다고 해보자. 그저 training용으로 일부를 나누고, validation용으로 또 나눈 뒤 나머지를 testing data로 구성하면 끝이다. 물론 test에 사용되는 data가 training에 사용된 data에 영향을 줄 일은 없어야 한다.

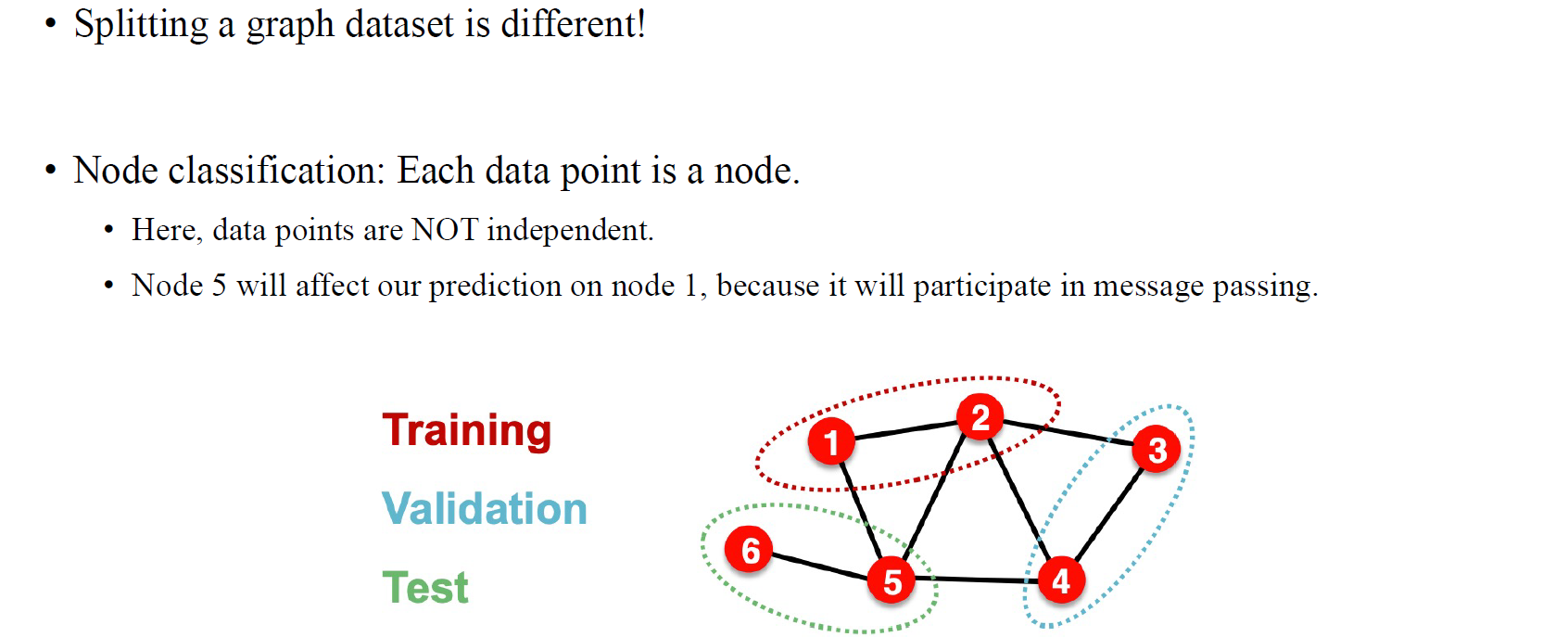하지만 graph dataset은 image dataset과 나누는 방법이 다소 다르다. 하나의 graph로 이루어진 dataset을 가정해보자. 그렇다면 하나의 graph에서 training, validation, test data를 어떻게 나눌 수 있을까? 문제는 그래프에서 임의로 vertex를 나눠서 test를 구성하게 되더라도 각각의 vertex가 independent하지 않기 때문에 이는 학습시에 model이 참고할 수 밖에 없다. 만약 test data를 나눠야 한다면 그래프에서 연결된 정보들을 날려보내는 수밖에 없을 것이다.

Transductive setting

그래서 GNN에서 data를 나누는 방식은 크게 두가지로 나눌 수가 있다. Transductive setting에서는 input graph에서 어떠한 정보도 날리지 않고 data를 임의로 나눈 뒤에 모델이 학습하게 만드는 것이다. 이때 training vertex들의 label정보를 참고해서 test vertex들의 label을 prediction할 수 있는 것이다. 물론 test vertex들의 정보는 학습시에 반영이 될 것이다. 이렇게 transductive setting에서는 전체 graph를 사용해서 training과 validation 시에 해당 vertex들의 label 정보는 참고하게 된다.

Inductive setting

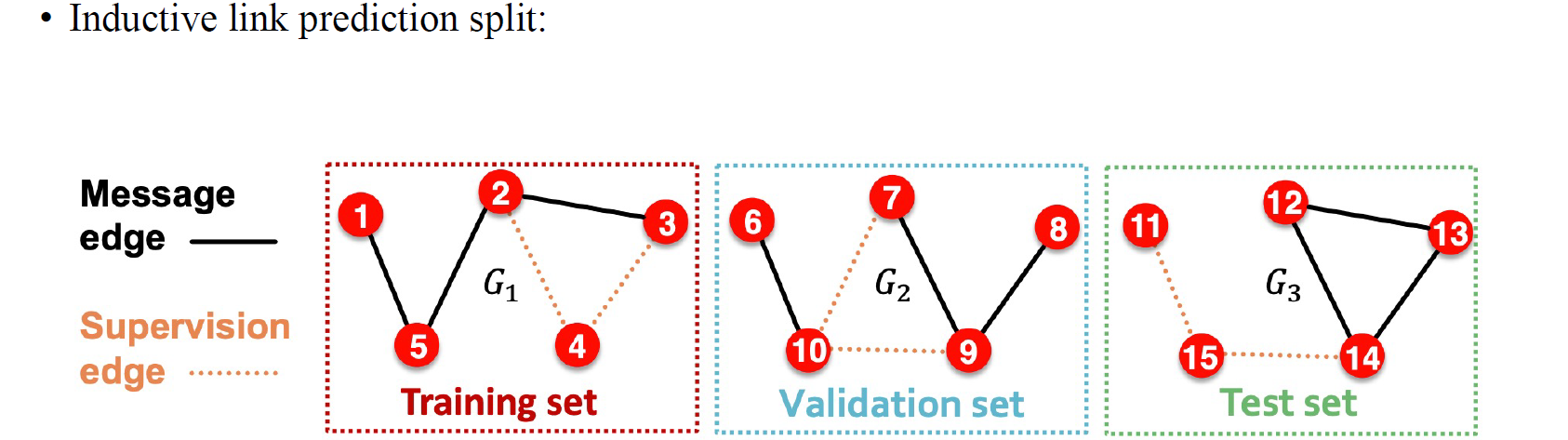
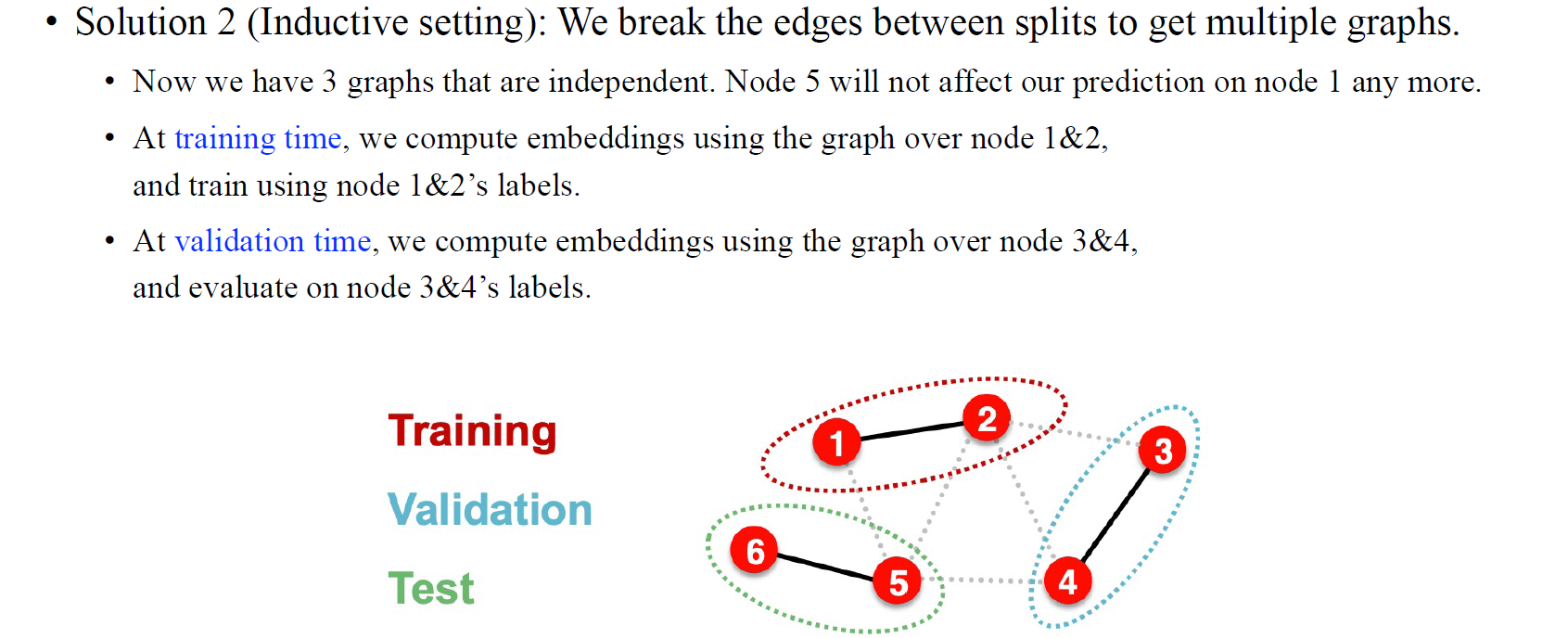두번째로 inductive setting에서는 연결된 edge들을 잘라 graph 하나를 여러 graph로 나누어 사용하게 된다. 위의 예시와 같이 training에는 1,2번 graph를 모델에게 보여주고 validation에는 3,4번 graph를 보여준 뒤 test에 5,6번 graph를 검증하는 식으로 진행된다.

Transductive / Inductive Settings

간단하게 기억하는 방법으로는 transductive setting에서는 학습하는 동안 동일한 graph에 해당하는 test data를 보지만, inductive setting에서는 test data에서 어느것도 보지 못한다. 보통 graph-level prediction에서는 우리가 하나의 prediction을 위해서 전체 graph를 보기 때문에 이는 inductive setting으로 볼 수 있다. Node-wise prediction에서는 대부분의 경우에는 transductive setting에 해당한다.

좀 더 구체적으로 transductive setting에서 모델을 학습시키는 경우에 각각의 vertex에 대해서 loss function을 디자인할 수 있고, test vertex에 대해서는 loss를 계산하지 않게 된다. 오로지 label이 무엇인지 알고 있는 vertex에 대해서만 loss를 구하게 된다.

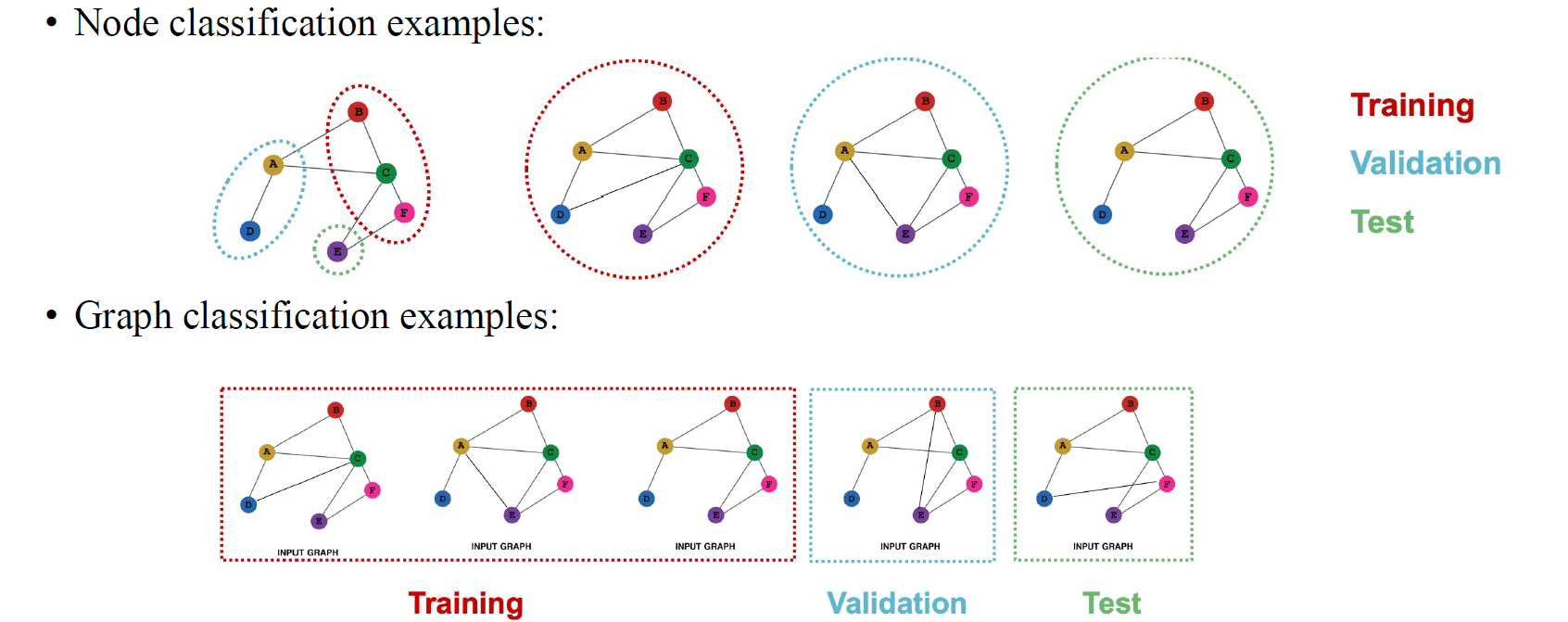정리해보면 node-level classification에서는 transductive setting과 inductive setting을 모두 수행할 수 있으며, graph classification에서는 일반적으로 inductive setting으로 좀 더 쉬운 문제를 풀게된다.

Link prediction

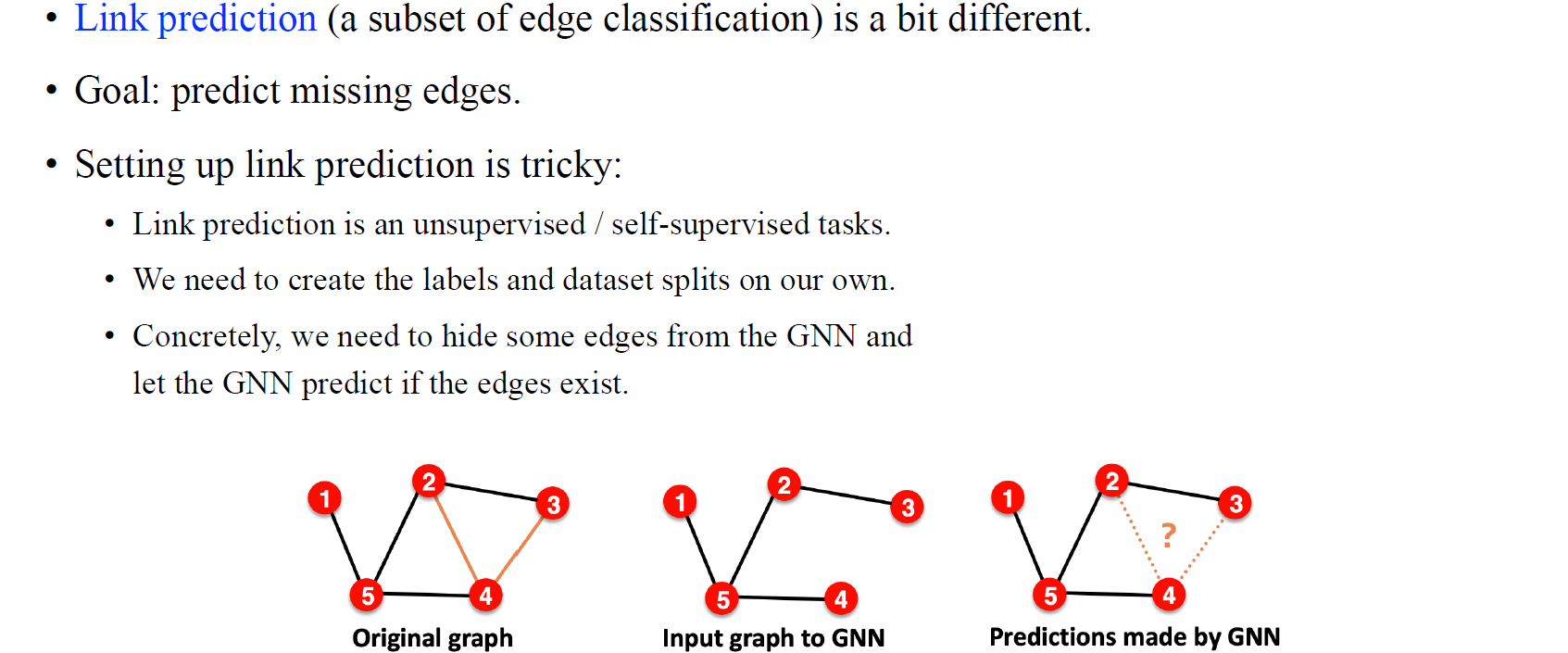또 다시 어려운 문제라고 하면 edge-level prediction이고, 이중에서도 link prediction이 조금 어려운 경우에 해당한다. 우리의 목적은 missing edge를 예측하는 것이고, 이를 위해서 특정 social network가 있다고 가정해보자. Social network에서는 두 사람 사이에 hidden link가 있는지 없는지를 예측해야만 한다. Link prediction에서 가정하고 있는건 해당 자리에서의 link를 input graph에서는 모른다는 것이다. 기본적으로 두 사람 사이에 link가 없다고 가정하지만, link prediction 문제에서는 두 사람 사이에 link가 알려지지 않았다는 가정이 있다. 그래서 link prediction 문제를 풀기 위한 세팅은 다소 까다로울 수 있다.

대부분의 node-level prediction에서는 input과 output을 쌍으로 가지게 된다. 하지만 link prediction의 경우에는 training dataset으로 우선은 전체 graph를 가지게 된다. 그리고 label과 neighbor들을 scratch로 지우게 된다. 모든 label을 지운다는 것이 link prediction에서 의미하는 바는 graph 구조를 지운다는 것이고, 결국 지워진 상태에서 missing link를 예측해야하는 것이다. 여기서 우리는 label을 link로 사용해서 prediction해야한다. 만약 우리가 100%의 link 혹은 label을 가지고 있다면, 여기서 90%의 link를 input으로 사용해서 10%의 missing link를 예측하도록 모델을 학습시키게 된다.

우리는 이러한 상황이기 때문에 link prediction을 unsupervised 혹은 self-supervised task로 볼 수 있다. 왜냐하면 원래의 전체 graph에서 시작해서 input graph를 만들기 위해 link를 지워주고 GNN에 이를 학습시켜 missing link를 예측하도록 만들기 때문이다. 이렇게 link prediction은 node-level prediction과 graph-level prediction보다 어려울 수 있지만, 이는 실제로 현실 상황을 더 반영한 문제로 보고있다.

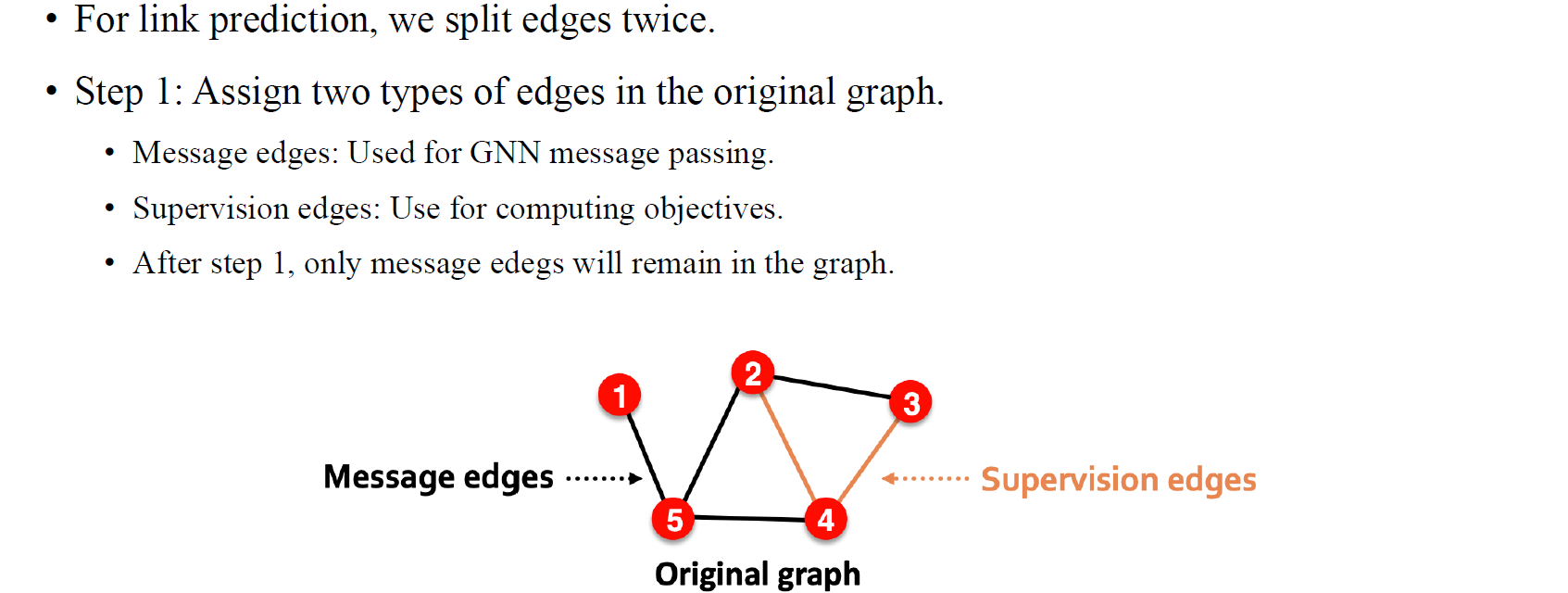좀 더 구체적으로 살펴보면 가장 먼저 해야할 일은 원래의 graph에서 모든 edge에 2종류의 type을 할당해주는 것이다. 정확한 이름을 할당하기는 어렵지만, message edge(input edge)와 supervision edge(output edge)로 나눈다고 생각해주면 된다. Message edge는 GNN의 message passing에 사용이 되고 supervision edge는 예측을 통해서 맞춰야하는 edge이다. 일반적으로 message edge의 비중이 supervision edge보다 더 크다.

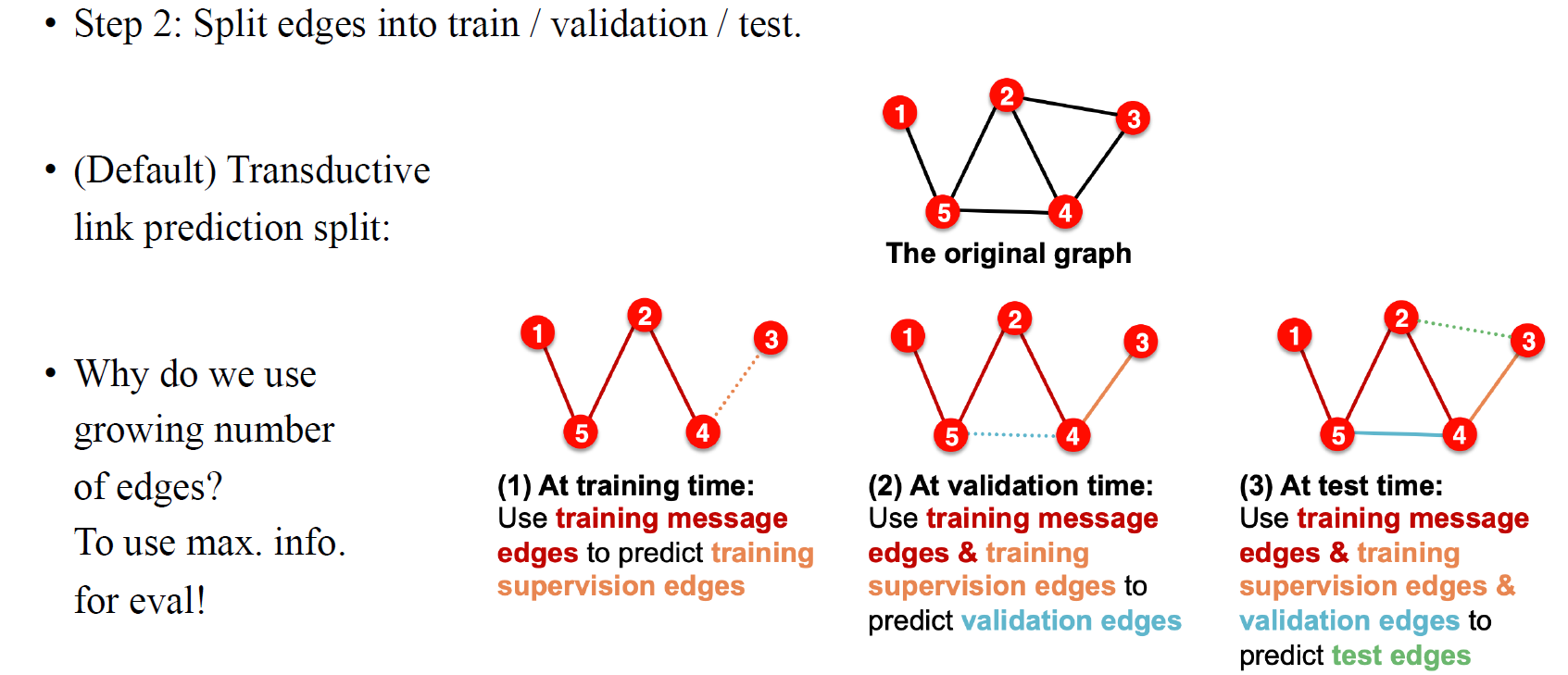그리고 이렇게 하는 것은 전체 graph를 training / validation / test dataset으로 분할할 때 더 이상할 수 있다. 전체 graph에 대해서 가장 먼저 하는 것은 test edge를 제외시키고 모델에 넣어 학습시키는 것이다. 그래서 학습시에는 message edge를 사용해서 학습을 시켜서 supervision edge를 일부 예측하도록 만든다. 그리고 검증시에는 training 동안 전혀 보지 않은 edge들을 예측하도록 한다. 이는 training시에 본 graph는 1%의 edge를 예측하기 위해서 98%의 edge로 구성되었다면, validation에서는 1%의 edge를 예측하기 위해서 99%의 edge로 구성된 graph를 사용하고, 마지막으로 test에서는 1%의 edge를 예측하기 위해서 100%의 edge로 구성된 graph를 사용하게 된다.