[그래프 기계학습] GNN, Attention, and Transformers

GNN and Attention

이번에는 GNN과 attention 사이에서 어떻게 개념이 연결될 수 있는지 알아보고자 한다. 지금까지 우리는 의도적으로 중요한 attention mechanism의 존재를 넘겨두고 있었다. 그만큼 중요한 개념이기에 이번에 자세하게 알아보고자 한다. GNN에서의 attention mechanism은 set data를 "pooling"하거나 "processing"하는 강력한 수단이다. 일반적으로 transformer는 sequencial data에서 동작하지만, 그 수식을 자세히 살펴보면 attention이라는 개념이 GNN에서 set data에 맞게 설계되었음을 알 수 있다. 그리고 attention mechansim이 실제로 GNN에서는 message passing step과 aggregation step에서 하는 것과 거의 동일하다고 볼 수 있다. 이러한 개념을 바탕으로 GNN에서는 graph attention network (GAT)와 graph transformer라는 중요한 모델들이 정의되고 만들어졌다. 실제로 graph transformer는 더욱 최신 연구라 흥미로운 부분이 많이 있다. 우리는 이들을 살펴보기 이전에 attention이 무엇인지에 대해서 알아볼 것이고, 이를 위해서 transformer 구조를 하나씩 뜯어볼 것이다.

Transformers Ingest Tokens

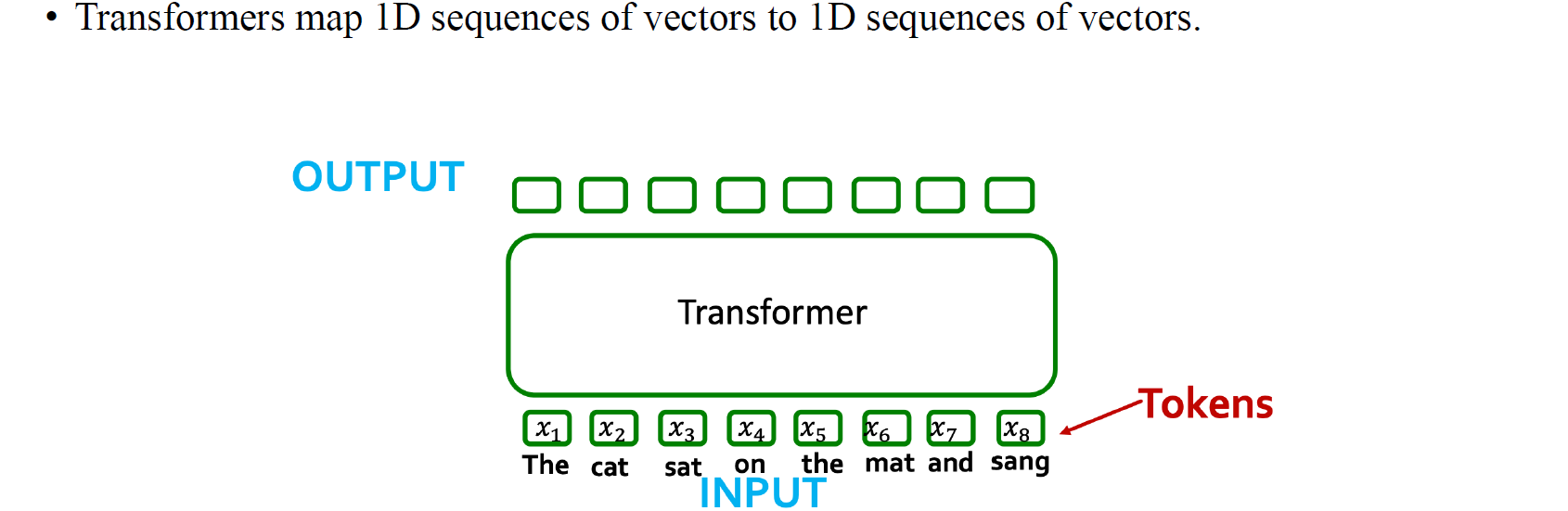NLP에서의 transformer는 token이라는 것을 수집하기 위해서 설계되었다. GNN에서의 token은 vertex들을 나타내거나 node feature들에 대응된다고 할 수 있다. Transformer는 일반적으로 token들 사이에 어떠한 순서 정보가 있다는 가정한다.

NLP에서는 token이 data의 "piece"를 설명하게 되고, 여기서 piece라고 함은 문장 속 단어들을 지칭할 수 있다. GNN에서는 이러한 token이 마찬가지로 data에서 특정 node feature를 가리킬 수 있는 것이다. Transformer는 보통 다음 token이 무엇인지를 예측하도록 output을 만든다. 위와 같이 The 다음에 cat이 오고 cat 다음에 set이 오는 식으로 다음에 어떠한 단어가 올지를 예측하게 된다. Attention을 이용해서 graph에서는 node feature를 예측할 수 있을 것이다.

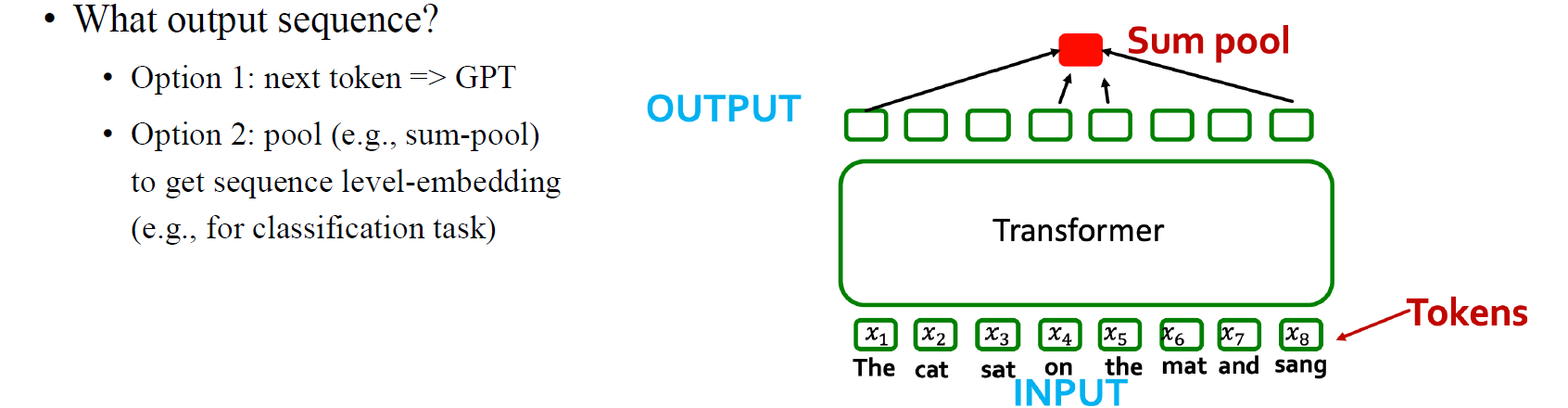또한 output으로 node-wise feature에 pooling function 등을 이용해서 graph-level prediction을 수행할 수도 있을 것이다.

Transformer Blueprint

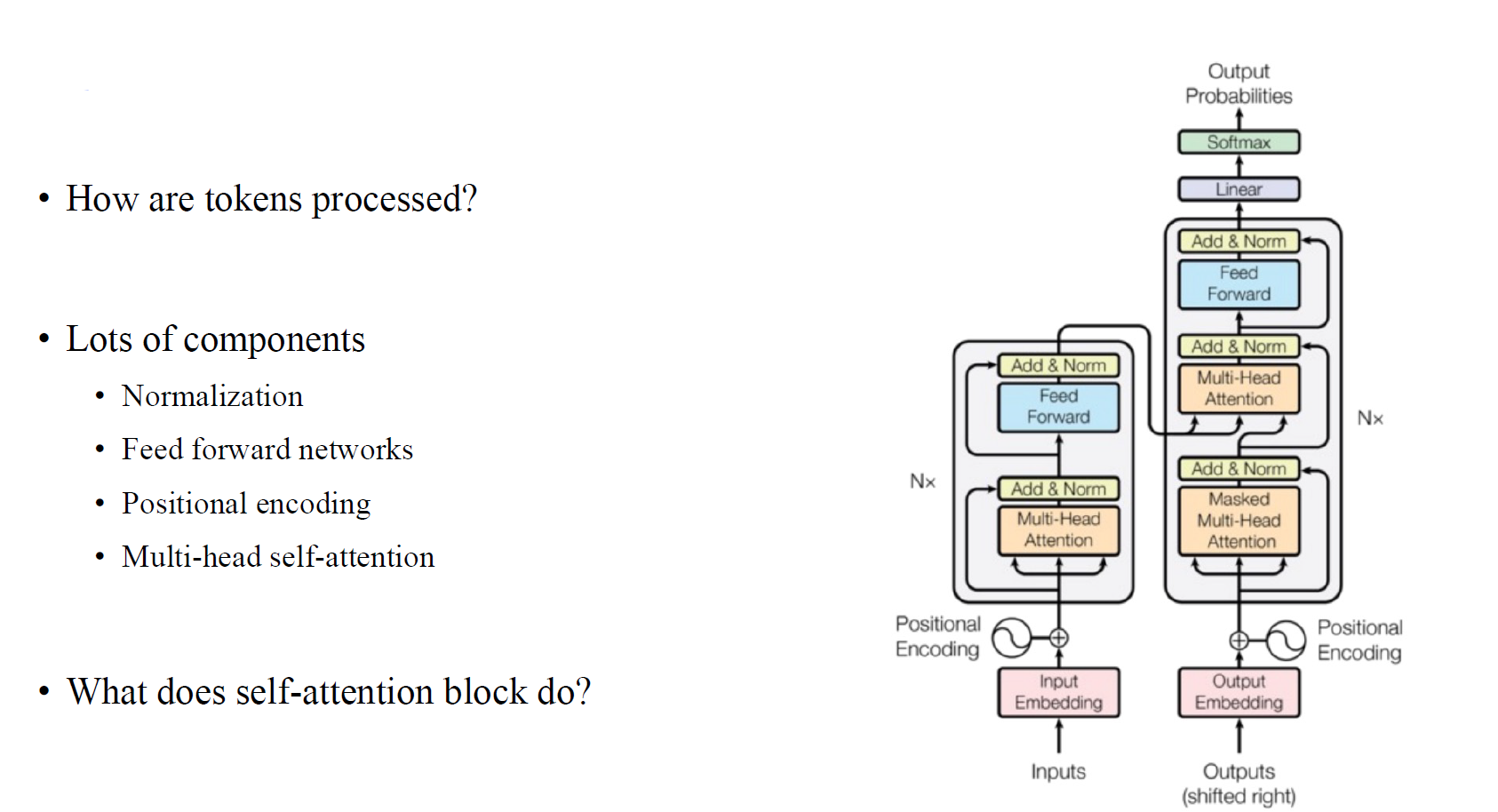Transformer 구조를 보면 굉장히 많은 component로 되어있는 것을 볼 수 있다. 특히 encoder와 decoder에 들어가기 전에 있는 positional encoding은 sequential data에 순서를 부여하여 모델에 추가 정보를 주는걸 볼 수 있다. 이렇게 많은 component들 중에서 이번에 중점적으로 볼 내용은 selt-attention mechanism이다.

Self-attention

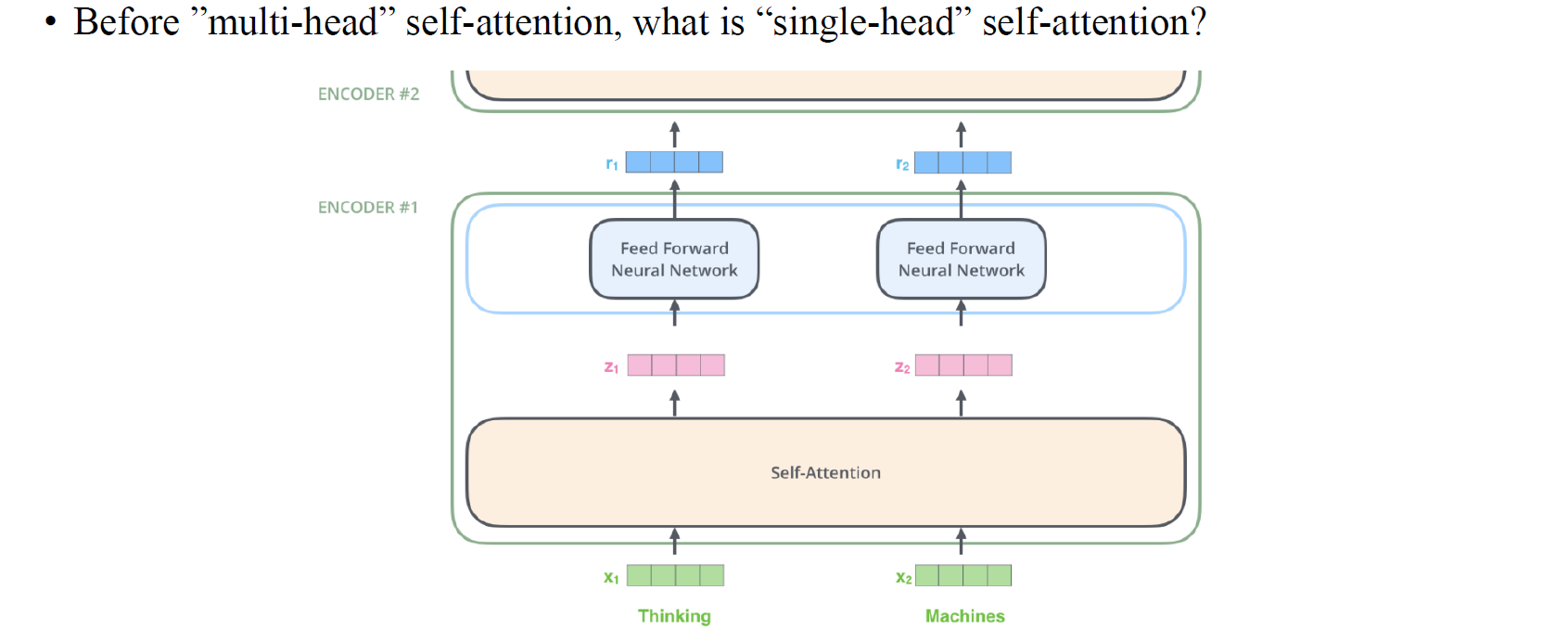사람들은 주로 multi-head self-attention을 사용하지만, 이는 single-head self-attention을 확장한 것으로 우리는 먼저 single-head self-attention이 무엇인지 보고자 한다. Self-attention의 아이디어는 원래의 node-wise feature들을 hidden feature들로 mapping하는데서 온다.

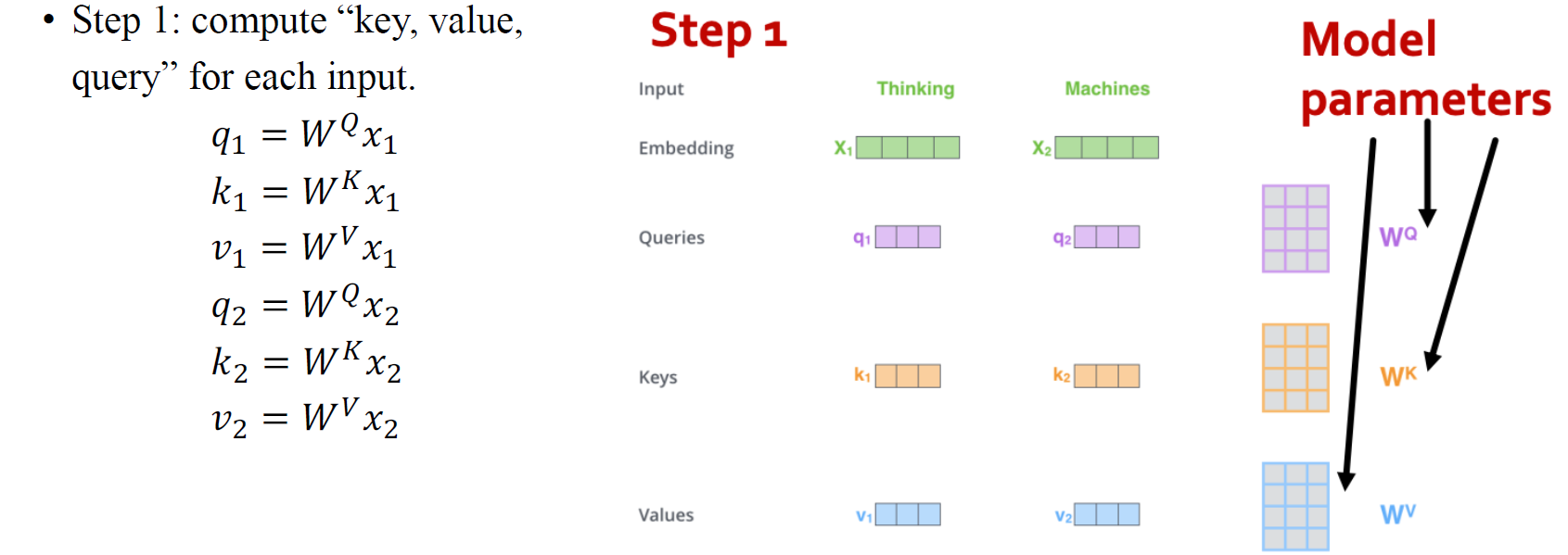이를 위해서 우리는 3개의 matrix가 필요하다. 크게 봤을 때 $W^v$를 input feature에 곱해줌으로써 node-wise feature transformation을 하고자하는 것이다. $W^v$ matrix가 중요한 이유는 서로 다른 node feature 사이의 interaction 보다는 각각의 node에 적용되기 때문이다. 우리는 node feature들이 서로 상호작용하기를 바라기 때문에 앞에 또 다른 matrix를 적용해서 곱해줄 필요가 있다. 즉, feature transformation을 하는 matrix도 필요하지만, 모든 node가 상호작용하기 위해서 서로 다른 node feature를 mixing하는 용도의 matrix도 필요하다는 것이다. 모든 transformer 관련 모델이 중점적으로 관심있어 하는 부분이 바로 mixing하는 matrix를 어떻게 디자인해서 node-wise feature들을 mixing할지이다.

결국 이를 위해서 $W^Q$와 $W^K$라는 2개의 matrix가 추가적으로 필요한 것이다. 예를 들어 위의 그림에서 각 node-wise feature $x_1$과 $x_2$에 대해서 3개의 matrix를 곱한 결과인 $q,k,v$를 feature마다 얻을 수 있게 된다. $v_1$은 node-wise transformation이라 생각하면 되고, $q_1$과 $k_1$은 node-wise feature를 섞기 위해 사용되는 일종의 재료라고 생각하면 된다.

우리는 이러한 과정들을 attention matrix를 만들어서 수행할 수 있다. 우리의 목적은 input feature들을 이용해서 hidden feature를 만드는 것이다. 이를 위해 먼저 $q,k,v$ 벡터를 만들고, $q,k$의 inner product를 계산할 것이다. 이러한 과정은 특정 query와 key 사이의 similarity score를 계산하는 것과 비슷하며, 이를 이용해서 다른 key들과 비교할 수 있다. 공학적인 목적으로 인하여 이렇게 계산한 결과들을 softmax를 이용해서 probability vector로 normalization해줄 것이다.

우리는 이렇게 얻은 matrix를 이용해서 각각의 $v$들의 가중치를 부여할 수 있게 된다. 이렇게 softmax vector를 이용해서 $v$들을 섞어서 다음 hidden 결과를 만들어낼 수 있다.

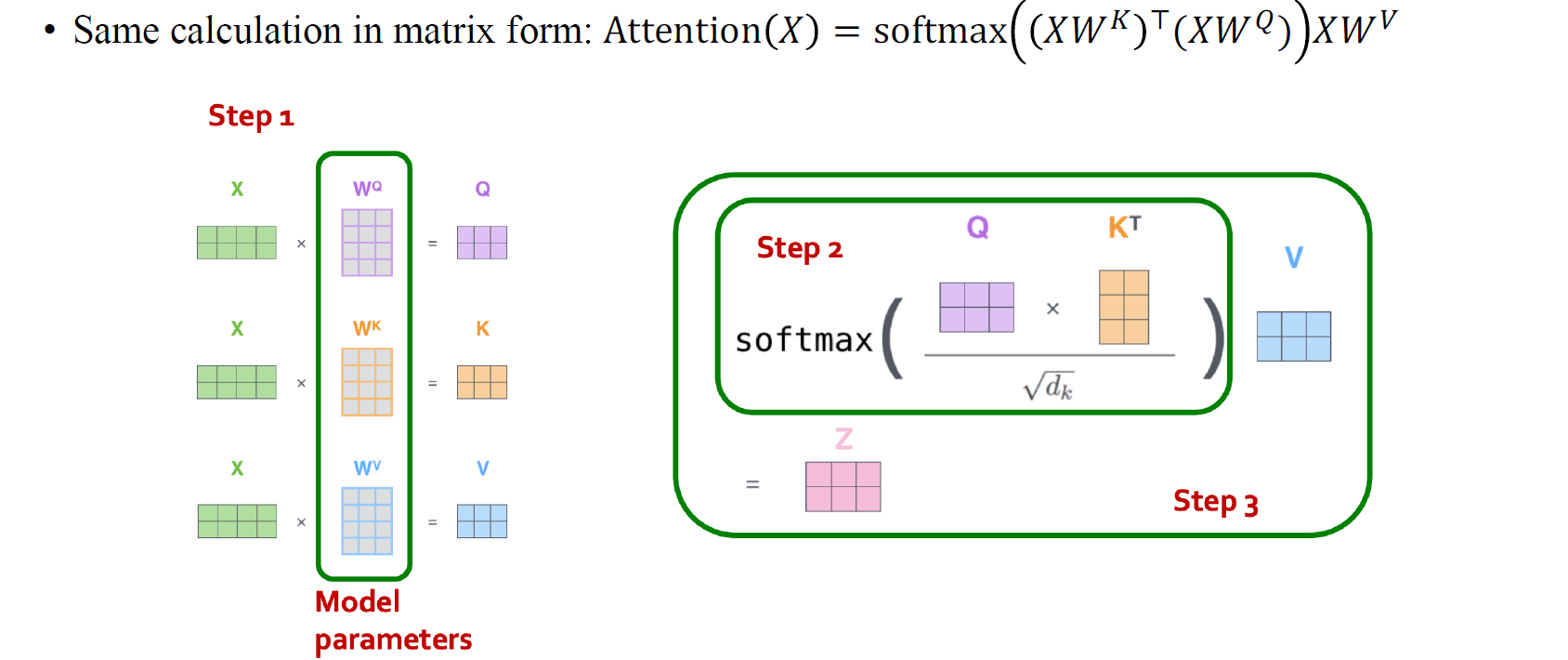위의 과정들이 조금 어렵게 다가왔다면 조금 더 쉽게 이해해보고자 한다. 우리의 목적은 결국 node feature들을 처리해서 hidden output을 만드는 것이다. 이를 위해서 $X$ 우측에 $W^v$를 곱해서 node-wise feature transformation을 할 수 있다. 추가적으로 좌측에 feature를 mixing해주는 matrix를 만들어서 곱해야 한다. 이때 $X$가 $v\times d$ matrix라고 한다면 좌측에 곱할 matrix는 $v \times v$ 여야 한다. 결국 우리는 좌측에 곱할 $v\times v$의 mixing matrix를 만들기 위해서 query와 key에 weight를 곱해서 서로 inner product를 취해주고, 이를 확률적으로 표현하기 위해서 softmax function을 취해준 것이었다. 이러한 결과가 결국 우리가 원하던 attention mechanism이다.

Multi-head Self-attention

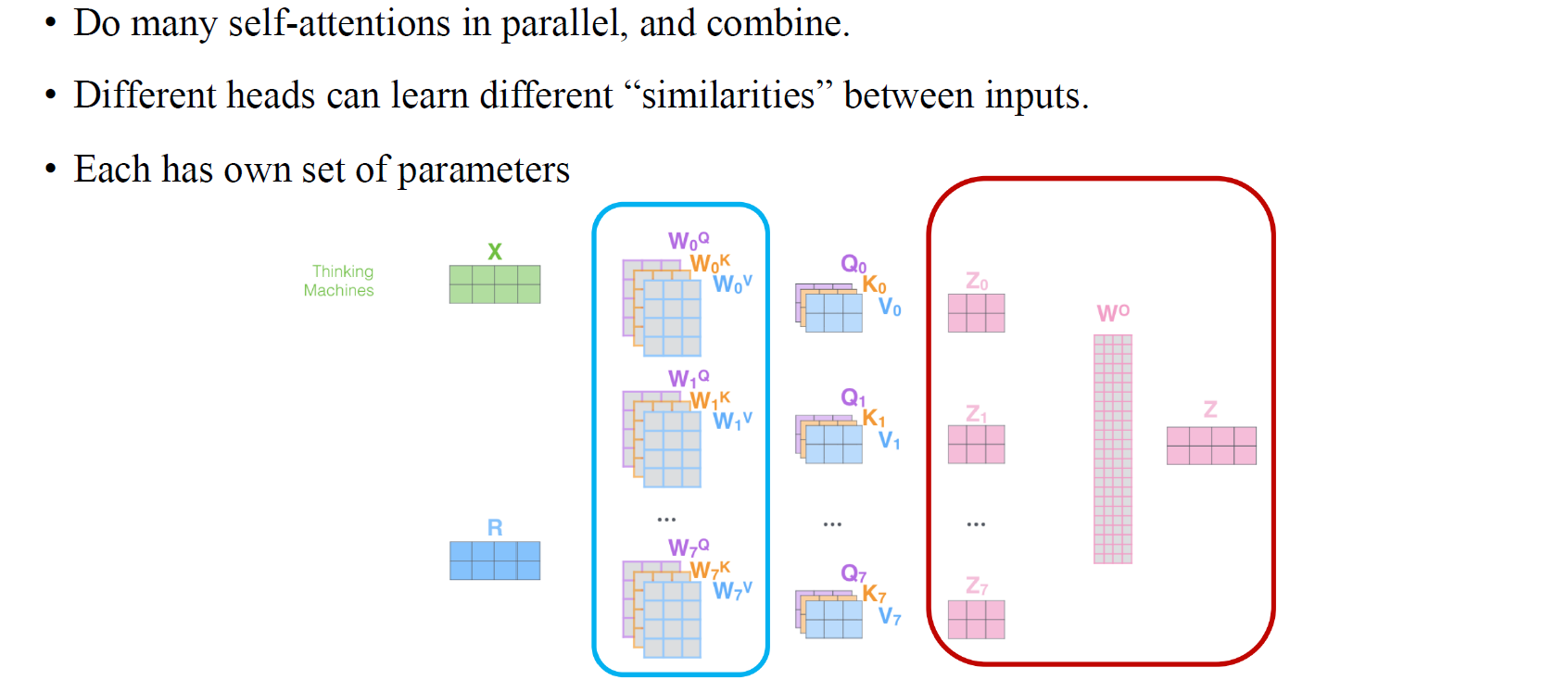Multi-head self-attention은 그저 weight matrix들을 다른 조합으로 표현한 것이고, 이는 위에서의 과정을 여러번했다고 생각하면 간단하다.

Comparing Transformers and GNN

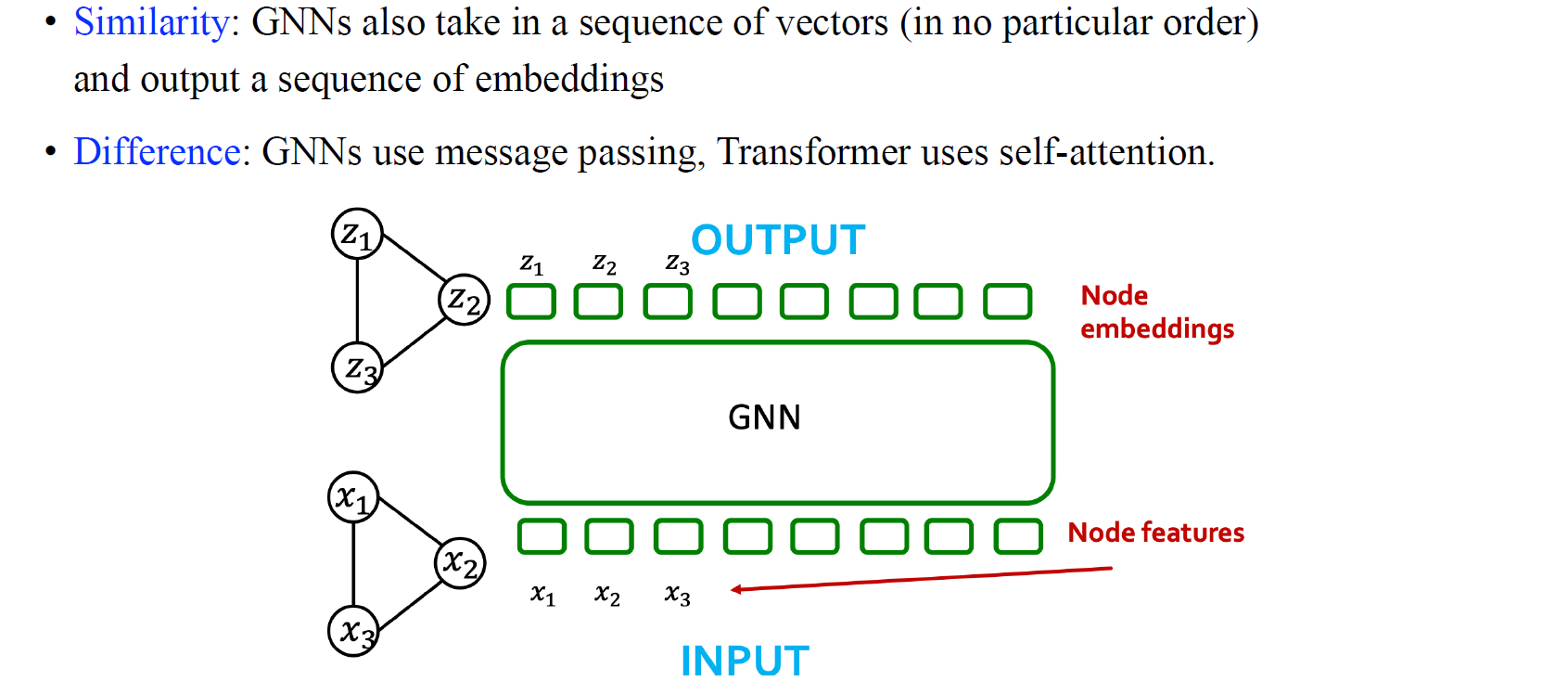결국 attention mechanism을 node-wise feature를 섞을 수 있는 mixing matrix를 만드는 과정으로 볼 수 있다면, GNN 또한 vector의 sequence를 input으로 가지고 node-wise embedding을 output으로 가지는 것을 볼 수 있기에 transformer와의 비슷한 성질을 지니게 된다. 이 둘의 차이라고 한다면 전체 input을 embedding으로 만든다고 했을 때 GNN은 이웃들로 범위가 제한되는 반면에 attention은 존재하는 모든 node로부터 feature들을 mixing할 수 있다. 이는 GNN이 message-passing으로 feature를 모으지만 transformer는 지금까지 살펴보았던 self-attention으로 전체 node로부터 feature를 mixing하기 때문이다.

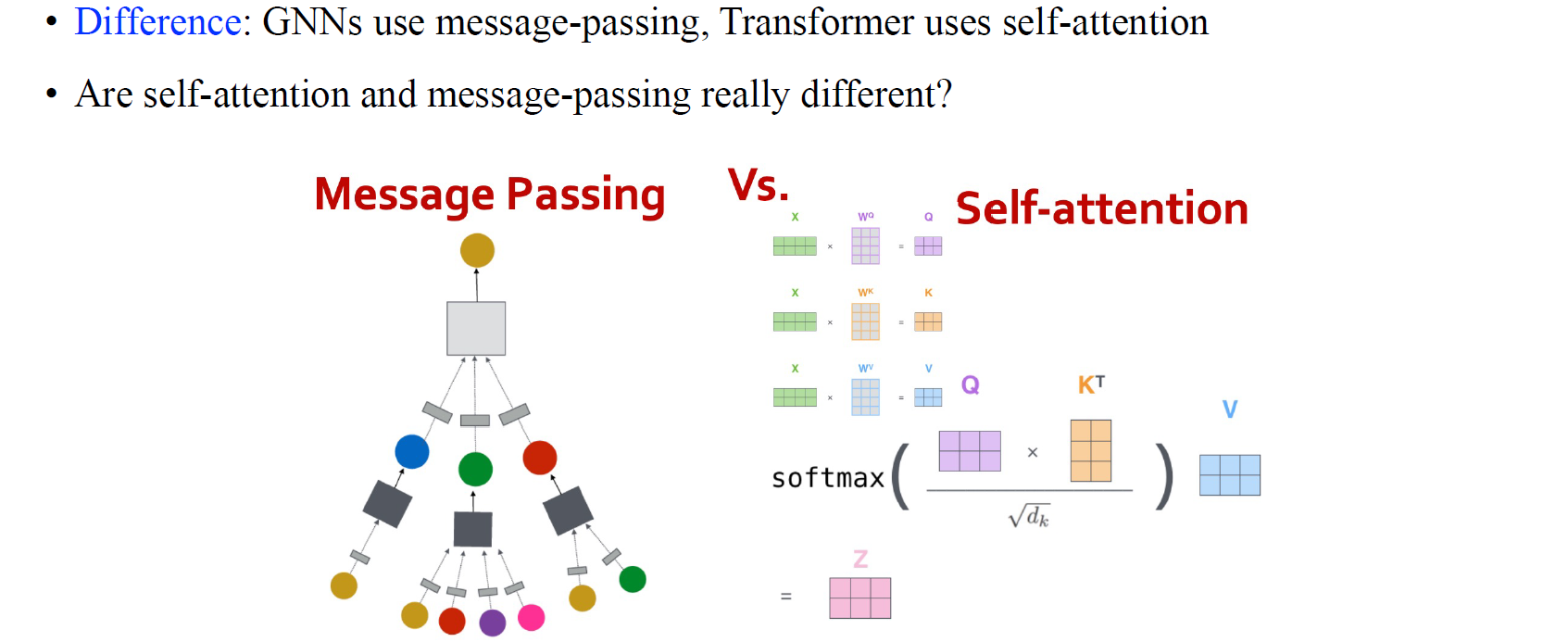일반적으로 GCN에서는 adjacency matrix를 이용해서 이웃들의 정보를 모으게 된다. 하지만 transformer도 동일한 과정을 하지만 단지 attention matrix를 이용하기 때문에 모든 node를 고려할 수 있는 것이다. 그리고 이렇게 만들어진 attention matrix는 mixing variable로써 각각의 node에 attention score를 할당하게 된다.

Self-Attention as Message Passing

좀 더 구체적으로 attention update의 식을 보면 $X$를 query, key, value로 사용하여 각각의 weight를 곱해준 뒤에 앞에 softmax를 취해주는걸 볼 수 있다. 그리고 여기서 우리는 softmax를 취한 결과로 얻어진 matrix를 attention matrix라고 부를 수 있는 것이다.

좀 더 자세하게 element-wise로 notation을 단순화할 수 있다. 우리가 특정 $x_v$를 $z_v$에 mapping한다고 했을 때 $v$에서의 결과는 존재하는 모든 node들에 대해서 summation되어 얻게 될 것이다.

그리고 이러한 summation은 aggregation step으로 볼 수 있다. $v_u$의 계산은 $XW$와 같은 결과일 것이고, 이는 message computation step으로 볼 수 있다. 결국 self-attention을 message passing의 하나의 방법으로 볼 수 있으며, 기존의 GCN에서와는 다르게 완전히 연결된 graph에 대한 message passing과 같은 효과로 해석할 수 있다. 즉, transformer는 graph가 완전히 연결되었다는 가정에서의 gcn과 같다고 볼 수 있는 것이다. 여기서 흥미로운 점으로는 전체 node에 대한 summation을 없애고 이웃 node들에 대해서만 summation을 고려하게 된다면 이는 graph attention network가 될 것이다.