[그래프 기계학습] Graph Attention Networks & Graph Transformers

Graph Attention Network

Graph attention network (GAT)를 이해하기 위해서 우리는 GCN의 message-passing update로부터 시작하고자 한다. 결론부터 이야기하자면 GCN에서의 aggregation step을 attention pooling으로 대체한다면 GAT가 될 수 있다.

GAT의 aggregation step에서 $\alpha$가 attention이라 불리는 가중치이고, summation은 오로지 이웃 node들에 대해서만 이루어진다. $\alpha_{uv}$는 일종의 softmax function으로, query $Q$와 key $K$들에 적용되는 가중치이다. 여기서 softmax function은 attention score를 normalization하여 각각의 이웃들에 대한 일종의 확률 벡터로 만들어준다. 예를 들어 두 노드에 대해서 적용한다고 하면 0.5 / 0.5와 같이 확률로 해당 score를 표현하게 만드는 것이다. 만약 우리가 graph를 fully connected network로 되어있다고 가정한다면 GAT는 Graph Transformer가 될 것이다.

원래의 GAT 논문에서는 $e_{uv}$를 더 나은 parametrization 방법으로 강조하고 있다. 2개의 hidden feature를 concat해서 linear layer를 통과시켜서 softmax를 적용시키는 것을 attention layer를 normalization하는 것이라고 설명한다. 이렇게 concat하고 linear layer를 통해 구해진 $e_{uv}$는 matrix product를 사용하는 원래의 transformer과는 약간의 차이가 있지만, 그들은 실제로 이렇게 하는 방법이 더 나은 성능을 보였다고 설명했다.

Graph transformer는 matrix multiplication을 통해서 fully connected된 graph에서 모든 node간 attention score를 구할 수 있다. 하지만, GAT에서는 connection이 매우 sparse하기 때문에 각 edge에 대해서 attention score를 matrix multiplication 없이 구해야 한다. Dense한 가정이 있는 transformer와 sparse하게 adjacency matrix를 사용하는 GNN에서는 실제로 implementation에서는 차이가 있을 수 밖에 없다.

GAT를 사용하는데서 오는 이점이라고 한다면, 서로 다른 이웃한 node들로부터 다른 값이 오기 때문에 서로 다른 중요도를 $\alpha$라는 가중치로 특정할 수 있다는 것이다. 또 다른 이점은 GCN, Graphsage와 다르게 GAT를 구하는 과정에서 상대적으로 조금 느릴 수는 있지만, 그래도 operation의 complexity를 고려했을 때 효율적인 계산이 가능하다는 점이다.

Graph Transformers

GAT에 대해서 어느정도 알았다면, 이번에는 graph transformer에 대해서 알아보고자 한다.

New Design Landscape for Graph Transformers

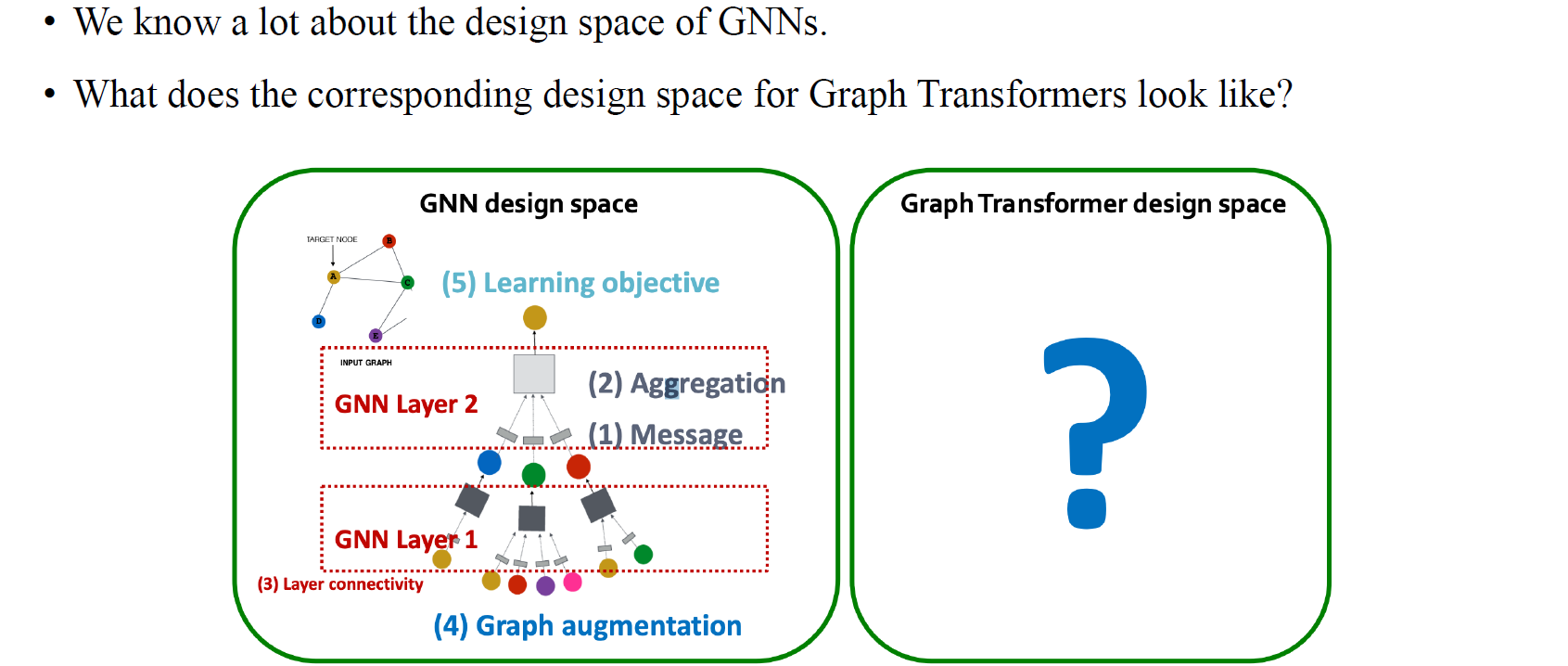Graph transformer는 기존의 transformer 구조와는 조금 다르지만 graph의 구조를 파악하기 위해서 살짝 변형되어 사용되었다. Graph transformer의 아이디어는 GNN을 생각해보았을 때 가장 먼저 이웃한 node를 파악하고 이 node들의 feature를 확인해야 한다. 그러면 이러한 이웃들로부터 정보들을 모아서 자신을 업데이트하는 구조로 message를 보내고 수정하게 된다. 하지만 graph transformer는 이러한 방법에서부터 다른 관점으로 접근하게 된다. 이웃들을 파악하는 것은 adjacency matrix를 파악하는 방법 중 하나일 뿐이며, graph transformer는 조금 다른 방법으로 이웃들을 파악하는데 초점을 두고 있다.

Processing Graphs with Transformers

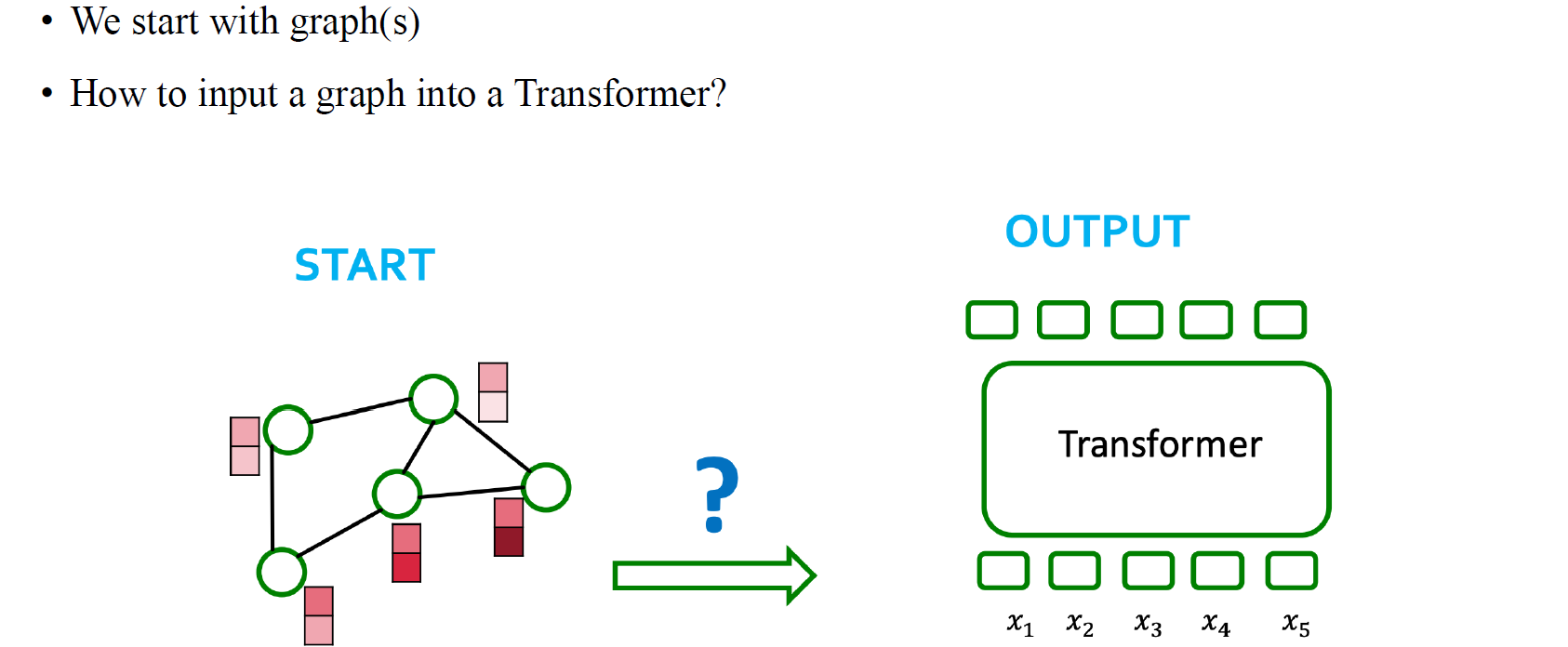그래서 기존의 message passing neural network의 관점이 아닌 transformer의 구조를 가지고 input으로 graph를 넣어 이를 파악하고자 모델을 설계하게 된다. Transformer는 graph를 설명할 수 있는 adjacency matrix로 부터 attention matrix를 만들어야 한다. 이렇게 만드는 방법이 graph transformer를 설계하는 간단한 방법 중 하나이다.

Components of a Transformer

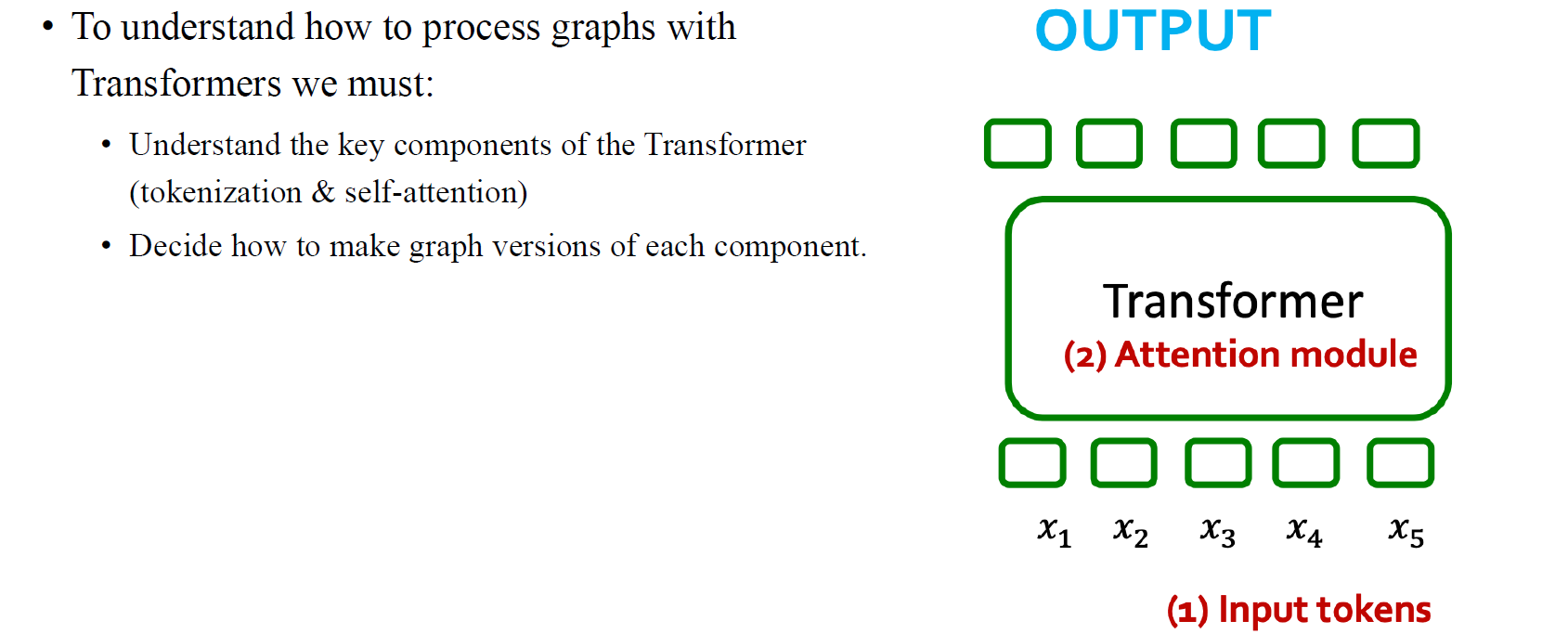만약 graph에 대한 transformer를 설계하고 싶다면, 가장 먼저 생각해야하는 것은 원래 transformer가 set value에 대해서 설계된 모델이라는 점이다. 그렇기 때문에 모든 node에 대해서 input의 position을 고려해야 한다. 물론 우리는 node feature로부터 시작하게 된다. Text data의 경우에는 원래라면 transformer 자체에서 단어들의 순서를 알 수가 없다. 하지만 이후에 설명하겠지만 transformer에서는 단어의 순서를 추가로 정보로 넣어주게 된다. 우리가 graph를 처리하고 파악하기 위해서 transformer는 graph를 input token으로 받아서 attention score를 구하고, 이를 바탕으로 원하는 output을 만들 것이다.

Final Key Piece: Token Ordering

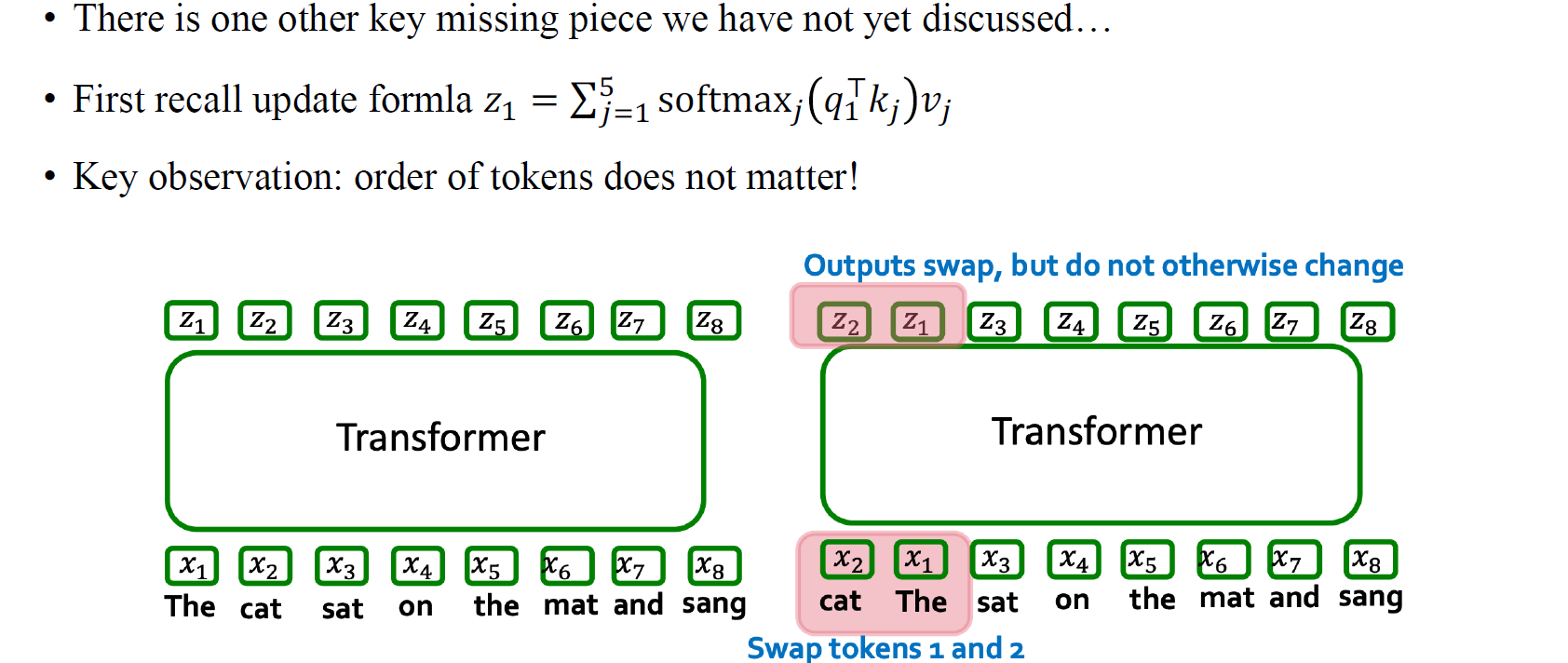기본적으로 token의 순서는 사실 transformer에서는 중요한 문제가 아니다. 만약 $x_1$과 $x_2$의 위치를 바꾸더라도 output $z_1$과 $z_2$가 permutation equivariance를 만족하기 때문에 마찬가지로 위치가 바뀌게 될 것이다. 그 이유는 우리는 aggregation step에서 permutation equivariant 혹은 invariant를 미리 node feature에 정의했기 때문이다. 이러한 성질을 transformer 구조는 그대로 따라갈 수 있다. token의 순서에 맞게 output의 순서가 달라지게 될 것이다.

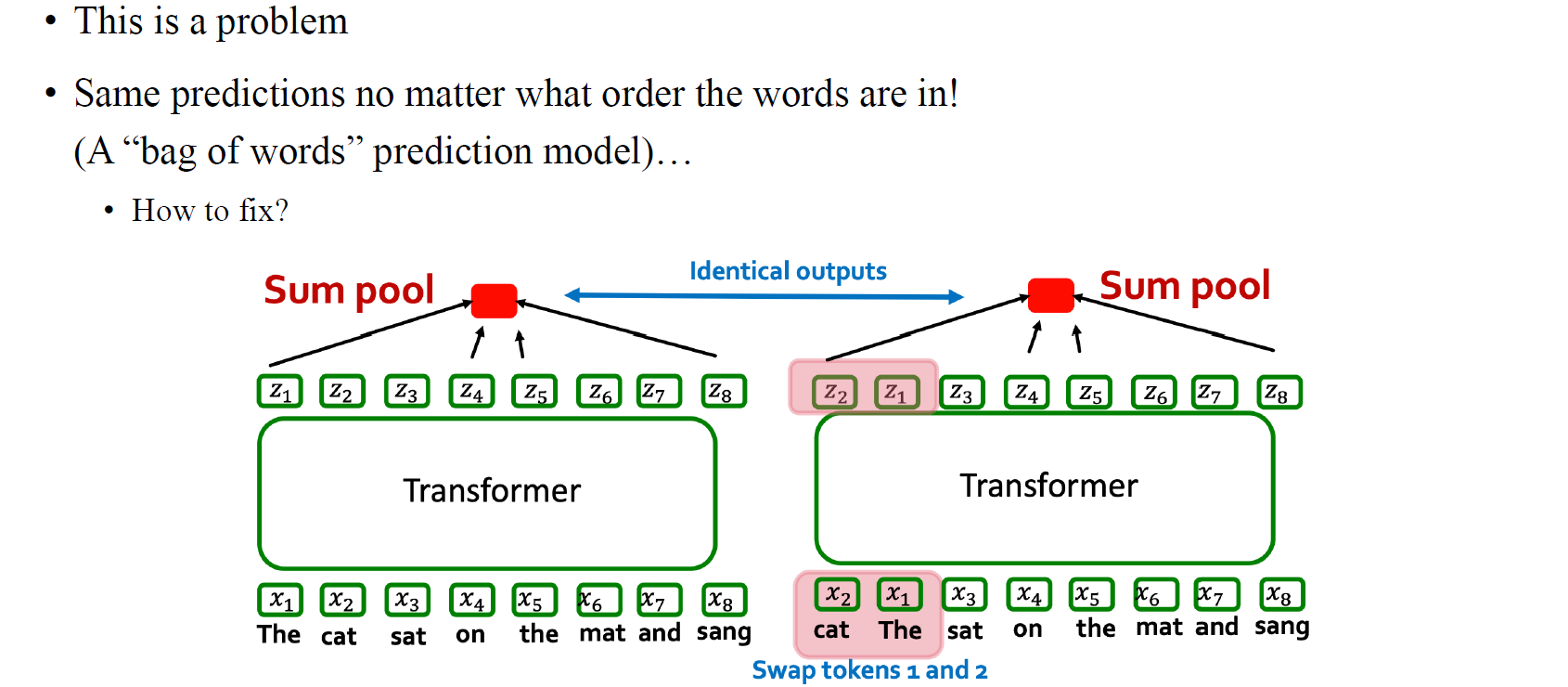이렇게 input의 위치에 따라 output의 순서가 달라지는 것은 transformer에서 중요한 성질이다. 하지만 단순히 input으로 text data나 node feature를 넣어주게 되면 넣어준 순서를 기반으로 이후에 정보를 모아주지만, 이 과정에서 문제가 생긴다. 순서가 중요하여 순서를 바꿔줌에 따라 바뀐 결과가 모아지게 되는데, 진짜 문제는 마지막에 수합하는 과정에서 sum pooling과 같은 연산을 하게 되면 결국 같은 output으로 결정이 될 것이다.

Positional Encoding

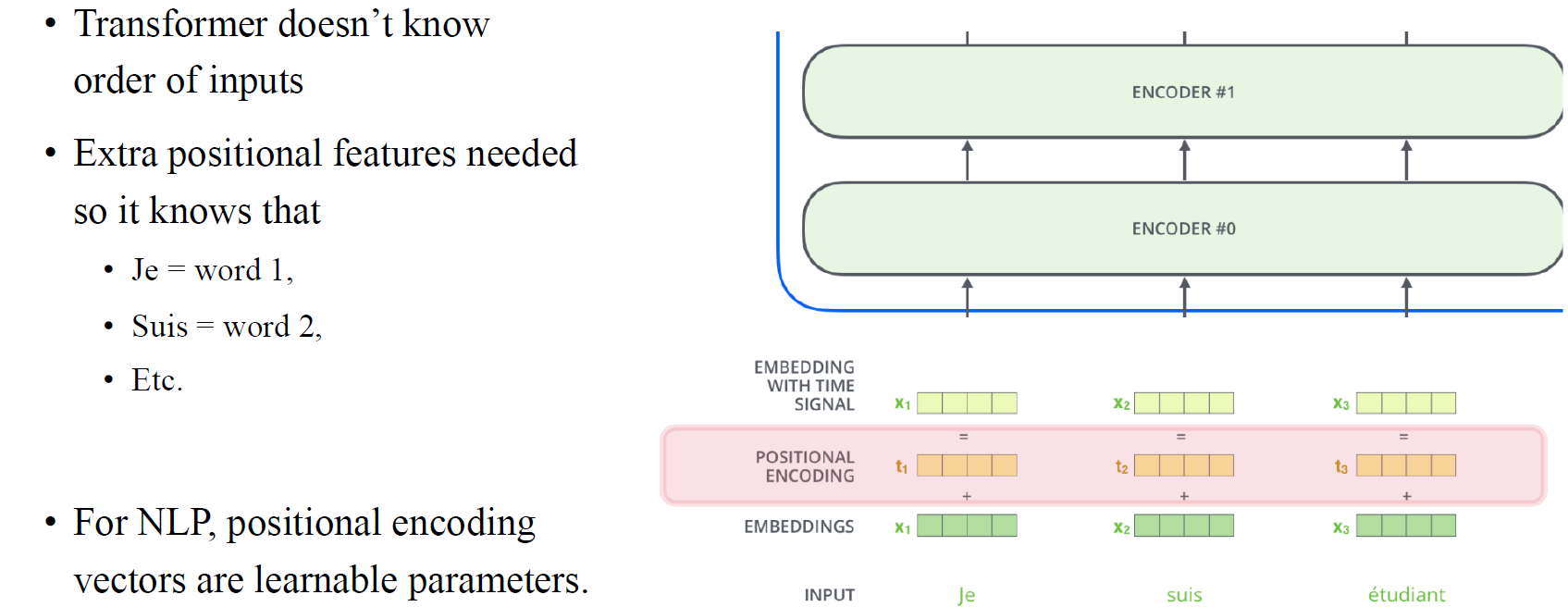그래서 사람들이 text data에서 해왔던 것은 input에 positional encoding을 추가로 설정해주는 것이었다. Graph에서는 추가로 node마다 feature가 생긴다고 생각하면 된다. Positional encoding은 결국 text data에서 중요한 문장에서의 순서를 각 단어마다 부여하는 것이고, 이렇게 추가된 정보를 기반으로 transformer는 input의 순서를 기억하게 될 것이다.

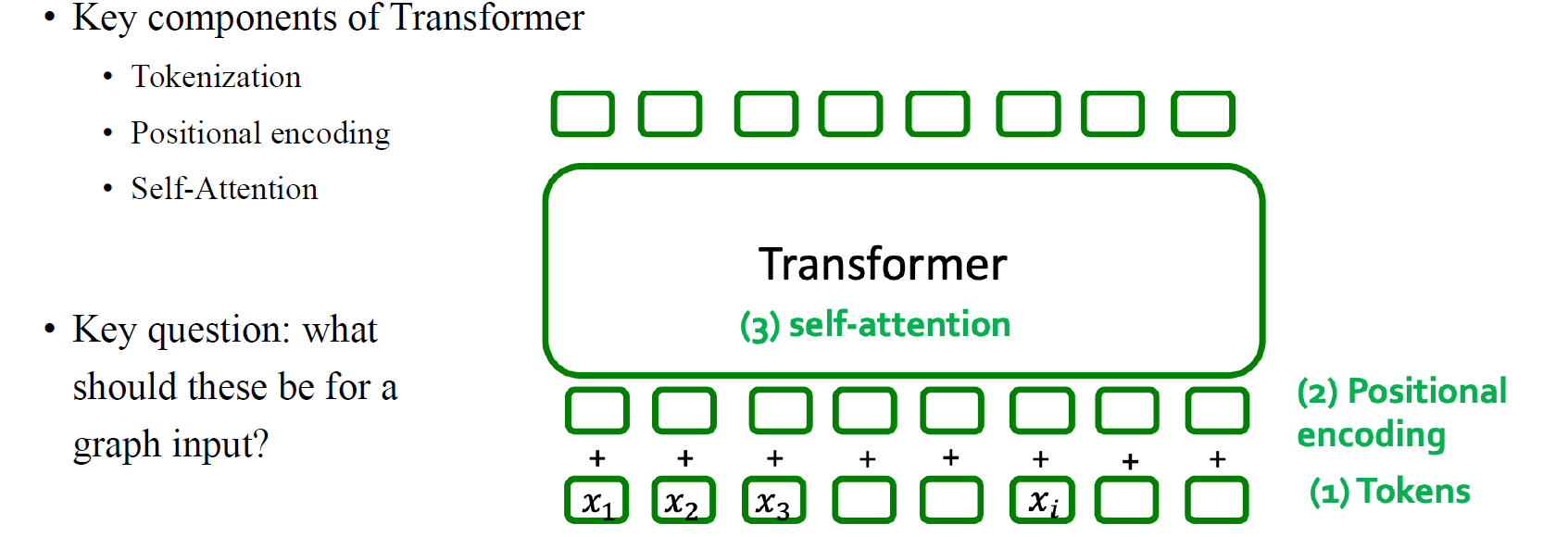그래서 결국 transformer를 설계할 때는 단순히 input feature를 모델에 넣어주는 것이 아니라 positional encoding을 이용해서 위치 정보를 추가해서 넣어줘야 한다. 이렇게 input의 tokenization을 시작으로 positional encoding을 거쳐 attention score를 구하게 되는 과정을 text data에서는 sequence로 자연스럽게 연결되는데, 그렇다면 graph에서는 정확히 어떻게 수행이 되는 것인지 알아보고자 한다.

Processing Graphs with Transformers (con't)

Graph data를 transformer가 처리하는 방식은 NLP와 다르지 않다. Graph transformer는 각 node feature를 각각의 token으로 하여 input으로 사용하면서 각각에 positional encoding을 추가해주게 된다. 이들을 이용해서 transformer는 self-attention을 통해서 attention score를 node별로 구할 수 있게 된다. 이러한 기본적인 구조는 다양하게 변형되어질 수는 있다.

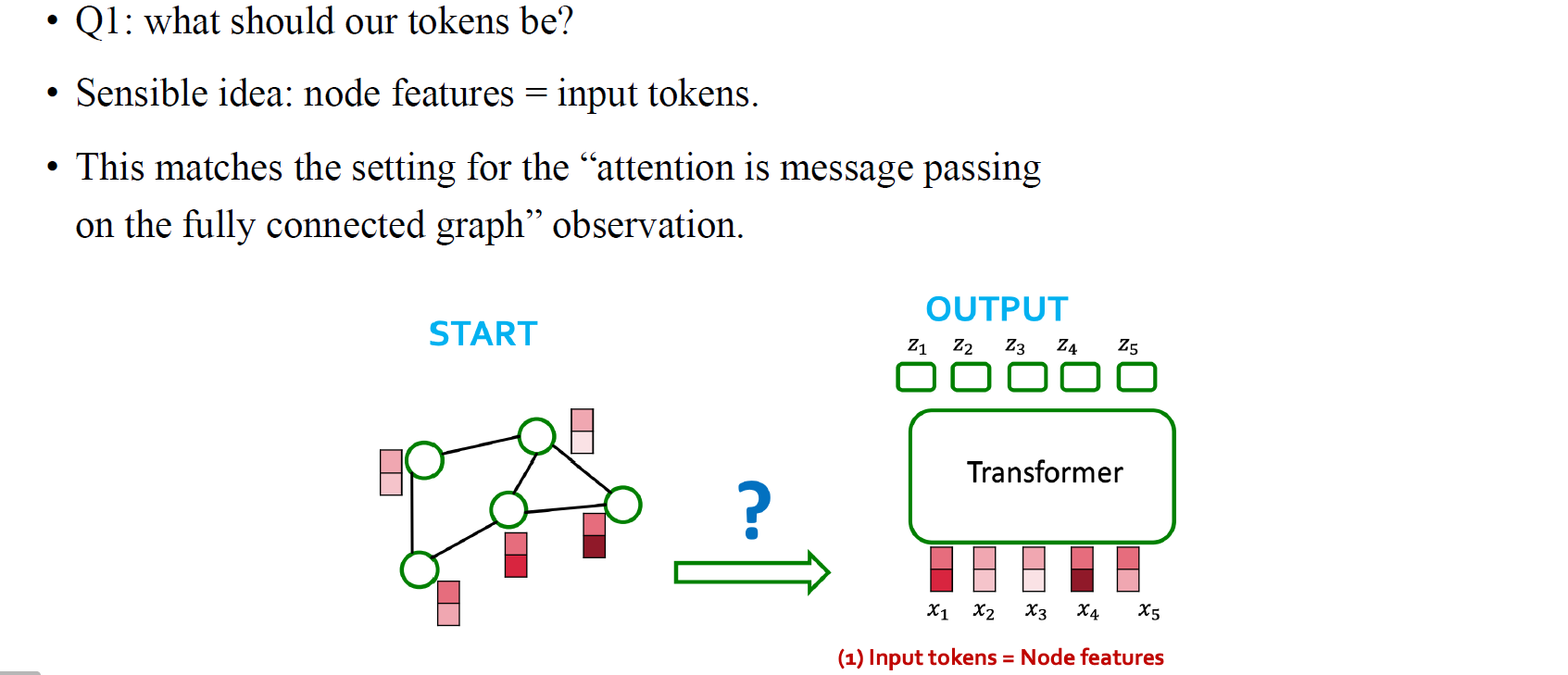결국, node feature를 text data에서 word와 같다고 생각하면 node feature를 input token으로 해석하게 된다. 하지만 단순히 node feature를 token으로 넣어주기만 한다면 text에서와 처럼 단어들의 위치 정보를 잃어버리는 큰 문제로 연결될 것이다.

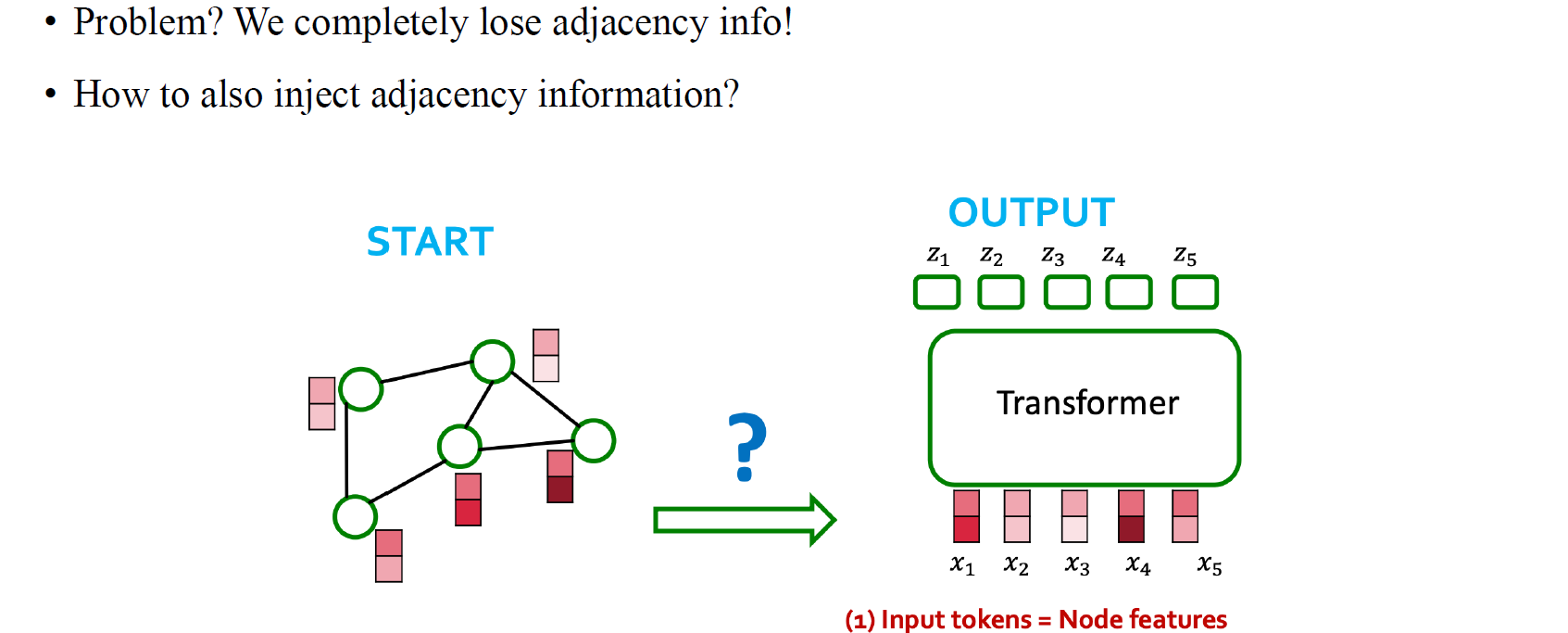그래서 graph를 transformer에 넣기 위해서 node별 feature를 넣어주는 것 외에도 edge feature인 adjacency 정보를 추가로 넣어주기도 한다. 이렇게 정보들을 모델에 넣어주는 방법들이 최근 많이 연구되어지고 있다.

How to Add Back Adjacency Information?

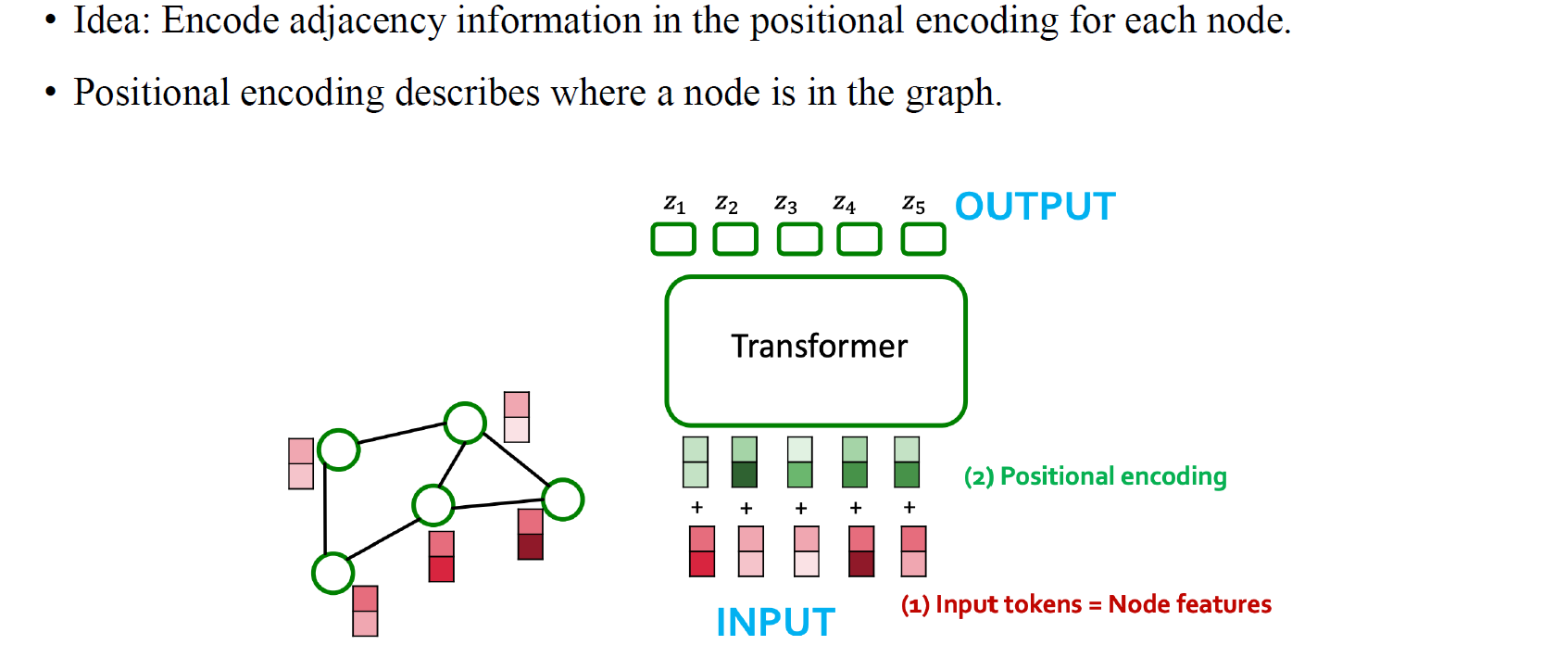여기까지 정리해보면 우선 node feature를 transformer에 사용하기 위해서 positional encoding을 추가함으로써 input feature를 바꿔줘야 한다. 이렇게 여기에 adjacency information을 추가로 넣어주고 싶은 것이다. 만약에 graph를 sequential data와 같이 보자면 각 node마다 하나의 위치 정보를 부여받을 것이다. 이러한 방법이 sequential data에 positional encoding을 하는 간단한 방법일 것이며, 각 숫자가 결국 각 node의 위치가 되는 것이다.

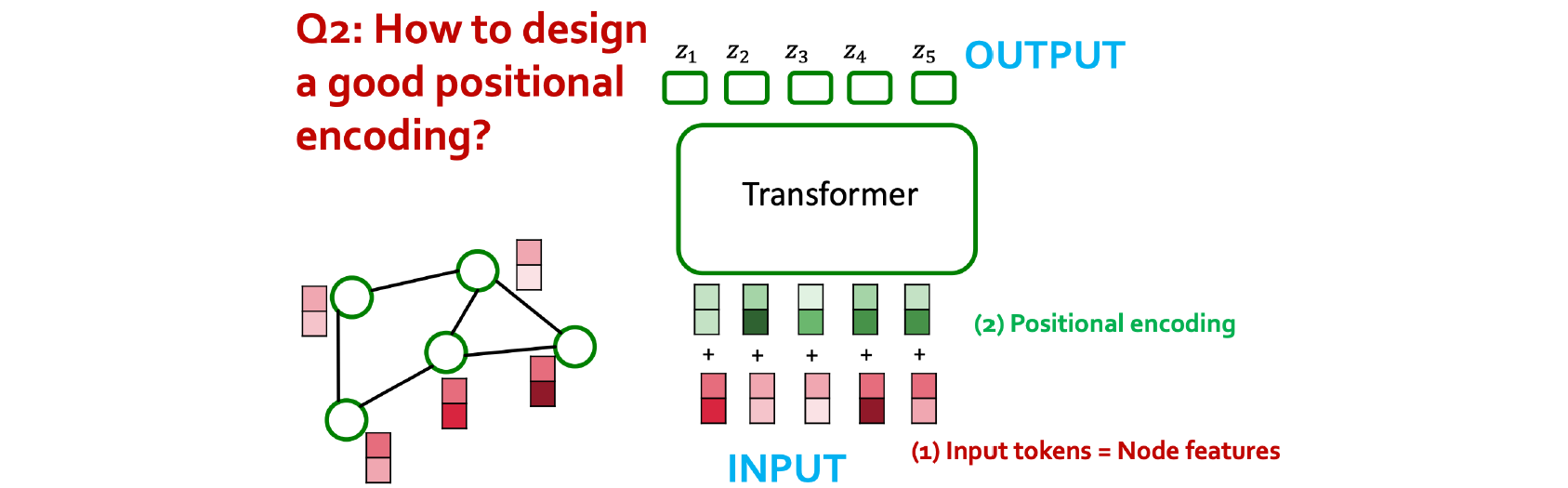여기까지 봤으면 한가지 이상한 점을 생각할 수 있을 것이다. Graph에서 어떻게 순서를 정의하는지가 문제가 될 것이다. 그러나 위치가 고정된 graph라면 node들은 고정된 순서가 있을 것이다. 그렇기 때문에 각 node마다 graph 안에서 어떻게 위치 정보를 가질 수 있는지 표현할 수 있는 방법을 생각해야 한다. 사실 positional encoding이라고 하면 결국 node를 embedding으로 바꿔주는 하나의 방법일 수는 있다. 결국 positional encoding이 되었다면 우리는 graph 안에서 각 node들의 위치를 알 수 있을 것이고, 이로부터 각 node들을 전부 구분할 수 있게 될 것이다. 이는 결국 node embedding 알고리즘으로 정의된다고 볼 수 있다. 사실 가장 흥미로운 정보를 담고 있는 순서대로 positional encoding을 해도 상관이 없다.

Laplacian Eigenvector Positional Encodings

사람들은 결국 graph에서 node의 위치 정보를 반영시키는 하나의 방법으로 Laplacian eigenvector positional encoding을 생각했었다. Laplacian matrix는 결국 하나의 graph를 설명할 수 있고, 해당 graph의 구조를 encoding할 수 있다. 그렇기 때문에 graph마다 존재하는 Laplacian matrix는 각각의 graph의 다른 점을 설명할 수 있게 된다.

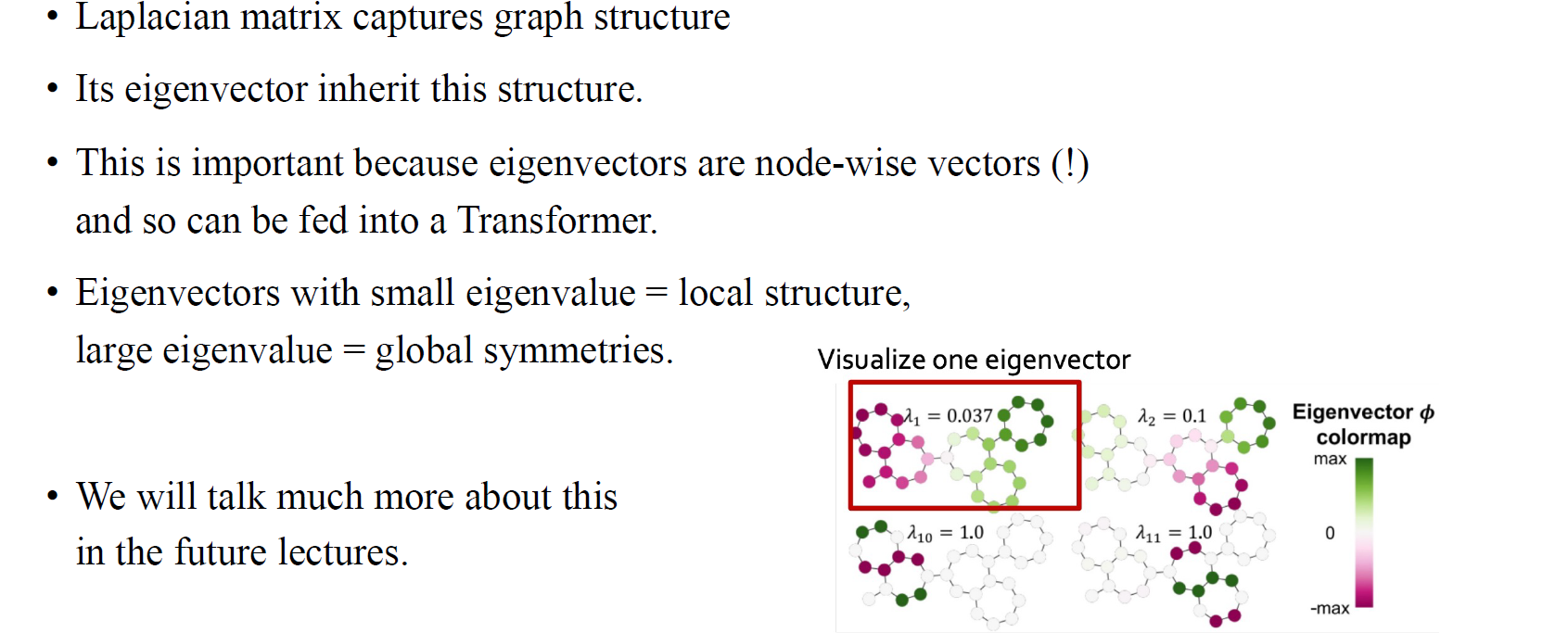만약 Laplacian matrix $L$로부터 eigen-decomposition을 통해서 eigenvector를 구하게 된다면, 이는 node embedding algorithm이 될 수가 있다. $L$로부터 얻은 eigenvector와 eigenvalue의 개수는 총 node의 개수와 동일할 것이고, 각각의 eigenvector는 모든 node에 대응되어 존재하게 된다. 여기서 $L$의 eigenvalue는 node embedding algorithm으로 사용되어 주어진 graph에 대해서 positional encoding이 가능해진다.

Adjacency matrix를 제곱하여 분해하여 얻은 eigenvector는 node feature로 사용될 수 있다. 마찬가지로 Laplacian eigenvector positional encoding도 마찬가지로 node feature를 얻는 방법으로 볼 수 있다. 그리고 우리는 이를 이용해서 graph transformer의 positional encoding으로 사용할 수 있다. 흥미로운 부분은 각 eigenvector에 대응되는 eigenvalue에 따라서 graph 구조를 파악할 수 있다는 것이다. 여기서 다룰 내용은 아니지만 간단하게 이야기하면 eigenvalue가 작은 경우에는 graph의 local한 정보에 더 초점을 맞추고, 반대로 eigenvalue가 큰 경우에는 graph의 global한 정보에 더 초점을 맞출 수 있다.

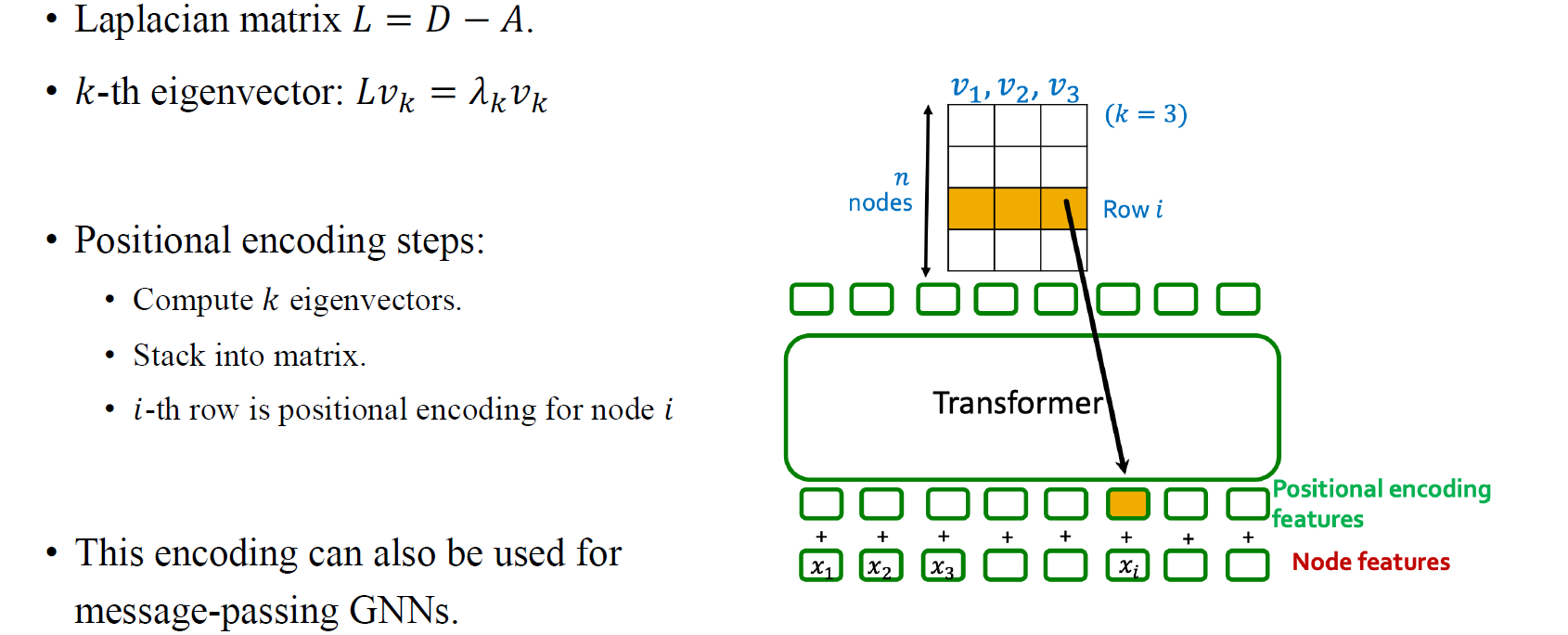우리는 총 $k$개의 eigenvector가 있다면, 이들을 전부 stacking하여 하나의 matrix를 구성하고 동일한 위치에 있는 값들로부터 새로운 벡터를 형성하여 각 node별 feature로 만들 수 있다. 이렇게 eigenvector를 이용한 positional encoding 방법이 처음으로 graph transformer를 변형시킨 사례가 되었다.

Shortest Path Encoding

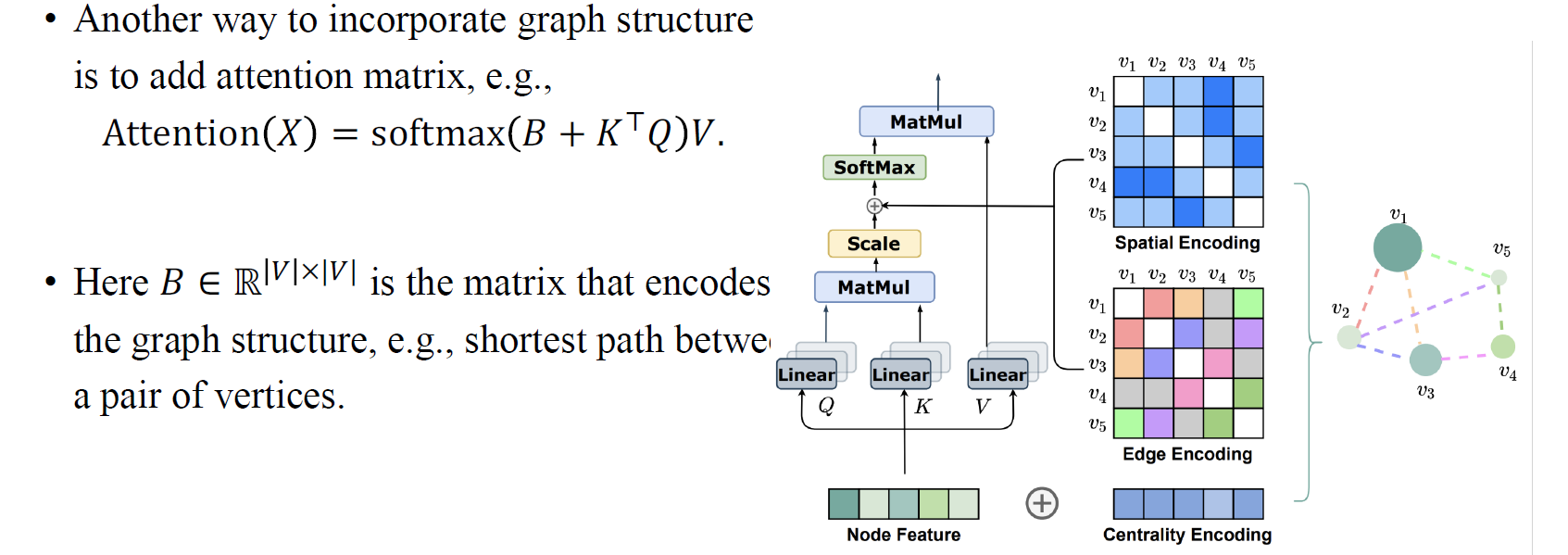이외에도 하나의 사례를 더 살펴보면 shortest path encoding이 있다. 이 방법의 아이디어는 모든 transformer가 값들을 mixing하는데서 시작하게 된다. 이 과정에는 node-wise feature transformation이 동반되는데, 이 방법이 하고자하는 것은 attention matrix를 adjacency matrix를 기반으로 해서 만들고자 하는 것이다. $Q$와 $K$의 matrix multiplication 과정에서 graph의 구조를 통합하고자 했을 떄, 이들의 multiplication 결과와 graph의 구조 정보를 담고 있는 특정 matrix를 더해서 attention matrix를 구해주는 것이다. 가령, 각 node 사이의 shortest path 결과를 담고 있는 matrix를 더할 수 있을 것이다. 이렇게 graph의 구조 정보를 통합하여 attention matrix를 설계하는 것이 좋은 성능으로 연결된다는 것을 사람들을 발견했다.