Why Manipulate Graphs
GNN을 다루기 앞서 왜 graph를 manipulation해야 하는지 알아야 한다. 지금까지 우리가 GNN에 넣을 graph를 처리한다고 했을 때, 예를들어 molecular graph나 community graph 등을 파악하기 위해서 GNN에 해당 graph를 넣는다고 가정했을 때, 우리는 raw input graph를 computational graph로 가정하게 된다. 이말이 무엇인지 이해하기 위해서 molecular graph가 있다고 가정해보자. 우리가 GNN에 이러한 특정 분자 구조의 graph를 넣는다고 했을 때, 모델은 우리가 분자 구조에 대해서 이해하고 있는 식으로 동일하게 graph를 받아들이지 않게 된다. GNN에 graph를 넣기 위해서는 기존의 graph의 정보가 충분치 않아 온전히 사용하기 보다는, 여기에 임의의 vertex나 임의의 edge를 추가하게 된다. 이러한 식으로 보조적인 정보를 추가하면서도 동시에 기존의 정체성을 유지시키는 것이 바로 manipulation의 핵심이다. 이는 이미지에서의 data augmentation과 같은 맥락으로 이해할 수 있다. 정리해보면 우리가 feature-level manipulation이 필요한 이유는 input graph의 정보가 충분치 않기 때문에 expressive power를 증가시켜주기 위해서 이러한 feature augmentation을 동반해주는 것이다.
여기에 추가적으로 structure-level manipulation도 존재한다. 가령 GNN이 다루기에 graph가 너무 sparse한 경우에는 효과적으로 message passing을 할 수 있도록 만들어야 할 것이다. 반대로 graph가 너무 dense하다면 조금 sparse하게 만들 필요가 있을 것이고, graph가 너무 크다면 이를 작게 잘라서 사용해야 할 것이다.
Feature Augmentation
Graph의 feature manipulation은 매우 직관적이다. 일반적으로 graph는 adjacency matrix와 node feature matrix로 구성이 되지만, node feature matrix가 없는 경우에는 일반적으로 해당 graph에 cycle이 존재하는지 분류하는 task를 수행하게 된다. 이러한 경우에는 graph에서 모든 vertex가 동일하기에 node feature와 관련이 없게 된다. 그래서 graph에 가상으로 node feature를 만들어주고 사용할 수가 있다. 사람들은 GNN을 사용하기 위해서 graph에서 임의로 각 vertex의 어떠한 상수를 부여해서 auxilary node feature로 사용했다. 대표적인 방법 중 하나로는 각 vertex의 node degree를 feature로 만들어서 사용하는 것이다.
사람들은 또 다른 방식으로 각 vertex에 독립적인 ID를 부여해서 사용하곤 했다. 위와 같이 6개의 vertex에 1~6까지 임의의 숫자를 부여한 뒤 이를 one-hot encoding을 거쳐서 node feature로 만들어주는 것이다. 이는 symmetric graph를 다룰 때는 굉장히 도움이 많이 되는 방식일 것이다. GNN이 각 vertex를 구별해야한다면 이렇게 독립적인 ID가 부여되어 있다면 graph를 파악하기 용이할 것이다. 따라서 unique ID는 expressive power를 쉽게 올리는 방법 중 하나로 많이 사용된다. 하지만 임의로 ID가 부여된다면 GNN의 학습에 있어 generalization의 측면에는 문제가 있을 것이다. 예를 들어 6개의 vertex를 GNN이 학습했는데 7개의vertex를 가진 graph를 평가해야 한다면 새로운 ID를 봐야하기 때문에 일반화에 어려움이 있을 수 있다.
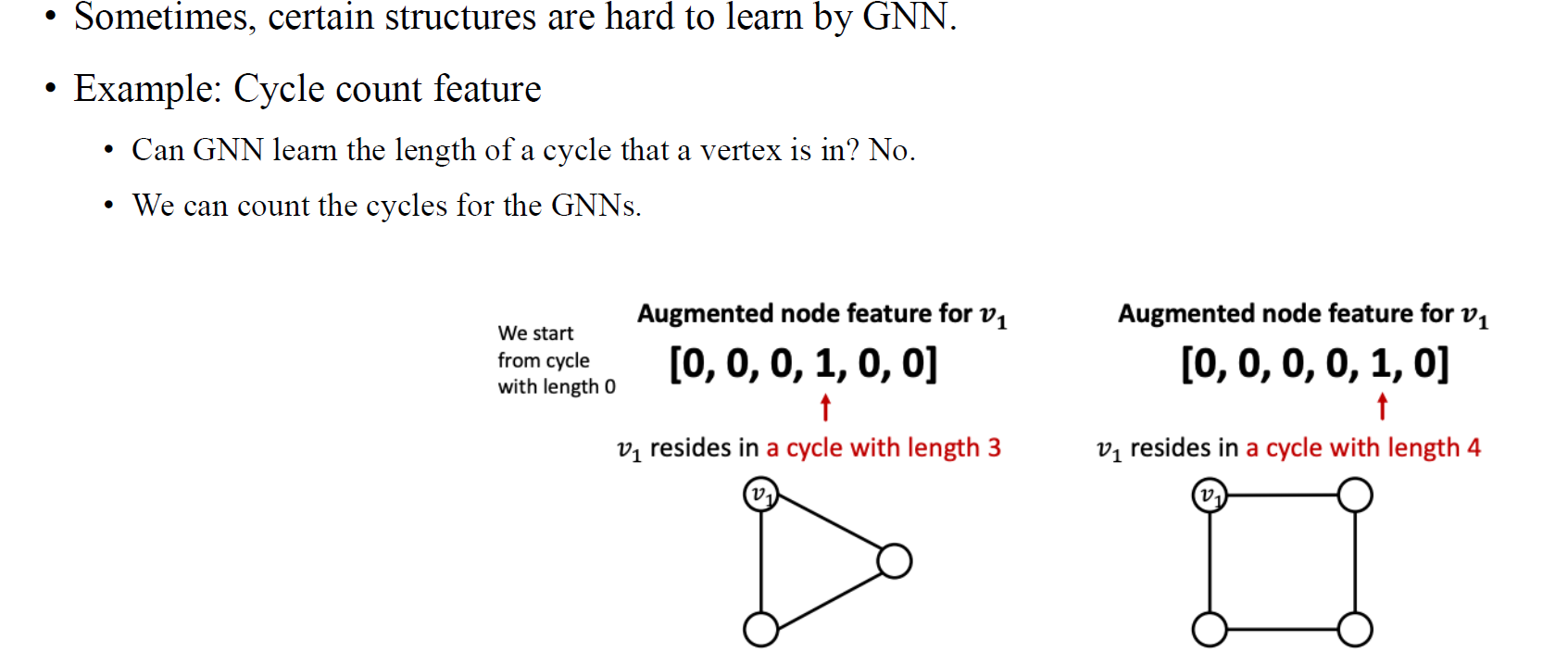Expressive power를 올리는 또 다른 feature augmentation 방법 중 하나는 cycle count feature를 사용하는 것이다. 예를 들어 graph가 길이가 3인 cycle을 가지고 있다면 해당 vertex에 길이가 3인 cycle을 가지고 있다는 정보를 one-hot feature로 부여할 수 있을 것이다. 길이가 4인 경우에도 마찬가지일 것이다. 이것이 매우 중요한 이유는 사람들이 GNN이 graph의 cycle 개수를 셀 수 없다는 것을 증명했기 때문이다. 그 이유는 GNN의 message-passing 방법이 매우 지역적이기 때문에 cycle의 개수를 세는 능력이 부족하기 때문이다. 그렇기 때문에 단순히 이렇게 cycle의 수를 feature로 추가해주기만 해도 GNN의 representation 능력이 더 늘어나게 될 것이고, 이로 인하여 graph를 더욱 잘 파악할 수 있게 될 것이다.
Structure Augmentation
Adding virtual edges
지금까지 feature augmentation에 대해서 알아봤는데, 많은 경우에서 sparse한 graph를 augmentation하기 위해서 virtual edge를 추가할 수도 있다. 이는 매우 중요한데, 예를 들어서 매우 긴 graph나 매우 큰 graph를 가정해보자. GNN layer가 5개만 있어도 전체 graph를 파악할 수 있는 간단한 graph가 있다고 생각해보자. 여기에 2-hop neighbor를 연결시킬 수 있는 virtual edge를 추가할 수 있게 된다면 똑같이 전체 graph를 파악하는데 있어 더 적은 layer만 필요할 것이다. 만약 graph가 너무 sparse하면, 즉 edge의 수가 매우 적다면, 이렇게 2-hop neighbor를 연결할 수 있는 virtual edge를 추가할 수 있을 것이다. 또 다른 예로 위와 같이 author-to-paper로 구성된 bipartite graph가 있을 때, author 사이에 가상의 edge를 추가하여 author collaboration non-bipartiet graph를 만들 수도 있을 것이다. 이렇게 edge를 추가하는 행위가 결국에는 GNN이 graph를 파악하는데 도움이 될거라는 믿음에서부터 시작되는 것이다.
Adding virtual nodes
Virtual edge를 추가할 수 있다면, 같은 목적으로 virtual node도 추가할 수 있을 것이다. 만약에 모든 node를 연결하는 virtual node가 존재한다고 가정하면, GNN은 멀리 떨어진 두 node의 정보를 모으기 위해 propagation을 많은 layer를 통해서 거치지 않고도 virtual node로 인하여 정보를 얻을 수 있게 될 것이다. 반대로 가까운 node들에 대해서는 많은 layer를 쌓지 않고도 정보를 모을 수 있을 것이다.
Node neighbor sampling(dropout)
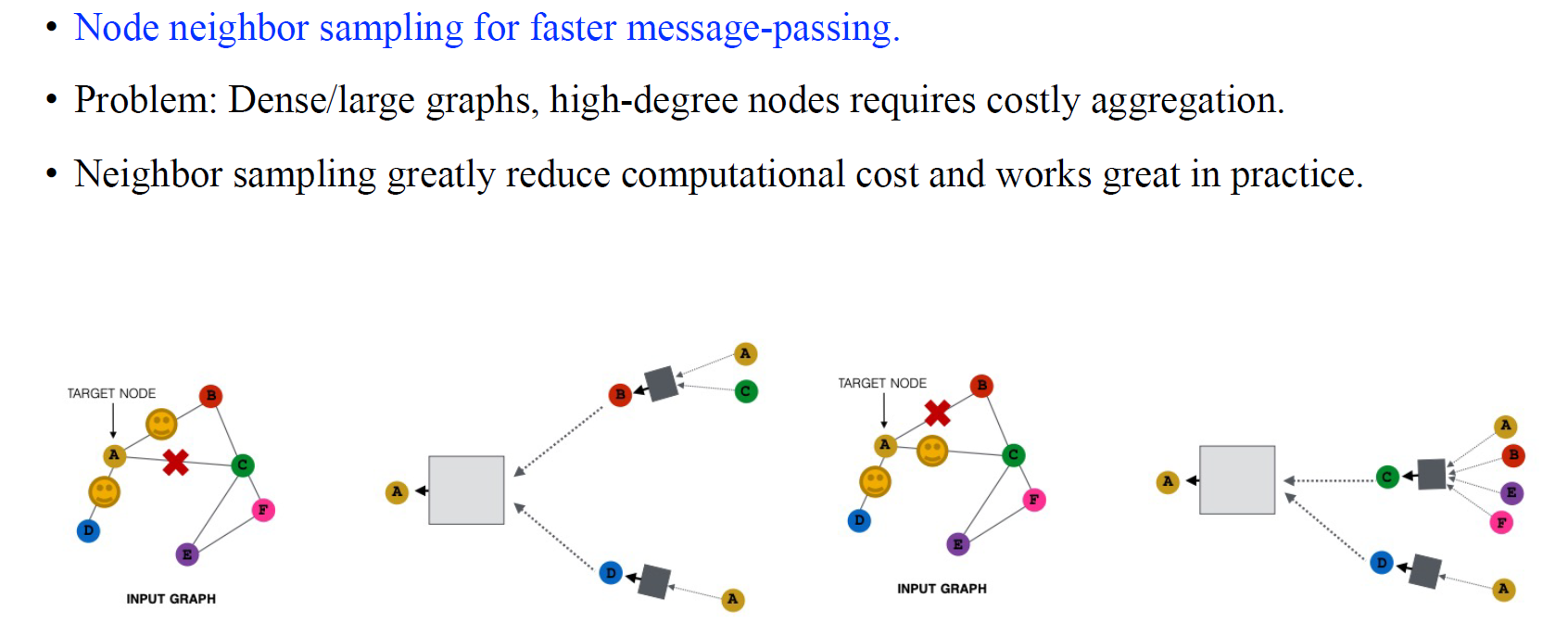마지막으로 structure augmentation에는 node neighbor sampling 혹은 node neighbor dropout이 있다. 만약 web graph처럼 매우 많은 vertex로 이루어진 graph가 있다면 GNN은 이를 전부 사용하기 힘들 것이다. 그래서 이렇게 큰 graph를 파악하고자 GPU에 fitting 하려면 일부 정보는 버려야 할지도 모른다. 이를 수행하기 위해서 전체 graph에서 몇몇 edge를 제거해야 할 것이고, 이렇게 되면 더욱 sparse한 graph를 얻게 될 것이다. 이는 computation cost를 줄일 수 있으며 실제로는 이렇게 neighbor의 정보를 버리는 것은 효과적일 때가 많다. 이러한 이유로 인하여 structure augmentation은 더욱 강조가 된다.
지금까지 graph manipulation에 대해서 살펴보았는데, 이정도의 내용만 제대로 숙지하고 있어도 GNN을 사용하는데 충분하다고 할 수 있다.
