[그래프 기계학습] Significant GNN Architectures

Significant GNN Architectuers

이번에는 2021년도까지 약 10년 동안 중요하다고 생각되는 몇몇 GNN들에 대해서 알아보고자 한다.

Generalization of CNN to Graphs

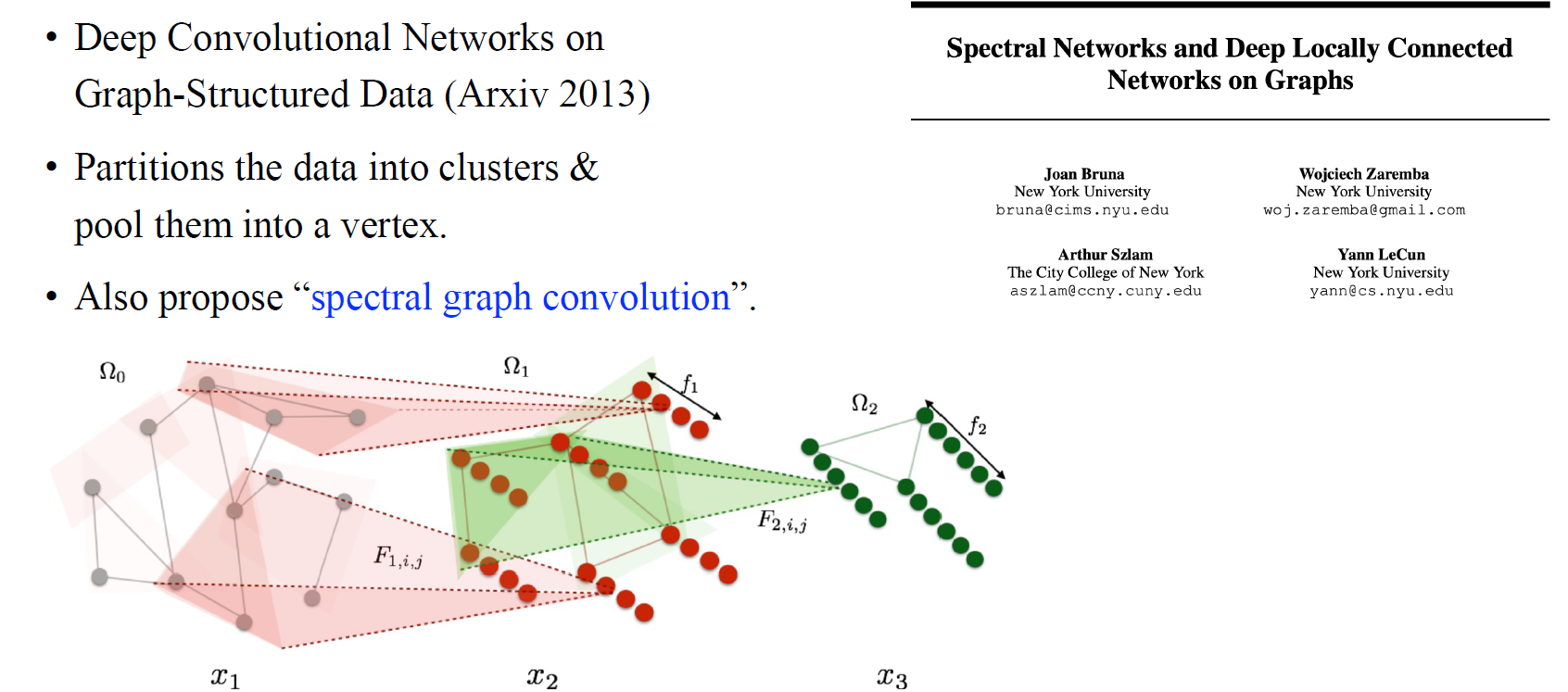가장 먼저 우리는 GNN의 역사에 대해서 알고싶기 때문에 사람들이 알게 된 맨 처음 GNN이 무엇인지에 대해서 알아볼 필요가 있다. 사람들이 흔히 알게 되는 GNN은 2016년부터라고 생각할 수 있지만, 그 이전에 2013년도에 Yann LeCun 그룹에서 위와 같은 논문을 제공했다. 이들은 GNN으로부터 receptive field를 늘리거나 각 layer에서 vertex의 수를 줄이는 과정을 위해서 여러 vertex들을 가지고 cluster를 형성하고 이들을 새로운 neuron으로 처리했다. 이렇게 얻어진 coarse grained graph를 가지고 계속해서 propagation을 해나가면 유사하지만 작은 graph를 만들 수가 있게 된다. 이들은 사람들이 "spectral graph convolution"이라 불리는 방식 또한 제안했으며, 이는 graph signal processing에서 가져온 개념이다. 이렇게 이들은 GNN의 첫번째 접근법을 제안했었다. 이후에도 약 3년간 여러 방식들이 제안되어 왔지만, 이들은 대부분 3d mesh data 등에 적용된 방법들이기 때문에 더 중요한 다음 논문을 보고자 한다.

ChebNet

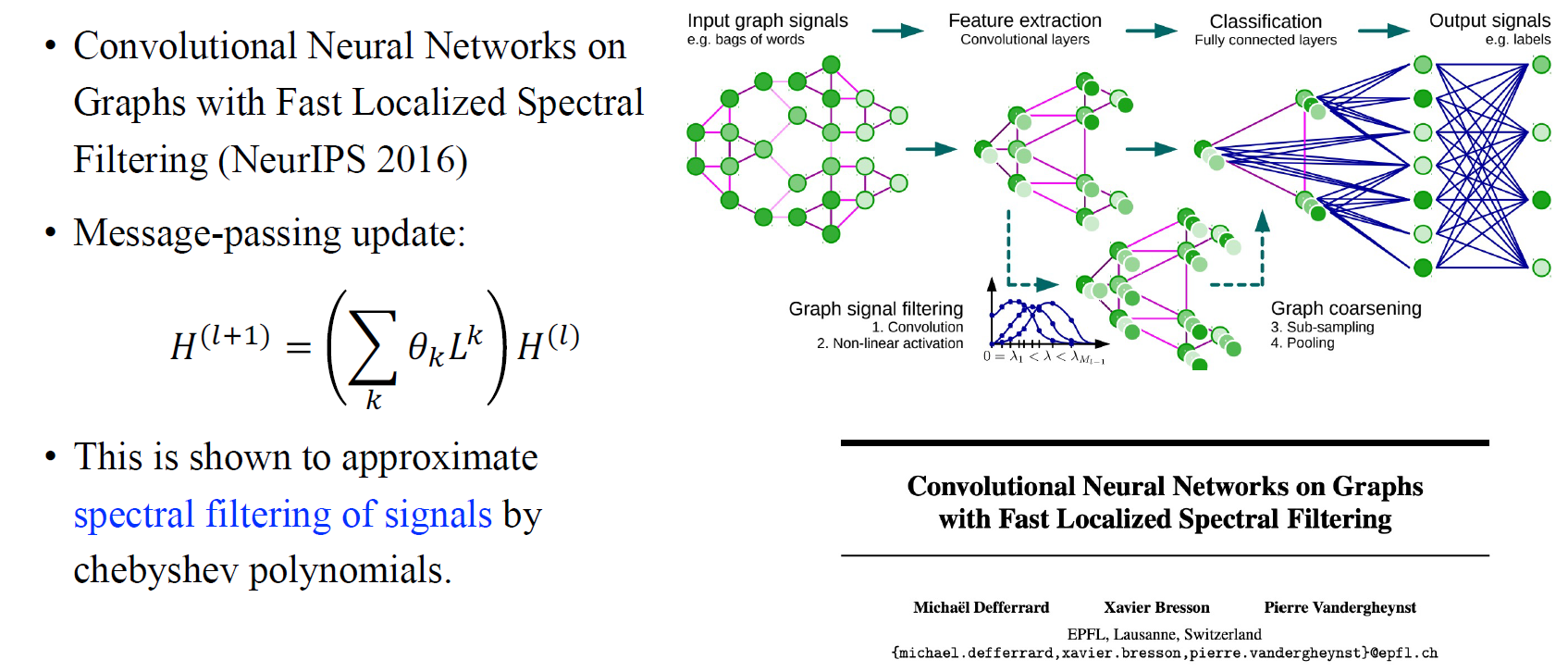NeurIPS 2016년도에 ChebNet이라고 하는 GNN의 새로운 접근 방식이 제안되었다. 이 논문은 graph signal의 spectral filtering의 대표적인 예시 중 하나이기 때문에 매우 중요하다고 이야기할 수 있다. 먼저 hidden feature matrix가 주어졌다고 가정해보자. 여기서 하고자하는 것은 degree matrix와 adjacency matrix를 이용하여 $D-A$로 계산되는 laplacian matrix $L$을 구하고, 이를 $k$번 곱하는 것이었다. 각각의 $L$에 weight vector $\theta_k$를 곱하고 $k$번 더함으로써 이를 parameterization하고자 한다. 저자들은 graph signal processing community에 속한 사람들이 말하는 graph convolution이 이 논문에서 말하는 과정과 같기 때문에 이와 같은 과정들이 매우 중요하다고 이야기했다.

Spectral Graph Convolution

그렇다면 spectral graph convolution이 무엇일까? 먼저 spectral이라고 말하는 것은 matrix의 eigen-decomposition과 관련이 있다. 따라서 spectral graph convolution은 laplacian matrix의 eigen-decomposition을 기반으로 한다. $L$에 eigen-decomposition을 하면 $U\Lambda U^{-1}$로 만들 수 있고, spectral graph convolution은 실제로 $U(\sum\Lambda^{k}) U^{-1}$에 의해 정의된다. 우리는 이 과정을 $L$을 $k$번 곱하는 과정으로 생각할 수 있어서, 결국 중간의 $U$와 $U^{-1}$는 지워지기 때문에 $L^k=U\Lambda^{k} U^{-1}$가 된다. 결국 위와 같은 식은 eigen-decomposition의 parameterization을 한 것으로, 사람들은 이 과정을 spectral graph convoltuion으로 표현될 수 있다고는 것을 알았고 이 과정은 또한 time signal의 Fourier transformation과 연결되게 된다.

결국 지금까지 소개되었던 두 논문은 spectral graph convolution을 spatial graph convolution으로 정의하여 neural network를 만들게 된 것이다. 실제로 GNN community에서도 GNN의 역사를 크게 spectral GNN과 spatial GNN으로 나누었으며, spectral GNN에서는 message-passing을 통해 얻는 일련의 과정을 signal processing community에서 말하는 것을 따라갔었다. Fourier transformation으로부터 사람들은 graph signal processing을 따라 convolution을 얻는다고 생각했기에 결국 graph Fourier transformation과 graph convolution은 이러한 원칙적인 방법으로부터 얻게 되었다.

Graph Convolutional Network (GCN)

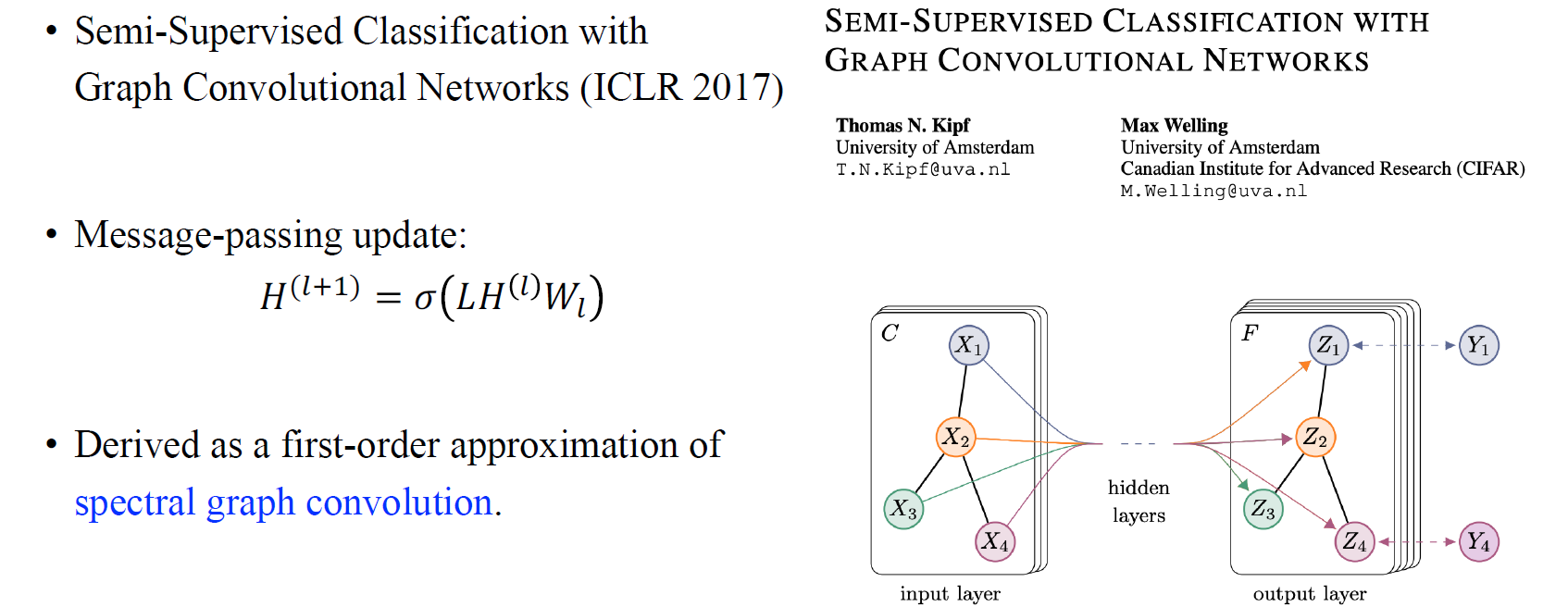이후에 사람들은 또 다른 접근 법으로 GNN을 표현하게 되었고, 대표적인 예시가 바로 graph convolutional network (GCN)이다. 이 논문은 아마 GNN 연구에 있어 가장 많은 인용수를 기록하는 논문일 것이고, 사람들이 GCN이라고 흔히 불리는 논문이다. 이는 매우 유명한 message-passing update 과정으로 laplacian matrix와 feature matrix, weight matrix를 곱한 결과에 non-linearity를 주었다. 이 논문을 보면 알겠지만, 단순히 이러한 message passing 과정이 main contribution이 아닐 것이다. 이 논문의 main contribution은 이러한 message-passing update가 있는데, 이러한 과정이 우리가 이전 논문들에서 언급되었던 spectral graph convolution이라 불리는 과정의 first-order approximation으로 얻어지게 된다는 것이다. 이 논문 이후로 사람들은 spectral한 접근 보다는 이러한 방식의 message passing 과정을 선호하게 되었다.

Message Passing Neural Network (MPNN)

GCN은 ICLR 논문으로 봄에 출판되었으며, 사람들은 이 논문을 빠르게 읽은 뒤에 GNN 연구들을 계속해서 제안했다. 대표적으로 quantum chemistry에 대한 neural message passing 방법을 새로 제안하게 되었다. 사람들은 분자 구조를 파악할 수 있는 GNN 연구를 했으며, 이러한 유명한 message passing 방법들을 적용해서 분자의 quantum chemical property를 approximation하려고 시도했다. 그렇게 등장한 GNN이 바로 message passing neural network (MPNN)이다.

GraphSAGE

뒤이어 해당년도 NeurIPS에는 GraphSAGE라는 방법이 제안되었고, 이 저자들은 큰 knowledge graph나 database에 초점을 맞췄다. 저자들이 제안한 GraphSAGE는 large graph를 처리하기 위한 방법으로 message-passing update를 더욱 시스템적인 방법으로 접근한다. 따라서 이들은 다양한 조합의 aggregation과 message update를 수행하게 된다. 또한 이들은 scalability를 위해서 neighbor들을 drop하는 것도 제안했으며, 지금까지 사람들이 많이 사용하는 고전적인 Weisfeiler-Lehman (WL) isomorphism test라고 불리는 방법에서 영감을 얻어 만들어지게 되었다.

Relational GCN

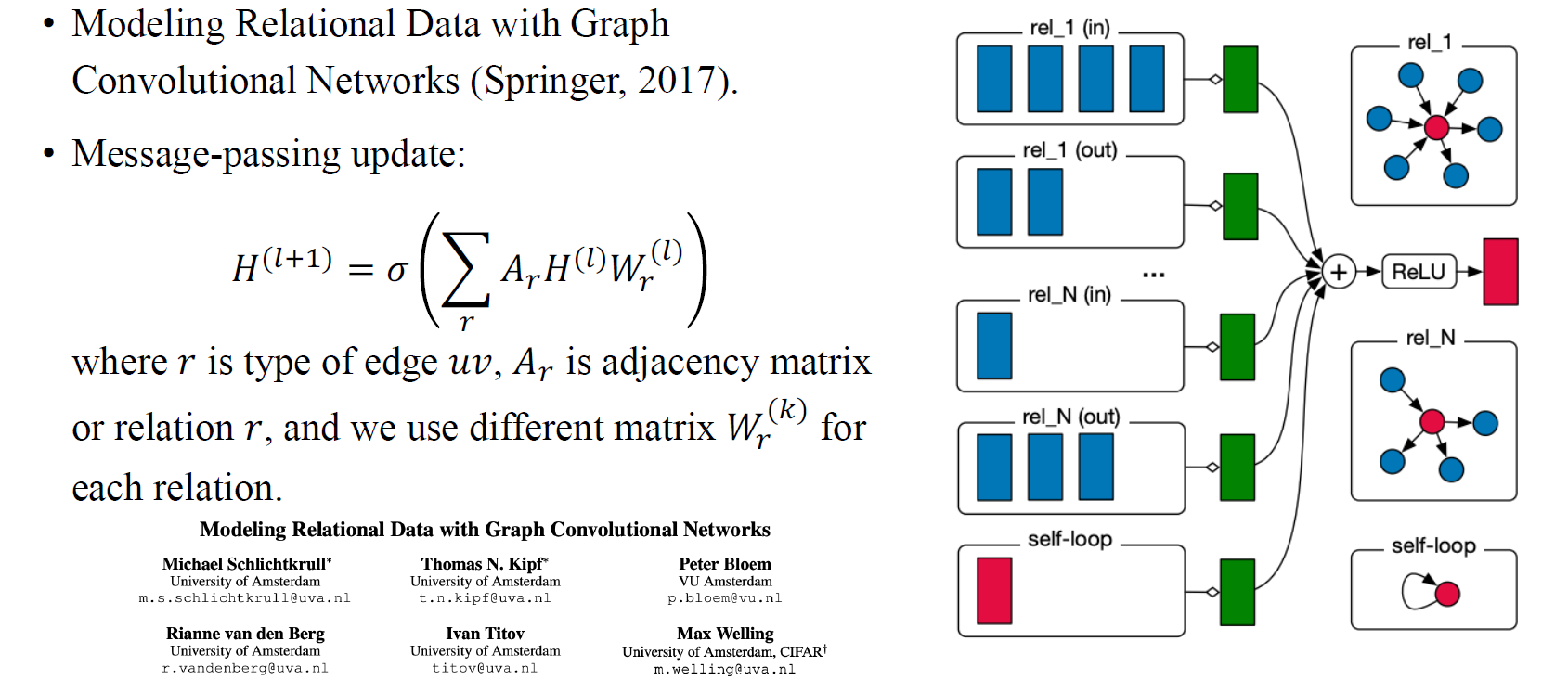Edge에 relation이 있는 graph에 대한 방법으로 Relational GCN이 등장하기도 했다. 각 edge type 혹은 relation에 따라 서로 다른 adjacency matrix를 이용해서 message-passing update를 하는 것이 이 방법의 핵심이다. 예를 들어 우리가 $N$ relation이 있다고 가정했을 때 $N$개의 graph를 만들 수 있으며 각각의 $N$개의 graph마다 message-passing update를 수행할 수 있고, 마지막으로 이들을 합쳐서 결과를 만들 수 있게 된다. 이때 흥미로운 부분은 $N$개의 adjacency matrix가 있는 만큼 $N$개의 weight matrix도 있다는 것이다.

GatedGCN

또 다른 GNN으로 GatedGCN이 있다. 여기서 저자들이 하고자 했던 것은 message-passing update를 할 때 두 node 쌍 사이의 hidden feature에서 gating mechanism을 수행하는 것이다. 두 node의 hidden feature와 edge 사이의 gating mechanism을 통해서 조건을 주는 것이다. 이러한 방법이 graph attention network에서의 attention mechanism과 유사하게 보일 수 있다.

Graph Attention Network (GAT)

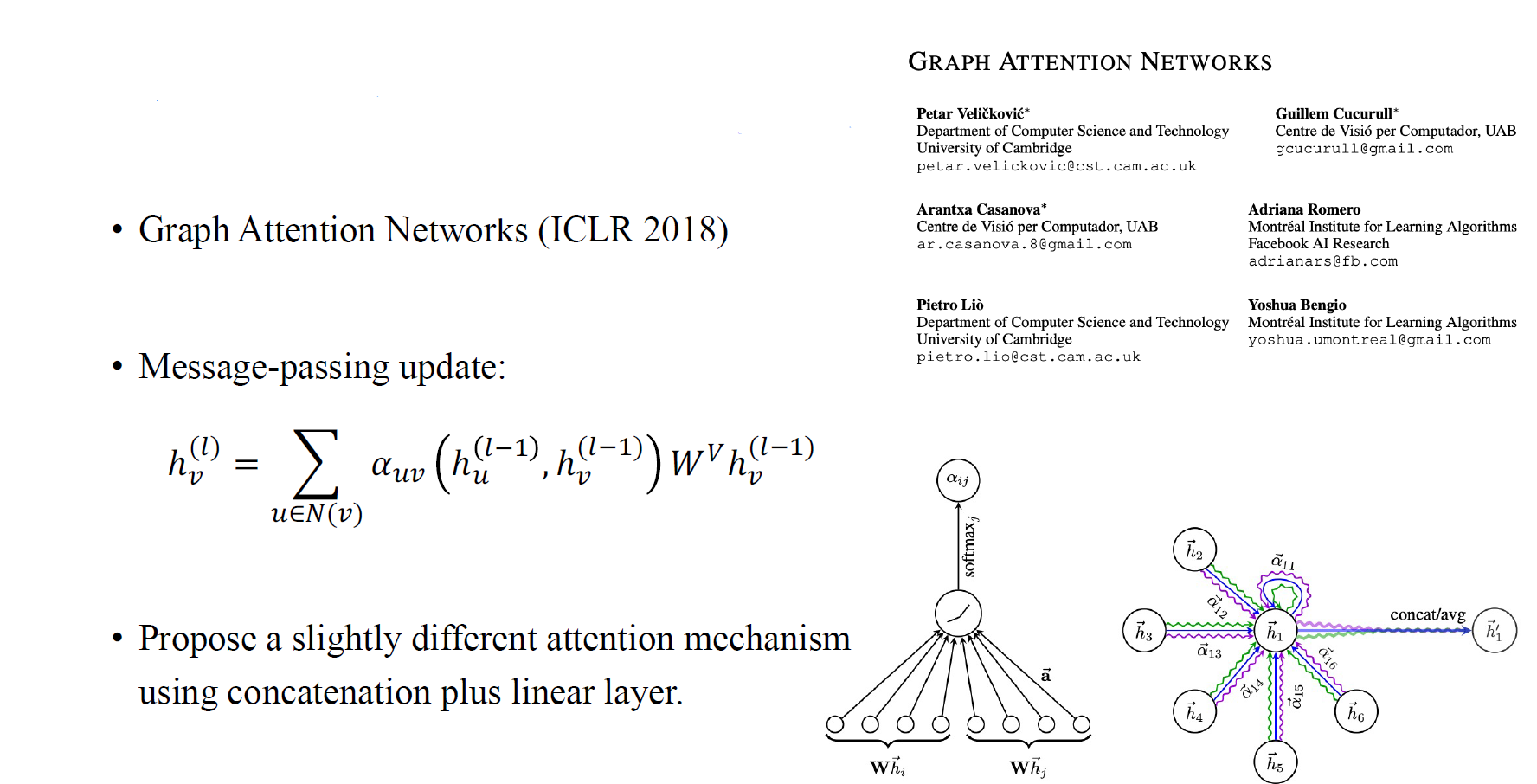GatedGCN과 동일한 년도에 동일한 학회에는 유사하지만 유명한 graph attention network (GAT)가 제안되었다. Message-passing update시 $\alpha$가 두 node 쌍에 일종의 attention을 부여하게 된다. 이들이 제안한 vertex들을 concat하고 linear layer와 뒤따르는 softmax function을 처리하여 attention matrix를 얻는 방식은 전통적인 attention mechanism 방식과는 약간의 차이가 있다. 전통적인 방식에서는 vector간 dot product를 계산하지만, 여기서는 concatenation이 필요하다고 제안했다.

Jumping Knowledge Network (JK-Net)

2018년도에는 jumping knowledge network (JK-Net)이 등장하였다. 아이디어는 residual layer를 GNN에 이용하기 것이기 때문에 매우 간단하다. 비록 아이디어가 상대적으로 간단해보일 수 있지만, 사람들인 이 방법이 놀랍도록 강력하다는 것을 알게 되었다. 연속되는 layer에 residual layer를 연결하는 것 대신에 가장 마지막에 있는 layer에 모든 residual을 연결하는 것이 이 논문의 아이디어이다. 이렇게 얻어진 결과로부터 concat, max pooling 등의 layer aggregation을 하게된다. Random walk에 기반한 추가적인 이론 해석이 있기 때문에 사람들은 이 방법이 얼마나 중요한지 알게되었다. Vertex들 사이에 local information이 message-passing을 거치는 동안 사라지기 때문에 이러한 정보들을 보존하기 위한 residual connection이 상당히 중요해지는 것이다.

Graph Isomorphism Network (GIN)

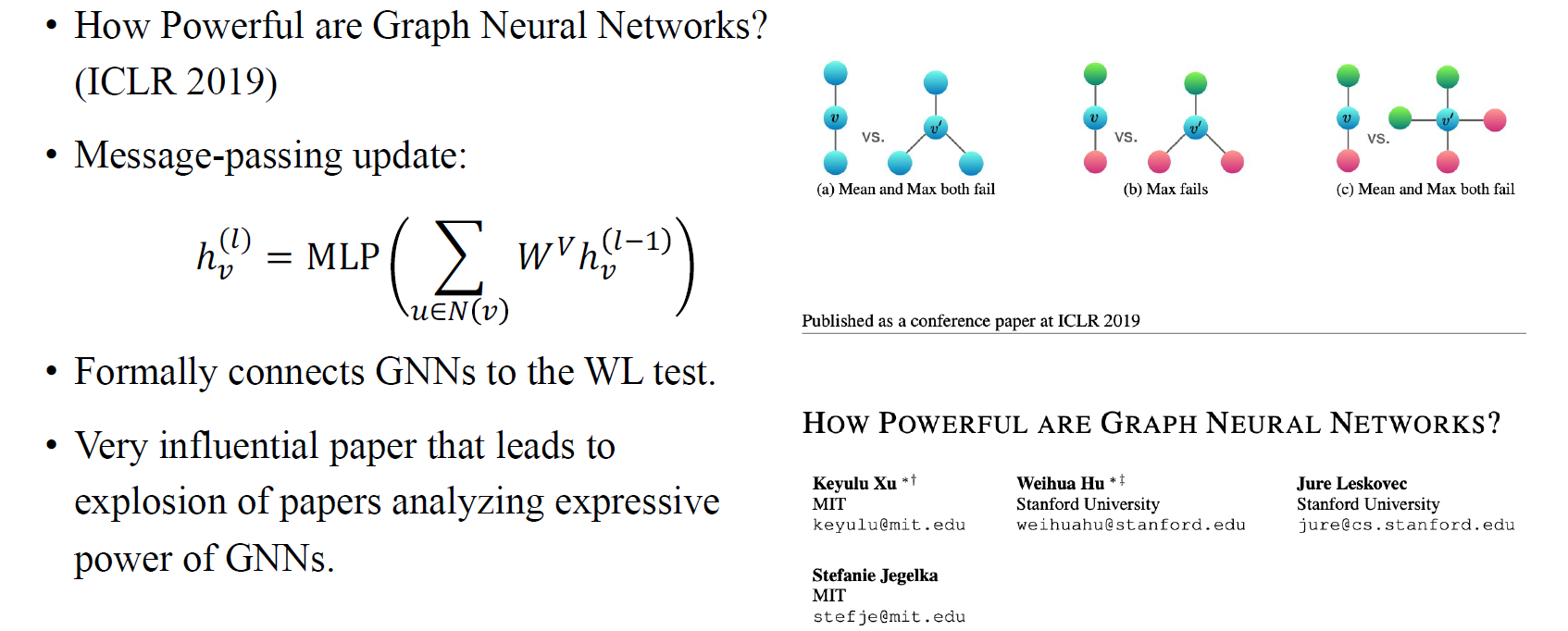다음으로는 GNN을 분석하는데 있어 가장 중요한 방법인 graph isomorphism network (GIN)이 등장하였다. 여기서 저자들은 얼마나 GNN의 expressive power가 얼마나 강력한지에 대한 분석을 적어놨다. 이를 위해서 graph isomporphism test에 의해서 GNN의 expressive power를 정량화할 필요가 있다고 주장했다. 예를 들어 2개의 이웃한 vertex를 가지는 서로 다른 2개의 graph가 있다고 해보자. 만약 GNN이 두 graph가 다르다고 주장하게 된다면 해당 GNN은 강력하다고 할 수 있다. 반대로 두 graph가 다르지 않다고 말하는 GNN도 존재할 것이다. 이러한 test를 graph isomporphism test라고 하며, 이 논문은 GNN이 이러한 test를 통과할 수 있는 능력을 정량화했다.

더불어 이 논문의 흥미로운 아이디어는 aggregation step에서 linear update를 하기 이전에 aggregation을 위한 mean pooling을 해왔다는 것에서 시작한다. 실제로는 이웃들의 aggregation을 위하여 sum operator를 사용하기 때문에 message를 update하기 위해서는 MLP를 사용해야 한다고 주장했다. 그리고 GNN과 WL test 사이의 connetction에 의해서 이 방법이 GNN에 더 강력한 expressive power를 제공하게 된다. 그렇다면 이 방법이 왜 더욱 강력함을 보장해줄 수 있는지 생각해보자. 예를 들어 이웃간 mean과 max pooing을 한다고 했을 때 만약 2개 혹은 3개의 동일한 vertex가 있다면 여기에 mean pooling을 했을 때 단지 같은 값을 가져오게 될 것이다. 하지만 반대로 sum pooling을 한다고 해보자. 그러면 우리는 이웃한 vertex들이 2개든 3개든간에 다른 vertex가 있다는 것을 확인할 수 있게 된다. 이렇게 mean pooling과 sum pooling의 차이로 부터 우리는 서로 다른 vertex가 존재함을 파악할 수 있는 것이다. 이 논문은 처음부터 끝까지 WL관련 test로 분석되어 있기 때문에 GNN 논문을 작성할 때 일종의 레시피로서 역할을 할 수 있고, 그에 따라 굉장한 영향력을 행사할 수 있었다.

Simplifying Graph Convolution (SGC)

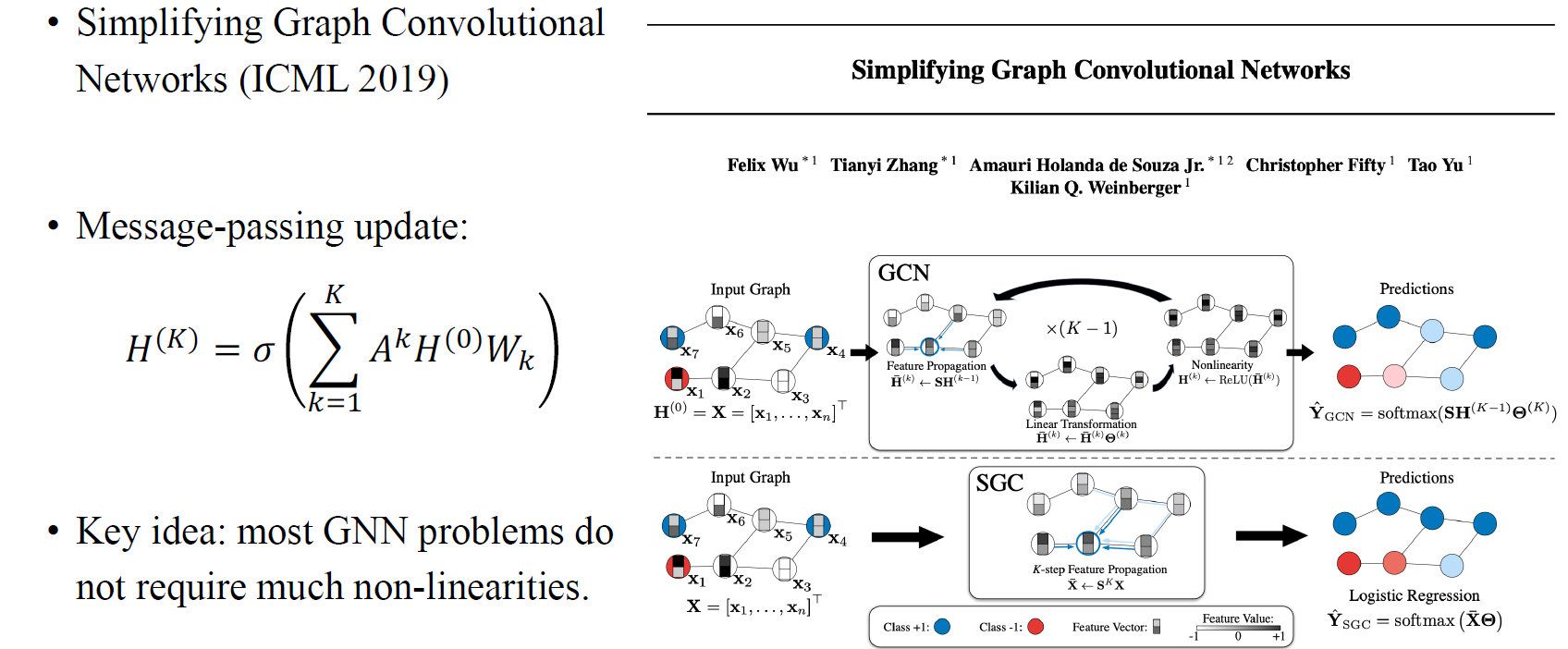다음은 simplifying graph convolution (SGC)라는 논문으로 2019년도에 ICML에 제안되었다. 지금까지 사람들이 GNN의 expressive power를 높이기 위해서 matrix multiplication을 이용한 여러 message-passing 방법들을 제안해왔다면, 이 논문에서 저자들은 실제로 데이터셋을 살펴보았을 때 많은 GNN layer가 필요하지 않다는 것을 주장했다. 사람들은 GNN을 더욱 복잡하게 만들거나 정교하게 만들려고 노력해왔었지만, 이 논문에서는 데이터셋이 그만큼 복잡하지 않고 간단하기 때문에 GNN을 복잡하게 만들 필요가 없다는 이야기를 했다. 여러개의 non-linearity를 적용할 필요 없이 하나의 non-linearity만 적용하면 된다고 주장했고, 여기에 adjacency matrix는 여러번 곱하는 것을 이야기했다. 이전의 GCN이 feature propagation, linear transformation, non-linearity를 부여하는 과정을 여러번 수행했다면, SGC의 아이디어는 $k$번의 feature propagation을 한번만 수행하고 마지막에 non-linearity도 한번만 주면 된다는 것이다. 이 방법은 매우 간단하지만 GCN이나 다른 복잡한 방법들보다도 매우 강력한 결과를 만들었다.

여기서 혼란스러워하면 안되는 부분으로 GIN은 linear-message-linear-message에서 message passing을 스킵하는 식으로 동작하고 여기에 MLP를 이용해서 더 많은 non-linearity를 부여하는 식으로 GNN을 더욱 강력하게 만든다면, SGC는 non-linearity를 지움으로써 overfitting을 방지하고 더 빠르게 동작할 수 있음을 이야기하는 것이다.

Principal Neighbourhood Aggregation (PNA)

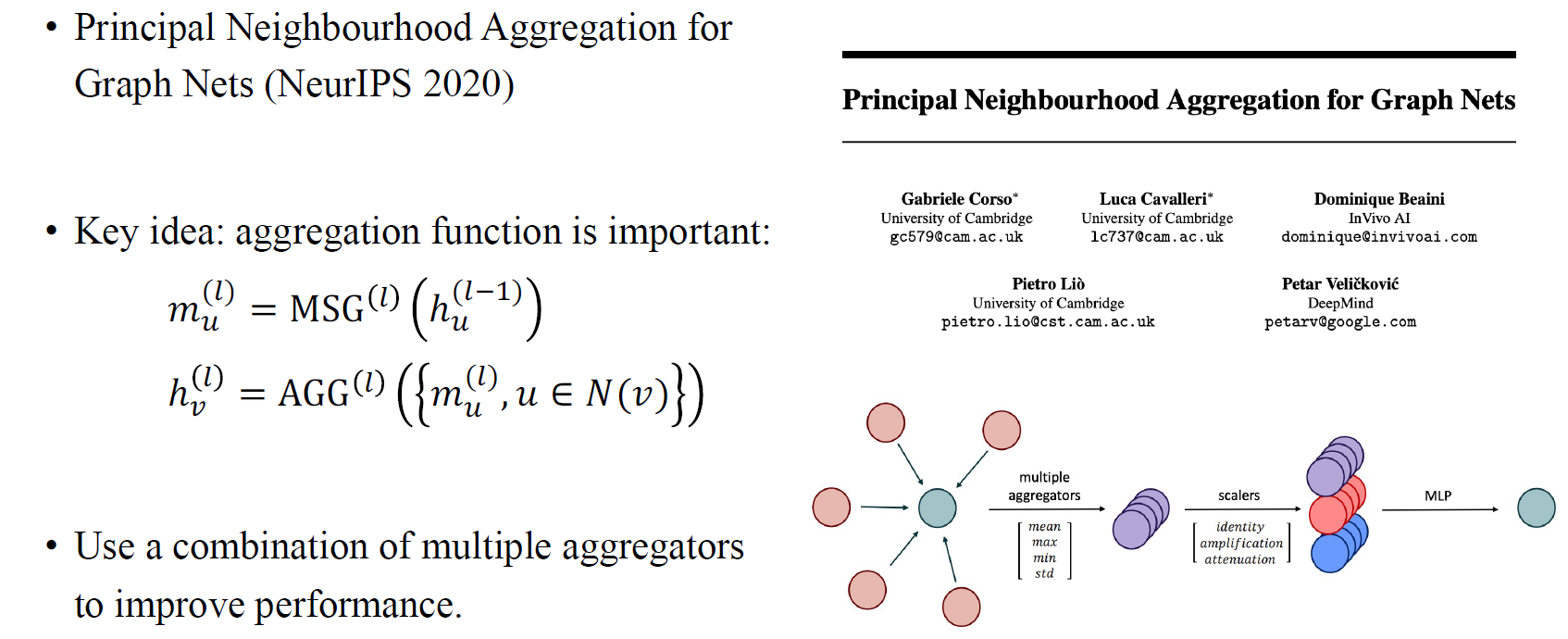NeurIPS 2020년도에 제안된 principal neighbourhood aggregation (PNA)는 어떻게 aggregation function을 선택해야 하는지를 이야기하고 있다. 이들은 하나의 aggregation을 사용하기 보다는 mean aggregation operator와 max aggregation operator 사이에서 선택할 수 있다고 말했다. 또한 분산이나 표준편차도 permutation에 invariant하기 때문에 이러한 것들도 aggregation의 방법으로 선택할 수 있다고 했다. 우리는 vertex의 degree로부터 function을 만들 수 있어서, aggregation 결과에 아무것도 하지 않거나 exponential을 곱하거나 하는 식으로 최종 aggregation 결과를 만들어 MLP에 통과시킬 수 있다. 이렇게 하나의 aggregation 방식이 아닌 여러 aggregation 방식을 통해서 성능을 올릴 수 있다는 것이 PNA가 주장하는 바이다.

GCNII

해당 년도에 ICML에는 simple and deep graph convolutional networks라는 GCNII가 발표되었다. 대부분의 경우에 GCN layer를 많이 쌓더라도 성능을 크게 향상시킬 수 없다는 문제를 해결하고자 했다. 그래서 저자들은 간단한 trick으로 매우 깊게 쌓은 GCN에서도 좋은 성능을 낼 수 있도록 제안하였다.

Graph Trnasformer (GT)

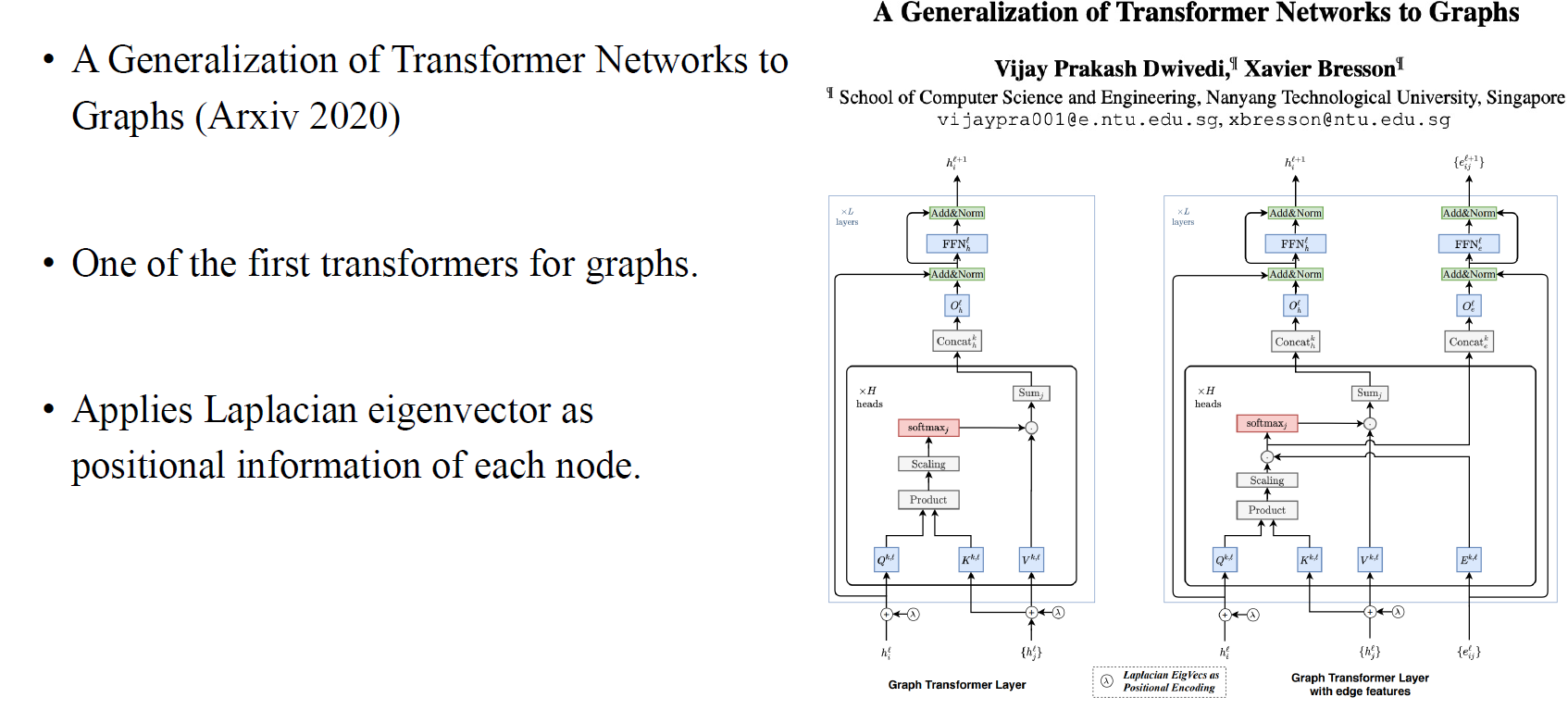이번에는 graph에 transformer를 처음으로 적용한 논문을 살펴보고자 한다. 이 논문의 핵심은 laplacian의 eigenvector를 이용해서 각 node의 positional information을 부여하자는 것이다.

Graphormer

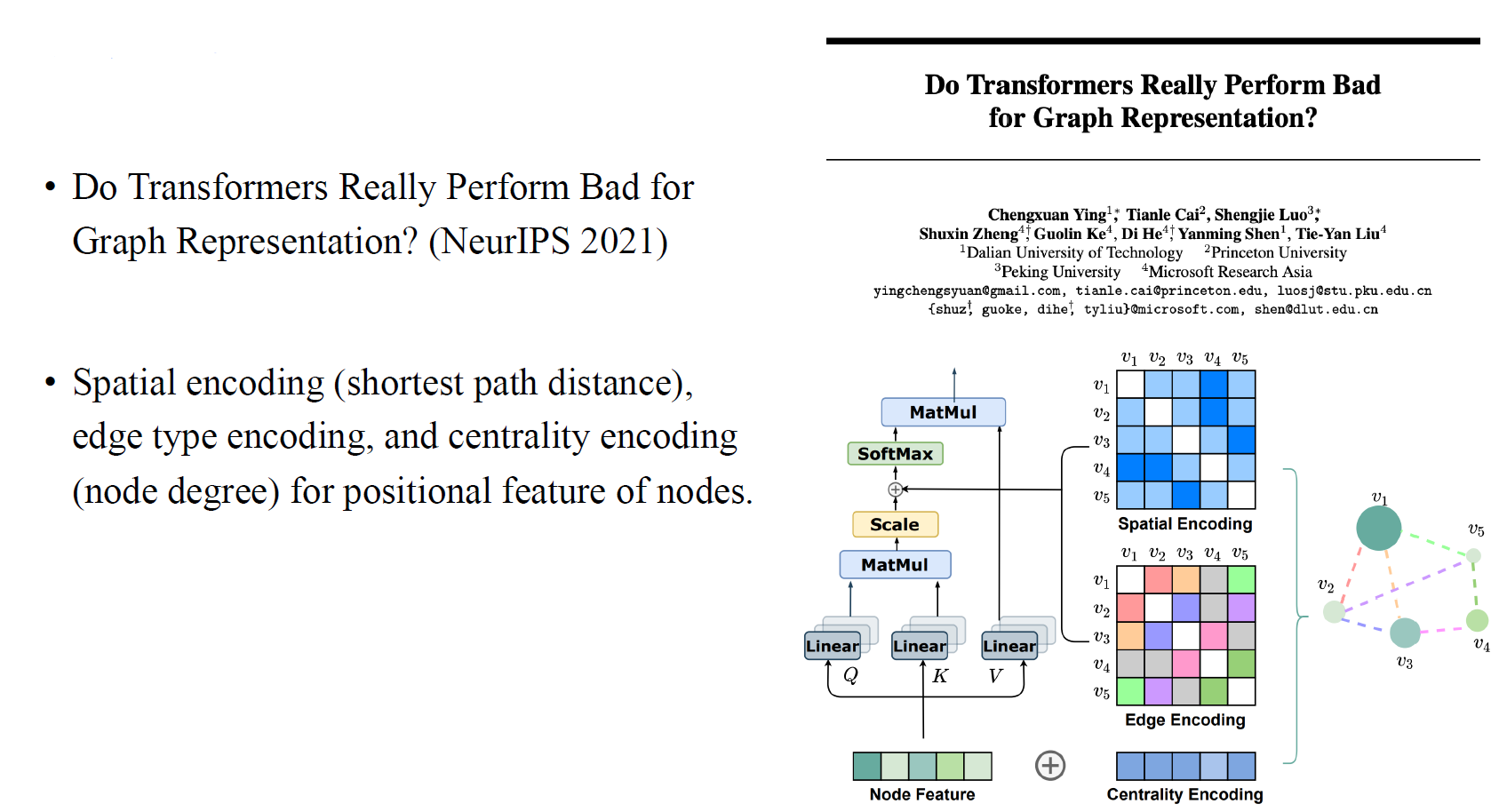그리고 graphormer의 등장으로부터 encoding 부분을 더욱 추가 함으로써 transformer를 더욱 powerful하게 만들었다. 각 vertex 쌍으로부터 shortest path distance를 이용한 spatial encoding, edge type encoding, 그리고 node degree를 이용한 centrality encoding을 이용하여 transformer 구조를 만들었다. 여기서 centrality encoding은 각 vertex가 얼마나 중심에 있는지를 나타낸다.