[그래프 기계학습] Graph Signal Processing 3

Fourier Transform

Graph signal processing 기법 중 graph wavelet transformation을 제대로 이해하기 위해서 우리는 graph domain이 아닌 signal에서의 wavelet transformation (WT)에 대해서 알아볼 것이고, 그전에 앞서 Fourier transformation (FT)부터 자세히 알아보고자 한다. WT는 결국 FT에서 시작하게 되며, FT는 모든 signal processing 기법의 기초가 되는 개념이다. FT를 이야기 하기 위해서는 period signal을 다루는 Fourier serires를 먼저 이야기해야 한다. 우리는 어떠한 period signal을 특정 sinusoidal basis를 사용해서 이를 더하는 식으로 표현할 수 있다. Period라는 개념을 finite에서 infinite로 확장하게 된다면, 우리는 이를 FT라고 부를 수 있게 된다.

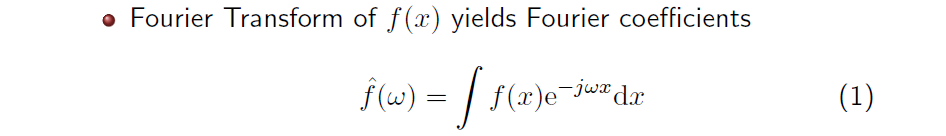$x$에 따라 정의되는 1D signal $f(x)$가 있다고 해보자. 만약 $f(x)$에 FT를 취하게 된다면 위와 같이 inner product를 구할 수가 있다. Transformation은 inner product를 하는 것과 같다고 생각하면 된다. Inner product를 통해서 $f(x)$를 sinusoidal function $e^{j\omega x}$를 basis로 하여 projection 시킬 수 있다. 여기서 $e^{j\omega x}$는 purely imaginary complex exponential로 FT의 basis로 사용이 된다. 이렇게 $f(x)$와 $e^{j\omega x}$ 사이의 inner product를 취하게 됨으로써 Fourier coefficient $\hat f(\omega)$를 얻을 수 있다. 정확한 표현이 아닐 수 있지만 여기서 integral 안에 inner product를 element-wise multiplication을 구한 뒤 summation 한다고 생각할 수 있다. 그러나 이러한 과정을 우리는 continuous space에서 하고 있어서 $x$의 space 전체에 걸쳐 $f(x)$를 $e^{-j\omega x}$와 곱하고 이를 전부 $x$에 대해서 더하게 된다. 이는 $x$에 대해서 marginalization을 하여 결과적으로 $\hat f(\omega)$를 얻을 수 있게 된다. 여기서 $\omega$는 frequency space를 설명하게 되고, Fourier coefficient에서 $f(x)$는 얼만큼의 static한 $\omega$의 frequency component가 포함되는지 정량화하는 일종의 weight로 여길 수 있다.

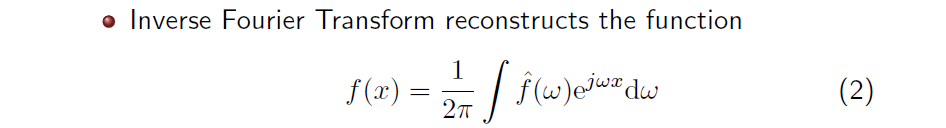이제 이렇게 Fourier coefficient가 주어진다면 우리는 inver Fourier transformation (IFT)를 수행할 수 있다. IFT는 FT와는 다른 transformation이다. IFT는 $\hat f(\omega)$를 다시 반대로 $x$로 projection하게 된다. 이 과정이 아무래도 FT의 inverse이기 때문에 동일한 basis로 $e^{j\omega x}$를 사용하고, 이를 $\hat f(\omega)$과 inner product를 구함으로써 역으로 transformation을 수행할 수 있다. 이러한 수식을 통해서 다시 $\hat f(\omega)$을 $x$ space에 projection 시킬 수 있다. 앞에 $1/2\pi$는 normalization term으로, 분모의 $2\pi$는 $e^{j\omega x}$에 내재된 scaling 값으로 생각할 수 있다. 이 식에서는 $\hat f(\omega)$와 $e^{j\omega x}$의 inner product를 coefficient와 basis간 linear combination으로 생각할 수 있고, 이를 통해서 $f(x)$를 표현한다고 생각할 수 있다. 얼만큼의 frequency component를 가지고 있는지 생각할 수 있으며, 이를 각각의 basis와 곱한 뒤 모두 더해서 $f(x)$를 구성하게 되는 것이다.

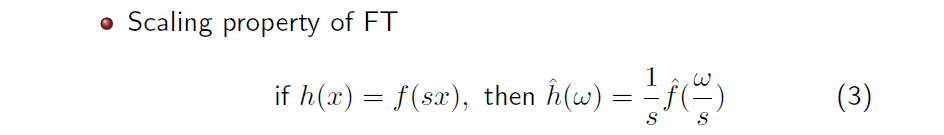그리고 FT에는 scaling property라는 것이 존재한다. 만약 $h(x)=f(sx)$일 때, 우리는 $s$를 통해서 function을 줄이거나 늘릴 수가 있을 것이다. $s$ 값에 따라서 function $h(x)$가 좌우로 더 넓어질 수도 있고 반대로 더 얇아질 수도 있을 것이다. 이제 여기서 우리가 $h(x)$에 FT를 취하게 된다면 Fourier coefficient $\hat h(\omega)$를 얻게 됨과 동시에 우변의 $f(sx)$는 $1/s\hat f(\omega/s)$로 변환이 된다. 그렇다면 이것은 무엇을 의미할까? $x$라는 space 상에서 $s$에 의해서 줄어들게 되는 signal에 대해서 FT를 취했을 때 $\omega$라는 space 상에서는 반대로 $s$에 의해서 늘어나게 되는 것이다. 이와 동시에 signal의 전체적인 magnitude도 $s$에 의해서 scaling 된다. $s$가 1보다 크다면 $\hat h(\omega)$는 작아지게 될 것이고, 반대로 $s$가 1보다 작으면 $\hat h(\omega)$는 커지게 될 것이다. 이는 $\hat h(\omega)$에서 $\hat f$ 앞의 $1/s$에 의해서 수행된다. 그리고 $s$가 scaling factor이기에 일반적으로 양수의 범위를 고려하게 된다. 그렇다면 만약 $s$가 음수가 된다면 어떠한 일이 생길까? 우리는 이 범위가 양수가 되도록 제한해야할 것이다. 물론 이 범위가 음수가 된다고 하더라도 위의 수식은 여전히 만족하게 된다. $s$가 음수라면 integral의 범위가 바뀌게 되는데, 결국에는 동일한 범위가 설정이 되어 위와 같은 결과에 도달할 것이다. 그래서 사실 $s$를 절대값으로 생각해도 괜찮을 것이고, 여기까지가 FT의 대표적인 scalining property에 대한 설명이다. 결국 요약하자면 time space에서 줄어드는 signal은 frequency space에서 늘어날 것이고, 반대로 time space에서 늘어나는 signal은 frequency space에서 줄어들게 될 것이다.

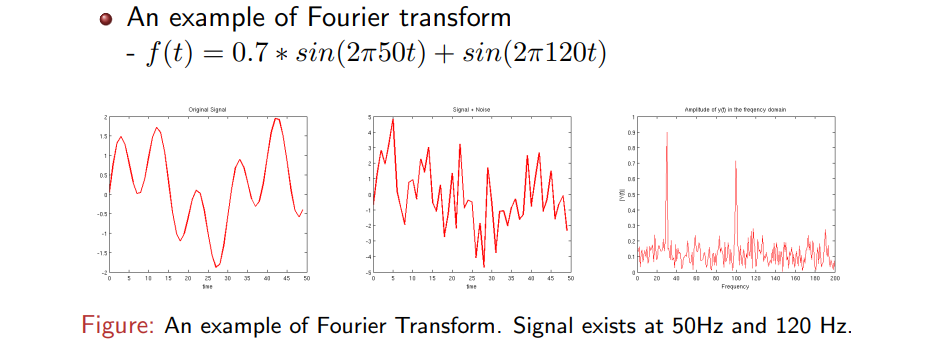위는 FT의 간단한 예시를 보여준다. 위와 같이 1D signal $f(t)$는 한눈에 봐도 2개의 sin function으로 쉽게 합쳐져서 구성된 것을 볼 수 있다. 식을 자세히보면 첫번째 sin에서 50이라는 일종의 scale이 포함되어 있고 이는 0.7의 coefficient가 곱해져 있으며, 두번째 sin에서는 120의 scale이 1의 coefficient와 곱해져 있다. 이러한 $f(t)$에 FT를 적용하게 된다면 frequency 50과 120에서 각각 coefficient 0.7과 1을 얻게 될 것이다. 그러나 문제는 항상 signal에는 특정 high frequency를 포함하는 noise가 존재하기 마련이다. 그래서 원래의 signal이 좌측과 같을 것이라면, noise가 포함이 되면 중앙과 같이 signal이 좀 더 흔들리는 모양을 보이게 된다. 그리고 여기에 FT를 취하면 우측과 같은 결과를 얻을 수 있다. FT가 우리에게 말해주는 것은 비록 원래의 signal이 noise component를 가지고 있더라도 대부분의 component는 0에 가까운 coefficient를 가지고 있으며 위의 예시에서 2개의 peak 지점의 경우에만 sin component에 해당하게 된다. 이렇게 signal이 어떻게 구성되는지 분석할 수 있기 때문에 FT는 유용하게 사용이 되는 것이다.

Limit of Fourier Transform

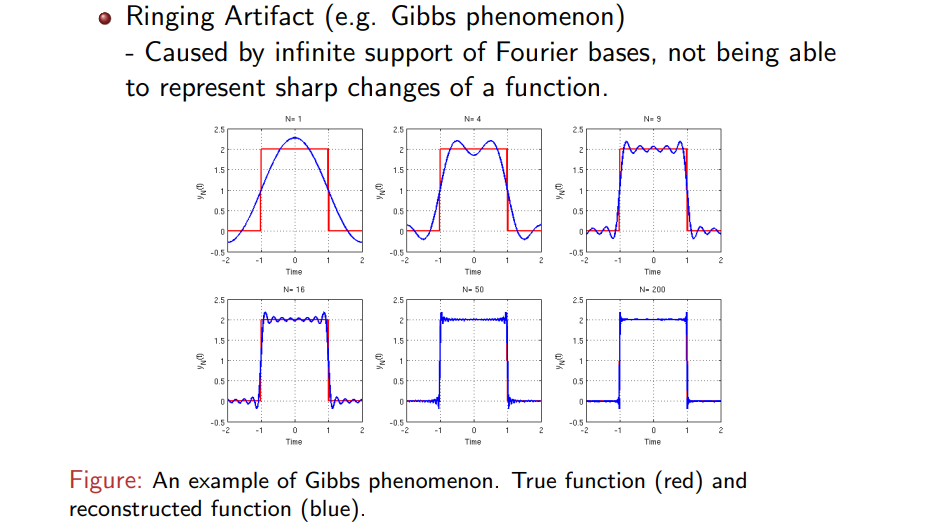그러나 이러한 FT도 완벽하지는 않다. 바로 ringing artifact 혹은 Gibbs penonmenon 때문이다. 갑자기 증가했다가 갑자기 감소하는 위와 같은 signal은 sin과 cos으로 표현하기 어려울 수 있다. 이상적으로 생각하면 가능한 경우가 존재할 수는 있다. 여기서 이상적이라는 표현은 basis의 수가 infinite한 경우를 이야기한다. 이렇게 sharp하게 변하는 function의 경우에는 FT가 최선의 transformation 방법이라고 할 수는 없을 것이다. Fourier basis들을 무한히 사용하여 원하는 function의 급격한 변화를 표현할 수 없기 때문에 발생하는 현상이 바로 ringing artifact이다. 위와 같이 basis를 무한히 사용하게 되면 원래의 signal을 비슷하게 표현할 수는 있겠지만, 현실적으로는 불가능하며 flat한 부분을 자세히보면 조금씩 벗어나는 것을 확인할 수 있다.

FT는 infinite support를 가지는 Fourier basis를 이용하며, 이는 어떠한 범위에서도 continuous한 성질을 지니고 있다. Fourier basis를 사용하게 되면 효과적으로 원래의 signal을 나타낼 수는 있지만, infinite support를 지녔기 때문에 ringing artifact를 보여준다는 한계가 분명하게 존재한다. 이러한 한계점 때문에 우리는 wavelet transformation에 대해서 알아보고자 한다.

Wavelet Transform

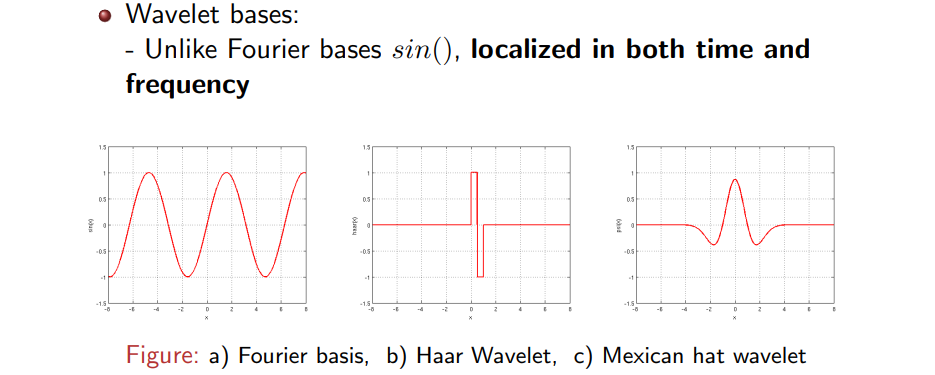Wavelet transformation (WT)은 sin과 같은 sinusoidal basis 대신에 이와 비슷하지만 다른 function을 basis로 사용하게 되며, 이를 wavelet basis라고 부를 수 있다. 좌측의 Fourier basis 대신에 중앙의 Haar wavelet basis와 우측의 Mexican hat wavelet basis는 WT에서 사용되는 대표적인 basis들이다. Fourier basis와 나머지 wavelet basis의 주된 차이점은 전자는 infinite support를 가져서 동일한 패턴이 계속해서 반복되는 반면에 후자는 highly localize 되었다는 것이다. 여기서 highly localize 되었다는 표현은 우리가 basis의 중앙이 어디인지 알 수 있다는 것이다. 중앙에서 벗어나 좌우로 이동하게 되면 그 값이 0으로 수렴하는 것이 특징이다. 이러한 특징들이 wavelet basis가 time space에서 localize 되었다는 것이고, 사람들은 또한 frequency space에서도 localize 되었다고 말하기도 한다. 그 이유는 사람들이 wavelet basis를 설계할 때 이들이 frequency space 상에서 band-pass filter가 되도록 한다. 그렇다면 band-pass filter는 무엇을 의미할까? 우리는 흔히 low-pass filter와 high-pass filter를 사용하는데, band-pass filter는 이 둘의 중간 정도로 생각할 수 있다. 즉, freuqency space에서 중간 frequency 부분들을 커버하면서 smooth하게 변하는 filter를 이야기한다. 사람들은 이렇게 bell-shaped curve 모양으로 band-pass filter를 설계해서 사용하고, 이는 frequency space 상에서 0에서 출발해서 천천히 증가하면서 큰 weight로 특정 범위를 커버한 뒤에 천천히 내려오는 형태를 보여준다. 결국 핵심은 frequency space에서 smooth하게 변하는 이러한 signal이 time space로 transformation 되면 highly localized 된 형태로 존재해야 wavelet basis가 된다는 것이다. 그래서 time space와 frequency space에서 localize 된다는 것은 time space 상에서 중앙을 특정할 수 있는 signal이 frequency space 상에서는 특정 freuency 범위를 커버하고 있다는 것과 같은 이야기인 셈이다. 이러한 점을 제외하고 FT와 WT에서 수행되는 일련이 과정에는 큰 차이가 없다.

Continuous Wavelet Transform

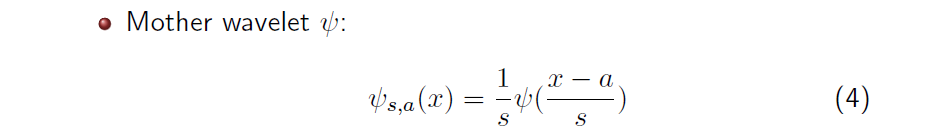FT에서는 우리가 알고 있는 sin function 등으로 basis를 사용했지만, WT에서는 wavelet basis를 미리 정의해서 사용해야만 한다. Haar wavelet이나 Mexican hat wavelet과 같이 대표적인 basis를 wavelet으로 사용해도 된다. 어떠한 wavelet을 선택해서 사용할지는 오로지 사용하는 사람에게 달려있다. 하지만, 우리가 어떠한 wavelet을 선택하더라도 위와 같이 2개의 parameter $s$와 $a$를 포함해야 한다. Mother wavelet $\psi$은 이렇게 $s$와 $a$를 포함해야 하는데, 여기서 $s$는 $\psi$의 scale을 조절할 수 있는 parameter이고, $a$는 $\psi$의 center location을 조절할 수 있는 parameter이다. 어떠한 function도 mother wavelet이 될 수 있지만, $s$를 통해서 scaling이 되어야 함과 동시에 $a$를 통해서 translation 될 수 있어야 한다.

Haar wavelet의 경우에도 dilation을 조절하는 $s$와 translation을 담당하는 $a$를 통해서 원하는대로 정의할 수가 있다. 결국 WT에서 basis로 사용이 되는 mother wavelet의 성질로는 이렇게 $s$와 $a$를 통해서 function 자체를 통제할 수 있어야 함과 동시에 frequency domain 상에서 band-pass filter의 역할을 수행해야만 한다.

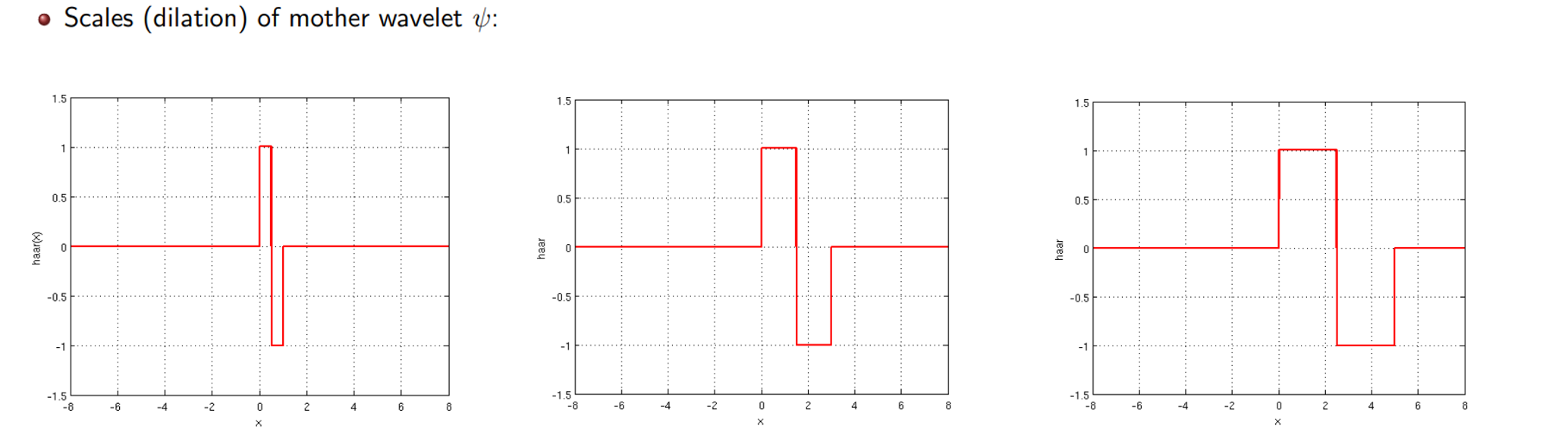그렇다면 이제 앞서 말한 parameter를 바꿔가면서 Harr wavelet이 어떻게 변화하는지 살펴보자. 먼저 dialation을 담담하는 scale parameter $s$를 바꿔보고자 한다. $s$를 바꾸게 되면 위와 같이 wavelet의 width가 바뀌는 것을 확인할 수 있다. 이러한 과정은 FT에서 sinusoidal function의 scalining과 같은 것이라고 볼 수 있고, 이를 WT에서는 scale parameter를 통해서 수행하는 것이다.

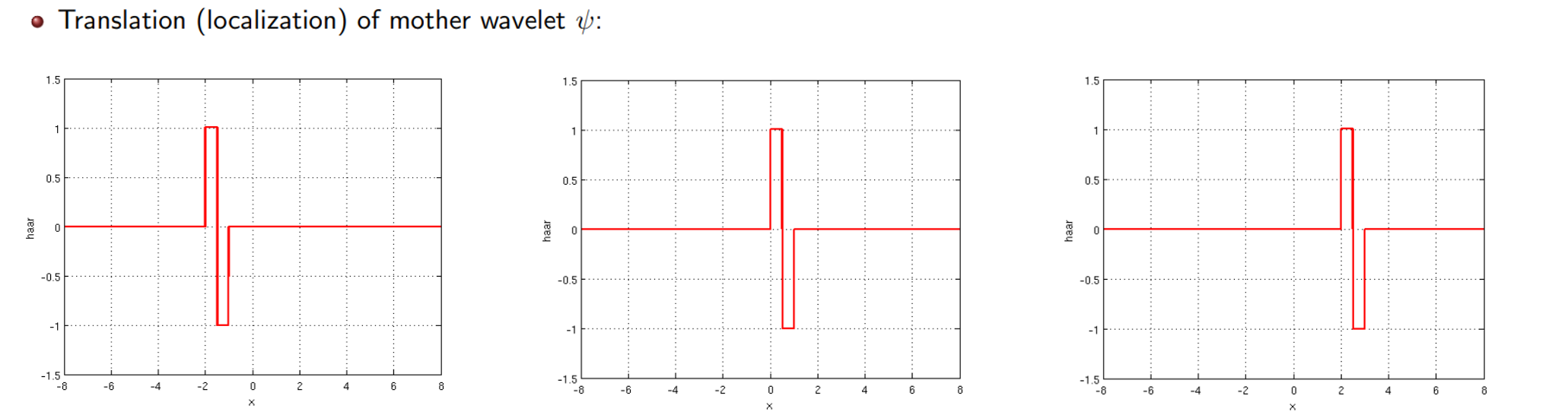$a$를 조절하게 되면 위와 같이 좌우로 center가 이동하는 것을 볼 수 있다.

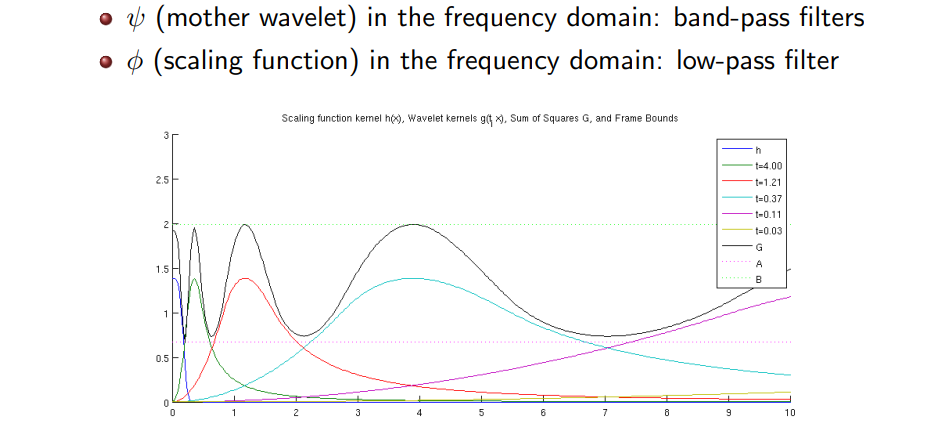위의 그림은 하나의 band-pass filter를 서로 다른 scale을 가지고 표현된 것이다. Scale parameter에 변화를 준다는 것은 FT를 각각에 대응해서 수행하는 것을 의미하며, 이는 frequency space 상에서 서로 다른 band-width를 커버하게 된다. 이렇게 band-pass filter의 scale parameter를 단순히 바꾸기만 하더라도 location 또한 달라지게 된다. 그리고 여기서 반드시 알아야하는 부분으로 band-pass filter를 보면 원점에서 시작하게 된다. 그렇기 때문에 band-pass filter는 frequency component가 0인 부분은 커버할 수 없게 된다. 그래서 우리는 추가로 filter 1개를 도입시켜 이 부분을 커버할 수 있다. Scalining function으로 불리는 low-pass filter 1개를 통해서 frequency space 상에서 frequency가 0인 부분을 포착하게 된다. 사실 scalining function $\phi$는 band-pass filter와 다르게 추가적인 부분으로 사용하는 사람이 선택을 할 수 있는 부분이다. Wavelet을 어떻게 선택하는지에 따라 scaling function을 가져야하는지가 결정될 수 있지만, mother wavelet의 경우에는 transformation의 기반이 되는 basis로서 항상 존재해야 한다.

이제 WT의 기반이 되는 wavelet에 대해서 어느정도 알아보았으므로, 이제는 WT가 어떻게 동작되는지 수식적으로 알아보자. Signal $f(x)$에 WT를 적용하는 것은 FT와 마찬가지로 inner product를 수행하게 된다. $f(x)$가 주어졌을 때 우리는 추가로 미리 정의했거나 선택한 mother wavelet $\psi$를 사용해서 이들간 inner product를 통해서 WT를 수행하고 wavelet coefficient $W_f(s,a)$를 얻을 수 있다. FT에서는 Fourier coefficient를 얻었지만, WT에서는 이와 마찬가지로 wavelet coefficient를 얻게되는 것이다. $\psi$에는 기본적으로 2개의 scalining과 translation parameter를 가지고 있기 때문에 $W_f(s,a)$에도 2개의 variable $s,a$를 가지게 된다. 따라서 $W_f(s,a)$는 결국 scalining variable $s$와 translation variable $a$에 의해서 결정이 될 것이다.

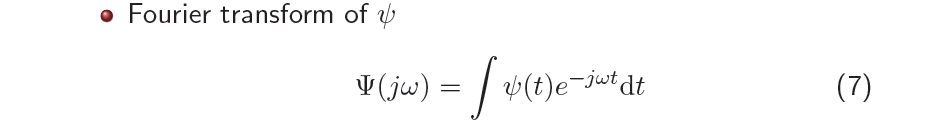FT의 수식을 보면 basis로 $e^{j\omega t}$의 conjugate를 사용하여 signal과 곱한뒤 summation을 취하는 식으로 동작한다. 우리는 mother wavelet $\psi$에 FT를 수행하고 싶고, 이는 wavelet basis의 basis를 바꾸는 것과 같다.

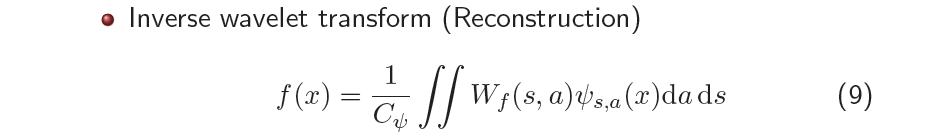우리는 wavelet coefficient $W_f(s,a)$를 얻게되면 이를 이용해서 inverse transformation 또한 정의할 수 있어야 한다. Inverse wavelet transformation (IWT)는 IFT와 마찬가지로 coefficient과 basis를 곱한뒤 2개의 integral을 취하게 된다. 여기서 integral이 2개인 이유는 coefficient가 2개의 parameter가 $s$와 $a$를 가지기 때문이다. 그래서 integral을 할 때 전체 $s$와 전체 $a$에 걸쳐서 marginalization을 해줘야 한다. 이렇게 IWT를 통해서 원래의 signal $f(x)$를 reconstruction할 수 있다.

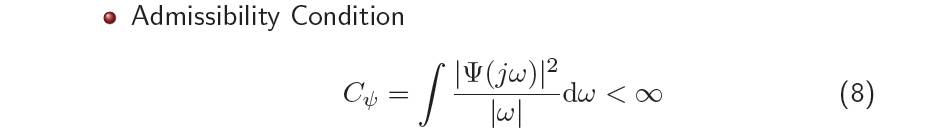이제 중요한 것은 그렇다면 항상 IWT를 정의할 수 있는지이다. 정답은 No이다. 이를 설명하기 위해서 IFT을 다시 생각해볼 필요가 있다. IFT에는 scalining factor로 $1/2\pi$가 존재한다. 여기서 $2\pi$는 complex sinusoidal signal의 property로부터 비롯된 값이다. 즉, $2\pi$라는 값은 transformation하고자 하는 basis로부터 계산이 된 결과이다. IWT에도 scaling factor가존재하며, 우리는 이를 $C_\psi$로 notation하여 basis로부터 얻고자하며, 이는 위와 같이 Admissibility condition을 만족하여 구해지게 된다. Frequency space 상에서 우리가 사용하는 basis의 power가 finite해야한다는 것이 Admissibility condition이다. 우리는 이러한 조건에서만 IWT을 정의할 수 있다. $C_\psi$가 infinity로 발산한다고 생각해보면, 즉, mother wavelet에 FT을 취하여 얻어진 basis $\Psi$의 power가 값이 infinity로 커지게 되면 IWT에서 우변의 값이 항상 0으로 수렴하게 되어 IWT가 제대로 정의되지 못할 것이다. 그렇기 때문에 $C_\psi$는 항상 infinity보다는 작아야 우리가 transformation에 사용하고자하는 basis로부터 frequency space에서 이들의 power가 summable하게 되는 것이고, 우리는 이러한 조건을 Admissibility condition이라고 한다. 요약하자면 Admissibility condition을 만족해야만 IWT를 정의할 수 있게 된다. 그리고 IWT를 $f(x)$의 reconstruction이라고 표현하기도 한다.

Scale and Translation of CWT

지금부터는 이러한 WT가 convolution이 되는 과정을 설명하고자 한다. 먼저 WT를 $T^s$라는 operator로 정의해보자. 어려워보이지만 우리는 operator $T^s$를 $f(a)$에 곱했을 때 wavelet coefficient $W_f(s,a)$를 얻게 될 것이다. 즉, $T^s$는 signal을 wavelet cofficient로 mapping해주는 operator인 것이다.

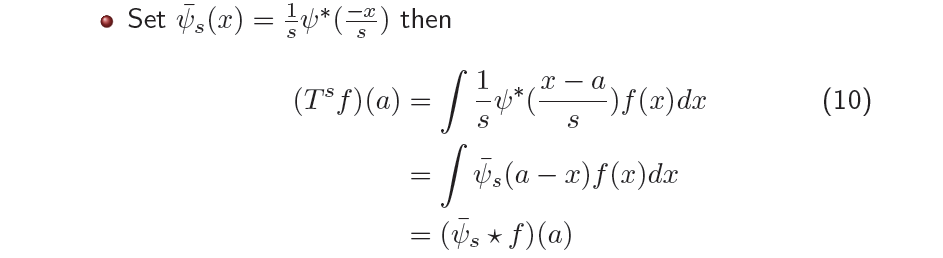다음으로 mother wavelet $\psi_{s,a}(x)=\frac{1}{s}\psi(\frac{x-a}{s})$에서부터 parameter $a$를 날려서 간단하게 $\bar {\psi}_s(x)=\frac{1}{s}\psi^*(\frac{-x}{s})$를 정의할 수 있을 것이다. 원래 $\psi_{s,a}(x)$는 $x$에 대한 function이지만 또한 $a$에 대한 function으로 생각해볼 수 있어서 위와 같이 $T^s$를 $f(a)$에 적용한 $(T^sf)(a)$를 구할 수 있을 것이다. 이것이 괜찮은 이유는 나와 상대방 사이의 거리나 상대방과 나 사이의 거리가 동일하기 때문이다. 관점의 차이일 뿐 결과에는 차이가 없을 것이다.

$T^sf(x)$는 결국 wavelet coefficient $W(s,a)$이고, 이는 $\int\frac{1}{s}\psi^* (\frac{x-a}{s})f(x)dx$로 구해질 수 있다. 우리는 여기서 basis를 $x$에 대한 function 혹은 $a$에 대한 function 둘다로 고려할 수 있다. 그러면 우리는 이제 $T^sf(a)$를 구할 수 있고, 이는 마찬가지로 $W(s,a)$가 되면서 $\int\frac{1}{s}\psi^* (\frac{x-a}{s})f(x)dx$가 $\int\bar\psi_s(a-x)f(x)dx$와 같이 계산되어 진다. 여기서 중요한 것은 wavelet 부분이 우리가 정의한 새로운 wavelet $\bar\psi_s$로 대체가 된 것이다. 간단하게 $x$ 대신에 $a-x$를 넣으면 위와 같은 결과가 도출될 것이다. 그리고 식을 자세히 보면 굉장히 익숙한 convolution 형태의 식으로 만들어진 것을 볼 수 있다. 이는 결국 $f(x)$와 $\bar\psi_s(x)$ 사이의 convolution으로 해석이 된 것이고, 따라서 우리는 WT가 convolution임을 이렇게 증명해온 것이다. WT가 convolution이 될 수 있음을 간단하게 basis의 변경을 통해서 유도하였다. 정확히 이야기하면 여전히 동일한 basis $\psi$를 사용하지만 간단하게 식을 재정의해서 얻어진 $\bar \psi$를 통해서 WT가 convolution임을 설명할 수 있다. 알아야할건 $x$에 걸쳐서 integration을 해서 결국 parameter $a$를 갖게된 것이다.

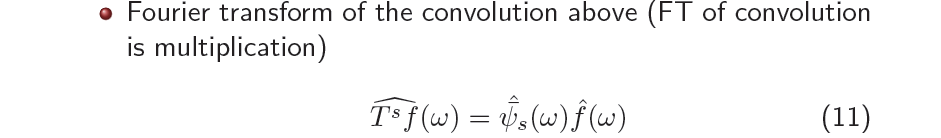그렇다면 우리가 이러한 것들을 왜 했을까? 우리가 결국 하고자 하는 것은 위의 operation에 FT을 취하는 것이다. 중요한 성질 중 하나로 time space에서 convolution은 frequency space에서 multiplication이다. 이는 잊어서는 안되는 정말 중요한 내용이다. Time space에서 mother wavelet과 signal의 convolution을 FT를 통해서 frequency space로 보내면 filter에 해당하는 mother wavelet과 Fourier coefficient에 해당하는 signal의 multiplication으로 표현이 된다. $a$와 $x$의 space 상에서의 convolution이 frequency space에서 multiplication이 되는 것은 위의 식을 통해서 확인할 수 있다.

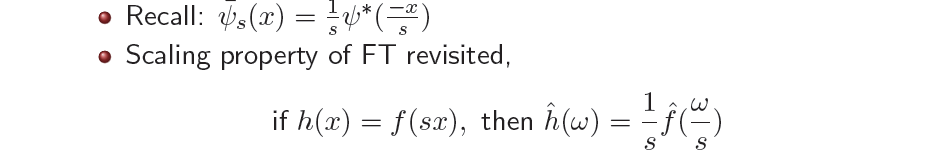이러한 내용은 지금부터 알아가는 내용을 위해서 중요한 역할을 한다. 다시 FT의 scalining property를 생각해보자. Time space에서 scale $s$가 FT를 통해서 frequency space로 가면 기존과 반대로 동작했었다.

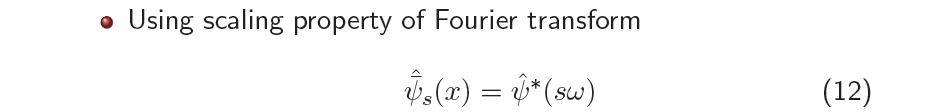이러한 FT의 scalining property를 사용해서 우리는 위와 같은 수식을 논할 수 있게 된다. $\hat{\bar\psi_s}(\omega)$가 $\hat\psi^*(s\omega)$로 대체될 수 있다. 어떻게 이러한 식이 가능한 것일까? 우리는 $\bar\psi_s(x)=\frac{1}{s}\psi^*(\frac{-x}{s})$로 정할 수 있음을 앞에서 확인했었다. 우리는 양변에 FT를 취하게 되면 좌변은 $\hat{\bar\psi_s}(\omega)$가 되며, 우변은 $\frac{1}{s}\hat{\psi}^*(\frac{-\omega}{s})$가 될 것이다. 다시 이 우변을 scalining property를 통해서 정리하면 $\hat{\psi^*}(s\omega)$가 될 것이다. 결국 위와 같은 식이 성립하게 되는 것이다.

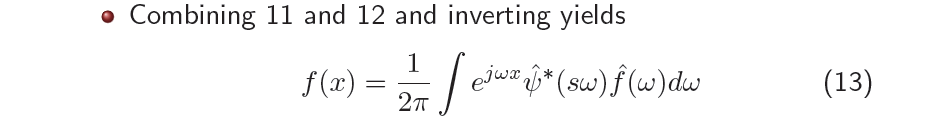마지막으로 식 11과 12를 종합해보면, 우리는 먼저 $T^sf(a)=f(x)*\psi_{s,a}(x)$로부터 FT을 통해서 $\widehat{T^sf}(\omega)=\hat f(\omega)\hat{\bar \psi_s}(\omega)$와 같이 frequency space에서 multiplication으로 구해지는 것을 확인하고, 이제 $\hat{\bar \psi_s}(\omega)$을 $\hat{\psi_s^*}(s\omega)$로 대체할 수 있게 되었다. 결과적으로 $\widehat{T^sf}(\omega)=\hat f(\omega)\hat{\psi_s^*}(s\omega)$에서 $\hat f(\omega)$은 Fourier coefficient가 되고 $\hat{\psi_s^*}(s\omega)$은 frequency space에서 band-pass filter의 역할을 하는 wavelet $\psi$에 의해 결정된 band-pass filter function의 역할을 하게 될 것이다. 즉, frequency space에서 특정 frequency component들을 wavelet basis로부터 주어진 filter function으로 filtering하는 과정으로 이해할 수 있다.
지금까지 우리는 WT의 과정을 convolution으로 증명하였고, 여기에 FT를 수행해서 wavelet basis로부터 filter를 구해 filtering하는 과정까지 흐름이 이어져오고 있다. 이제 FT를 이미 적용했기 때문에 여기에 다시 IFT를 적용할 수 있을 것이다. IFT는 Fourier coefficient과 Fourier basis를 곱해주기 때문에 우리는 앞서 구해진 WT의 결과에 FT를 수행한 $\hat f(\omega)\hat{\psi_s^*}(s\omega)$을 coefficient로 간주해서 Fourier basis $e^{j\omega x}$를 곱하고 integral을 취해서 위와같은 filtering을 수행한 reconstructed signal $f(x)$를 만들 수 있다. 전체적으로 식 13은 IFT의 형태를 보이고 있다. 하지만 중요한 점은 기존의 IFT와는 다르게 $\hat f(\omega)$를 wavelet basis를 이용해서 filtering을 했다는 것이다. $f(x)$가 완벽하게 복원되었다고 이야기하기는 어렵다. 다만, 원하는대로 filtering된 결과의 reconstruction이라는 의미가 존재한다.

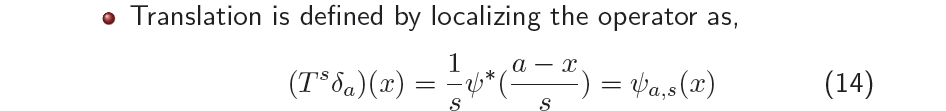우리가 계속해서 사용하는 wavelet basis $\psi_{a,s}(x)$는 delta function $\delta$에 wavelet operation을 수행하여 얻은 것과 같다. $\delta$에 FT를 적용하게 되면 1이라는 사실은 알아두면 좋다. Time space 상에서 $\delta$ function은 frequency space 상에서는 constant function으로 그 값이 전부 1이 된다. 이것이 의미하는 것은 Fourier coefficient $\hat f(\omega)$ 자체가 1이 되는 것이고, 결과적으로는 wavelet basis를 IFT를 통해서 reconstruction하는 것과 같아지게 된다. 그래서 mother wavelet을 delta signal의 WT으로 이해하면 된다.

Summary

정리를 해보면 우리는 FT부터 WT까지 그 흐름을 이어오면서 알아보았다. 먼저, FT는 basis로 $e^{j\omega t}$를 사용하고 이는 infinite support라는 특징이 있다. WT는 새로운 basis로 mother wavelet $\psi_{s,a}(x)$를 사용하고 이는 finite support라는 대조되는 특징이 있다. 우리는 origianl signal $f(x)$와 2개의 parameter를 지닌 $\psi_{s,a}(x)$간 inner product와 integration을 통해서 WT를 수행하고 wavelet coefficient $W_f(s,a)$를 얻을 수 있다. IWT 또한 wavelet coefficient과 wavelet의 inner product와 integration을 통해서 $f(x)$를 구성할 수 있었다. 여기에는 basis로부터 나온 Admissibility condition이 존재하며, 이는 $C_\psi$가 frequency space 상에서 finite power를 보이기만 한다면 우리는 IWT를 정의할 수 있게 된다. 모든 흐름이 직관적이고 간단해 보일 수 있지만, 가장 중요한 핵심으로는 이러한 WT이 "band-pass filtering"으로 설명될 수 있다는 점이다. 그리고 WT은 Fourier coefficient가 있을 때 여기에 mother wavelet에 따라 결정되는 filtering을 적용하는 과정으로 볼 수 있다. 여기에는 convolution이 frequency space에서 multiplication으로 동작한다는 성질이 중요하게 작용한다. WT는 또한 finite support이기에 FT의 큰 문제 중 하나인 ringing artifact가 없다는 장점도 존재한다.