[기계학습] Linear Regression - Ridge Regression

Overfitting Issue and Regularization

LS method는 MLE를 연결시켜서 생각해볼 수 있었고, density estimation에서 MAP를 이야기했을 때 등장했던 prior의 관점을 이번에는 linear regression에 접목해서 생각해보려고 한다. 만약 prior이라 해서 사전지식이 $w$에 있게 된다면 어떻게 될까라는 생각을 해볼 수가 있고, 이러한 관점은 sample의 수가 제한적일 때 매우 유용하며 이번에는 이와 관련하여 overfitting issue와 왜 regularization이 필요한지에 대한 그 동기를 살펴보고자 한다.

Overfitting

Observation의 수보다 parmeter의 수가 많을 때 보통 overfitting issue가 어디서든 발생하곤 한다.
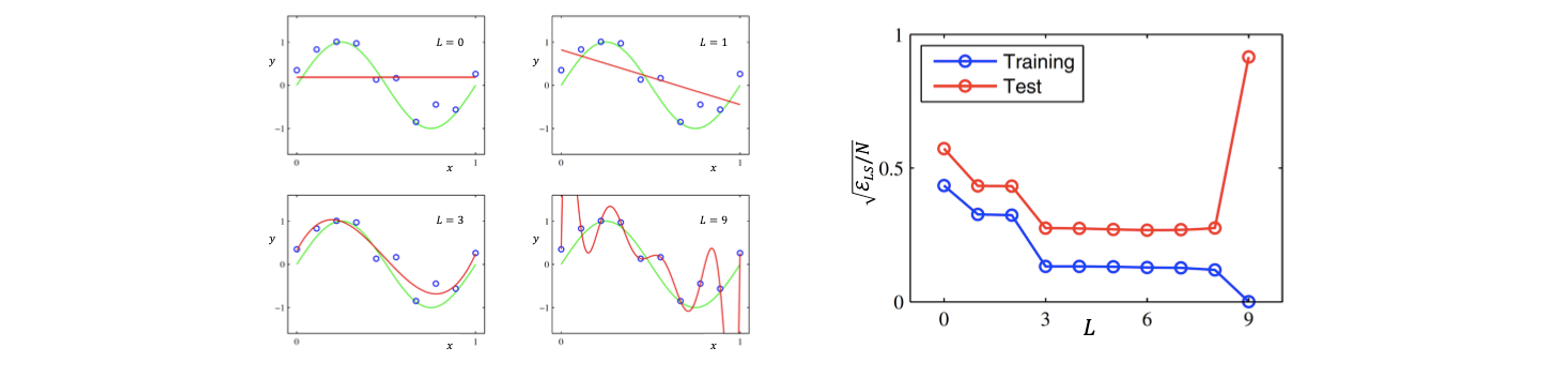Polynomial regression에서 feature의 개수인 $L$이 매우 작은 경우에는 보통 underfitting이 발생하게 된다. Underfitting issue는 우리의 예측 model인 빨간선이 우리의 observation인 data로부터 멀리 떨어진 경우를 말한다. $L$이 증가함에 따라서 underfitting issue는 줄어들게 되어 true model에 가까운 결과를 보여주지면 만약 $L$이 매우 커지게 되면 least square은 0이 되어 우리가 관찰한 data에는 모두 만족하게 되지만, 이는 true model과는 거리가 멀어져 새로운 data에 취약해지게 된다. 이러한 현상을 overfitting이라고 하고 training 성능은 정말로 만족스럽지만, 정작 중요한 test 성능은 많이 떨어지게 된다.

Regularization

그래서 machine learning을 연구하는 사람들은 이러한 overfitting issue를 줄이기 위해서 prior을 수식에 추가해서 이를 방지하고자 했다. 사람들은 실험을 통해서 overfitting issue가 발생했을 때 parameter의 절대값이 매우 커지는 현상을 관찰할 수 있었다.
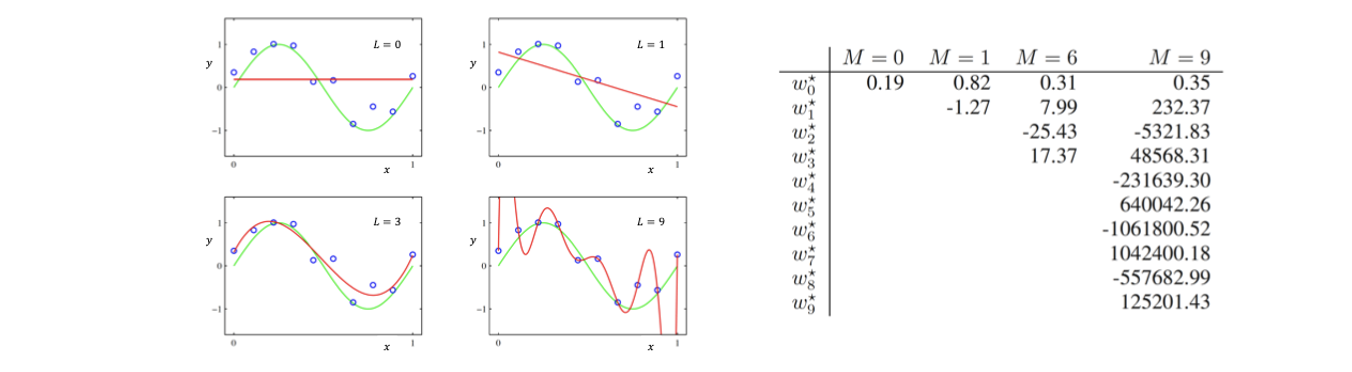이것이 의미하는 것은 우리의 model이 예측한 결과가 input data에 매우 민감하다는 것을 나타낸다. 만약 input $x$를 조금 바꾸었음에도 매우 큰 값을 가지게 된다면 우리의 예측을 매우 빠르게 변화시킬 것이다. 이러한 현상은 아무도 원하지 않을 것이고, 대부분 연속적인 구조를 원하게 될 것이다. 여기서 연속적이라는 것은 비슷한 input에 대해서는 비슷한 output을 원한다는 것이다. 비슷한 input임에도 완전히 다른 output을 가진다는 것은 model을 통해서 어떠한 설명도 제공해줄 수 없는 것과 같다. 이러한 overfitting issue를 막기 위해서 디자인된 것이 regression task에 대해서 다음과 같은 새로운 loss function이다.

기존의 fitting error는 least square error로 최소로 만들어야 하는 것은 동일하다. 여기서 regularizer라는 하나의 항이 추가되었고, 이는 parameter의 크기를 증가시키는 민감한 solution을 원하지 않고 모든 parameter가 작아지기를 원한다는 믿음이 반영된 항이다. 그래서 이 식에서는 $\lambda$를 이용해서 fitting error와 우리의 믿음을 반영한 regularizer 사이를 조절할 수가 있다.

이러한 loss function을 ridge regression이라고 하고, ridge regression은 LS method의 경우와 마찬가지로 수학적으로 closed form solution을 가질 수가 있다. Ridge regression을 parameter $w$에 관하여 derivative를 구하고 0으로 두어 최소가 되는 stationay point를 찾게 되면 이 지점에서의 $w$가 우리가 원하는 최적의 parameter가 되는 것이다.

이렇게 얻은 결과는 $w_\text{LS}=(\Phi^T\Phi)^{-1}\Phi^Ty$와 매우 유사한 형태를 가지고 있고, 다만 차이점으로 $\lambda$에 의한 항이 추가되었다는 것이다. 여기서 $\lambda$가 매우 작아지면 LS method와 ridge regression이 같아지게 된다. $\lambda=0$이 되어 log 값이 음의 무한대가 된다면 overfitting이 일어나는 것이다. 반대로 $\lambda$가 증가하게 되면 LS method와는 완전히 달라지게 되고 보통 1이라고 설정하게 되면 log 값은 0이 되어 underfitting 현상을 발생하게 된다. 따라서 $\lambda$ 값을 잘 선택해주는 것이 정말로 중요하다.

Interpretation of Ridge Regression: MAP

Overfitting issue를 막기 위한 방안으로 ridge regression을 알아보았고, machine learning을 연구하던 사람들은 ridge regression solution을 확률적으로 접근하기를 원했다. 확률하면 대표적인 예시로 동전 던지기를 생각했을 때 우리의 머리 속에는 일반적으로 앞면이 나올 확률을 0.5라고 믿고 있다. 이처럼 우리는 형식적으로 우리의 믿음을 정량화하고 싶다는 생각이 있으며, 이러한 관점을 ridge regression과 함께 생각해보고자 했던 것이다. 최적의 $\lambda$ 값을 잘 설정하는 것이 중요한 것은 사실인데 실질적으로 훌륭한 $\lambda$에 대한 이해와 해석이 부족한 상태였다. 그래서 MAP의 관점에서 ridge regression을 해석하고 이해하다보면 $\lambda$를 선택하는데 도움이 될 것이라는 이야기이다.

이전에 LS method에서 likelihood model을 설정했을 때 평균이 0인 additive Gaussian noise를 가정했었다. 이번에는 MAP를 위해서 parameter $w$에 대한 확률을 평균이 0인 Gaussian prior distribtuion으로 가정하고자 한다. 경험적으로 우리는 실험을 통해서도 봤지만 parameter $w$의 절대값을 최소한으로 줄이고 싶다. 이를 확률적으로 정의하고자 하려면 0을 중심으로 distribtuion들이 존재하면 된다. 우리의 이러한 믿음을 표현하는 방법은 다음과 같은 평균이 0인 Gaussian distribution으로 prior을 만들면 된다.

그리고 likelihood model은 LS method 때와 같이 가정하면 된다. Model이 $y=\Phi w+\varepsilon$이라고 했을 때 마찬가지로 noise $\varepsilon$이 $\mathcal{N}(0,\sigma^2I)$를 따르면 된다. 그러면 $y$에 대한 평균은 noise가 0이라 그냥 $\Phi w$가 될 것이고 variance는 동일할 것이다.

이로부터 posterior distribtuion은 다음과 같다.

Gaussian identities로부터 posterior 또한 여전히 Gaussian distribtuion이고 MAP를 통해서 해를 구하면 다음과 같아지게 된다.

만약 우리의 믿음인 prior distribtuion에서 variance $\Sigma$가 $\frac{\sigma^2}{\lambda}I$와 같아지게 되면 다음과 같이 MAP solution과 ridge regression solution이 같아지게 된다.

결론적으로 훌륭한 parameter일수록 그 크기가 작다는 이러한 믿음을 기반으로 prior distribtuion을 통해서 posterior를 구하게 되었을 때 이를 최대로 만드는 최적의 parameter $w_\text{MAP}$을 구할 수 있었고, 여기서 prior distribtuion의 variance $\Sigma$를 설정해주는 것에 따라서 ridge regression과 MAP를 동일하게 만들 수가 있다. 이렇게 ridge regression을 확률적으로 어떻게 접근하는지 알아보았다.