[기계학습] Linear Regression - Non-Linear Regression

JAEYOON SIM·2021년 9월 22일

Machine Learning

목록 보기

11/35

Non-Linear Regression

지금까지는 regressor task에 대한 기본적인 model에 대해서 알아보았다. 특히 linear regression을 보면서 LS method와 MLE를 연결시켜 보았으며 이때의 noise는 평균이 0인 additive Gaussian noise라는 가정이 들어가 있었다. 하지만 MLE의 경우 overfitting issue로 한계가 있었고, 이를 해결하기 위해서 regularization에 대해서 알아보았다. 특히 ridge regression에 대해서 보았으며, 이때 objective function은 parameter에 대한 L2-normd으로 표현되었다. 이번에는 이러한 ridge regression을 Gaussian prior과 함께 MAP와 연결시켜 보았다. 각 problem에 대해서 closed form solution이 존재했으며, data point들이 주어지게 되면 정확하게 각각의 optimization에 대한 optimal solution을 구할 수 있었다.

그러나 현실에서는 이러한 방법들이 사실상 가능성이 그리 크지 않으며, 특히 closed form solution이 non-trivial한 경우에 대해서 non-linear regression에 대해서 알아보고자 한다.

Learning as Continuous Optimization

가장 먼저 regression task를 풀기 위해서 문제를 정의하고자 한다. 우리는 지금까지 알고있지 않은 parameter를 통해서 model을 정의해왔다. 여기서 model은 regression task에서는 observation $x$ 에 대한 output $y$ 의 conditional expecation에 근사하도록 정의했었다.

f(x) \simeq \mathbb{E}[y|x]

여기서 model $f(x)$ 는 parameter $\theta$ 에 의해서 매개변수화 되었고, 우리는 최적의 $\theta$ 를 찾기를 원한다. 대부분의 parameter estimation problem은 continuous optimization problem으로 수식화 될 수 있으며, 우리의 목적은 loss 혹은 risk function을 최소로 만드는 parameter $\theta$ 를 찾는 것이다.

\operatorname*{arg\,min}_\theta L(\theta) = \operatorname*{arg\,min}_\theta \sum_{i=1}^N l(y_i,f(x_i,\theta))

LS method라면 loss function $L(\theta)$ 은 $||y_i-f(x_i,\theta)||^2$ 와 같은 squared error로 정의되었을 것이다. 이처럼 우리는 항상 regression task에 대응하는 continuous optimization problem을 찾을 수가 있다.

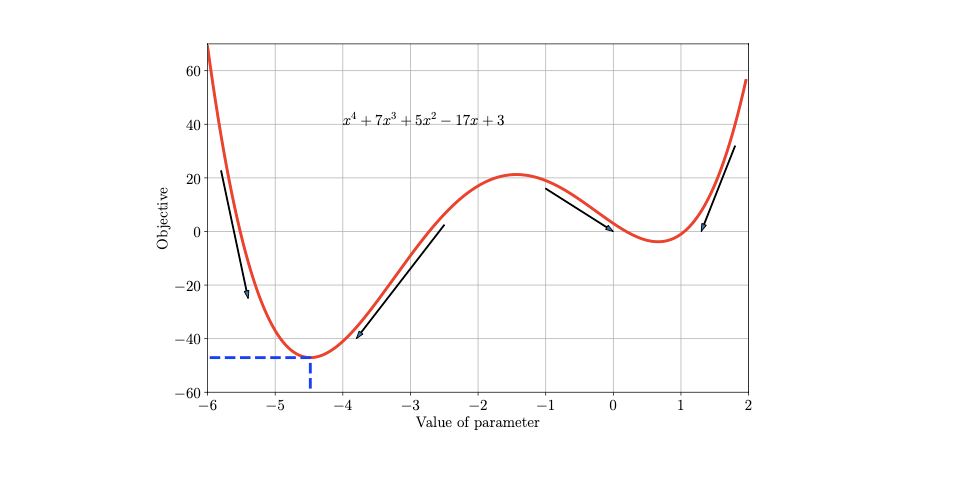예를 들어서 loss function이 다음과 같이 주어졌을 때, optimization은 이 값을 최소로 만들고자 하는 $\theta$ 를 찾으려고 할 것이다.

L(\theta)=\sum_{i=1}^N l(y_i,f(x_i,\theta))=\theta^4+7\theta^3+5\theta^2-17\theta+3

만약 convex function을 가지고 있다면, 이러한 minimization problem같은 경우는 간단하게 stationay point를 찾음으로써 해결할 수 있을 것이다. Stationay point는 derivative를 구해서 0으로 설정한 지점의 값이 된다.

\frac{dL(\theta)}{d\theta}=0

Limitations

사실 이러한 경우는 매우 운이 좋은 경우이다. 현실에서 대부분의 model들 같은 경우에는 closed form solution을 구하는 것이 불가능한 형태로 되어 있다. 때때로 loss function은 parameter에 대해서 convexity를 보장받지 못할 것이고, 이러한 경우에는 stationay point가 minimization point라고 단정지을 수가 없다.

또한 대부분의 경우에 derivative를 구하는 것 자체만으로도 intractable할 수 있다. Abel-Ruffini theorem(근의 공식)은 polynomial equation에서 차수가 5만 넘어가도 대수적인 해가 없다고 이야기하고 있다. 이러한 것은 derivative를 구하는데 어려움이 존재한다는 하나의 예시로 볼 수 있다. 그렇다면 어떻게해서 문제를 해결해야 하는 것일까?

Gradient Method

Gradient Descent(GD)

Optimization problem을 쉽게 구할 수가 없을 때 사용할 수 있는 방법으로 gradient method가 있다. 특히, minimization problem에 대해서는 gradient descent(GD)를 사용할 수가 있다. 그렇다면 어떻게 접근을 하는지 하나씩 살펴보도록 하자. 먼저 우리가 풀고자 하는 objective function $L$ 이 다음과 같이 주어졌다고 할 것이다.

L:\mathbb{R}^n\rightarrow \mathbb{R}

우리는 $L$ 이 미분이 가능하다고 가정할 것이지만, 이전처럼 쉽게 closed form solution을 찾을 수 없다고 할 것이다. 그래서 GD는 식 전체를 이용해서 derivative를 구하는 것이 아닌 특정 지점에 대해서 derivative를 구할 수 있다는 가정으로 시작할 것이다. 그래서 이 minimization problem에서 objective function을 최소로 만들기 위해서 먼저 initial point $x_0$ 로부터 다음과 같이 업데이트 과정을 진행해주고자 한다. 이때 $x$ 는 parameter이다.

x_1=x_0-\gamma(\underbrace{(\nabla L)(x_0)}_{\text{Derivative at }x_0})^T

Parameter는 반복해서 업데이트가 될 것이고, 각각의 반복에서는 이전의 parameter로부터 해당 parameter의 derivative를 구한 뒤 step-size $\gamma$ 를 곱해서 빼주는 식으로 업데이트가 될 것이다. 이렇게 매 반복마다 업데이트가 되며 이를 정리해서 일반화 시키면 다음과 같이 간단한 GD algorithm을 만들 수가 있다.

x_{t+1}=x_t-\gamma_t(\underbrace{(\nabla L)(x_t)}_{\text{Derivative at }x_0})^T

다음은 이를 그래프를 통해서 해석한 것이다.
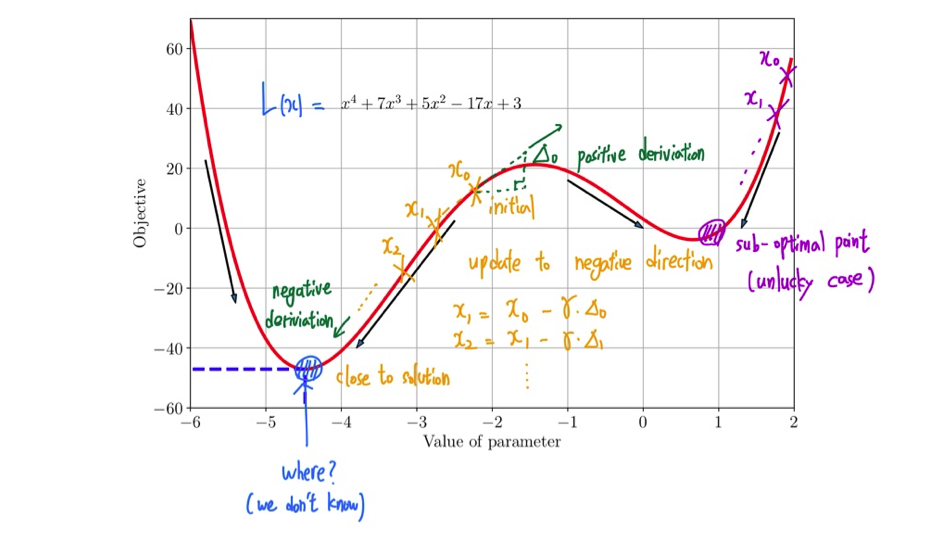주황색과 같이 초기의 point가 잘 위치하게 되면 GD method에 따라 한단계씩 업데이트를 시키면서 최적의 지점을 찾아가게 될 것이다. 다만 보라색과 같이 초기값을 잘못 설정해주게 되면 local minimum에 빠지게 되는 문제점도 존재하게 된다. 결국 이 그래프를 통해 GD method를 살펴보게 되면 한번에 closed form solution을 구하지는 못하지만 이렇게 매 단계마다 업데이트를 시키면서 결국에는 optimal solution을 찾을 수 있다는 것을 확인할 수 있고, 이러한 접근 방식은 매우 휴리스틱하기 때문에 local minimum과 같은 잘못된 지점에 도달하기도 한다.

위의 예시는 parameter가 1개일 때의 예시이고, 이번에는 parameter가 2개인 예시를 보도록 하자. 여기서는 2개의 parameter $x_1,x_2$ 를 동시에 optimization해야 한다. 다음과 같이 loss function의 graphical illustration이 있다고 할 것이다.
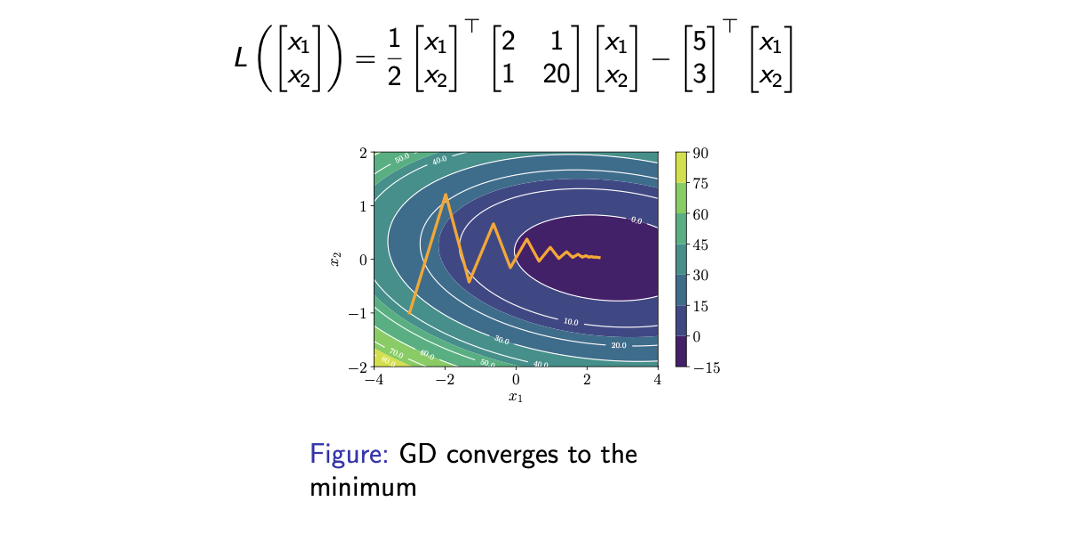각각의 contour는 2개의 parameter 쌍에 대한 loss function의 값을 나타내고 있다. 시작 지점을 (-3,-1)이라고 했을 때 GD method를 사용함에 따라 업데이트가 될 때마다 loss 값이 줄어들어드는 것을 확인할 수 있다.

Stepsize

만약 convex objective function이 있고 minimization problem을 풀어야 할 때 optimal point에 대한 convergence를 보장받을 필요가 있다. 그러나 대부분의 model은 non-convex loss function을 가지게 되어 GD가 항상 optimal point에 대한 convergence를 보장할 수 없게 된다. 그래도 만약 조심스럽게 GD를 디자인하게 된다면, 물론 대부분의 경우에서는 발산하겠지만 적어도 하나의 point에 대한 convergence를 가질 수 있을 것이다. 다음의 예시를 통해서 GD의 divergence를 알아볼 것이다.
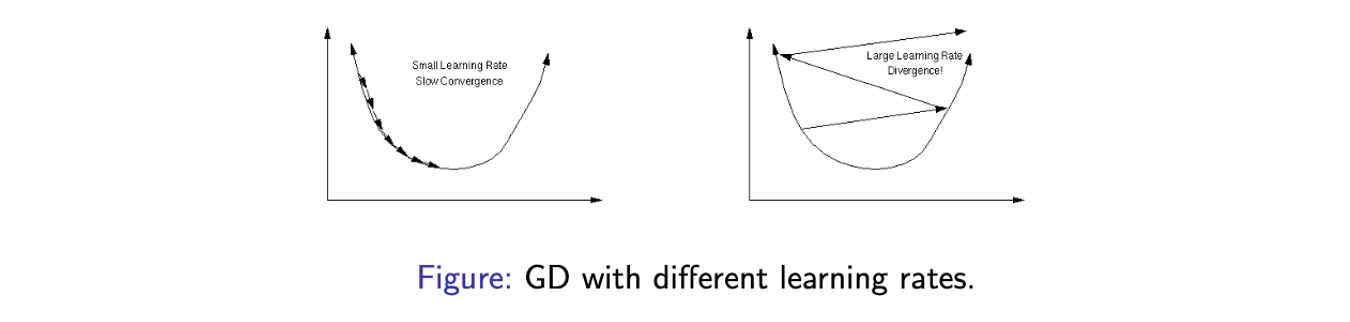예를 들어 minimization problem을 하나의 parameter에 대해서 풀고자 할 때, 위의 그래프에서 y축은 loss 값이 되고 U 모양을 가지게 되어 minimum point를 찾을 수가 있다고 해보자. 이 그래프에서 optimal point를 찾을 수 있는 방법은 오로지 step-size를 잘 설정했을 경우이다. 좌측은 step-size, 즉 learning rate를 작게 설정해서 천천히 convergence를 보장할 수 있게 된다. 반대로 만약 우측과 같이 learning rate를 너무 크게 설정하게 되면 매우 큰 값이 곱해지기 때문에 optimal point를 찾지 못하고 발산하게 된다. 이러한 현상을 overshoot이라 하고 결국에 step-size를 잘 설정하는 것이 GD에 있어서 가장 중요한 부분인 셈이다.

그렇다면 step-size를 잘 설정하기 위해서는 어떻게 해야할까? 휴리스틱한 방법을 통해서 step-size를 잘 찾는 방법에 대해서 알아보고자 한다. 만약 funtion 값이 gradient step 이후에 증가하게 되었다면, 이는 step-size가 너무 크게 설정되었다는 뜻이기에 이러한 경우에는 gradient step을 멈추고 step-size를 줄여야 한다. 이번에는 반대로 function 값이 감소하게 된다면 이번에는 step-size를 증가시켜주면 된다. 이러한 방법은 loss function이 증가하는지 혹은 감소하는지에 따라 수동적으로 step-size를 변경시켜줘야 하기에 그리 좋은 방법은 아니다. 그리고 이러한 접근은 몇가지 경우에 대해서 그리 좋지 못할 것이다. 특정 objective function에 대해서는 너무 많은 시간이 소모될 수도 있다.

1. Momentum

이러한 한계가 존재하기 때문에 좀 더 개선된 방안이 필요하고 그 방법 중 하나가 momentum이다. Momentum이라는 단어는 물리학으로부터 등장하게 된 단어이다. 운동량이라고 불리는 momentum은 gradient update 시에 추가정인 항을 통해서 이전의 상황을 기억하고 위에서 2개의 parameter를 optimization 할 때 진동하던 문제에서 진동을 최대한 줄여서 하나의 축을 따라 optimal point로 갈 수 있도록 도와주는 역할을 한다. Momentum은 다음과 같이 2개의 식으로 설명이 가능하다.

x_{i+1}=x_i-\gamma((\nabla f)(x_i))^T + \alpha\Delta x_i \qquad \alpha\in[0,1]

\Delta x_i=x_i - x_{i-1} = \alpha\Delta x_{i-1}-\gamma_{i-1}((\nabla f)(x_{i-1}))^T

첫번째 식은 parameter를 바로 업데이트 하게 되며 첫번째 항은 GD와 똑같지만 두번째 항은 추가적인 항으로 momentum을 나타내고 있다. $\Delta x_i$ 는 두번째 식에서 정의하고 있다. 현재 parameter와 이전의 parameter 사이의 차이로 정의를 하게 되면 momentum을 사용한 GD는 이전의 업데이트를 기억해서 진동을 최대한 줄이게 된다. 현재와 이전의 gradient를 linear combination을 한 것과 같이 업데이트가 되기 때문에 한쪽 방향으로 크게 튀는 것을 막으면서 업데이트를 진행시킬 수 있다.

2. Stochastic Gradient Descent(SGD)

Momentum은 hyper parameter의 선택에 있어서 overshooting을 막는데 도움을 주는 하나의 방법이었다. Objective를 구하거나 derivative를 계산하는데 대부분 많은 양의 연산이 필요하게 된다. 단순히 loss function을 구하는데에도 많은 양의 계산이 필요하고 같은 data에 대해서 derivative를 구하는데도 반복적인 계산이 필요하게 된다. 이러한 계산은 현실에서는 불필요하게 많아서 사람들은 일부분만 sampling 해서 구하고 근사시키자는 방법을 생각했다. 이를 GD에서의 mini-batch라고 부르고 다른 말로는 stochastic gradient descent(SGD)라고 한다.

Data의 양이 너무 많아서 시간이 오래 걸릴 것 같으면 사용하는 방식으로 data 전부를 이용해서 GD를 구하는 것이 아니라 어떻게든 data를 sub-sampling을 해서 근사시키고자 하는 것이다.

\frac{dL(\theta)}{d\theta} \simeq \sum_{i\in\mathcal{B}}\frac{dL_i(\theta)}{d\theta}

|\mathcal{B}| << N

Noisy Gradient

Mini-batch를 보통은 무작위로 선택하기 때문에 이러한 mini-batch를 사용하는 방식을 noisy gradient라 부른다. 만약 data point를 일부분만 사용해서 gradient를 구하게 되면 다음과 같을 것이다.

\frac{dL_\mathcal{B}(\theta)}{d\theta} = \sum_{i:x_i\in\mathcal{B}}\frac{dL_i(\theta)}{d\theta}

\text{where }\mathcal{B} \text{ is a subset of data } \mathcal{D}=\{(x_1,y_1),\dots,(x_N,y_N)\}

GD의 경우 data distribution $p(x,y)$ 에 대한 gradient expectation이기 때문에 나름 이렇게 사용하는 것이 타당하게 된다. 마찬가지로 SGD 또한 data distribtuion에 대한 gradient expectation으로, 만약 sub-sampling을 할 때 uniform random smapling을 사용한다면 우리는 쉽게 gradient의 expected value를 확인할 수 있을 것이다.

\mathbb{E}\bigg[\frac{dL(\theta)}{d\theta}\bigg]=\mathbb{E}\bigg[\sum_{i=1}^N \frac{dL_i(\theta)}{d\theta}\bigg]

=N\mathbb{E}\bigg[\frac{1}{|\mathcal{B}|} \sum_{i:x_i\in\mathcal{B}}\frac{dL_i(\theta)}{d\theta}\bigg]=\frac{N}{\mathcal{B}}\mathbb{E}\bigg[\sum_{i:x_i\in\mathcal{B}}\frac{dL_i(\theta)}{d\theta}\bigg]

이러한 과정을 통해서 GD에서의 gradient와 SGD에서의 gradient를 수식으로 연결시켜 볼 수 있다. 마지막 expectation 앞에 붙은 ratio는 중요하며, 이는 우리가 batch의 크기와 step-size를 바꾸고자 할 때, 이러한 관계를 생각해서 step-size를 바꿀 수 있도록 영감을 제공해주게 된다. 만약 full-batch를 사용한다고 했을 때 $\gamma=0.1, N=100$ 으로 hyper parameter를 선택하면 좋을 것이다. 그러나 계산량을 개선하기 위해서 SGD를 사용할 때 mini-batch의 크기를 10으로 줄인다고 했을 때 약 10배가 줄었기 때문에 10배를 곱해서 $\gamma=1$ 로 업데이트 해야할 것이다. 즉, mini-batch의 크기를 어떻게 설정하느냐에 따라서 step-size를 자연스럽게 바꿀 수가 있다는 것이다.

Reason for Using SGD

이렇게 data의 양이 엄청 많을 때 계산량을 줄이기 위해서 SGD는 매우 유용한 방법이다. 또한 SGD는 full-batch보다 optimal point를 찾는데에도 도움이 될 것이다. 만약 local minimum이 하나 있고 global minimum이 하나 있을 때, randomness가 없는 GD를 사용하게 된다면 full-batch의 gradient를 사용해서 local minimum에 빠질 위험이 존재한다. 왜냐하면 randomness가 없고 때때로 잘못된 초기값을 설정하게 되면 이러한 상황이 가능해진다. 반대로 randomness를 가지게 된다면 SGD는 이러한 local minimum을 빠져나갈 기회를 제공받게 되고, global minimum을 찾을 수가 있게 된다. 이러한 이유 때문에 현실에서는 SGD를 굉장히 많이 사용하게 된다. Deep learning을 할 때에도 full-batch보다는 mini-batch를 주로 사용하는 이유기도 하다.