ML and Probability Theory
Machine Learning에서 확률 이론은 꽤 중요한 부분이다. 이전에 machine learning은 데이터로부터 볼 수 있는 특정한 pattern을 학습하는 것으로부터 일종의 function을 만드는 과정이라고 했다. 여기서 pattern을 데이터가 나타내는 정보라고 생각해도 좋다.
간단한 예시를 한 번 보자. 확률 이론에서 가장 많이 등장하는 예시가 보통 주사위와 동전이다. 여기서는 동전을 던지는 상황을 가정해볼 것이다. 동전을 던지는 상황에서 생길 수 있는 결과는 동전의 앞면(H)이 하늘을 바라보거나, 동전의 뒷면(T)이 하늘을 바라보는 경우이다. 10번의 동전 던지기를 한다고 생각했을 때, TTHHHTHTHT라는 결과가 나왔다고 하자. 우리가 여기서 해야할 일은 이 다음에 나올 동전이 H인지 T인지 예측해야하는 것이다. H와 T가 나올 확률은 정확이 반이다. 그렇기 때문에 확률적으로 다음에 H가 나올 확률도 0.5이고 T가 나올 확률도 0.5인 것이다.
확률과 통계라는 개념이 실제로는 데이터의 특정한 pattern을 표현하는데 실로 유용한 것이다. 사람들이 일상 생활 속에서 확률을 생각하는 경우가 빈번하다. 확률을 통해서 미래의 일을 어느정도는 그럴듯하게 예측이 가능하기 때문이다. 반면에, 통계적으로 생각하는 경우도 자주 볼 수 있다. 왜냐하면 과거의 일들을 통해서 상황을 분석할 수 있는 것이 통계이기 때문이다. 결국, 과거나 미래의 상황에 대한 이해를 하기에 가장 관련이 있는 수학적 개념이 확률과 통계이기 때문에 machine learning에서는 probability와 statistic을 중요하게 생각하는 것이다.
Probability
확률이란 어떤 사건이 실제로 일어날 것인지 혹은 일어났는지에 대한 것을 나타내는 일종의 방법인데, 확률이 왜 재미있냐하고 하면 우리가 살아가는 인생은 전부 불확실한 상황들로 둘러싸여 있기 때문이다. 우리는 이러한 uncertainty를 수학적으로 표현하고 싶은데, 이것을 표현하는 방법이 확률이 되는 것이다. 요즘 가장 대두가 되고 있는 집의 가격을 예측하는 상황이나 비가오는지 가늠이 안가는 날씨같은 것들도 전부 확률과 관련이 있다. 여기서 우리가 집의 가격을 예측하는 상황을 생각해보자. 보통 집의 가격은 평수에 비례하는 경우가 대부분이다. 그렇지만, 실제로 집의 가격을 나타내는 요인으로는 이외에도 여러가지가 있다. 우리는 이러한 요인, 혹은 특징을 feature라고 하는데 1개의 feature 보다는 더 많은 feature들을 통해서 더 나은 예측을 할 수 있다.
Probability Space
확률은 보통 1을 최대치로 하여 생각하는데, 이러한 확률의 공간을 우리는 probability space라고 하며, 이를 triple으로 (Ω, F, P)로 정의할 수 있다. 여기서 Ω는 sample space, F는 α-field, 그리고 P는 probability measure을 의미한다.
Sample Space(Ω)
표본 공간이라고 불리는 sample space는 실험의 모든 결과를 전부 모아놓은 집합을 말한다. 즉, 어떠한 상황에서의 결과가 존재할 때, 가능한 결과들을 모두 모아 하나의 집합으로 표현한 것을 말한다. 예를 들어, 연속적으로 두번의 동전을 던지는 상황을 생각해보면 Ω = {HH, TT, HT, TH}로 표기할 수 있다. 동전의 경우 앞면 혹은 뒷면이기 때문에 앞면이 2번, 뒷면이 2번, 앞면 1번 후 뒷면 1번, 혹은 뒷면 1번 후 앞면 1번이 가능하기 때문이다.
Event(E)
Sample space에서의 부분 집합을 사건, 즉 event라고 정의한다. 위의 예시에서 연속해서 동전을 2번을 던질 때, E = {HH}, {TT}, {HT, TH}, ... 등과 같이 일어날 수 있는 상황들 중 몇가지 상황을 나타낼 때를 말한다.
Field(F)
확률에서 field라는 개념은 확률 계산이 가능한 집합을 말하며 σ-field라고 주로 사용한다. σ-field는 만약에 어떠한 field가 합집합, 교집합, 그리고 여집합에 대해서 닫혀있으면(closed), 우리는 이를 σ-field라고 부른다. Event와 field를 생각해보면, event는 sample space의 부분 집합이고, field는 이러한 event를 원소로 갖는 집합이다. 즉, F의 원소 하나하나가 E에 해당하게 되는 것이다.
Probability Measure(P)
P는 Ω와 F가 주어졌을 때, 일종의 mappint function의 역할을 하게 된다. 그리고 다음의 조건을 만족해야 한다.
P는 양수이고, 공집합에 대한 P는 0, sample space 대한 P는 1이어야 한다. 0에서 1사이의 값을 mapping하게 되는 셈이다. 그리고 이 모든건 countable하고 pairwise disjoint set에 대한 것이어야 한다. 쉽게 생각해서 P가 하고 싶은 것은 사건 하나하나에 양의 실수값을 대응시키면서 특정한 조건을 만족하는 mapping function을 만드는 것이다.
Important Basic Property
지금부터 다루는 확률은 사실상 중, 고등학교 시절에 다루었던 개념들이 기반이기 때문에 용어만 새롭고 내용은 쉽게 이해할 수 있을 것이다. 그리고 모든 probability에 대해서 event A와 B가 있다고 가정하고 할 것이다.
Joint Probability
교집합으로 불리는 joint probability는 여러 사건이 동시에 일어날 때의 확률을 의미한다.
Marginal Probability
주변 확률인 marginal probability는 각 event가 가지는 확률을 의미한다.
Independence
A와 B가 independent(독립) 하다는 것은 두 사건이 서로 영향을 끼치지 않을 때를 말한다. 그래서 joint probability와 같이 어떠한 사건이 다른 사건에 영향을 끼치는 경우에 그냥 각 사건의 확률을 곱해주기만 하면 된다.
Conditional Probability
조건부 확률은 고등학교 시절에 많이 들었을 것이다. Conditional probability는 주어진 사건이 일어났다는 가정 하에 다른 한 사건이 일어날 확률이기에 서로 영향을 줄 수도 있고 아닐 수도 있다. 만약 서로 영향을 주게 된다면 우리는 다음과 같이 식을 전개할 수 있다.
하지만, 서로 영향을 주지 않는 사건들이라면, 즉 두 사건이 서로 independent하다면 conditional probability는 다음과 같다.
Marginalization
Marginal probability는 다른 사건이 일어나는 것과 상관 없이, 오로지 자신에 관심을 가지면 됐다. 만약 joint probability가 주어졌을 때, 즉 2개의 사건이 동시에 일어날 확률이 주어지게 되었을 때에 원하는 사건을 제외한 나머지는 관심이 없는 상태를 말한다.
지금까지 예로 들었던 동전을 던지는 상황을 생각해보면, 첫번째 동전이 어떻게 나오느냐에 따라서 두번째 동전이 영향을 받지 않게 된다. 즉, 두번째 동전의 입장에서는 첫번째 동전은 아무런 의미를 가지지 못하는 것이다. 우리는 두번째 동전이 H인 결과만을 중요하게 생각할 것이다. 그러면 첫번째 동전이 H일 수도 있지만 T일 수도 있다. 그래서 우리는 HH인 경우와 TH인 경우만 의미가 있는 것이다. 왜냐하면 두번째 동전이 H인 경우에만 관심이 있기 때문이다. 그래서 두번째 동전이 H인 경우에 대한 모든 case를 더할 것이고, 이것을 marginalization이라 하는 것이다.
위의 표에서 보다시피 A 동전이 H인 경우와 B 동전이 H인 경우만 궁금한 것이기 때문에, 이에 해당하는 확률을 전부 더해주면 되는 것이다. 그렇다면 이 상태에서 A와 B의 independence를 확인할 수 있다.
A가 H인 확률은 0.6이고, B가 H인 확률은 0.3이다. 만약 A와 B가 independent하다면 A의 H인 확률과 B의 H인 확률을 곱했을 때, A와 B가 모드 H인 확률인 0.1과 같으면 된다. 그러나 계산을 해보면 0.6과 0.3을 곱하면 0.18로 0.1과는 다른 값이 나오는 것을 알 수 있다. 이를 통해서 A와 B는 dependent함을 알 수 있는 것이고, 이를 해석하면 B에 대해서 자세히 관찰해보면 A에 대한 정보를 얻을 수 있게 되는 것이다.
Bayes' Theorem
Machine learning에서 자주 등장하는 개념으로 Bayes' theorem이 있다. 꽤 자주 등장하고 유용한 도구이기 때문에 알고 있으면 도움이 될 것이다. 먼저 식을 살펴보면 다음과 같다.
Machine learning에 대한 정리이기 때문에 자세한 풀이는 하지 않겠지만, 간단하게 이야기하면 A와 B의 translation 관계를 이용해서 문제에 접근하는 것이다. 우리가 알기를 원하는 것에 대한 해답을 얻기 위해서, 우리가 알고 있는 사실을 기반으로 문제를 해결하는 것이다.
가령 machine learning에서 x라는 관찰된 공간(observation)에 대해서 y라는 잠재적인, 즉 원하는 것들이 존재하는 공간(latent)에 대한 확률을 최대화 하는 y를 찾기를 원한다. 하지만 이는 계산적으로 어렵기 때문에 이를 순서를 변형하는 Bayes' theorem을 이용하면 유용하게 계산이 가능해진다.
Other Important Concept
확률에 대해서 추가로 중요한 개념들이 존재한다. Random variable, expectation 등 중요한 개념들을 간단하게 이야기해보고자 한다.
Random Variable
확률 변수라고 부르는 random variable은 일종의 mapping function이다. Sample space를 실수 값으로 mapping하여 확률적으로 계산이 용이하도록 만드는 것이 목표이다.
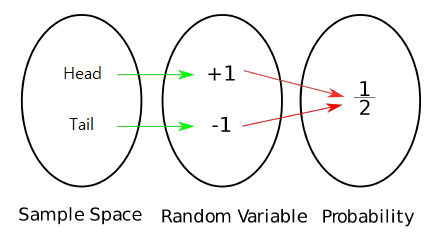동전을 예시로 H와 T라는 상황이 가능한데, H를 +1이라는 실수 값에 mapping하고, T를 -1이라는 실수 값에 mapping하는 변수를 random variable X로 생각할 것이다. 그러면 P(X = 1)은 0.5가 되고 P(X = -1)도 마찬가지로 0.5가 될 것이다. 실수 값을 이용해서 sample space의 특정한 상황을 mapping 한 것이다.
Probability Density Function(PDF)
나이, 주사위 등과 같이 어느정도 간격을 두고 마치 정수와 같이 떨어져 있는 변수를 discrete variable이라고 한다면, 키, 몸무게 등과 같이 연속적으로 마치 실수와 같은 변수를 continuous variable이라고 한다. 그리고 이러한 continuous variable의 확률을 모아놓은 분포를 확률 밀도 함수, 즉 probability density function(PDF)이라 한다. PDF는 모든 정의역에 대해서 항상 양수여야 하고, 전체 범위를 적분하게 되면 이는 확률의 최대치인 1이 된다. 그래서 우리는 PDF를 다음과 같이 적분 형태로 나타낼 수 있다.
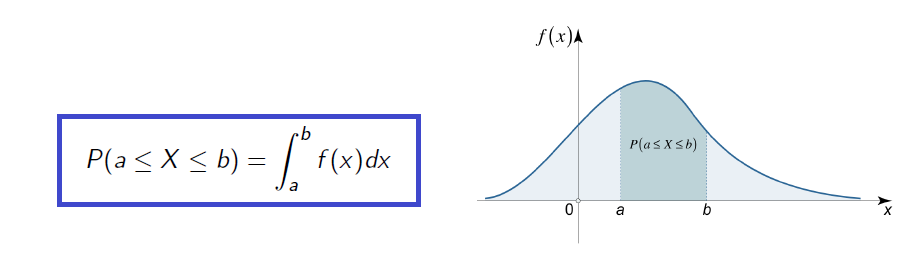위의 그림과 같이 적분한 값은 확률을 나타내는데, 이는 그래프의 아래 면적이 된다. 그래서 아래 면적의 총합은 1이 되는 것이다.
Cumulative Distribution Function(CDF)
누적 분포 함수라고 불리는 cumulative distribution function(CDF)은 어떤 확률 분포에 대해서 확률 변수가 특정 값보다 작거나 같은 확률을 나타낸다. Random variable X에 대해서 x라는 특정 상태들이 주어졌을 때, 우리는 다음과 같이 CDF를 나타낼 수 있다.
Discrete random variable에도 CDF가 있지만, continuous random variable에도 CDF가 있다.
그리고 이 CDF는 PDF를 적분하면 구할 수 있으며, PDF 또한 CDF를 미분하면 구할 수 있다.
