Expectations and Moments

이번에는 probability distribution을 나타내는 척도들에 대해서 알아보려고 한다.

Expectation

일상 생활 속에서 사람들은 어떤 확률적인 사건이 발생하려고 하면 자신에게 유리한 방향으로 생각하는 경향이 있다. 이러한 기대를 충족시키기 위해서 확률적으로 높은 경우를 택할 것이다. 수학적인 개념으로 기댓값이라고 하는 expectation은 간단하게 말해서 평균적인 기대치를 의미한다. 어떠한 확률을 가지는 사건을 무한히 반복했을 경우에 얻을 수 있는 값의 평균으로, 이를 기대할 수 있는 값을 우리는 expectation이라고 정의할 수 있다.

1부터 10까지의 평균은 1부터 10까지의 합계를 총 개수인 10으로 나눠주면 된다. 이를 확률에 적용하게 되었을 때에는 확률 변수에 해당하는 값과 이에 해당하는 확률을 전부곱해서 더해주면 평균이 되고 이 값이 바로 expectation이 되는 것이다.

이는 discrete variable에 해당하는 이야기이며, continuous variable에 대해서는 integral을 취해주면 된다.

The k-th Moment

Moment라는 것은 probability distribution을 나타내는 척도인 mean, variance 등을 계산할 때 활용이 가능하다. 가령 mean은 0에 대해서 1차 moment이고, variance는 mean에 대해서 2차 central moment이다. 이렇게 k차에 대한 moment를 k-th moment라 할 것이고 다음과 같이 정의할 수 있다.

Mean

Mean은 아마 대부분의 상황에서 사용이 될 것이다. Mean은 수학적으로 정의되는 평균값을 의미하며 first moment라고도 부를 수 있다. 그렇다면 이러한 mean과 expectation은 어떠한 차이가 있는 것일까? Mean은 sample data에서 주로 계산이 되는 반면에 expecation은 random variable의 weighted mean이 된다. 즉, random variable과 이에 해당하는 확률의 곱의 합으로 표현되는 것이다. Mean은 주어진 sample에 의존적이며, expecation은 random variable이 주어졌을 때 가장 높은 확률로 일어날 수 있는 기댓값이 되는 것이다.

예를 들어, 주사위를 3번 던졌을 때 {1, 2, 3}이 나왔다면 mean은 (1 + 2 + 3) / 3 = 2가 되는 것이고, expecation은 1 x 1/6 + 2 x 1/6 + 3 x 1/6 + 4 x 1/6 + 5 x 1/6 + 6 x 1/6 = 3.5이 되는 것이다. 물론 이러한 시행 횟수를 무한하게 늘린다면 뒤에서 보겠지만 mean은 expectation에 근사하게 될 것이다.

Variance and Covariance

Variance

Mean을 배우면 자연스럽게 variance도 배우게 된다. 분산이라고 하는 이 variance는 random variable이 expecated value로부터 얼마나 떠어진 곳에 분포하는지를 가늠하는 도구이다. 그리고 이를 second central moment라고도 칭한다. Expectation이 전체 data의 평균이라고 생각하게 되면, random variable에서 data의 위치를 어느정도 파악할 수 있다. 정의상으로 variance는 random variable X에서 평균을 뺀 값의 제곱의 합을 총 개수로 나눠준 값이 된다. 이를 정리하면 random variable X의 평균에 대하여 제곱의 expectation에서 X의 expecation의 제곱을 빼준 값이다.

Expecation이 같더라도 variance는 다를 수 있다. 만약 시험을 봤을 때, 평균이 50인 5명으로 구성된 2개의 집단이 있을 때 A 집단은 {40, 45, 50, 55, 60}이고 B 집단은 {10, 30, 50, 70, 90}이라고 했을 때 variance는 B 집단이 A 집단보다 크게 나타날 것이다.

Covariance

Covariance는 우리말로 공분산이다. 이는 2개의 random variable의 상관 정도를 나타내는 값으로, 다음과 같이 3가지 형태로 존재할 수 있다.
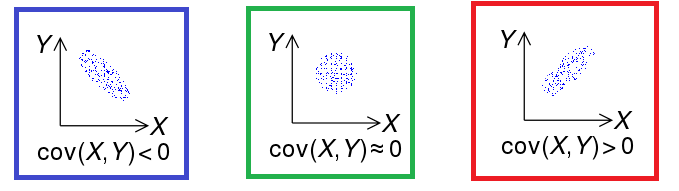만약 2개 중 하나의 값이 상승하는 경향을 보일 때, 나머지 하나의 값도 상승하는 경향을 보인다면 covariance의 값은 양수가 된다. 반대로 하나의 값이 상승하는 경향을 보일 때, 나머지 하나의 값이 하강하는 경향을 보인다면 covariance의 값은 음수가 된다. 그렇다면 covariance가 0이 되는 경우는 어떠한 경우일까? 바로 2개의 random variable이 independent하면 된다. 주의해야 할 부분은 꼭 independent하지 않더라도 covariance가 0이 될 수 있으니 알아두도록 한다. 이렇게 2개의 경향성을 파악하는 도구가 바로 covariance이다. 그리고 이는 수식적으로 다음과 같이 정의할 수 있다.

Expectation Property

2개의 random variable X와 Y, 그리고 constant c에 대해서 expectation의 성질을 알아보고자 한다. 생각보다 간단하지만 추후에 계산 등에 자주 이용되니 알아두면 좋을 것이다.

• $E(c)=c$
• $E(cX)=c\,E(X)$
• $E(E(X))=E(X)$
• $E(X+Y)=E(X)+E(Y)$
• $E(XY)=E(X)E(Y) \quad if\;X\;and\;Y\;are\;independent$

Variance Property

• $Var(c)=0$
• $Var(cX)=c^2\,Var(X)$
• $Var(X+c)=Var(X)$
• $Var(X+Y)=Var(X)+2\,Cov(X,Y)+Var(Y)=Var(X)+Var(Y)\quad if\;X\;and\;Y\;are\;independent$
• $Var(aX+bY)=Var(aX)+2\,Cov(aX,bY)+Var(bY)=a^2\,Var(X)+2ab\;Cov(X,Y)+b^2\,Var(bY)$

Covariance Property

• $Cov(X,X)=Var(X)$
• $Cov(X,Y)=Cov(Y,X)$
• $Cov(aX,bY)=ab\,Cov(X,Y)$
• $Cov(aX+b,Y)=a\,Cov(X,Y)$
• $Cov(X+a,Y+b)=Cov(X,Y)$
• $Cov(X+Y,Z)=Cov(X,Z)+Cov(Y,Z)$
• $Cov(X,aX+b)=a\,Var(X)$
• $Cov(aX+b,cX+d)=ac\,Var(X)$