[기계학습] Markov Decision Process(MDP) 2

JAEYOON SIM·2021년 12월 10일

Machine Learning

목록 보기

34/35

Value Function and Policy Evaluation(Prediction)

Value function이 주어졌을 때 non-trivial analysis를 이용해서 바로 expectation을 구할 수 있고, 이는 MDP의 종류와 주어지는 system에 의존하게 된다. 그러나 일발적으로는 미리 정의가 된 algorithm을 사용하게 되고, 이는 거의 모든 MDP에 사용이 가능하며 이러한 test를 policy evaluation이라고 한다. Policy evaluation은 prediction 문제를 푸는 것으로 현재 주어진 policy에 대한 true value function을 구하는 것이고 여기에는 Bellman equation을 사용하게 된다.

Recursion in Value Function

이를 위해서 기존의 value function을 recursive하게 다시 적을 필요가 있다. Recursive form이라는 것은 특정 state에서의 value function을 다른 state에서의 function으로 적을 수 있다는 의미이다.
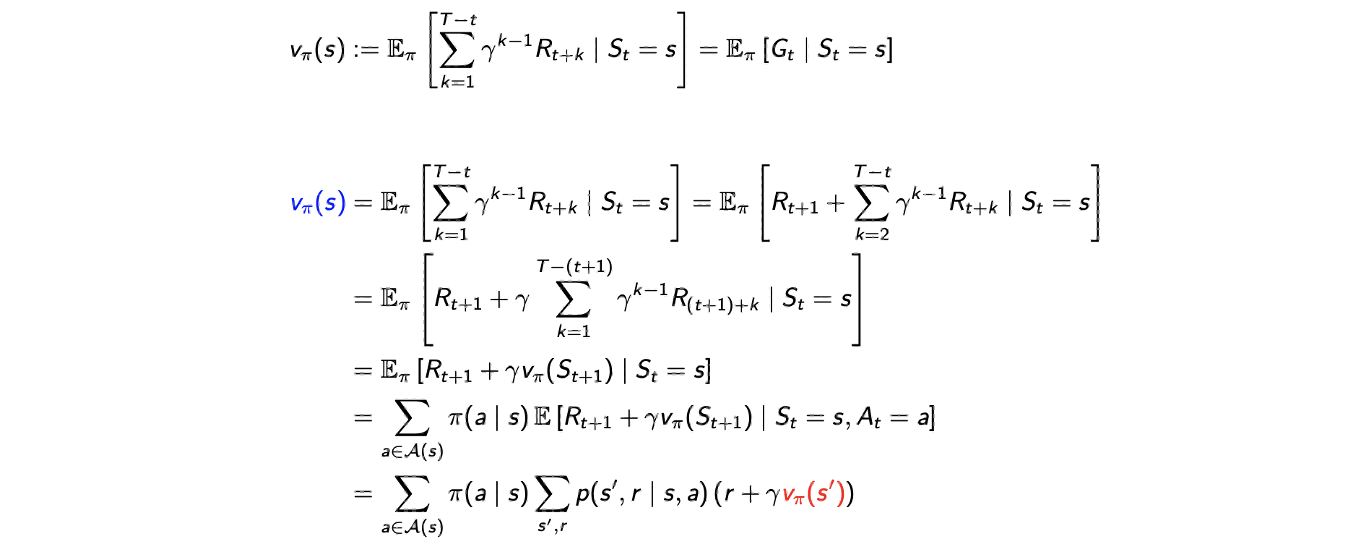이렇게 식을 적게 되면 $v_\pi(s)$ 식 안에 $v_\pi(s')$ 이라는 다른 state에서의 value function을 포함하게 된다. 이 식을 이해하기 위해서 value function의 기존의 정의로부터 시작할 것이다. 먼저 expectation 안에 있는 summation에서 $k=1$ 인 경우와 나머지를 분리시킬 것이다. 다시 $k=2$ 부터 시작하는 summation을 $k=1$ 부터인 식으로 reparameterization 할 것이다. $T$ 는 terminating time이고, reparameterization 된 summation의 경우 다시 $t+1$ 에서의 state value function으로 볼 수가 있다. 왜냐하면 이 식을 $t+1$ 에서의 state의 reward로 볼 수 있기 때문이다. 그러면 이제 policy와 transition probability를 알고 있다는 가정이 있으면, 즉 kernel을 알면 이 expecation을 간단하게 만들 수 있다. 그래서 최종적으로 마지막 등호를 성립하는 식으로 만들 수가 있다. Value function의 정의에 의해서 reculsive하게 정의를 하게 된 것이다.

Bellman Equation

이러한 reculsive relation은 Bellman equation으로도 알려져 있다. 왜냐하면 Bellman이라는 사람이 이러한 관계를 밝혀냈기 때문에 붙여진 이름이다.

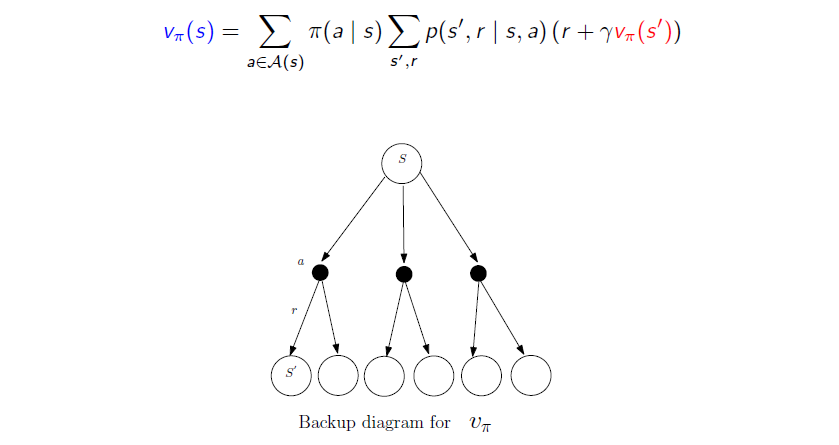
이 식은 위와 같은 graphical illustration으로 설명할 수 있다. 시작하는 state $s$ 로부터 value function $v_\pi(s)$ 를 구하고자 한다. $s$ 에서 policy $\pi$ 는 구체적인 action $a$ 를 probability $\pi(a|s)$ 로부터 선택하게 될 것이다. 어떠한 action을 고르느냐에 따라서 probability가 달라지게 된다. 하나의 구체적인 action을 고르게 되면 probability $p(r|s,a)$ 로부터 reward $r$ 을 얻게 될 것이다. 그러면 특정 action을 고르고 나면 $r$ 과 $a$ 에 의해서 summation으로 표현이 될 것이다.

Reward는 state $s'$ 이후의 과정에서도 계속해서 얻을 수가 있다. 그래서 $v_\pi(s')$ 으로부터 또 다른 reward를 얻으면서 결과적으로 이러한 과정이 reculsive하게 반복되게 된다. 그러나 이러한 과정은 다음 단계이기 때문에 식에서 다음 value function이 discounted factor $\gamma$ 와 함께 곱해져서 사용된다. $s'$ 이 random variable이므로 평균화해야 하며 이는 $s'$ 에서 동일한 summation 또는 action에 의해 수행된다. 이렇게 Bellman equation을 보았고, 이는 위의 식으로부터 도출할 수 있었다.

Value function을 찾는 것은 linear equation을 푸는 것과 같은 맥락이다. 왜냐하면 Bellman equation이 대안적으로 value function의 linear function으로 적을 수 있기 때문이다. 이를 이해하고자 $v_\pi$ 를 value vector로 적을 것이다. 이와 비슷하게 reward vector는 $R^\pi(s)$ 를 원소들로 나타낼 수 있으며, 각 원소는 특정 state $s$ 에서 policy $\pi$ 를 따르는 expected reward가 된다. 마지막으로 transition matrix는 $P^\pi(s,s')$ 를 원소로 나타낼 수 있으며, 각 원소는 policy $\pi$ 를 따르는 state $s$ 에서 $s'$ 으로의 transition probability가 된다. 시작 state $s$ 와 평균화한 action $a$ 로부터 action을 선택하는 probability와 이 특정 state에서의 $\pi(a|s)$ 로부터 우리가 얻고자 하는 것은 $s'$ 에 대한 transition probability이다.

v_\pi=\begin{bmatrix}v_\pi(s=1) \\ v_\pi(s=2) \\ \vdots \end{bmatrix}

Value vector, reward vector, transition matrix가 주어지게 되면 Bellman equation은 linear equation으로 대체하여 적을 수가 있다.

v_\pi=\underbrace{R^\pi+\gamma P^\pi v_pi}_{=\mathcal{B}^\pi (v_pi)}

그래서 value function을 찾는 것은 linear equation을 푸는 것과 같아지게 된다. 편의성을 위해서 이 linear equation을 Bellman operator $\mathcal{B}^\pi$ 로 나타낼 것이다. $\mathcal{B}$ 는 vector에서 vector로의 function이다.

Solving Linear Equation

Value function을 구하기 위해서 matrix inversion을 사용해서 바로 linear equation을 풀면 된다. 이를 위해서 다음과 같이 식을 좀 변형할 것이다.

v_\pi = R^\pi + \gamma P^\pi v_\pi

(I-\gamma P^\pi)v_\pi = R^\pi

v_\pi = (I-\gamma P^\pi)^{-1}R^\pi

이러한 과정을 거쳐서 transition matrix $P$ 와 reward vector $R$ 이 주어지면 value function을 완전히 구할 수가 있다. Marix inversion의 complexity가 $n$ 이 state의 개수라 할 때 $O(n^3)$ 으로 꽤 높기 때문에 computational intractable할 때도 존재한다. 그래서 다른 방법을 적용해야 할 수도 있으며, 이 방법으로는 iterative policy evalution algorithm 등을 사용하게 된다. $V_0$ 를 0 vector와 같이 임의로 $V$ 의 초기값으로부터 시작해서 계속해서 Bellam operation을 반복하게 된다.

V_{k+1}\leftarrow R^\pi+\gamma P^\pi V_k=\mathcal{B}^\pi V_k

그러다 보면 이 식은 true value function으로 수렴하게 된다.

V_1=R^\pi,\qquad V_2= R^\pi+\gamma P^\pi R^\pi, \qquad V_3= R^\pi+\gamma P^\pi R^\pi+(\gamma P^\pi)^2R^\pi, \qquad \dots

이렇게 계속 구할 수가 있으며, $V_1$ 은 time $T= 1$ 에서의 expected reward가 되고, $T$ 가 2가 되면 $V_2$ 를 얻게 된다. 이렇게 가다가 $k\geq T$ 가 되어 terminating time에 도달하게 되면 결국에는 true value function에 수렴하게 되어 원하는 결과를 구하게 되는 것이다. 결론적으로 일반적인 MDP의 전체 정보가 주어졌을 때 value function을 구하는 algorithm을 가지게 된 것이다.

Action-Value Function and Policy Iteration(Control)

이렇게 MDP가 주어졌을 때 우리는 더 나아가 optimal policy를 구하고 싶다. MDP에서 action이란 어떤 state에서 할 수 있는 행동들을 말하는데, 보통 모든 state에서 가능한 행동은 모두 같다. Value function에 대해서 생각을 해보면 state의 가치라는 것은 그 state에서 어떤 action을 했는지에 따라 달라지는 reward들에 대한 정보를 포함하고 있다. 또한 agent 입장에서 다음 action에 대해서 다음으로 가능한 state들의 value function으로 판단하는데, 이를 위해서 다음 state들의 대한 정보를 모두 다 알아야하고 그 state로 가려면 어떻게 해야하는 지도 알아야한다.

따라서 state에 대한 value function말고 action에 대한 value function도 구할 수 있으며, 이것이 바로 action value function이 된다. Action value function을 이용하면 기존의 state 관점에서 본 value function과는 달리 어떠한 action을 할지 action value function의 값을 보고 판단하면 되기 때문에 다음 state들의 value function을 알고 어떤 action을 했을 때 거기에 가게 될 확률을 알아야하는 일도 없어지게 된다.

Optimal Policy

우리가 원하는 optimal policy를 구하는 일은 non-trivial한 문제이다. 왜냐하면 optimal policy는 모든 가능한 policy에 대해서 value function들을 비교해야 하기 때문이다.

v_{\pi_\ast}(s) \geq v_\pi(s)

만약 단지 크기가 $O(|A|^{|S|})$ 인 deterministic policy의 왕에게만 집중하게 된다면, 각 state에서 우리는 최대한 $A$ 개의 옵션을 가지게 되므로 deterministic policy의 개수는 $|A|^{|S|}$ 가 된다. 이는 computational intractable한 문제가 있지만, Markov property 덕분에 optimal policy와 optimal value function을 구하는 방법을 찾을 수 있게 된다.

Action-Value Function a.k.a. Q-function

자세하기 이해하기 위해서 action-value function이라는 또 다른 value function을 정의해야 한다. 그리고 이는 또 다른 용어로 Q-function이라고 한다. Q-function은 policy $\pi$ 의 action-value function이고 이를 $q_\pi(s,a)$ 라고 정의할 것이다. 여기서 보면 input이 추가 된 것을 볼 수 있다. Value function $v_\pi$ 와는 다른 action $a$ 가 $s$ 외에 추가적인 input으로 사용되었다. 그래서 $q_\pi(s,a)$ 는 perturbation을 가지는 policy $\pi$ 의 value function이다. 여기서 perturbation은 오로지 처음 state $s$ 에서만 나타나고, state $s$ 에서 다음 policy 대신에 action $a$ 를 선택한다. 이렇게 처음에 action $a$ 를 선택한 이후에는 policy를 따르게 된다. 그러면 우리는 policy $\pi$ 를 기반으로 또 다른 policy를 생각할 수 있다. 그래서 $q_\pi(s,a)$ 는 perturbation으로 부터 누적된 expected reward가 될 것이다.

더 형식적으로 $q_\pi(s,a)$ 는 다른 condition이 주어졌을 때 동일한 누적된 reward의 conditional expecation으로 정의할 수 있다. 그리고 이 condition에는 action $A_t$ 가 추가된다. 그러면 이 식은 현재의 reward와 value function의 weighted summation으로 다시 나타낼 수 있다. 이것이 의미하는 바는 value function을 구하고 나면 몇번의 계산을 통해서 쉽게 Q-function을 구할 수가 있다는 것이다.

Q-function의 정의를 생각했을 때 주어진 policy $\pi$ 에 대해서 perturbation을 측정했을 때 $q_\pi(s,a)$ 가 $v_\pi(s)$ 보다 크다는 것은 특정 state $s$ 에서 policy $\pi$ 를 따르기 보다는 action $a$ 를 선택하는 것이 더 낫다는 것을 의미한다. 만약 $q_\pi$ 를 전체 $s,a$ 에 대해서 계산하게 되면, 모든 state에 대해서 $\operatorname*{arg\,max}_a q_\pi(s,a)$ 를 선택함으로써 현재의 policy $\pi$ 를 개선할 수 있을지도 모른다. 그리고 이렇게 선택된 새로운 policy를 $\pi'$ 라고 정하면 된다.

Policy Iteration

지금까지 현재 진행하는 policy에 따라 value function을 구하고(prediction) 이를 토대로 policy를 optimal하게 발전시키는(control) 흐름으로 진행이 된다. 이때 prediction의 과정이 policy evaluation이고, control의 과정이 policy improvement가 된다.

Policy improvement에서는 사용하는 Bellman equation에 따라 2가지 종류로 나뉘게 되는데 Bellman expectation equation을 사용하는 policy iteration과, Bellman optimality equation을 사용하는 value iteration으로 나뉘게 된다. 이러한 내용들을 기반으로 해서 먼저 policy iteration이라는 다음의 알고리즘을 보도록 하자.
먼저 value function의 initialization부터 시작한다. 모든 state에서 value function을 구하기 위한 policy evaluation이 진행된 이후에 우리는 Q-function을 찾게 될 것이고, 이는 계산된 $V$ 에 대응되는 $q(s,a)$ 가 될 것이다. 그리고 모든 state에서 이 $q(s,a)$ function에 argmax를 취하게 된다. 이로부터 우리는 이전에 정의 된 policy를 개선할 수 있고, 다시 policy evalutation으로 돌아가서 policy의 수렴성을 위해서 반복적으로 수행하게 된다.

Example of Policy Iteration

어떻게 policy iteration이 동작하는지 간단한 예시를 통해서 보도록 하자.

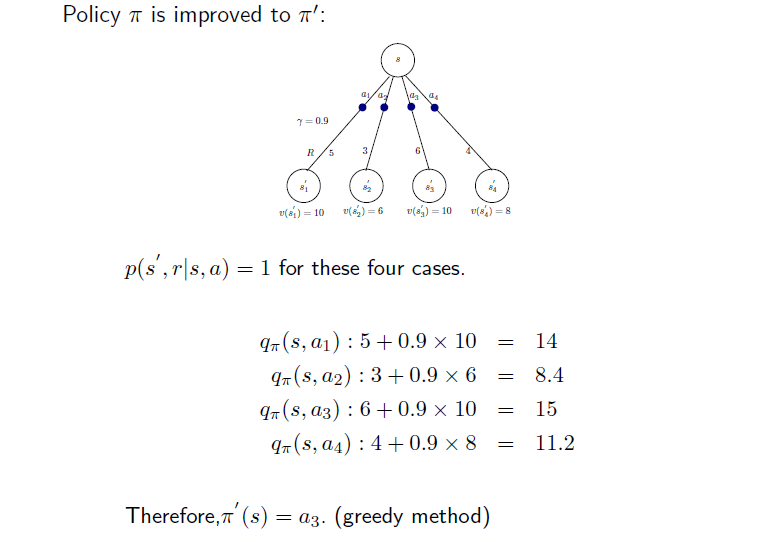
먼저 value function을 구하고 $q_\pi(s,a)$ 를 계산할 수가 있다. 처음 state $s$ 에 대해서 4개의 action $a$ 가 존재하고 각각에 대해서 reward $R$ 이 존재한다. 그리고 마지막에 value function $v$ 를 구하게 된다. 이 예시는 특정한 값으로 reward와 value를 예시로 든 것이다. 이로부터 $q$ function을 위와 같이 계산할 수 있다. $\pi$ 를 따르는 각 $a$ 에 대해서 reward와 value function에 discount factor를 곱해서 더하면 각각의 $q$ 값을 구하게 된다. Policy를 개선한다고 했을 때 다음 policy evaluation에서는 이전의 가장 높은 $q$ 값을 선택하게 된다.

Monotonic Improvement

Policy evaluation을 수행하고 policy improvement를 진행하는 policy iteration alogrithm에서 monotone improvement를 증명할 수 있다.

$\text{Lemma(Monotone)}$
$\text{For the successive value functions }V_k \text{ and } V_{k+1},$

V_{k+1} \geq V_k, \qquad \text{i.e., }V_{k+1}(s) \geq V_k(s) \quad \forall s \in S

Convergence of Policy Iteration

그리고 이는 policy iteration의 수렴성을 설명하고, 다음의 optimality를 결론지을 수 있다.

$\text{Theorem}$
$\text{Policy iteration eventually finds optimal policy }\pi_\ast \text{ s.t.}$

v_\ast(s):=v_{\pi_\ast}(s)=\operatorname*{max}_\pi v_\pi(s)\quad \forall s \in S

Policy iteration algorithm은 우리가 optimal policy에 도달할 때 수렴하게 된다.

Value Iteration

Policy iteration에 대한 한 가지 불만 사항으로 여러번의 policy evaluation이 필요하다는 것이다. 아마도 중간에 존재하는 모든 policy evaluation에서 많은 계산의 원인이 발생할지도 모른다. 그래서 optimal policy를 찾는 또 다른 방법으로 policy iteration과는 다른 value iteration을 제안할 수 있다.

이는 중간의 모든 policy를 평가하지 않고 한번에 진행하겠다는 것이며, 단지 value evaluation을 계산하려고 노력하는 동시에 improvement 하고자 하는 것이다. 자세한 내용을 이해하기 위해서 value iteration에서 사용 되는 또 다른 Bellman equation으로 optimal Bellman equation에 대해서 알아보려고 한다.

이미 optimal value function을 찾았다고 가정해보자. 그러면 이 optimal value function은 위의 optimal equation을 검증해야 한다. 현재의 optimal value를 $V(s)$ 라고 하면 Q-function의 최적의 값과 매칭되어야 하고 여기서 $a$ 의 최대를 취하게 된다. 그렇지 않으면 policy를 개선할 여지가 있으므로 value function의 optimality에 대한 우리의 가정을 위반하게 된다. 그래서 이 식은 max operation을 포함하고 있고, 이를 optimal Bellman equation이라 부르게 된다. 우리는 $\mathcal{B}^\ast$ 를 optimal Bellman operator라 부를 것이고 이제 이 식을 기반으로 다음의 value iteration algorithm을 생각해볼 수 있다.
먼저 value function을 임의로 초기화해서 시작하고 optimal Bellman eqaution을 기반으로 optimal value function을 반복적으로 계산을 하게 된다. 다음 단계에서 value function은 현재 예측된 값에 대응되는 Q-function의 action에 대한 max로 계산이 된다. 이는 policy evaluation과 동시에 policy improvement를 하는 것과 같은 셈이다. max operation을 취하는 것은 policy improvement이고 이전에 $q$ 를 계산하는 것이 policy evaluation과 같다.

Convergence of Value Iteration

이렇게 하고 나면 또 다시 optimal policy에 대한 value iteration도 수렴성을 증명할 수 있다.

Generalized Policy Iteration(GPI)

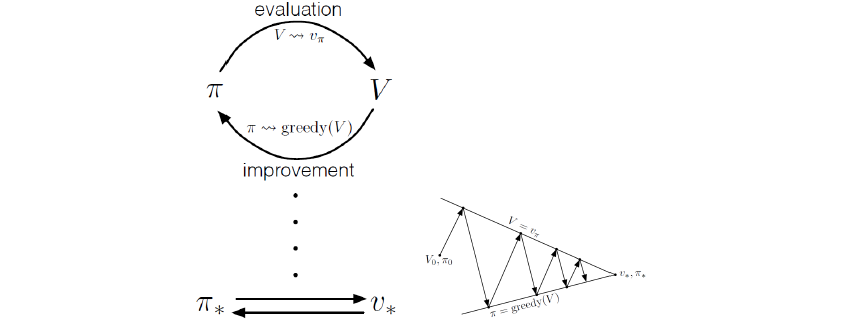대략적으로 이야기하면 먼저 특정 policy $\pi$ 에 대한 value function을 구하고 이를 $q$ function을 기반으로 greedy한 선택을 통해서 policy $\pi$ 를 개선시킨다. 그리고 개선시킨 후에 다시 policy를 업데이트 시킨며, 이를 기반으로 다시 개선을 시키게 된다. 이러한 과정을 수렴할 때까지 반복적으로 수행하게 되는데 전체적으로 이러한 과정은 꽤 자연스러워 보인다.

지금까지 policy iteration과 value iteration을 알아보았으며, 이는 optimal policy를 찾기 위한 기본적인 계산 algorithm들이었다. 이를 통해서 policy evaluation과 policy improvement를 반복적으로 수행하면 되고 각 algorithm은 optimal policy에 대한 수렴성을 보장하고 있다.