[기계학습] Markov Decision Process(MDP) 1

Markov Property and Definition of MDP

Markov decision process(MDP)는 reinforcement learning에서 가장 근본이 되고 기본적인 model이다.

Agent-Environment Interface

Decision process는 본질적으로 agent-environment interface에서 공식화될 수 있다. 여기에는 A.I.에 해당하는 agent와 system에 해당하는 environment가 있다.
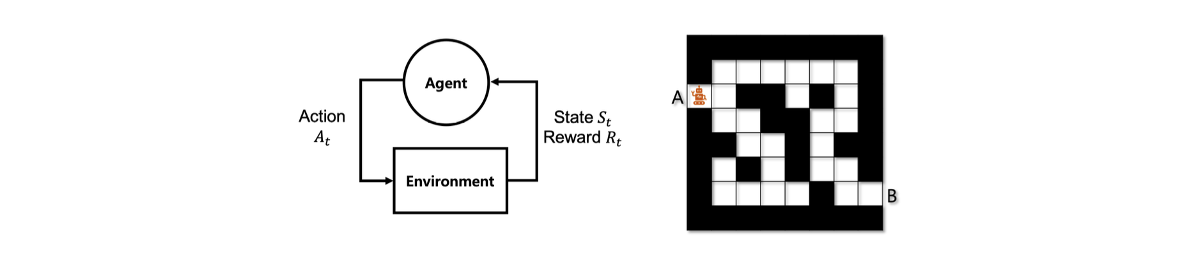Agent와 environment는 discrete time에 서로 상호작용하게 되는데, Discrete time이라는 것은 $t=0,1,2,\dots$와 같은 경우를 말한다. 각 step마다 environment는 state $S_t$와 reward $R_t$를 가지게 되며, state가 주어지면 agent는 system에 의해 주어진 reward를 최대로 만들 수 있는 행동을 결정하게 된다. 여기서 행동은 action $A_t$에 해당한다. 그래서 trajectory는 $(S_0, A_0, R_1, S_1, A_1, R_2, S_2, A_2)$와 같이 나타낼 수 있게되며, 이러한 것이 decision process이고 agent-envirionment interface가 되는 것이다.

Markov Decision Process(MDP)

MDP 또한 agent-environment interface에 해당하며 단지 decision process에 Markov property가 추가되었을 뿐이다. Markov property는 다음과 같이 하나의 간단한 식으로 나타낼 수 있다.

다음 state와 reward는 동일한 conditional distribution을 가지거나 서로 다른 condition을 가지게 된다. Condition 중 하나는 전체 history이고, 또 다른 condition은 현재의 state와 action이 주어지는 것이다. 현재의 state와 action이 다음 state와 reward의 distribution을 완전히 결정한다는 의미이다. 이러한 성질에 대해서 우리가 기대할 수 있는 바는 최적의 행동을 결정하고자 할 때 굳이 전체 history를 볼 필요가 없다는 것이다. 오로지 필요한 것은 현재의 state와 action의 요약된 정보이다. 이것이 Markov property가 보장하는 내용이다. 다음은 Markov property의 예시이다.
이 예시는 로봇이 입구 A로부터 출구 B를 찾아가야 하는 task를 보여주고 있다. 여기서 state는 미로인 map과 로봇의 현재 위치로 나타낼 수 있다. 로봇은 특정한 경로를 따라 이동했을 것이고 동일한 위치라도 다른 경로를 따라 이동했을 수도 있을 것이다. 현재 위와 같이 로봇이 멈춰 있을 때 다음은 어떠한 상황이 발생할까? 다음의 상황은 이전의 history와는 완전히 독립되어 있다. 즉, 로봇이 어디서 어떠한 경로로 도착했는지는 전혀 중요하지 않다. 현재의 구체적인 위치로부터 다음 단계의 distribution을 완전히 결정하게 된다. 위의 두 로봇이 같은 위치에 있을 때 이전의 경로와는 상관없이 위로도 갈 수 있고 옆으로도 갈 수가 있다. 이것이 Markov property의 예시가 된다. 만약 reinforcement learning을 적용하고자 한다면 가장 먼저 Markov property를 확인해야 한다.

Markov Decision Process: <S,A,R,p>

그렇다면 Markov property는 어떻게 확인할 수 있을까? 이는 조금 있다가 확인할 것이고 그 전에 Markov decision process의 notation에 대해서 알아보고자 한다. MDP는 총 4개의 요소를 이용해서 표현할 수 있으며, 앞의 3가지는 모든 가능한 state, action, reward의 space를 각각 나타낸 것이다. $\mathcal{S}$는 state space, $\mathcal{A}$는 action space, 그리고 $\mathcal{R}$은 reward space가 된다.

각각의 reward는 real number로 나타낸다. 여기서 reward를 어떠한 scalar로 나타낸다는 것은 정말 중요한 이야기다. 편의성을 위해서 대부분의 reinforcement learning framework는 reward를 vector보다는 real number로 나타내도록 가정한다. 이로부터 우리는 항상 어느 것이 더 나은지 결정할 수 있다.

마지막 4번째로 $p$는 정말 중요한 요소로 대부분의 reinforment learning이 이 $p$를 학습시키는데 초점을 맞추고 있다. $p$를 kernel이라고도 부르며 다음과 같이 conditional distribtuion으로 정의할 수 있다.

여기서 2개의 $\mathcal{S}$를 사용하는데 하나는 현재 state이고 다른 하나는 다음 state를 나타낸다. 현재 state로부터 action을 취하고 reward를 얻으며 다음 state로 이동하는 과정을 포함하고 있다. MDP는 Markov property를 가지고 있기에 이 kernel은 모든 가능한 dynamics를 MDP에 나타낸다. 왜냐하면 우리는 history에 신경 쓸 필요가 없고 현재의 state와 action이 더 중요하기 때문이다. 그리고 편의성을 위해서 다음과 같이 notation을 사용할 것이다.
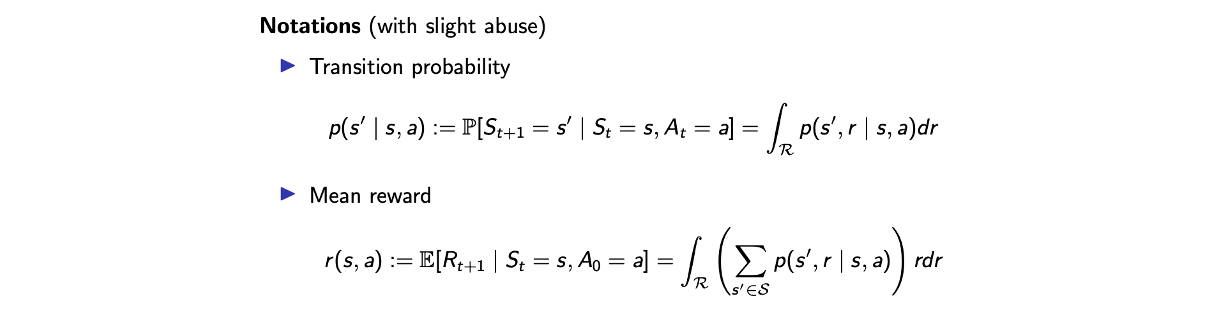먼저 transition probability는 input을 다르게하여 $p$를 재사용하고 있다. 현재 state $s$와 action $a$에 대해서 다음 state룰 $s'$이라고 했을 때 reward가 없다면 이는 state transition을 의미하게 된다. 그리고 state와 action을 input으로 $r$ function을 사용하게 된다면 mean reward를 나타낼 수 있다. Kernel $p$는 dynamics를 완전히 설명할 수 있어서, 일단 $p$를 알게 된다면 system의 완전한 emulation을 아는 것과 같아진다.

Example of Kernel

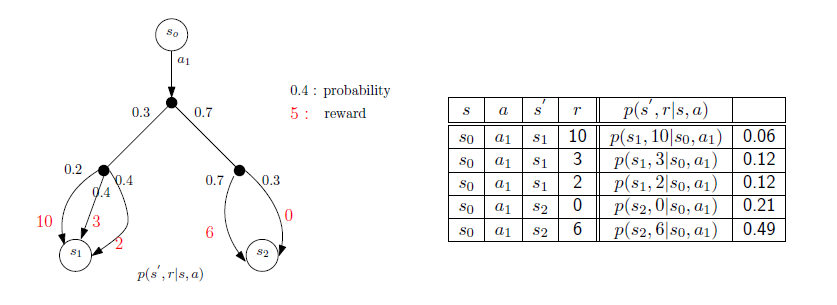위의 두 식은 kernel로부터 transition probability 혹은 mean reward로의 conversion을 보여주고, 바로 위의 diagram은 transition probability 혹은 mean reward에서 kernel로의 conversion을 보여주는 예시이다.

이 diagram을 이해하기 위해서 가장 먼저 $s_0, a_1$부터 시작하고자 한다. 이때 0.3의 확률로 $s_1$으로 가게되고 0.7의 확률로 $s_2$로 가게된다. 그리고 $s_1$로 간다고 했을 때 다시 0.2의 확률로 reward 10을 가지게 되고 0.4의 확률로 reward를 3, 2를 가지게 된다. State transition과 reward distribution에 따라 위의 diagram을 우측의 kernel로 바꿀 수가 있다. Kernel에서는 4개의 variable $s,a,s',r$이 input으로 사용되고 그 값은 transition 확률과 conditional reward distribution 확률을 곱해서 얻을 수 있다. $s'$과 $r$을 기반으로 확률을 곱해서 얻으면 된다.

Example of MDP

MDP는 표현하는 힘이 정말 강력해서 대부분의 reward를 가지는 상황에서 modeling에 사용되곤 한다. MDP에 의해서 modeling되는 상황들이 많지만 몇가지 예시를 보고자 한다.

Helicopter Control

첫번째로는 helicopter control이다. 먼저 장난감 비행기가 있다고 했을 떄 우리가 하고자 하는 것은 이 비행기가 원하는 궤적으로 날아가는 것이다.

비행기를 조종하기 위해서 system을 MDP에 맞추고자 한다. Agent는 controller, environment는 helicopter, state로는 위치, 방향, 속도 등이 있고, action은 helicopter의 controller에 의해서 정의하면 된다. 마지막으로 reward는 원하는 궤적에서의 편차의 음수와 같이 설정하면 된다. 만약 원하는 궤적과 실제 helicopter가 다르게 이동했다면 편차의 음수만큼 reward를 설정해야 한다. 이러한 reward에 대해서 optimal policy는 실제 궤적과 원하는 궤적을 일치하도록 만들기 위해서 helicopter를 완벽하게 통제할 수 있는 방안을 찾을 것이다.

Game Playing

또 다른 예시로는 알파고와 같은 game playing이 있다.
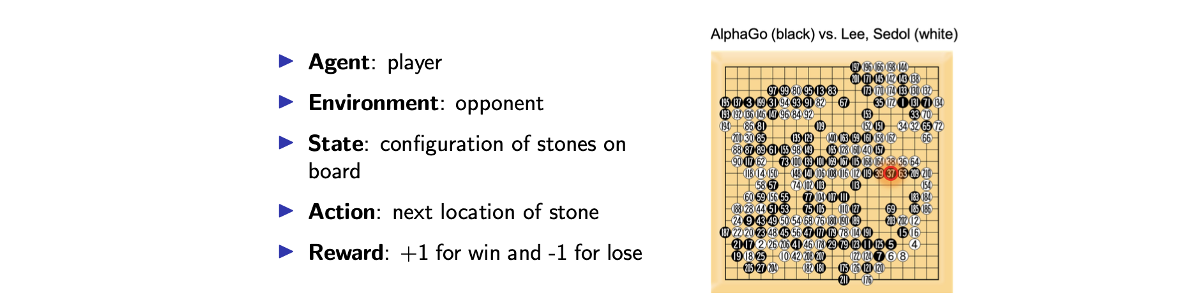여기서 agent는 1명의 player고, environment는 이 player의 opponent가 된다. 만약 agent가 알파고라면 environment를 이세돌 선수로 보면 된다. State는 바둑판의 알들이 어떻게 놓여있는지로 하면 되고, action은 agent 돌이 놓일 다음 위치로 정하면 된다. Reward는 게임이 끝날 때 승리했으면 +1, 패배했으면 -1로 주어질 것이다. 이 reward로 누가 승리했는지 알 수가 있다.

이러한 상황도 MDP에 해당한다. 왜냐하면 state와 action이 주어졌을 때 이는 확률적이지만 다음 미래는 현재의 state와 action에 의해서 완전히 설명될 수 있기 떄문이다. 이렇게 game playing을 modeling 했을 때 실제로 2016년도에 알파고가 이세돌 선수를 상대로 승리하는 모습을 보였다.

Inventory Management

이번에는 inventory management를 예시로 보았을 때 먼저 베이컨을 파는 가게가 있다고 가정할 것이다. 매주($t$)마다 가게는 지난 주 마지막에 남은 베이컨 상자 $S_t\in \{0,1,\dots,M\}$개를 가지고 있고, 이번주 시작에 $A_t$개의 상자가 주문되었다. 그리고 $D_t$는 $t$주에 요구되는 베이컨의 개수라고 할 것이다. 이를 기반으로 얼마나 많은 상자를 주문했고($C(t)$), 가게에 얼마나 많은 상자가 남아있고($h(t)$) 등을 고려해서 비용을 계산할 수 있다. $q$개의 제품을 팔았을 때의 수입을 $f(q)$라 하고 일주일에 한번 주문하면서 가게는 공간적인 제약 때문에 $M+1$개의 상자 이상을 가질 수 없다고 할 것이다. 이러한 여러 조건들을 가정하고 inventory management를 생각해보려고 한다. 이러한 내용들을 기반으로 먼저 다음과 같이 수식으로 정의하고자 한다.
Space 뿐만 아니라 transition function과 reward function도 정의할 수 있다. 우리의 inventory의 공간상의 제약 때문에 state space를 M까지만 정의한 것이다. Action space는 현재 state에 의존하기 때문에 위와 같이 설정한 것이다. 우리의 inventory에 이미 $s$개의 박스가 있다면 공간상의 제약 때문에 추가로 많은 양을 주문할 수 없다. 즉, 다음 state에서 M을 넘어가는 일은 발생해서는 안된다.

Transition probability는 우리가 $D$에 대해서 알게 되면 완전히 결정된다. 만약 현재 inventory가 충분하고 충분한 양의 박스를 주문한다면 결국 우리는 $S_t+A_t-D_t$개가 된다. 우리는 $S_t+A_t$개의 박스를 팔 수가 없다. 그래서 대괄호와 플러스 notation이 붙은 것이다. 이는 max operation으로 0과 괄호 안의 값을 비교하게 된다. 그래서 0개 아래로는 내려가지 못한다. Reward는 위에서 가정한 $h,C,f$에 의해서 직관적으로 나타낼 수 있다. $A_t$개의 상자를 주문하는데 드는 cost와 $S_t+A_t$개의 상자가 남아있는데 드는 cost와 해당하는 주의 시작과 끝의 박스의 개수의 차이에 따른 수입까지해서 reward를 나타낸 것이다.

이렇게 정의하고 나면 agent-environment interface를 나타낸 것이 된다. 이렇게까지 하지 않으면 MDP인지 알 수가 없다. 왜냐하면 Markov property를 확인해보지 않았기 때문이다. $D$는 주어진 상수로 여길 수 있지만, 아쉽게도 $D$는 이전의 history와 action에 의존하는 random variable이 될 수 있다. 그래서 Markov property를 보장하기 위해서는 time-indepent한 $D$를 가정할 필요가 있는 것이다. 만약 그렇지 않으면 이전의 history와 action에 의존해서 Markov에 해당하지 못하는 경우가 된다.

Policy

일단 MDP를 정의하고난 이후 우리가 원하는 것은 state가 주어졌을 때 action을 결정하는 최적의 function을 찾는 것이다. 이러한 과정을 policy라고 부른다. Policy는 state에서 action으로의 function이며, 다음과 같이 정의할 수 있다.

Policy는 state로부터 action의 distribution을 mapping하게 된다. 특히 policy가 각 state마다 오직 하나의 action을 선택한다면 deterministic하다고 이야기 할 수 있다. 이러한 경우에 notation의 편의성을 위해서 다음과 같이 mapping을 나타낼 수 있다.

그리고 policy가 모든 $t$에 대해서 constant이면 stationary하다고 이야기 할 수 있다. 만약 그렇지 못하다면 non-stationary policy가 된다. 다음의 예시가 non-stationay policy이다.

Stationay policy는 $\pi_0$는 $t_0$, $\pi_1$은 $t_1$과 같이 시간에 의존적이다. 위의 예시를 보면 $\pi_1$과 $\pi_2$가 다른 것을 볼 수 있다. Time 1에 $s_1$이 첫번째 action을 선택했는데 time 2에는 두번째 action을 선택하는 식으로 시간에 따라 달라지게 되는 것을 non-stationary policy라고 한다.

Goal in MDP

이러한 여러 정의들을 기반으로 이제부터 optimal policy에 대해서 정의할 수 있게 되었다. MDP의 목적은 optimal policy를 찾는 것이다. Optimal policy를 정의하는 방법은 여러가지가 존재하지만, 전형적인 방식은 discounted cumulated reward를 최대로 만드는 것이다. Optimal policy의 정의는 어떻게 우리가 long-term reward 혹은 cumulated reward를 정의했는지에 의존적이다. 그래서 여러 기준들과 방식이 있지만, discounted cumulated reward를 최대로 만드는 방식을 선택할 것이며, 우리가 흔히 아는 방식이 바로 이러한 것이다.

Value Function

이 방식은 다음과 같이 식으로 나타낼 수 있다. Agent가 state 1에 있다고 가정을 하자. 거기서부터 계속해서 action을 취해가면서 이동할 것이고, 그에 따라서 reward를 받는 것들을 기억할 것이다. 끝이 있는 episode라고 가정했을 때, episode가 끝났을 때 state 1에서부터 받았던 reward를 discounted factor를 적용해 다 더할 수 있다. Agent 가 다음으로 갈 수 있는 state들의 가치를 보고서 높은 가치의 state로 이동하게 되는데, 이는 policy에 따라 효율적이고 정확한 value function을 구하게 된다.

우리는 미래의 모든 reward의 weighted summation에 expectation을 취할 것이다. 만약 우리가 매우 좋지 못한 state를 초기값으로 설정한다면 좋은 결과와 reward를 기대하기는 어렵다. 그러나 때때로 좋은 상태의 state에서 시작한다면 더 좋은 결과와 reward를 기대할 수 있다. 이러한 식으로 policy는 초기 state에 대한 인식과 함께 평가되어야 한다. 이를 위해서 또 다른 notion을 policy를 평가하고자 정의하고자 한다. 이것이 바로 위에서 정의한 value function $v_\pi(s)$이다. 그리고 여기서의 value function은 state에 초점이 맞춰져 있는 state-value function이다.

$\pi$는 평가 될 policy에 해당하고 $s$는 초기의 state에 해당하게 된다. Value function은 discounted cumulated reward에 대응해서 위에서 expectation 안에 정의된다. 이 expectation은 현재의 state $s$가 주어졌을 때 time $t$부터 terminal time $T$까지 weighted reward의 summation에 대한 conditional distribution에 취해졌다. 여기서 $\gamma$는 discounted factor로, 만약 매우 먼 미래의 reward를 볼 수 있다면 불이익을 줄 것이고, 멀지 않은 미래에 동일한 reward를 보게 된다면 불이익을 많이 주지 않을 것이다. 이러한 내용을 $\gamma$에 의해서 정량화 할 수 있다. 그리고 위의 식을 보면 알겠지만 이러한 weighted summation을 $G_t$로 간단하게 나타냈으며, 이를 return이라고 부른다. 결국 return의 expection을 value function으로 정의하는 것이다.

그러면 이제 optimal policy를 정의할 준비를 마친 것이다. Value function을 모든 state마다 최대로 만드는 optimal policy는 다음과 같다.

여기서, maximization은 가능한 모든 policy에 대해 취해진다. 모든 policy라는 것은 일부 policy는 deterministic하지만 다른 일부 policy는 stochastic하다는 것이다. 심지어 non-stationay와 stationay한 경우도 모두 포함이 되는 것이다.

Example: Life MDP

Discounted cumulated value function을 이해하기 위해서 4개의 state를 가지는 life MDP라는 예시를 통해서 보도록 할 것이다.

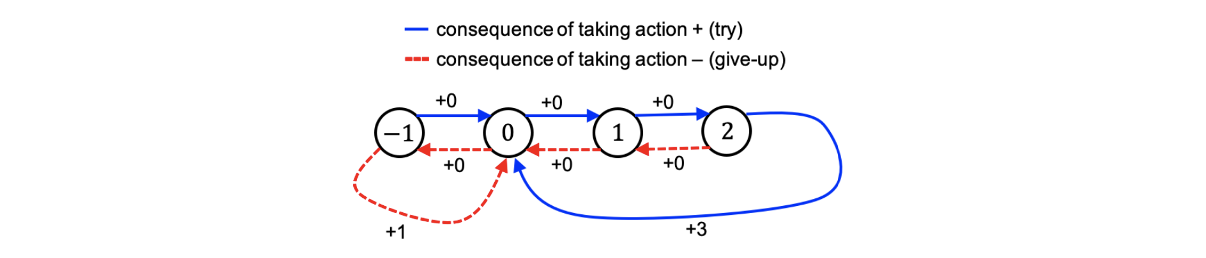4개의 state로 -1, 0, 1, 2가 있고 2개의 action으로 try와 give-up이 있다. 만약 계속 try한다면 state가 계속 올라갈 것이고 2에 도달해서도 try를 한다면 0으로 이동해서 reward로 +3을 얻게 된다. 반대로 give-up을 하는 경우에는 반대로 -1로 향할 것이고, -1에 도달해서 또 다시 give-up을 한다면 0으로 이동하면서 reward로 +1을 얻게 된다.

여기서 우리가 discounted factor를 크게 신경쓰지 않는다면 오직 average reward를 취하게 될 것이다. Optimal policy는 state -1인 경우를 제외하고는 계속해서 try를 선택해야 한다. 왜냐하면 평균적으로 위에서 length가 3인 파란 사이클은 사이클마다 +3의 reward를 얻어서 평균적으로 +1을 얻게 된다. 반면 매번 give-up을 선택한다면 사이클마다 +1의 reward를 얻어서 +1/2을 평균적으로 얻게 된다. 이렇게 어떻게 선택하느냐에 따라서 average reward가 달라지는 것을 볼 수 있다. 만약 시간이 충분하다면 계속 try할 것이지만, 때때로는 타협하기 위해서 give-up도 고를 것이다.

만약 discounted factor $\gamma$가 1에 매우 가까운 0.999일 때 optimal policy를 계산한다면, 이러한 경우에 optimal policy는 state가 0, 1, 2에서는 try를 선택하고 -1에서는 give-up을 선택할 것이다. 만약 현재 state가 -1이라면 try를 선택할 필요가 없다. Give-up을 1번해서 0으로 이동하는 것이 낫다. 이것이 discounted factor가 매우 큰 경우에 대한 optimal policy이다.

만약 discounted factor $\gamma$가 0에 매우 가까운 0.001일 때 optimal policy를 계산한다면, 이러한 경우에 optimal policy는 state가 -1, 0에서는 give-up을 선택하고 1, 2에서는 try를 선택할 것이다.

State가 0에서 optimal action은 discount factor에 의존하게 된다. $\gamma$에 따라서 때때로 try하지만 때로는 give-up을 선택할 수도 있다. 그러나 전형적으로 deep reinforcement learning에서는 1에 가까운 매우 큰 값을 선택하곤 한다.