.png)
확률 이론에 대해서 어느정도 알았다고 하더라도, 실제로 이러한 확률 이론이 어떻게 적용이 되고 사용이 되는지 의아할 수 있다. 그래서 이제 확률 이론이 실제로 machine learning이나 다른 분야에 어떻게 적용이 되는지 알아보려고 한다. 기본적이지만 확률 이론을 어떻게 사용할 수 있는지는 굉장히 중요한 내용이다. 그래서 쉬운 예시를 하나 들어보려고 한다. 먼저 앞면이 나올 확률이 인 동전을 가지고 있다고 해보자. 만약 10번의 동전을 던졌을 때, 7번의 앞면과 3번의 뒷면이 나올 확률을 묻는다면 어떻게 대답할 수 있을까?
가장 그럴듯한 대답은 일 것이다. 당연히 10번 중 7번에 해당하는 확률이라서 쉽게 답할 수 있을 것이다. 그렇다면, 이러한 사실이 정당화 될 수가 있을까? 이러한 결과는 어디서 얻게 된 것일까? 혹시 모를 다른 답이 존재할 수도 있다. 확률의 관점에서 우리는 observation을 하고 parameter를 추정한 것인데, 이는 사실 우리의 경험을 토대로 머리에서 나온 답이다. 이것도 하나의 확률을 추정하는 방법인 것이고, 지금부터는 여러가지 추정 방법에 대해서 알아보고자 한다. Machine learning 분야에서는 이 질문에 대해서 3가지 방식으로 답을 도출할 수 있다. 경험적으로 우리는 0.7이라고 답을 내리게 되지만, machine learning의 관점에서는 이와 비슷한 논리를 가지고 답을 말할 것이다. 사실 0.7이라는 답도 어떻게 보면 머릿 속에 어떠한 확률 모델이 존재하기 때문에 비롯된 결과이다.
Statistical Model: a Set of Probabilistic Models
Machine learning은 확률 모델을 만드는 방법을 제안하고 이로부터 특정 확률을 답으로 도출하게 된다. Machine learning이 말하고자 하는 바를 이해하기 위해서는 statistical model을 먼저 이해해야 한다. Machine learning은 주어진 목적을 달성하기 위해서 data로부터 특정 패턴 등을 찾아내는 방법론을 말하는데, 여기서 이러한 패턴을 찾기 위해서는 statistical model이라고 불리는 확률 모델들 중에서 관측이 된 data를 가장 그럴듯 하게 만들어낼 수 있는 확률 모델을 찾아야 한다. Machine learning에서는 필수적으로 먼저 확률 모델 하나를 가정하고 가장 가능성이 높고 그럴듯한 확률 모델을 찾는 것을 목표로 한다.
이러한 접근은 supervised learning과 unsupervised learning 모두에 사용이 되며, statistical model은 machine learning의 어느 분야에서든지 찾아볼 수 있다. Supervised learning에서는 라는 모델을 기반으로 input과 output을 mapping하는 방법을 학습하고자 하며, unsupervised learning에서는 input의 확률 모델인 를 설명하고자 하는 방법을 학습하고자 한다. Deep learning과 같이 parameter를 기반으로 추정을 해야하는 parameterized model이라면 supervised learning에서는 를, unsupervised learning에서는 를 학습해야 하는 것이다. 결국 우리는 statistical model로부터 가장 확률적이고 가능성이 높은 확률 모델을 찾는 것이 목표가 된다.
이번 parametric density estimation 방법들을 알아보기 위해서는 unsupervised learning에 초점을 맞춰서 model paratemter 로부터 data 를 나타내는 확률인 를 추정하고자 한다.
Typical Setupt for Statistical Model
Statistical model에서는 기본적으로 가정이 필요하다. 먼저, 개의 data 을 independent and identically distributed(i.i.d.)로 가정하고자 한다. 즉, 각 data 는 하나의 독립적인 분포로부터 나타나게 된다. 이렇게 보통 가정을 하게 되고, statistical model의 목표는 이러한 의 분포를 추정하고자 하는 것이다. 이는 를 찾는 것과 같은 이야기이다.
예를 들어서 여러 사람으로부터 각각의 형제, 자매 수에 대한 조사가 이뤄졌다고 해보자. 여기서 형제와 자매의 숫자는 random variable로 볼 수 있다. 물론 어떠한 상관관계가 존재할 수는 있으나, 가정에 따라서 서로 독립적이라고 할 것이다. 우리가 알고자하는 것은 이러한 조사를 기반으로 만들어지는 확률 분포이다. 형제와 자매의 숫자를 1부터 6까지 하고 7이상을 묶는다고 했을 때, 우리는 총 6개의 parameter가 필요하게 된다.
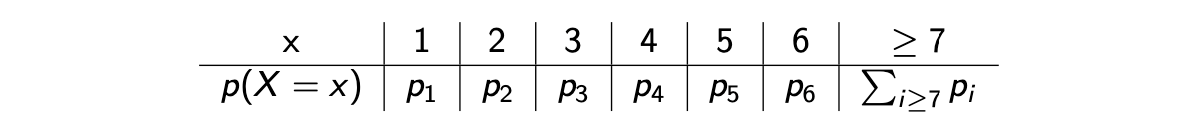 우리는 여기서 이렇게 parameter를 여러개 사용하기 보다 가 Poisson distribution을 따른다고 가정해서 하나의 parameter 만을 사용하고자 한다. 물론 어떠한 분포를 설정하는지에 따라 parameter의 수는 달라지게 된다. 이렇게 statistical distribtuion의 선택에 따라서 parameter 수를 조절할 수 있게 된다. 보통은 empirical distribtuion의 모양에 따라 사용하는 확률 분포를 선택하게 되고, 이에 따라 parameter 수는 결정되게 된다. Statistical model을 설정하는 것도 조금 있다가 알아보도록 할 것이다. 우리가 우선 초점을 맞추고자 하는 것은 statistical model이 주어졌을 때 가장 확률적으로 그럴듯한 확률 모델을 찾는 방법에 대한 것이고, 이를 위해서 확률 모델을 결정지을 수 있는 model parameter를 추정하고자 한다.
우리는 여기서 이렇게 parameter를 여러개 사용하기 보다 가 Poisson distribution을 따른다고 가정해서 하나의 parameter 만을 사용하고자 한다. 물론 어떠한 분포를 설정하는지에 따라 parameter의 수는 달라지게 된다. 이렇게 statistical distribtuion의 선택에 따라서 parameter 수를 조절할 수 있게 된다. 보통은 empirical distribtuion의 모양에 따라 사용하는 확률 분포를 선택하게 되고, 이에 따라 parameter 수는 결정되게 된다. Statistical model을 설정하는 것도 조금 있다가 알아보도록 할 것이다. 우리가 우선 초점을 맞추고자 하는 것은 statistical model이 주어졌을 때 가장 확률적으로 그럴듯한 확률 모델을 찾는 방법에 대한 것이고, 이를 위해서 확률 모델을 결정지을 수 있는 model parameter를 추정하고자 한다.
Density Estimation
이렇게 density estimation의 방법으로 parametric estimation이 존재하고, 이를 중점적으로 알아볼 것이다. Parametric estimation은 parameter들에 의해서 정해지는 density model에 대해서 특정 식을 가정하여 data를 가장 잘 설명할 수 있는 parameter를 찾고자 하는 것이다. 이외에도 density estimation으로 nonparametric estimation이 있고, 이는 다른 말로 kernel method라고도 한다.
Parametric estimation에서 하고자 하는 것은 Poisson distribution이라고 하면 전체적으로 empirical distribtuion과의 차이를 가장 줄일 수 있는 최적의 parameter 를 찾는 것이다. 우리는 특정 구역에서 empirical distribution과 우리의 estimation이 같기를 원한다. 하지만 현실에서 이는 거의 불가능 하며, Poisson distribtuion의 경우 오직 하나의 parameter로 결정이 되기 때문에 대표적인 구간에서조차 일치시키는 것이 거의 불가능하다. 이러한 경우에 nonparametric estimation을 사용하게 되면, kernel을 사용하여 명시적으로 parameter와 관찰한 data 사이의 상관관계를 만들어서 parametric estimation에서 존재하던 제약을 어느정도 해결할 수 있다는 장점이 존재한다. Kernel method는 continuous random variable에 대해서 유용하게 사용이 된다. 왜냐하면 empirical distribtuion은 보통 discrete distribtuion인데 우리가 추정하고자 하는 것은 보통 continuous distribtuion인 경우가 많다. 극단적으로 discrete distribtuion과 continuous distribtuion을 비교하고자 할 때, 일반적으로는 비교가 불가능하지만 kernel method를 사용하게 되면 이러한 문제를 해결할 수 있으며 유용하게 사용이 가능하다.
더 나아가 이러한 2가지 방식을 적절히 섞어서 사용하는 것을 semi-parametric estimation이라고 하며, 이는 흔히 최근에 많이 사용하는 neural network나 mixture model에 해당하게 된다. 더 심화된 machine learning 기법들에서는 이러한 semi-parametric estimation의 중요도가 더 올라가게 된다.
Parameter Estimation
Parameter estimation 혹은 density estimation에 대해서 조금 더 알아보자면, 우리는 먼저 에 의해 parameterize 된 distribtuion의 class, family 에 대해서 가정할 것이다. 여기서 는 parameter의 집합이고, 는 Bernoulli distribution이라면 일 것이고 normal distribution 이라면 와 같은 확률 분포일 것이다. 이렇게 parameter estimation은 Bernoulli, Gaussian 등과 같은 probability measure의 family로부터 시작하게 될 것이다. Family라고 하지만 간단하게 생각해서 우리가 아는 흔히 널리 사용되는 확률 분포들을 의미하게 된다. Family라는 이름은 그저 parameter의 변화에 따라 모양이 바뀌기 때문에 붙여진 이름이다.
이렇게 sample space와 probability measure의 family로부터 statistical model을 나타낼 것이고, 우리는 이러한 statistical model이 잘 명시되었다고 가정할 것이다. 즉, 가 우리가 고려하는 parameter 집합에 존재한다는 것이고, 이는 true distribution 가 로 설명이 된다는 것을 의미한다. Family distribution이 주어졌을 때 true distribution이 존재하게 된다. 이러한 것이 전형적인 가정이고, 만약 이러한 가정이 없다면 많이 어려워질 것이다. 여기서 를 true parameter라고 하며, 이는 미지수로 우리가 찾고자 하는 latent parameter를 의미한다. 그래서 i.i.d.를 만족하는 어떠한 연속적인 data의 관찰이 있을 때 우리는 true parameter 를 찾고자 한다.
물론 바로 에 대해서 추정해서 찾을 수 있지만, 가 가지는 특별한 의미와 성질들도 확인하고 싶을 것이다. 그러나 일반적으로 statistical problem에서 근본적인 issue는 true parameter 를 찾는 것이다. 우리가 흔히 수학적인 표기로 어떠한 parameter 등에 hat을 씌우는 것은 estimated value를 의미하게 된다. 그래서 우리의 목표는 true parameter와 가장 유사한 parameter를 추정하는 것이고(), 이렇게 찾은 estimator 는 bias와 variance 등에 의해서 얼마나 잘 찾았는지 확인해볼 수 있다. 당연히 는 data를 기반으로 한 esitmator이다.
Bias는 우리의 estimated value의 expecation과 true parameter 차이를 측정하도록 한다. 즉, 실제와 우리의 예측이 얼마나 편향되어 있는지를 판단하는 척도이다. Variance는 우리의 estimation의 randomness 혹은 uncertainty를 나타내게 된다. 이 2가지는 만족스러운 estimator를 찾기 위한 기본적인 척도가 되며, bias와 variance를 최소로 만들려고 해야한다. Machine learning에서는 다음과 같이 정의되는 risk를 최소로 하기를 원한다.
이는 가장 유명한 estimator measure이며 이는 mean squared error로부터 등장하게 되었다.
이렇게 mean squared error로부터 bias와 variance로 이뤄진 식을 만들 수 있으며, 매우 자연스럽게 계산이 가능하다. 그리고 굳이 mean squared error가 아니어도 estimator의 퀄리티를 측정할 수가 있다. 다만 MSE는 널리 사용되는 기본적인 measure이다.
Maximum Likelihood Estimation(MLE)
이제부터 MLE라고 불리는 maximum likelihood estimation에 대해서 알아볼 것이다. 계속해서 data, parameter에 대해서 likelihood에 대한 이야기를 했었고, 형식적인 정의는 다음과 같다.
Likelihood는 parameter 와 data 에 대한 함수이며, 이는 로부터 data point의 probability이기도 하다. Likelihood는 parameter 의 여러 값에 대한 관측치가 어떻게 있는지를 나타낸다. 그러면 MLE는 likelihood를 최대로 만들고자 하는 것이고, 이는 likelihood를 최대로 하는 parameter 를 찾는 과정이다.
여기서 likelihood function은 true parameter 에 대한 어떠한 정보를 필요로하지 않는다. MLE에서 likelihood function은 단지 dataset에 대한 함수일 뿐이다.
Maximum log-Likelihood Estimation
계속해서 i.i.d.를 가정해왔기 때문에 log function을 사용해도 괜찮다. 그래서 우리 log-likelihood를 사용해서 MLE를 하고자 한다.
log의 성질은 monotonically increasing하기 때문에 다음과 같이 적어도 괜찮다.
MLE에서 기존의 likelihood를 최대로하고자 했다면, 이제는 log-likelihood를 최대로하고자 하며 이는 동일한 맥락으로 해석이 가능하다. 우리가 각 data point들이 계속해서 i.i.d.를 만족하기 때문에 로 나타낼 수 있고, 이는 다음과 같이 likelihood function으로 정리할 수 있다.
i.i.d.를 만족해서 probability distribtuion의 곱으로 나타낼 수 있는 것이고, 이는 log의 성질을 더하면 summation으로 정의가 되는 것이다. log를 사용하지 않으면 곱셈의 성질 때문에 다루기 굉장히 어려운 형태가 되는데, log를 사용해서 likelihood를 정의하게 되면 최적화같은 것에서 수학적으로 다루기 쉬워지게 된다.
Interpretation of MLE
MLE를 좀 더 직관적으로 해석해보려고 한다. Dataset 의 각 sample이 라는 분포로부터 i.i.d.를 만족하면서 나타난다고 가정해볼 것이다. 그러면 dataset으로부터 empirical distribution이 다음과 같이 존재하게 된다.
여기서 는 Dirac-delta function으로 보통 좌표계 상에서 point를 정의하고자 사용한다. Model fitting 혹은 parametric density estimation은 dataset으로부터 만들어진 empirical distribtuion과 parameter 에 의해 만들어진 model 사이의 거리를 최소화 함으로써 진행이 된다.
KL Divergence
2개의 distribution의 거리를 최소화 한다는 것은 어떠한 의미를 가질까? 어떻게하면 2개의 distribution 사이의 거리를 줄일 수 있다는 것일까? 수학적으로 유명한 Kullback-Leibler(KL) divergence를 이용해서 그 의미를 판단해보고자 한다. KL divergence는 2개의 distribtuion을 비교하는데 있어 매우 유명한 distance measure 중 하나이다. 실제로 물리적인 차이를 나타낸다기 보다는 의미적으로 차이를 비교하고 정량화하는데 사용이 된다. 보통은 관찰한 결과를 앞에 쓰고 추정하고자 하는 것을 뒤에 쓰게 된다. 정의상 log의 weighted summation으로 weight로는 첫번째 distribtuion을 사용하기 때문이다.
2개의 distribtuion을 비교하기 위한 척도로 KL divergence를 선택했을 때, MLE와 KL matching 사이의 다음과 같은 correspondence를 가지게 된다.
는 empirical distribtuion이고 는 model 를 나타낸다. MLE는 실제로 에 의해 설명되는 퀄리티를 최대로 높이고자 하는 것이다. KL divergence를 보면 우리가 관찰했던 것과 추정한 것의 차이를 줄이려고 한다.
MLE = KL Matching
그리고 MLE가 KL Matching과 같다는 것은 다음과 같이 증명이 가능한 부분이다.
 첫번째 등호는 KL matching의 정의로 설명이 가능하다. 두번째 등호는 log에 의해서 parameter 에 독립되는 부분과 의존하는 부분으로 나눈 것이다. 특히 독립된 부분은 entropy 로 대체할 수 있다. 그리고 이 부분은 와 무관하기 때문에 constant 취급을 할 것이다. 세번째 등호는 남은 부분의 부호를 반대로 해서 minimization에서 maximization으로 바꾸고 empirical distribtuion을 적은 것이다. 네번째 등호는 integral과 summation을 바꾸면 Dirac-delta function의 정의에 의해서 와 같이 바꿀 수가 있다. 따라서 그 결과는 log-liklihood를 maximization하는 것과 같으므로 independent observation이라는 가정에 따라서 MLE와 같아지게 된다. 이렇게 MLE와 KL matching이 동일하다는 증명을 마칠 수가 있다.
첫번째 등호는 KL matching의 정의로 설명이 가능하다. 두번째 등호는 log에 의해서 parameter 에 독립되는 부분과 의존하는 부분으로 나눈 것이다. 특히 독립된 부분은 entropy 로 대체할 수 있다. 그리고 이 부분은 와 무관하기 때문에 constant 취급을 할 것이다. 세번째 등호는 남은 부분의 부호를 반대로 해서 minimization에서 maximization으로 바꾸고 empirical distribtuion을 적은 것이다. 네번째 등호는 integral과 summation을 바꾸면 Dirac-delta function의 정의에 의해서 와 같이 바꿀 수가 있다. 따라서 그 결과는 log-liklihood를 maximization하는 것과 같으므로 independent observation이라는 가정에 따라서 MLE와 같아지게 된다. 이렇게 MLE와 KL matching이 동일하다는 증명을 마칠 수가 있다.
Example of MLE
Example 1: Binomial Distribution
MLE의 예시로 먼저 binomial distribtuion에 대해 살펴보려고 한다. 대표적으로 번의 동전던지기를 생각할 수 있다. 번 던져서 앞면이 번 나왔다는 것을 이라는 미지수 가 있는 binomial distribtuion으로부터 관찰할 수 있다. 각 동전 던지기는 독립적이고 우리는 여기서 앞면이 나올 확률 를 최대한 가능성이 높도록 찾고자 한다. 는 binomial random variable이고 은 이미 알고 있는 값이다. 그래서 우리의 관찰한 결과를 가장 적절하게 설명할 수 있는 를 찾을 것이다. MLE의 해는 다음과 같이 log-likelihood function을 최대로 해야 한다.
이 식을 최대로 한다는 것은 결국 위의 식이 concave function이기 때문에 stationary point를 찾아서 해당 지점의 를 찾아야한다. 그래서 에 관한 derivative를 구해서 0으로 두어 구하면 된다.
Example 2: Gaussian Distribution
다음으로는 널리 쓰이는 normal distribtuion에 대해서 살펴볼 것이다. 가 i.i.d.를 만족하면서 normal distribtuion 를 따른다고 해보자. 이번에는 미지수가 2개로 와 를 추정해야 한다. 이번에는 2가지 상황을 생각해보려고 한다.
첫번째 estimator는 첫번째 sample만을 통해서 이라고 할 것이다. 직관적으로 알겠지만, 이는 매우 부적절한 추정일 것이다. 이렇게 되면 다음과 같은 결과를 얻을 것이다.
두번째 estimator는 모든 sample들의 평균을 취하는 empirical mean을 통해서 라고 할 것이다. 이렇게 되면 에 대해서는 다음과 같을 것이다.
이렇게 2개의 estimator가 있으면 2번째 estimator가 더 뛰어나다는 것을 알 수 있다. 왜냐하면 2개의 estimator 모두 unbiased라서 각 expectation이 true mean 와 같게 되지만, 첫번째 variance가 훨씬 큰 값을 가지게 된다.
Variance가 크다는 것은 더 많은 불확실성을 가지게 되어 더 risk를 안게 된다. 이러한 이유 때문에 2번째 estimator가 1번째 estimator보다 더 낫다고 이야기 할 수 있다. 우리가 결국 필요한 것은 risk가 작은 estimator이다. 직관적으로 empirical mean이 MLE의 첫번째 해라는 것을 알 수 있지만, 똑같이 log-likelihood로부터 미분해서 stationay point를 구하게 되면 최적의 와 를 구할 수 있다.

