[기계학습] ML and Probability Theory 3

JAEYOON SIM·2021년 9월 23일

Machine Learning

목록 보기

5/35

Sample Mean

Random variable의 합은 machine learning에서 흥미로운 내용이다. 흔히 어떤 집단의 평균을 추정하기 위해서 우리는 다음의 sample mean을 사용할 수 있다.

E(X) \approx \frac{1}{n}\sum_{i=1}^{n}x_i

Sample mean(표본 평균) 은 모집단의 평균과는 대비되는 개념이다. Random variable에 대해서 표본들을 추출하고 이 추출된 표본들의 평균을 구하게 되는데, 이 값이 평균의 집단을 대표하는 값이 된다.

우리는 전체 모집단으로부터 표본들을 무작위로 뽑았을 때, 이들의 평균이 어떻게 될 지가 궁금하다. Law of large number(큰 수의 법칙) 에 따르면 동일한 조사를 몇번이고 시행할 때, 표본들의 평균의 분포가 추출하는 표본들의 개수에 의존하는 것을 보여주었다. 그러나 실제로는 표본들의 평균이 어떠한 분포를 나타내는지는 정확히 모른다. 단지 표본의 수가 많아질수록 표본들의 분산이 줄어든다는 정보만 알 수가 있다.

큰수의 법칙이 말하고 싶은 것은 모든 표본들이 서로 독립적이고 그 분산이 bound가 되어 있다면, 표본들의 숫자가 증가함에 따라서 다음과 같이 sample mean이 실제 기대값에 수렴하게 된다는 내용이다.

\frac{1}{n}\sum_{i=1}^{n}x_i \rightarrow_p E(X) \quad as \; n\rightarrow\infty

Bernoulli Distribution

Bernoulli distribution(베르누이 분포) 은 반복되는 시행마다 결과가 오로지 2가지만 일어나게 되고 1번 시행하게 되었을 때의 분포를 이야기 한다. 이러한 상황은 그 결과에 따라 random variable X에 대해서 0과 1로 결정이 된다. 오로지 매개 변수 p만이 분포의 모양을 결정하게 되고, 만약 1로 결정이 된 x에 대해서 그 확률은 p가 되고, 나머지 0인 x에 대해서는 확률이 1에서 p를 뺀 값이 되게 된다. 흔히 1은 성공적인 상황에 대해서 부여되고, 0은 실패적인 상황에 부여되게 된다. 이는 조금 있다가 살펴볼 binomial distribution의 특수한 상황이다.

Bernoulli distribution $Ber(p)$ with parameter $p\in[0,1]$

P(X=x)=p^x(1-p)^{1-x}=p\quad if\;x=1

P(X=x)=p^x(1-p)^{1-x}=1-p\quad if\;x=0

그리고, 이 분포상에서 평균과 분산은 다음과 같이 구할 수 있다. 계산 과정이 어렵지 않기 때문에, 계산해보면 된다.

E(X)=p

Var(X)=p(1-p)

Binomial Distribution

Binomial distribution(이항 분포) 은 이 또한 매 시행마다 결과가 2가지만 일어나게 되고 매개 변수로는 확률값 p와 시행 횟수 n을 사용할 것이다. 어떠한 실험에 대해서 n번 반복한다고 생각했을 때, 각 실험은 성공과 실패에 따라서 성공하면 1, 실패하면 0을 부여받게 될 것이고, random variabel X에 대해서 n번 동안 실험을 해서 1과 0에 대한 확률을 알아보려고 한다.

간단하게 예시를 들어보자. 먼저 4번의 실험을 할 것이고, 성공 확률이 p인 실험이 3번 성공하고 1번 실패했다고 가정해보자. 이러한 경우 확률은 1000, 0100, 0010, 0001의 4가지 경우에 대해서 생각할 수 있다. $p$ 가 3번에, $1-p$ 가 1번이기 때문에 각 상황이 발생할 확률은 모두 $p^3(1-p)^1$ 일 것이다. 따라서, 4번의 반복 실험에서 3번이 성공할 확률은 $4\times p^3(1-p)^1$ 이 되고, 여기서 4는 4번의 시행 중 3번의 성공이 순서가 없기 때문에 조합( $_4C_3$ )으로 생각할 수 있다.

Binomial distribution $Bin(p,n)$ with parameters $p\in[0,1]$ and $n\in N$

P(X=x)=\binom{n}{x}p^x(1-p)^{n-x}\quad where\;\binom{n}{x}=\frac{n!}{x!(n-x)!}

주목할만한 사실로 binomial distribution에서의 random variable은 n개의 independent한 bernoulli distribution의 random variable의 합으로 해석이 가능하다.

이 분포상에서 평균과 분산은 다음과 같이 구할 수 있다.

E(X)=np

Var(X)=np(1-p)

Law of large number의 예시로 다음과 같이 계산이 가능하다.

E\left(\frac{X}{n}\right)=p

Var\left(\frac{X}{n}\right)=\frac{p(1-p)}{n}\rightarrow_{n\rightarrow\infty}0

Beta Distribution

Beta distribution(베타 분포) 은 굉장히 중요한 분포 중 하나로 이 분포에 대해서 이해하는 것이 굉장히 중요하다. Beta distribution에는 양수인 2개의 매개변수 α, β가 있고, 이에 따라서 [0,1] 구간을 정의할 수 있다. 2개의 매개변수는 분포의 형태를 결정지을 수 있고, 0과 1사이에서 정의가 되는 부분은 연속적인 값을 가지게 된다. Bernoulli나 binomial distribution과 같이 성공과 실패에 대한 2가지 선택을 다룬 분포이지만, 다른점은 이전 분포들은 성공과 실패의 횟수가 random variable이 되지만, beta distribution은 성공과 실패의 비율이 random variable이 된다. 그렇기 때문에 이 분포는 비율이나 백분율로 된 random variable를 예측하는데 유용하다.

Beta distribution $Beta(\alpha,\beta)$ with parameters $\alpha,\beta>0$

P(X=x)\propto x^{\alpha-1}(1-x)^{\beta-1}

주목할만한 사실은 beta distribution은 종종 bernoulli distribution의 모델 변수 p로 사용이 된다. 0부터 1까지의 값을 가질 수 있는 bernoulli distributino의 $p$ 의 값을 베이지안 추정한 결과를 표현한 것이다. 여기서 베이지안 추정은 $p$ 가 가질 수 있는 모든 값에 대한 가능성을 확률 분포로 나타낸 것을 말한다.

이 분포상에서 평균과 분산은 다음과 같이 구할 수 있다.

E(X)=\frac{\alpha}{\alpha+\beta}

Var(X)=\frac{\alpha\beta}{(\alpha+\beta)^2(\alpha+\beta+1)}

다음은 베타 분포의 α, β 값에 따라서 probability density function이 어떻게 그려지는지에 대한 그래프이다.
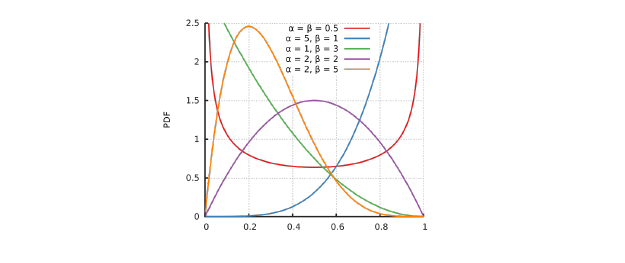α와 β가 모두 0.5인 경우나 2인 경우를 보면 random variable의 값이 0.5를 기준으로 대칭인 것을 알 수가 있다. 즉, α와 β가 같은 값을 가지면 좌우 대칭의 모양을 가져 균일해지며, α가 더 크게되면 1에 비대칭도를 가지게 되어 데이터의 평균이 분포보다 오른쪽으로, α가 더 작게되면 0에 비대칭도를 가지게 되어 데이터의 평균이 분포보다 왼쪽으로 치우치게 된다.

그렇기 때문에 beta distribution은 α와 β의 값을 바꿔주기만 하면 다양하게 확률 모형을 나타낼 수 있어 적용성이 높아진다. 여기서 α와 β는 각각 성공과 실패의 횟수라고 생각하면 되고, α=1, β=1인 경우는 성공과 실패의 확률이 0.5가 될 것이다. 이는 성공과 실패라는 2가지의 경우만 존재하고 어떠한 정보도 모른다면 예측하기 어렵다는 이야기가 된다. α=2, β=1인 경우는 성공의 확률이 0.66..이고 실패의 확률이 0.33..이 되어 기대값이 올라가게 된다. α=3, β=1으로 값을 수정하면 성공의 확률이 0.75가 되어 기대값이 더 올라가게 될 것이다. 만약, 여기서 실험이 실패해서 α=3, β=2가 되면 성공의 확률은 0.6으로 기대값이 조금 떨어지게 될 것이다.

Gaussian Distribution

Gaussian distribution은 normal distribution이라고도 불리며, 연속 확률 분포 중 하나로 평균과 표준 편차라는 2가지의 매개 변수를 통해서 분포 모양을 결정하게 된다. 이 분포는 평균을 기준으로 좌우 대칭의 종 모양을 나타낸다.

Gaussian distribution $N(\mu,\sigma^2)$ with parameters $\mu\in R$ and $\sigma^2>0$

P(X)=\frac{1}{\sqrt{2\pi\sigma^2}}exp\left(-\frac{1}{2\sigma^2}(X-\mu)^2\right)

Gaussian distribution은 기대값과 중앙값이 같다는 성질이 있다. 그리고 이 분포는 평균과 표준 편차가 주어져 있을 때 엔트로피를 최대화 하는 분포이다.

이 분포상에서 평균과 분산은 매개 변수 그 자체이기 때문에 따로 계산이 필요하지는 않는다.

E(X)=\mu

Var(X)=\sigma^2

그리고 Gaussian distribution에서 normalize를 하게 되면 평균은 0으로, 표준 편차는 1로 만들 수가 있다.

Z=\frac{X-\mu}{\sigma}

이를 Z-distribution이라고 부르기도 하는데, 이는 기준이 다양하게 만들어진 gaussian distribution을 하나의 기준으로 바꿔줌으로써 비교를 수월하게 만들 수 있다는 장점이 있는 것이다.

Lindeberg-Levy Central Limit Theorem(CLT)

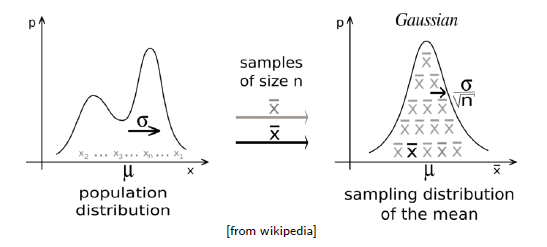
Lindeberg-Levy Central Limit theorem(중심 극한 정리) 은 모집단에서 표본을 뽑을 때, 표본의 크기 n이 커질수록 sample mean의 분포가 Gaussian distribution에 가까워지는 이론이다. 이때, 모집단의 분포와는 상관이 없다. 모집단이 한쪽으로 쏠려 있거나 알 수 없어도, 표본의 크기만 크면 sample mean의 분포는 Gaussian distribution에 가까워지게 된다. 이때, 이 정리가 성립하기 위해서는 최소한 표본을 30개 이상을 뽑아야만 한다.

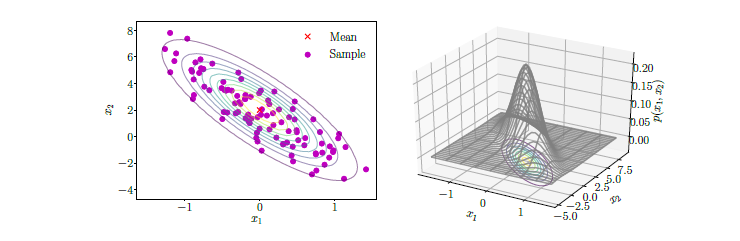
Multivariate Gaussian PDF

Gaussian distribution이 하나의 random variable에 대한 분포라면, Multivariate Gaussian dsitribution은 여러개의 random variable에 대한 분포이다. 차원을 1차원에서 다차원으로 확장했다고 생각하면 된다. 다음은 $x_1$ 과 $x_2$ 라는 random variable이 2개인 상황에 대한 예시이다. 좌측은 2차원 평면위에 점들과 등고선을 표현한 것이고, 우측은 등고선을 3차원으로 높이까지 표현한 것이다.

P(X|\mu,Σ)=(2\pi)^{-D/2}|Σ|^{-1/2}exp\left(-\frac{1}{2}(X-\mu)^TΣ^{-1}(X-\mu)\right)

차원이 늘어났기 때문에 모든 변수가 값에서 벡터 혹은 행렬로 표현이 될 것이다. X는 random variable들을 모아 놓은 벡터, $\mu$ 는 mean을 모아 놓은 벡터, Σ는 covariance을 모아놓은 행렬이 된다.

X=\begin{bmatrix}x_1\\x_2\\x_3\end{bmatrix}, \mu=\begin{bmatrix}\mu_1\\\mu_2\\\mu_3\end{bmatrix}, Σ=\begin{bmatrix}Σ_{1,1}&Σ_{1,2}& Σ_{1,3}\\Σ_{2,1}&Σ_{2,2}& Σ_{2,3}\\Σ_{3,1}&Σ_{3,2}& Σ_{3,3}\end{bmatrix}

Random variable의 개수가 늘어나면 그만큼 차원도 늘어나게 되어 계산은 복잡해질 수 있다. 그리고 mean과 covariance의 계산은 다음과 같다.

\mu :=E(X)

\sum :=E\big((X-\mu)(X-\mu)^T\big)=\sum_x(x-\mu)(x-\mu)^TP(X=x)

i.e.\quad\sum_{i,j}=Cov(X_i,X_j) := E\Big(\big(X_i-E(X_i)(X_j-E(X_j)\big)\Big)

만약 multivariate Guassian distribution이 n차원이라면 다음과 같을 것이다.

P(X)=\frac{1}{\sqrt{(2\pi)^{n}|Σ|}}exp\left(-\frac{1}{2}(X-\mu)^TΣ^{-1}(X-\mu)\right)

Illustraion of Covariance

Correlation은 2개의 random variable간에 어떠한 선형적 또는 비선형적인 관계를 가지고 있는지에 대한 정보이다. 두 변수가 서로 독립적일 수도 있고, 상관된 관계일 수도 있다.
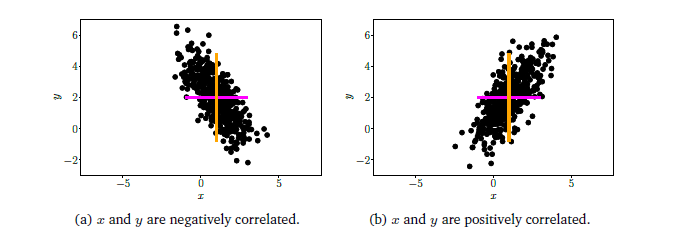Covariance 값은 X와 Y의 영향을 받기 때문에 이 값을 각각의 표준 편차로 나누어 주면 correlation을 구할 수가 있다.