[기계학습] Support Vector Machine 1

JAEYOON SIM·2021년 10월 7일

machine learning

Machine Learning

목록 보기

15/35

Maximum Margin Classifier

Support vector machine(SVM)은 classification의 유명한 방법 중 하나이다. Classification을 위해서 classifier를 어떻게 만들지에 대해서 알아볼 것이다.

Recap) Regression for Classification

Linear regression은 다음의 probability를 linear model에 근사시키고자 했다.

p(y=1|x) \approx w^T\phi(x)

그리고 logistic regression은 동일한 probability를 logistic model에 근사시키고자 했다.

p(y=1|x) \approx \frac{1}{1+\text{exp}(-w^T\phi(x))}

Classification은 어떠한 방식의 classifier를 사용하든지간에 classifier가 결론적으로 하고자 하는 것은 hyperplane을 그려서 decision boundary를 통해 data를 나누고자 하는 것이다.

Good Separating Hyperplane

아무래도 만족스러운 classifier를 만들기 위해서 수식적으로 확률로 접근하여 classification을 이해하는 것 보다 그래프 등의 graphical illustration을 통해서 이해하는 것이 더 쉽게 다가올 것이다. 그래서 예를 들어 2차원의 input과 2개의 class가 존재한다고 가정해볼 것이고, 다음과 같이 hyperplane이 2개의 class를 가지는 data point들을 분류하도록 할 것이다.

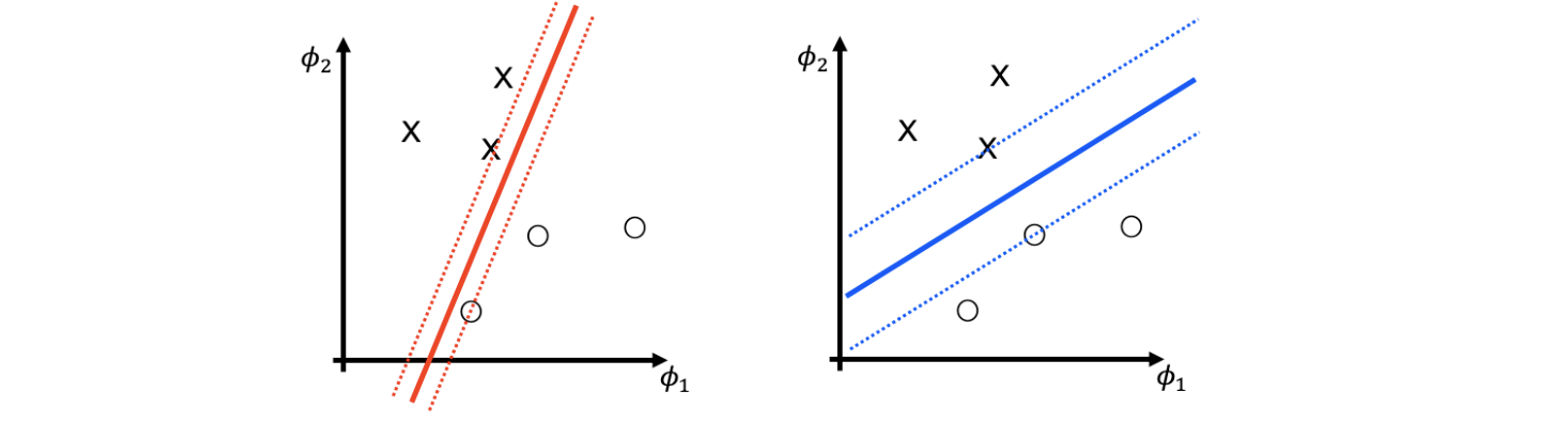빨간선과 파란선 모두 classification error는 0이라는 동일한 결과를 가진다. 그러나 사람이라면 2개의 결과를 놓고 어느것을 더 선호한다고 물어봤을 때 대부분이 우측의 파란선을 선택할 것이다. 이러한 이유는 파란선의 hyperplane으로부터 data들과의 거리가 더 멀기 때문이다. 즉, 더 큰 margin을 선호한다는 이야기이며 여기서 margin은 classifier와 data point들 사이의 최소한의 거리를 이야기한다. 결국 margin이 더 큰 쪽의 classifier를 사람들은 더 선호하게 되는 것이다.

그렇다면 logistric regression은 가장 큰 margin을 보장할 수 있을까? 만약 우리가 정말로 이러한 margin이 최대가 되기를 원한다면 이러한 hyperplane을 만들 수 있는 직접적인 방법이 존재할까? 이러한 궁금증을 해결하는 것이 이번에 살펴 볼 내용의 핵심이다.

Margin

우리가 원하는 margin을 최대로 만들기 위해서 margin을 형식적으로 정의할 필요가 있다. 그리하여 먼저 decision boundary를 다음과 같은 linear function으로 가정하고자 한다.

f(x) := w^Tx+b = 0 \text{ (for given }b > 0 \text{)}

$w$ 는 hyperplane에 대해서 orthogonal vector이고 $b$ 는 일종의 bias이다. 그러면 data point $x$ 와 decision boundary 사이의 거리를 수학적으로 정의하면 다음과 같을 것이다.

\text{distance: }\frac{|f(x)|}{||w||}

그리고 margin은 이러한 거리 중에서 가장 작은 거리를 나타낸 것이다.

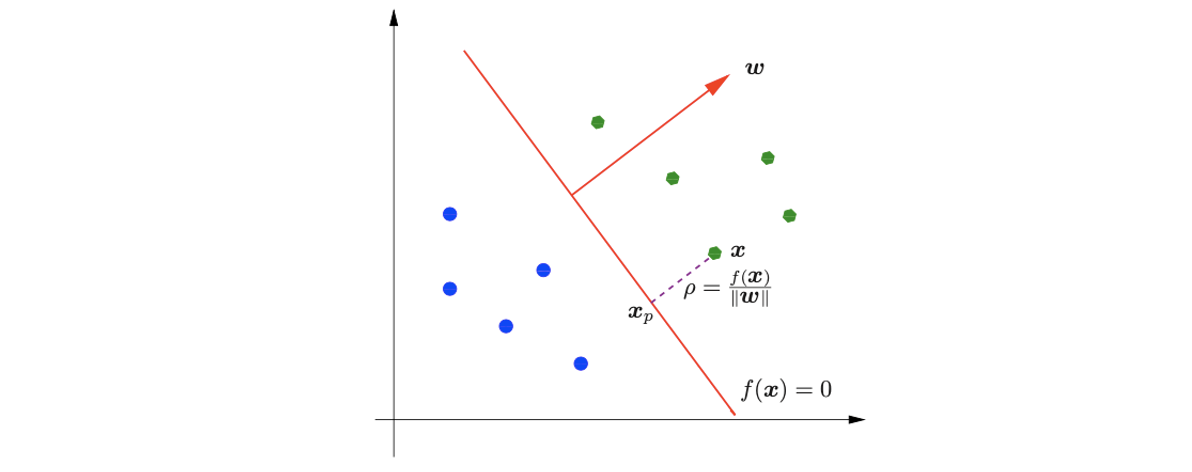\text{margin: } \operatorname*{min}_i \frac{|f(x_i)|}{||w||}

사실 distance가 왜 이렇게 정의되는지 굳이 이해할 필요는 없다. 이는 linear algebra에 의해서 당연하게 정의가 되는 내용으로 핵심은 우리가 여기서 하고자 하는 것이 error는 최소한으로 줄이면서 이러한 margin을 최대한으로 만들고자 하는 것이다. 그래서 problem을 다음과 같이 정의하고 싶다고 생각할 수도 있다.

\operatorname*{max}_w \operatorname*{min}_i \frac{f(x_i)}{||w||}

하지만 이렇게 정의하게되면 이러한 problem을 해결해주는 최적의 $w$ 가 무한히 존재할 수 있다는 것이다. 왜냐하면 hyperplane $w^Tx+b=0$ 은 non-zero constant $\lambda$ 에 의해 여러개로 나타낼 수 있기 때문이다.

\{x|w^Tx+b=0\}=\{x|\lambda(w^Tx+b)=0\}

이렇게 2개의 hyperplane이 동일해지고, 결국 이것이 의미하는 것은 우리가 원하는 하나의 solution이 아닌 무한히 많은 solution이 가능해진다는 것이다. $(\lambda w,\lambda b)$ 가 $(w,b)$ 와 동일한 hyperplane을 설명하고 이때 $\lambda$ 의 값은 non-zero이면서 $w$ 가 최대가 될 때 $\lambda w$ 도 최대가 되기 때문에 결국 solution이 무한해지게 된다.

이를 일반화해서 data의 차원 수가 많아지게 되면 linear한 케이스로 해결하기 어려울 것이다. 하지만 결국 하고자하는 접근은 비슷하기 때문에 우선은 간단하게 linear decision boundary의 경우를 먼저 이해해보고자 한다. 이렇게 편의성을 위해서 먼저 우리는 dataset이 linearly seperable하다는 가정을 할 것이다. 이렇게 가정한다는 것은 결국 data를 linear decision boundary를 통해서 나눈다고 했을 때 error가 0이어야 한다는 것을 의미한다. Non-trivial 케이스의 경우는 error가 존재할 것이기에 이후에 알아볼 것이다.

그래서 다시 우리가 찾고자 하는 것은 다음을 만족하는 $w$ 이다. 만약 위에서 본 것과 같이 $\lambda$ 를 고려하게 된다면 문제를 해결하기 어려울 것이다. 그래서 $(w,b)$ 에 하나의 constraint를 설정하여 optimal parameter를 unique하게 만들 것이다. 그래서 optimality를 해치지않는 하나의 cosntraint로 canonical hyperplane이 존재한다. Canonical hyperplane이라는 것은 $|w^Tx_i+b|$ 라는 function이 1이어야 한다는 것이다.

\operatorname*{min}_i |w^Tx_i+b| = 1

이렇게 하면 결국에 optimization이 더 쉬워지고, objective function이 다음과 같이 하나로 정해지게 될 것이다.

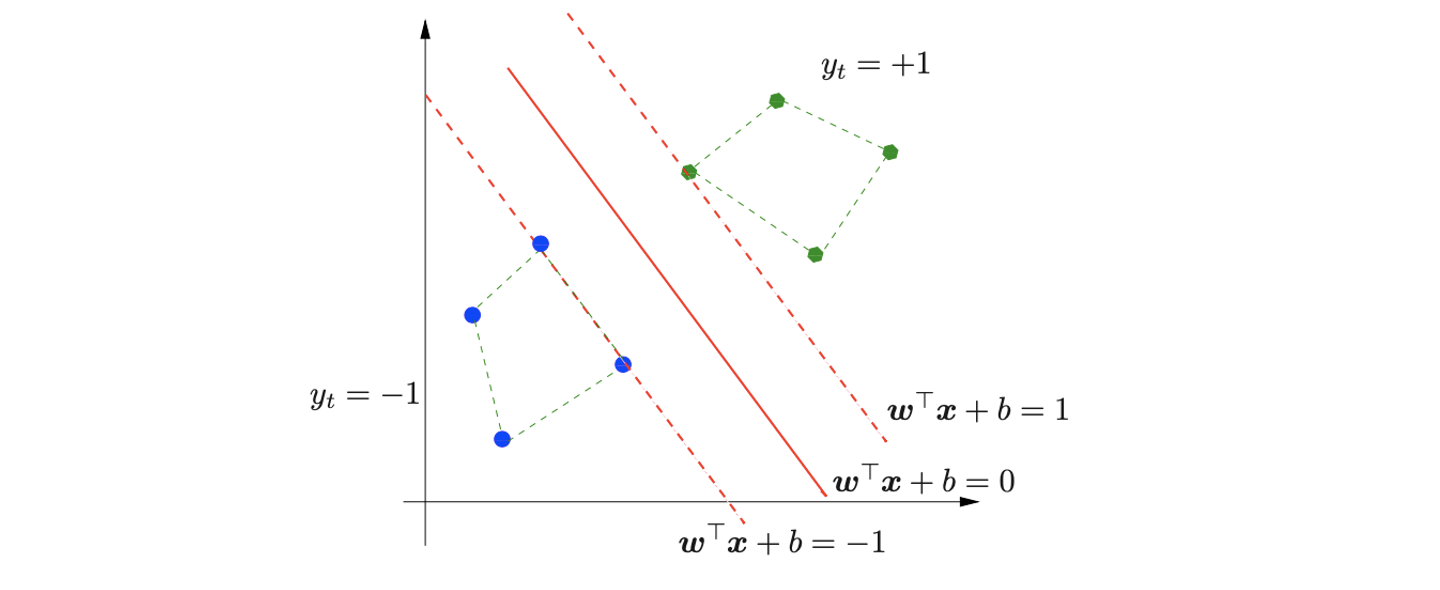\operatorname*{max}_w \frac{1}{||w||} \qquad \text{s.t } \operatorname*{min}_i |w^Tx_i+b| = 1

Graphical illustration을 통해서 우리가 결국에 하고자 하는 것을 보면 우리가 찾고자 하는 것은 hyperplane $w^Tx+b=0$ 이고, 이에 대해서 constraint를 1로 줬을 때 그 지점에 해당하는 data point가 존재할 것이다. 이를 support vector라고 하며, 결국 optimal classifier를 찾는다는 것은 support vector를 찾는 것과 같은 의미가 된다.

Canonical hyperplane을 통해서 형식적으로 margin을 최대로 만드는 문제는 다음과 같이 minimization problem으로 다시 나타낼 수 있다.

\operatorname*{minimize}_{w,b}\quad \frac{1}{2}||w||^2_2

\text{subject to }\quad y_i(w^Tx_i+b)\geq1 \; \quad\forall i=1,\dots,N

그리고 이러한 constraint가 등장하게 된 배경은 지금까지 살펴본 내용들을 정리해보면 이해할 수 있다.

\operatorname*{max}_w \operatorname*{min}_i \frac{f(x_i)}{||w||} \Rightarrow \operatorname*{max}_w \frac{1}{||w||} \;\text{s.t } \operatorname*{min}_i |w^Tx_i+b| = 1

이렇게 optimal $w$ 를 unique하게 하기 위해서 canonical hyperplane을 정의했고, 결국 이를 만족시켜야 하기 때문에 위와 같이 constraint를 정의한 것이다. 결국 equality constraint를 inequality constraint로 바꾸고 싶은 것이다.

\operatorname*{min}_i |w^Tx_i+b| = 1 \Rightarrow y_i(w^Tx_i+b)\geq1 \; \quad\forall i=1,\dots,N

이를 graphical illustrationt을 통해서 이해해보면 data point가 class +1에 해당하는 경우의 초록점들이라면 classification region을 $w^Tx+b=1$ 을 통해서 나눠야 하고, data point가 class -1에 해당하는 경우의 파란점이라면 classification region을 $w^Tx+b=-1$ 을 통해 나눠야 한다. 이러한 관점은 다음과 같이 geometric margin을 수식으로도 변환시킬 수 있다.

\rho = \frac{1}{2}\{\frac{f(x^{+})}{||w||}-\frac{f(x^{-})}{||w||}\}

=\frac{1}{2}\frac{1}{||w||}\underbrace{\{w^Tx^+-w^Tx^-\}}_{2}=\frac{1}{||w||}

$x^+,x^-$ 는 constraint가 주어진 hyperplane과 처음으로 만나는 support vector를 의미한다. 이렇게 양쪽의 support vector를 찾게되면 쉽게 margin을 최대로 만드는 optimal hyperplane을 찾을 수 있다는 것이다. 다시 말해서 모든 data point에 대해 기존의 constraint $\operatorname*{min}_i |w^Tx_i+b| = 1$ 는 $y_i(w^Tx_i+b)\geq1$ 로 바꾸어 나타낼 수 있게 되는 것이고, objective function이 maximization margin에서 minimization으로 바뀐 이유는 단순히 분자와 분모를 바꾸어 기존의 margin을 최대로 했어야 했다면 바꾼 후에는 최소로 만들어야 하기 때문이다. 그리고 기존의 margin에 대해서 편의성을 위해서 squared L2-norm으로 바꾸고 2로 나누어줬다.

이러한 optimization problem의 solution을 binary Support Vector Machine(SVM) 이라고 하며, optimization problem을 풀기 위해서는 gradient-based method 등을 사용하면 된다. 그러나 이렇게 constraint가 존재하는 경우에는 기존의 GD 등의 사용이 불가능하다. 기존의 gradient-based method같은 경우 unconstrained optimization problem에 적용이 가능했기에 지금부터는 이러한 constrained optimization problem을 해결하는 방법에 대해서 알아볼 것이다.

Understanding Constraint Optimization and Duality

Constrained Optimization Problem

Constrained optimization problem은 일반적으로 다음과 같이 loss function을 minimization 하도록 되어있다.

\operatorname*{min}_x\quad L(x)

\text{subject to}\quad g_i(x)\leq0 \quad\forall i=1,\dots,m \quad \text{where }g_i: \mathbb{R}^D\rightarrow\mathbb{R}

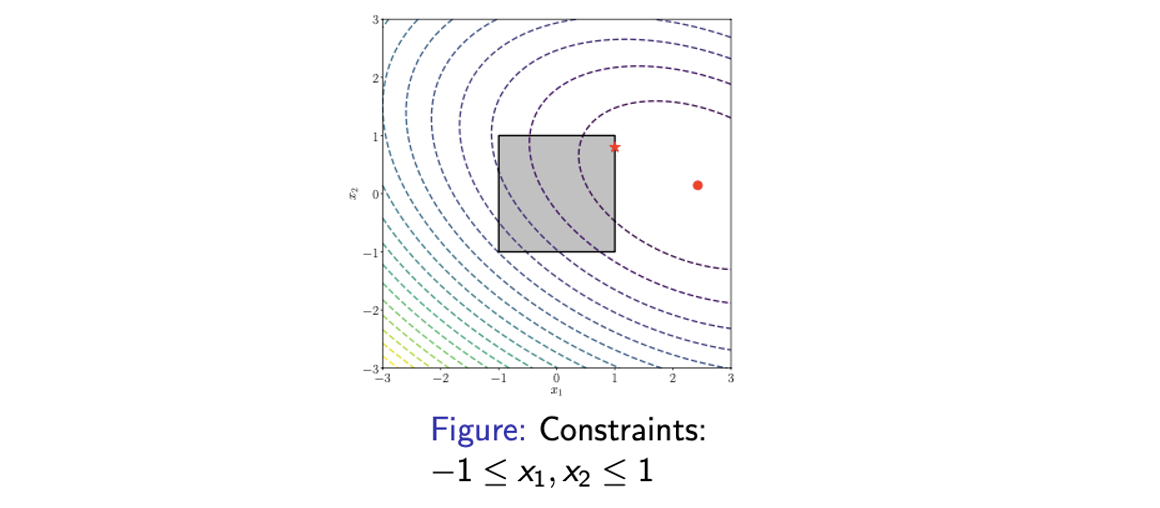이러한 구조는 SVM problem에 대응시킬 수 있다. $x$ 는 $w,b$ 로 대응되고 constraint $g_i(x)\leq0$ 은 $y_i(w^Tx_i+b)\geq1$ 과 대응이 된다. Constraint가 달라보여도 식을 한쪽으로 이동시키면 $1-y_i(w^Tx_i+b)\leq0$ 과 같이 되어 결국 같은 형태가 된다. 그리고 우리는 이러한 constrained minimization problem을 primal problem이라고 한다.

From Constrained to Unconstrained

앞서 이야기 했듯이 이러한 constrained optimization problem은 바로 풀 수가 없다. 그러나 unconstrained optimization problem의 경우는 어떻게 풀어야 하는지 이미 알고 있을 것이다. GD나 Newton's method 등을 사용해서 풀 수가 있기 때문에 우리는 일종의 penalty function을 추가해서 constrained optimization problem을 unconstrained optimization problem으로 변환해서 풀고자 한다. Primal problem의 $L(x)$ 를 그냥 minimization 하기 보다는 penalty function을 추가해서 $J(x)$ 를 다음과 같이 정의할 것이다.

J(x) = L(x)+\underbrace{\sum_{i=1}^m 1(g_i(x))}_{\text{penalty function}}

여기서 penalty function은 infinite step function으로 되어 있으며 다음과 같이 정의되어져 있다. 이 식은 constraint를 위반하는 경우에 대해서 $\infty$ 라는 penalty를 주고자 하는 것이다. 그러나 만약 대응되는 inequality가 입증이 된다면 penalty를 주지 않는 구조이다.

1(z)=\begin{cases}0 & \text{if }z\leq0\\\infty & \text{otherwise}\end{cases}

이렇게 $J(x)$ 를 정의하고 minimization problem을 풀어도 primal problem의 해는 동일하게 된다. 그러나 아쉽게도 아직은 알려진 방법들로 문제를 해결할 수 없다. 이러한 penalty function의 경우 많은 곳에서 0 gradient를 가지고 있고, 이러한 $\infty$ penalty는 현실에서는 존재하지 않기 때문이다.

Lagrangian Dual

따라서 사람들은 이를 해결하기 위해서 Lagrangian dual method라는 것을 생각해냈다. Lagrangian dual method를 설명하기 위해서 먼저 Lagrangian function이 무엇인지 정의해보고자 한다. Lagrangian function $\mathcal{L}$ 은 다음과 같이 variable $x$ 와 Lagrangian multiplier vector $\lambda$ 의 function이다. Constraint를 $m$ 개라고 가정하는 상황이다.

\mathcal{L}(x,\lambda)=L(x)+\underbrace{\sum_{i=1}\lambda_ig_i(x)}_{\text{differentiable, non-zero}} \qquad\text{ where }\lambda=[\lambda_1,\dots,\lambda_m]^T

이러한 구조는 위에서 살펴본 $J(x)$ 와 매우 유사하지만, 차이점은 Lagrangian multiplier의 항이 미분이 가능하고 non-zero 값을 가진다는 것이다. 이렇게 Lagrangian function을 정의하고나면 기존의 primal problem에 대한 Lagrangian dual은 다음과 같이 정의할 수 있다.

\operatorname*{max}_{\lambda\in\mathbb{R}^d} \quad \mathcal{D}(\lambda)

\text{subject to }\quad \lambda \geq 0 \quad

\text{ where }\mathcal{D}(\lambda)=\operatorname{min}_{x\in\mathbb{R}^d}\mathcal{L}(x,\lambda)

결국 다음과 같이 정리할 수 있다.

\operatorname*{max}_{\lambda\geq0}\underbrace{\operatorname*{min}_x \mathcal{L}(x,\lambda)}_{\text{unconstrained}}

결국 이렇게 Lagrangian dual을 사용하면 기존의 풀 수 없었던 primal problem을 unconstrained optimization problem으로 바꿀 수 있고, 이를 dual problem이라고 한다.

Minimax Inequality

Primal problem을 dual problem으로 바꾸게 되면 흥미로운 성질을 발견할 수 있게 된다. 바로 max min function을 동일한 function의 min max problem으로 upper bound를 설정할 수 있게 된다. 그리고 이를 minimax inequality라고 한다.

\operatorname*{max}_y \operatorname*{min}_x \rho(x,y) \leq \operatorname*{min}_x \operatorname*{max}_y \rho(x,y)

이를 증명하는 과정은 간단하면서도 흥미롭다.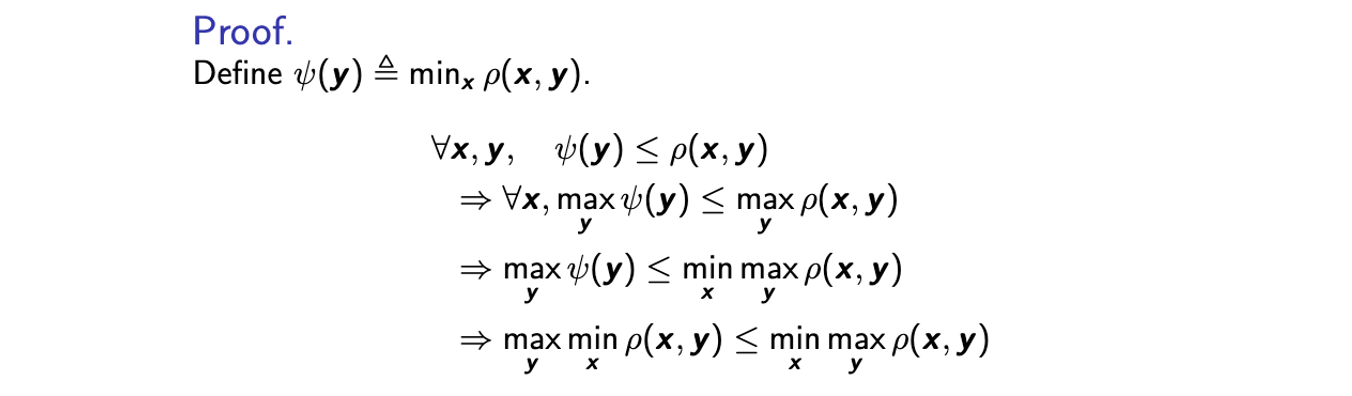 $\psi(y)$ 를 $\operatorname{min}_x \rho(x,y)$ 이라고 정의했을 때 임의의 $x,y$ 에 대해서 $\psi(y)$ 는 $\rho(x,y)$ 의 lower bound가 될 것이다. 이러한 정의는 임의의 $y$ 에 대해서 만족하기 때문에 각각을 $y$ 에 대해서 maximization 할 수 있다. 그리고 또한 이는 임의의 $x$ 에 대해서도 만족하기 때문에 $x$ 에 대해서 각각을 minimization 할 수 있다. 그리고 마지막에 $\psi(y)$ 의 정의를 대입해주면 minimax inequality가 증명이 끝났다.

Weak Duality with Minimax Inequality

이제 minimax inequality를 $J(x)$ 와 $\mathcal{L}(x,\lambda)$ 에 적용해보고자 한다. 그래서 먼저 $J(x)$ 를 다음과 같이 정의할 것이다.

J(x)=\operatorname*{max}_{\lambda\geq0}\mathcal{L}(x,\lambda) \qquad \text{ where } \mathcal{L}(x,\lambda)=L(x)+\sum_{i=1}^m\lambda_ig_i(x)

Primal problem을 다시 생각해보면 $L(x)$ 의 $g_i(x)\leq 0$ 이라는 constraint를 가지는 minimization problem이었다. 그리고 $\lambda_i$ 가 0 이상이고 $g_i(x)$ 는 0 이하라면 $\mathcal{L}$ 의 두번째 항은 음의 항이 되고 기존의 primal problem에서는 $L(x)$ 를 최소로 만들고자 하여 다음과 같은 식을 만족할 것이다. 즉, Primal problem의 목적으로 인해 다음과 같이 $J(x)$ 를 최소한으로 만들고자 할 것이다.

\operatorname*{min}_x J(x)=\operatorname*{min}_x \operatorname*{max}_{\lambda\geq0} \mathcal{L}(x,\lambda)

결과적으로 minimax inequality를 통해 다음과 같이 primal solution과 dual solution 사이의 inequality를 얻을 수 있다.

\underbrace{\operatorname*{min}_x\operatorname*{max}_{\lambda\geq0}\mathcal{L}(x,\lambda)}_{\text{Primal solution}}\geq\underbrace{\operatorname*{max}_{\lambda\geq0}\operatorname*{min}_x\mathcal{L}(x,\lambda)}_{\text{Dual solution}}

Primal solution에서의 min과 max를 dual solution에서는 위치를 바꾸게 된 것이다. 따라서 Lagrangian dual을 최대로 만들게 되면 우리는 primal solution의 lower bound를 얻게 되는 것이고, 이를 weak duality라고 한다. Primal problem에서 minimization에 초점을 맞췄다면, dual problem에서는 maximization에 초점을 맞춰서 lower bound를 얻을 것이다.

Why Dual?

Dual form을 사용하는 이유는 다음과 같이 unconstrained optimization problem이 우변의 안쪽 부분에 생기기 때문에 이제는 GD 등의 method를 이용할 수 있게 된다.

\operatorname*{min}_x\operatorname*{max}_{\lambda\geq0}\mathcal{L}(x,\lambda)\geq\operatorname*{max}_{\lambda\geq0}\underbrace{\operatorname*{min}_x\mathcal{L}(x,\lambda)}_{\text{unconstrained}}

그러나 이렇게 하면 constraint를 위반하게되는 risk가 생기게 되어 equality를 만족하는 primal보다 더 작은 loss 값을 가지게 될지도 모른다. 그러나 대부분의 경우에는 equality를 만족하게 된다.

Equality Constraints

Equality constraint $h(x)=0$ 는 다음과 같이 2개의 inequality를 만족하면 된다.

h(x)\leq 0

h(x)\geq 0

이러한 개념을 Lagrangian dual에서 오직 inequality constraint에만 적용시키면 Lagrangian dual의 결과를 다음과 같이 만들 수가 있다.

\mathcal{L}(x,\lambda)=L(x)-\lambda h(x), \qquad \lambda\in\mathbb{R}

With Equality Constraints

그러면 다음과 같이 inequality constraint와 equality constraint가 있는 primal problem이 있다고 생각했을 때, Lagrangian은 다음과 같이 만들어진다.

$\text{General primal problem:}$

\operatorname*{minimize} \quad \mathcal{J}(w)

\text{subject to} \quad g_i(w)\leq 0, \quad i=1,\dots,M

\quad \quad \quad \quad \quad h_j(w)=0, \quad j=1,\dots,L

$\text{Lagrangian:}$

\mathcal{L}(w,\nu,\lambda)=\mathcal{J}(w)+\sum_{i=1}^M\nu_ig_i(w)+\sum_{j=1}^L\lambda_jh_j(w)

\text{where } \nu_i > 0 \text{ for } i=1,\dots,M \text{ and }j = 1,\dots,L

Karush-Kuhn-Tucker(KKT) Necessary Condition

이러한 Lagrangian의 일반적인 형태를 기반으로 Lagrangian dual와 primal의 equality를 만족시키기 위한 필수적인 조건들이 존재하고, 이를 KKT necessary condition이라 한다. 이러한 condition은 primal problem에서 $w$ 를 solution으로 보장하게 된다. $w$ 를 primal problem의 solution이라고 했을 때 다음의 3가지 condition들을 만족하게 된다.

1. Optimality

\nabla\mathcal{L}=\nabla\mathcal{J}(w)+\sum_{i=1}^M\nu_i\nabla g_i(w)+\sum_{j=1}^L\lambda_j\nabla h_j(w)=0

Optimality같은 경우 $\mathcal{L}$ 을 $w$ 에 대해서 gradient를 구해주면 0인 지점에서 optimal solution이 보장이 된다는 것이다.

2. Feasibility(Primal Constraints)

g_i(w) \leq 0, \quad \forall i=1,\dots,M

h_j(w) = 0, \quad \forall j=1,\dots,L

Feasibility의 경우 $w$ 가 optimal solution이라면 당연히 만족해야 하는 condition이다.

3. Complementary Slackness

\nu_ig_i(w)=0,\quad \forall i=1,\dots,M\; (\nu_i >0)

Complementary slackness는 inequality constraint에서 추가되는 condition으로, non-trivial하지만 $\nu_i$ 가 양수면 만족하게 된다. 이 condition은 SVM solution의 derivate에 사용이 되어 식을 정리할 때 사용될 것이다. $\nu_i >0$ 이라는 것은 $\mathcal{L}(w,\nu,\lambda)$ 에서의 $\nu_i$ 가 maximization에서는 계속해서 감소한다는 것을 의미한다. 왜냐하면 $g_i(w)$ 가 양수가 아니기 때문이다.

\nu_i >0 \Leftrightarrow g_i(w)=0

\nu_i=0 \Leftrightarrow g_i(w)< 0

Optimal solution $w$ 가 $g_i(w)<0$ 의 경우에는 어떠한 영향을 받지 않아서 $\nu_i$ 가 0으로 주어지게 된다. 만약 $w$ 가 $g_i(w)=0$ 의 경우라면 이는 equality constraint과 같아지게 된다. $\nu_i$ 는 constraint에서 최적화 되고 $g_i$ 도 다른 constraint에서 최적화 되어 2개의 inequality는 동시에 slack이 존재하지 않게 된다. Inequality에서 slackness라는 것은 complementary이고, 만약 $g_i$ 에 slackness가 없다면 $\nu_i$ 가 slack을 가지게 되고 반대로 slack이 $g_i$ 에 있다면 $\nu_i$ 에는 slackness가 없다는 것이다.