[데이터마이닝] Evaluating Machine Learning Methods 2

Confusion Matrices / Contingency Tables

Training과 test를 진행할 때 우리는 model에 training set을 이용해서 학습시킨 뒤에 test set을 이용해서 성능을 평가하려고 하다보면 다음과 같은 matrix를 얻을 수 있을 것이다. 그리고 우리는 이를 confusion matrix 혹은 contingency table이라고 부를 것이다.
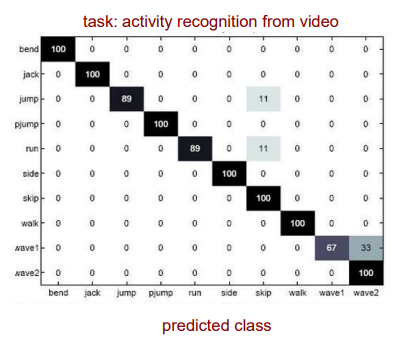위의 matrix가 이야기하고자 하는 것은 무엇일까? 우선 위의 예시는 activity recognition에서 possible class label들과 predicted class label들에 대한 confusion matrix이다. 우선 diagonal element를 보면 대부분 높은 값들을 가지고 있는 것을 볼 수 있다. 총 1000개의 test data가 있는 것이고, 각 class마다 100개씩 해당하고 있는 것이다. 그래서 diagonal element가 말하는 것은 우리의 model이 정확하게 몇개의 sample을 맞췄는지를 의미한다. 100이면 100개 중에 사실상 전부 다 맞게 예측한 것이다. Jump를 보게 되면 총 100개 중에 89개를 정확하게 맞춘 것이고 11개를 틀린 것이다. 그래서 off-diagonal element들은 전부 잘못된 classification 결과를 이야기하는 것과 같다.

Confusion Matrix for 2-Class Problems

위의 예시는 10개의 class이지만 이번에는 간단한게 binary class에 대한 confusion matrix를 알아볼 것이다. 다음은 2-class problem에 대한 confusion matrix이다.
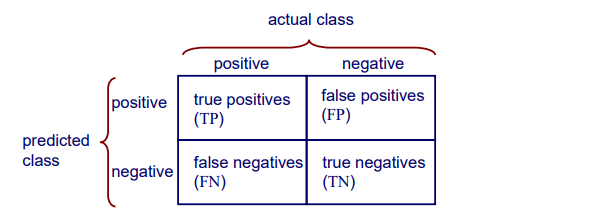Class는 positive class와 negative class로 나누고 binary case이기 때문에 총 4개의 경우가 존재할 것이다. 각 class에 대해서 맞고 틀리고하면 총 4가지 경우가 존재한다. 그리고 우리는 각 상황을 다음과 같이 정의한다.

True positive(TP) : Actual - positive / Predicted - positive
False positive(FP) : Actual - negative / Predicted - positive
True negative(TN) : Actual - negative / Predicted - negative
False negative(FN) : Actual - positive / Predicted - negative

True와 false는 actual class와 predicted class가 동일한 경우에 대해서 말하는 것이다. 사실은 $2\times 2$ matrix라 단순해보이지만 기존의 원칙은 그대로 유지하고 있다. Diagonal element는 올바르게 classification한 결과를 나타내고 있고, off-diagonal element는 잘못된 classification 결과를 보여주는 것이다.

Is Accuracy Perfect? No!

Accuracy는 사람들이 가장 흔하게 사용하는 measure 중 하나이다. 여기서 의문점은 항상 accuracy가 완벽할 수 있는지이다. Accuracy가 자주 사용되기는 하지만 accuracy를 사용하면 안되는 경우들이 존재한다.

1. There is a large class skew
Class skew가 큰 경우에는 유용하지 못할 것이다. 만약 1000명의 사람들 중에 30명이 cancer를 가지고 있고 나머지 970명이 정상이라고 해보자. 그리고 이러한 data에 대해서 model을 디자인한다고 했을 때, 새로운 data가 들어왔을 때 정상이라고 알려주도록 만들고 싶다. 그러면 이 model은 이미 data만 봤을 때 97%의 accuracy를 보일 것이다. 그래서 이렇게 class skew가 큰 경우에는 accuracy가 의미가 없을 것이다. 오히려 30명의 암 환자를 classification하는 것이 더 의미있을 것이다.

2. There are differential misclassification costs - getting a positive wrong costs more than getting a negative wrong
Cancer 환자를 잘못 classification하면 실제로는 큰 일이 발생할 것이다. 하지만, 정상인 사람을 잘못 classification하게 된다면 사실 classification 입장에서는 아쉬울 순 있지만 실제로는 큰 일이 발생하지는 않을 것이다. False positive로 인해 외부 검사가 발생하지만 false negative로 인해 질병을 치료하지 못하는 medical 영역을 고려해보면 이는 중요한 문제일 것이다.

3. We are most interested in a subset of high-confidence predictions
아마 어떠한 경우에는 classification을 잘못했다고 하더라도 이를 남겨둬도 괜찮을지도 모른다.

Other Performance Metrics 1 - TPR(Recall) and FPR

이러한 issue들 때문에 또 다른 metric이 필요할지도 모른다. 그래서 이번에는 accuracy와는 조금 다른 metric들에 대해서 알아보려고 한다.

True positive rate(recall)는 실제로 positive인 class들에 대해서 model이 얼마나 정확하게 예측했는지를 비율로 나타낸 것이다. 반대로 false positive rate의 경우에는 실제로 negative인 class들에 대해서 model이 얼마나 positive라고 예측했는지를 비율로 나타낸 것이다. 우리는 true positive rate를 최대한 높이면서 false positive rate를 최대한 낮추기를 원한다.

ROC Curve

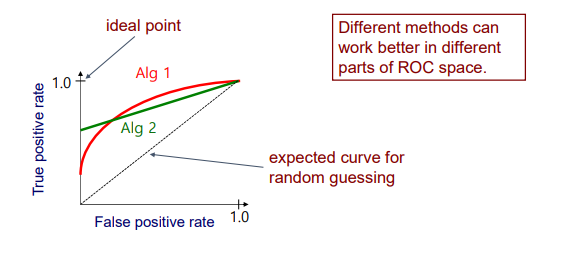Receiver Operating Characteristic(ROC) curve는 true positive rate와 false positive rate에 대한 curve이다. ROC curve는 positive의 instance가 변화하는 confidence에 대한 threshold 값으로 TP-rate와 FP-rate를 그려나간다. 위의 그림에서 false positive rate가 0인 지점에서 true positive rate가 100%인 지점인 ideal point가 있다. 하지만 실제로 이 지점에 도달하는 것은 잘 일어나지 않을 것이다. True positive rate가 100%라는 이야기는 모든 instance들에 대해서 전부 올바르게 classification했다는 것이기 때문이다. 실제로는 위와 같이 red curve나 green curve와 같이 ROC curve가 형성될 것이다. 만약 대각선으로 형성이 된다면 50:50이기 때문에 모든 결과가 random일 것이다. 그리고 ROC curve의 모양을 결정하는 것은 어떠한 method를 사용했는지에 따라 달라지게 된다. 그렇기 때문에 매 지점마다 더 잘 동작하는 method가 전부 다를 것이다.

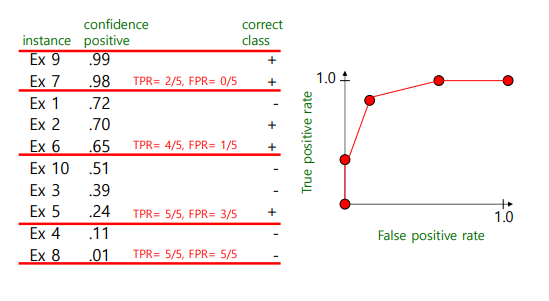실제로는 confidence positive에 따라서 sorting을 한 뒤에 적절하게 threshold에 따라서 그 지점에서의 TPR과 FPR을 보고 ROC curve를 그려나가는 것이다.

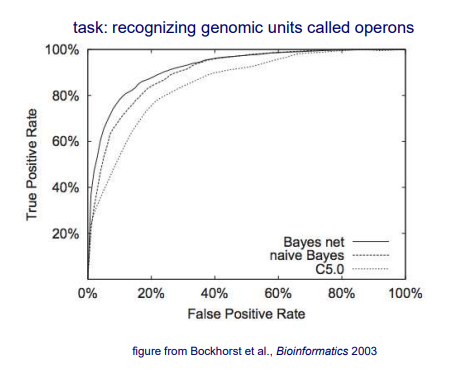그리고 위는 실험을 통해서 여러 method에 따라 실제로 ROC curve를 보여주는 예시이다. Binary classification을 하기 위해서 3가지의 classfier를 이용한 실험의 결과이다. C5.0는 decistion tree이고 Bayes net은 naive Bayse classifier의 일종으로 어느정도 확장된 classifier이다. 위의 curve를 보면 Bayes net이 다른 2가지보다 더 위에 있는 것을 볼 수 있다. 그렇기 때문에 이 classifier가 가장 좋은 성능을 냈다고 이야기할 수 있다.

사람들은 이 curve를 보고 FPR을 기준으로 AUC를 계산해서 그 성능을 확인할 수 있다. AUC는 Area Under Curve로 curve의 아래 면적의 넓이를 나타내는데, Bayes net의 경우 다른 method보다도 더 넓은 면적을 보이고 있는 것을 확인할 수 있다. 그리고 AUC의 최대값은 1이고 값이 크면 클수록 더 선호하게 되는 것이다.

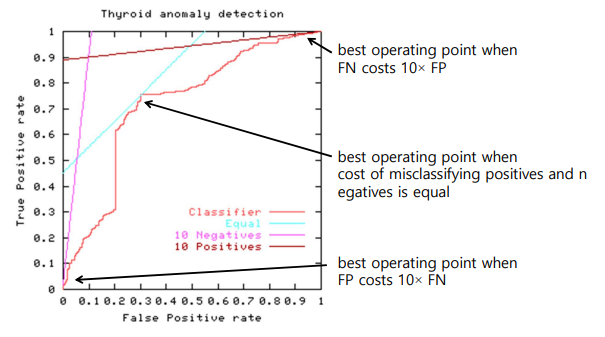Best operating point는 FN 및 FP의 misclassification의 상대적인 cost에 따라 달라진다. 무슨 의미인지 알아보기 위해서 먼저 위의 red curve를 보도록 하겠다. Smooth하지는 않지만 어느정도 trend를 파악할 수 있는 상태이다. 만약 positive와 negative가 1:1의 비율이라면 curve는 기울기가 1인 직선 상태로 존재할 것이다. 그렇기 때문에 동일한 직선의 경우 classifier의 결과와 만나는 지점이 아무래도 best option이 될 것이다. 만약 false negative가 false positive보다 10배의 비율로 존재한다면, 위에서는 10 Positives라는 기울기가 매우 작은 직선으로 존재할 것이고 이 직선과 classfier가 만나는 지점이 best option이 될 것이다. 반대로 false positivie가 false negative보다 10배의 비율로 존재한다면, 위에서는 10 Negatives라는 기울기가 매우 큰 직선으로 존재할 것이고 이 직선과 classfier가 만나는 지점이 best option이 될 것이다. 이 경우에 우리는 positive인 것들을 놓치기 싫다는 것이다. Positive sample들을 negative sample들에 비해서 놓치기 싫다는 입장인 것이다.

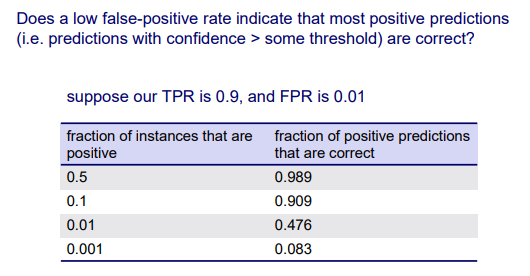낮은 FPR이 대부분의 positive prediction이 정확하다는 것을 의미하는 것일까? 예를 들어 TPR이 0.9이고 FPR이 0.01이라고 해보자. 이 경우에 ROC curve를 그리게 되면 정말로 훌륭한 ROC curve를 그릴 수 있을 것이다. 하지만 이것은 또한 오해의 소지를 불러일으킬 수 있다.

만약 data set에 positive class를 가지는 sample이 50%가 있는 경우에는 TPR의 값이 상대적으로 높게 나올 것이다. 하지만 data set에 positive class를 가지는 sample이 정말 낮은 경우에는 비록 TRP이 정말 높다고 하더라도 positive prediction은 좋지 못할 것이다. 만약 dataset이 500:500으로 균형이 잡혀있다면, 0.9 TPR과 0.01 FPR의 경우에는 positive prediction 중에서 알맞게 classification한 결과가 대략 99%나 될 것이다. 이는 꽤 좋은 결과이다. 하지만 1%의 positive인 data에서 예를 들어 30:2970이라면, 이 positive instance의 fraction이 정말 작다면 FPR이 낮다고 해서 반드시 positive로 분류되는 것은 아닐 것이다. 이 예시에서는 30개 중에 약 15개 정도만이 올바르게 classification 될 것이다. 그래서 TPR과 FPR이 최선의 선택은 아니다. 즉, 낮은 FPR이 우리의 prediction 결과가 좋다고 무조건 이야기하는 것은 아니다. 결론적으로 우리는 TPR와 FPR을 함께 보고 고려해야 한다.

Other Performance Metrics 2 - Precision

그래서 이번에는 또 다른 metric을 알아보려고 한다. TPR과 FPR이 최선의 선택이 아니기 때문에 이번에는 positive sample들뿐만 아니라 FP도 함께 고려해보려고 한다. 우리는 이러한 것을 precision을 통해서 살펴볼 것이다.

FPR은 negative sample들만을 이용해서 FP의 비율을 알아본 것이었다. Precision에서는 우리가 positive라고 예측한 결과를 통해서 실제 TP의 비율을 확인하고자 하는 것이다. TPR은 recall로도 불리며 이는 실제로 positive인 sample에 초점을 맞췄다. 여기서 precision은 우리의 예측이 positive인 sample들에 초점을 맞추겠다는 것이다.

만약 30명의 cancer 환자(positive)들이 있다면, recall은 이 중에서 얼마나 많은 환자들을 cancer 환자로 분류했는지이다. 반면, precision은 cancer 환자로 분류한 사람들 중에서 얼마나 많은 환자들이 실제로 cancer 환자인지를 나타내는 것이다. Recall은 실제 cancer 환자들을 모두 다루게 된다. Precision은 얼마나 우리의 예측이 정확한지를 나타낸다.

Precision / Recall Curve

그래서 지금부터는 recall과 precision을 이용해서 또 다른 curve를 그릴 수 있다. 우리는 이를 precision/recall curve(PR curve)라고 부른다. 이 curve를 그리게 되면 다음과 같이 우하향하는 curve를 볼 수 있다.
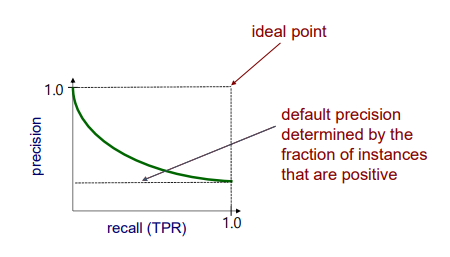PR curve에서 minimum 값이 의미하는 것은 positive instance가 차지하는 비율에 의해 결정되는 기본 precision이다. 즉, 우리의 precision이 이 값 밑으로는 절대 내려갈 수 없다는 것이다. 그리고 PR curve의 ideal point는 이번에는 우측 상단에 존재할 것이다. 우리의 precision을 최대한 높이고 싶다면, 동시에 recall도 높은 값을 유지해야 한다. 그러나 현실에서는 잘 일어나지 않는 상황이다. 그리고 다음은 실제로 PR curve를 실험을 통해서 얻은 결과이다.

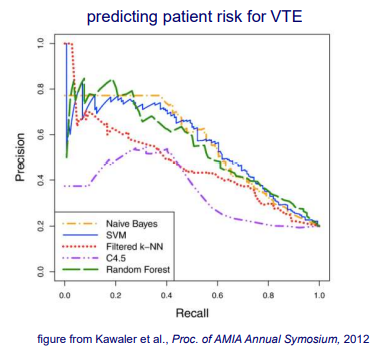다시 이 curve를 기반으로 서로 다른 method들을 비교하기 위해서 AUC를 계산할 수 있을 것이다. 아마 위에서는 C4.5 algorithm이 가장 좋지 못한 성능을 보일 것이다. 나머지는 비슷한 경향을 보이기 때문에 AUC를 계산해서 비교할 필요가 있다.

How do we get one ROC / PR Curve when we do CV?

그렇다면 cross validation을 통해서는 어떻게 ROC curve나 RP curve를 얻을 수 있을까? CV나 random resampling을 한다고 했을 때, 우리는 여러번의 training과 testing을 구성하게 된다. 하나의 curve를 얻기 위한 하나의 방법으로는 먼저 fold에 걸쳐서 confidence value들을 비교할 수 있다는 가정이 필요하다. 각각의 test set을 사용한다고 하더라도 동등하게 비교가 가능한 조건이어야 한다. CV의 장점은 아무래도 전체 dataset을 test할 수 있다는 것이다. 전체 dataset이 결국에는 한번씩 test 과정에 동반되기 때문이다. 그래서 우리는 모든 test set에서 prediction을 모을 수가 있다. 이는 모든 sample들로부터 prediction 결과를 얻을 수 있어서 이를 기반으로 curve를 그려나갈 수 있다. 또 다른 방법으로는 더 직관적이게 각각의 curve를 그린 다음에 평균을 구하는 것이다. 모든 test set에 대해서 각각의 curve를 그린 다음에 각 curve를 function으로 보고 평균을 구하는 것이다. 이는 첫번째 방법보다도 더 직관적일 것이다.

Comments

ROC / PR Curve

ROC와 PR curve 둘다 prediction performance를 다양한 confidence level에서 평가할 수 있도록 해야한다. 왜냐하면 threshold를 바꿀 수 있기 때문이다. Threshold를 바꾸게 되면 다른 level에서 성능을 평가하게 될 것이다. 또한, 이 curve들은 binary classification task를 기반으로 그려지기 때문에 이러한 가정이 중요하다. 그리고 classfier가 얼마나 잘 동작하는지는 AUC를 계산해서 비교하는 과정을 통해서 확인할 수 있다.

ROC Curve

ROC curve는 class distribution의 변화에 민감하지 않다. Test set에서 positive instance와 negative instance의 비율이 달라지는 경우에는 ROC 곡선이 변하지 않는다. TPR은 실제로 positive에 대해서, FPR은 실제로 negative에 대해서만 고려하기 때문에 서로 영향을 줄 수가 없다. 각각의 instance가 몇개든 중요하지 않다. 그리고 ROC curve는 잘못 분류된 cost 비용이 다른 작업에 대한 최적의 classification threshold를 식별할 수 있다. 왜냐하면 우리는 이 curve를 기반으로 어떠한 threshold를 사용해야할지 선택해야하기 때문이다.

PR Curve

PR curve는 false positive에 대한 prediction의 비율을 보여주게 된다. 그리고 PR curve는 많은 negative instance들에 대한 task에 적합하다. 만약 class label distribution이 한쪽으로 편향되어 있다면, 이를 평가하기 위해서 PR curve를 사용하는 것이 좋을 것이다.