[데이터마이닝] Evaluating Machine Learning Methods 1

지금까지 decision tree나 Naive Bayes classfier와 같이 여러 classifier들에 대해서 알아보았다. 그리고 우리는 이러한 model들이 충분히 학습이 되었는지 확인할 필요가 있다. 그래서 이번에는 classifier와 같이 model들을 학습을 시킨 후에 얼마나 잘 동작하는지 확인하는 evaluation 과정에 대해서 알아보려고 한다.

Bias of an estimator

가장 먼저 bias가 무엇인지에 대해서 이야기해보려고 한다. 학습을 하다보면 estimation을 하기 위해서 학습에 사용한 true parameter $\theta$가 있고, 학습이 된 model을 통해서 estimation을 한 prediction parameter $\hat{\theta}$가 있을 것이다. 우리의 목적은 우리의 estimation $\hat{\theta}$가 ture value $\theta$와 거의 같아지기를 원한다. 이 2개의 값이 완전히 같아지면 좋겠지만, 현실적으로 그나마 근사하는 것을 목표로 하고 있다. 이를 위해서 우리의 estimation에 대한 bias를 구하고자 하는 것이다.

$\theta$의 예시로는 model accuracy가 있을 수 있고, $\hat{\theta}$의 예시로는 test set accuracy가 있을 수 있다. 학습이 된 model을 이용해서 test를 하기 때문에 우리는 test할 때의 accuracy가 학습할 때의 accuracy와 같아지기를 원한다. 이는 곧 우리의 model이 특정한 상황에만 잘 동작하는 것을 원하지 않겠다는 것이다. 가장 이상적으로는 우리의 model이 generalizable해지는 것을 목표로 한다. 학습에 사용된 data에만 국한하는 것이 아닌 보지 않은 새로운 data에 대해서도 확장이 가능해지기를 원한다. 그래서 우리의 estimator에 대해서 bias를 정의해보려고 하는 것이다.

가장 대표적인 예시로 Gaussian distribution의 parameter인 $\mu$에 대해서 MLE의 결과를 놓고 생각해보려고 한다. 우리의 model이 추정한 parameter의 expectation을 취해서 true parameter와의 차이를 계산하려고 한다. 여기서 expectation을 취하는 이유는 아무래도 많은 경우의 parameter를 추정하게 될 것인데, 여러번의 시도를 하게 되면 아무래도 이 모든 parameter들이 동일하게 추정되지는 않을 것이다. 그래서 bias의 계산 식은 우리의 estimation 결과의 average를 취해서 그 값과 실제 parameter와의 차이를 계산하겠다는 것이다. 그리고 여기서 Gaussian distribution의 경우 항상 동일한 $\mu$가 등장하기 때문에 average를 구해도 같은 값일 것이다. MLE를 통해 구한 $\mu$의 식은 그저 sample들의 average 값이고, 이는 몇번을 추정한다고 하더라도 같은 결과를 보일 것이기 때문이다. 그렇기 때문에 Gaussian distribution에서의 bias는 0가 되어 unbiased estimator가 될 것이다.

Test Sets

Gaussian distribution에서 unbiased estimator에 대해서 알아보았지만, 사실상 대부분 bias가 존재할 것이다. 그렇기 때문에 일반적으로 bias를 줄이기 위해서는 unbiased estimation을 할 수 있어야 하고, 가장 대표적인 방법으로는 가지고 있는 전체 data를 training set과 test set으로 나누는 것이다. 그래서 training set을 이용해서 model을 학습시키고 test set을 이용해서 학습시킨 model로부터 accuracy를 측정하는 것이다.
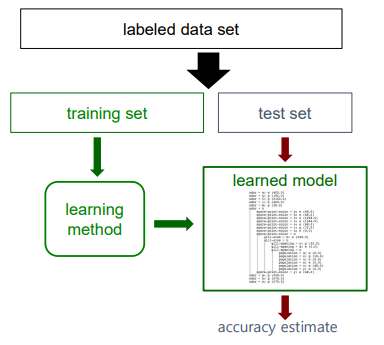이 과정 속에서 우리는 2개의 accuracy를 얻게 될 것이다. 하나는 training accuracy이고 다른 하나는 test accuracy일 것이다. 그리고 우리는 이 2개의 accuracy가 최대한 같아지기를 원한다. 그리고 이러한 경우를 우리는 unbiased estimation이라고 부르는 것이다. Training accuracy와 test accuracy가 동일해지는 것이 unbiased estimation을 보장하게 되는 경우이다. 만약 이 2개의 결과가 완전히 다르다면, 이는 곧 우리의 model이 오로지 training data에만 잘 동작한다는 것을 의미하게 된다. 이는 원하지 않은 결과이기 때문에 model이 generalizable해져서 처음 보는 data set에도 잘 동작하게 만들어야 한다.

우리가 model을 학습시킬 때에는 test data가 아직은 없다고 생각하고 진행해야 한다. 만약 test set의 label들이 학습된 model에 어떠한 방식으로든 영향을 끼친다면, accuracy estimation은 biased 될 것이다. 이는 아무래도 model이 cheating을 하는 것과 같아지기 때문이다. 원래라면 test set이 학습 과정에서는 어떠한 영향도 제공해서는 안된다. Training set과 test set은 완전히 독립적이어야 하고, 여기서 test set은 어떠한 방식으로도 학습 과정에 개입되어서는 안된다.

Learning Curves

다음과 같이 sample size에 따른 accuracy가 plot되어 있는 learning curve에 대해서 알아보도록 하자. 전체 data를 나누어 training set과 test set으로 한다고 했을 때 일반적으로는 더 많은 쪽을 training set으로 선택하곤 한다. 그 이유는 model을 학습시킬 때 model에 parameter의 개수가 많으면 많을수록 충분한 estimation을 위해서는 이에 따라 충분한 개수의 sample이 필요해지게 된다.
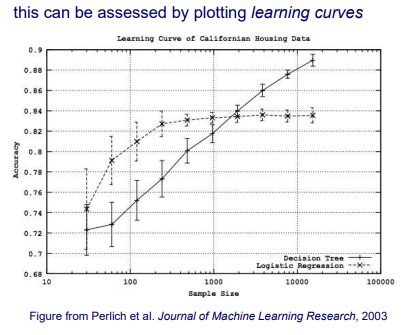그렇다면 training set의 크기에 따라 training method의 accuracy는 어떻게 달라질까? 위의 그래프는 2개의 prediction algorithm인 decision tree와 logistic regression을 보여주고 있다. Sample의 양이 증가하는 초반에는 확실히 accuracy가 크게 증가하는 것을 볼 수 있다. 하지만 logistic regression의 경우 sample의 개수가 1000개 정도부터는 그 양이 많아진다고 해도 accuracy의 상승 폭이 그리 크지 않은 것을 볼 수 있다. 그래서 위의 그래프를 보게 되면 sample의 개수가 적은 경우에는 logistic regression이 훨씬 더 높은 accuracy를 보여주고 있으며, 반대로 sample의 수가 충분히 많은 경우에는 반대로 decision tree가 더 좋은 accuracy를 보여주고 있다.

그렇다면 실제로는 어떻게 learning curve가 그려지는 것일까? 위의 그래프를 보면 sample의 특정 개수마다 위아래로 confidence가 함께 표시되어 있는 것을 볼 수 있다. Learning curve를 그리기 위해서는 training set과 test set이 주어졌을 때, 방금 이야기한 sample의 특정 개수인 $s$마다 무작위로 $s$개의 instance들을 training set으로부터 선택할 것이다. 그리고는 decision tree나 logistic regression과 같은 model을 학습시킨 후에 test set을 이용해서 model로부터 accuracy $a$를 결정할 것이다. 그렇게 해서 해당 sample 수 지점에 accuracy $a$를 표시한 뒤에 이 과정을 여러번 반복해서 여러개의 curve를 만들어낼 것이다. 비슷하지만 약간은 다른 여러 curve들이 그려질 것이고, 이들의 average를 계산하여 최종 curve를 구하고 추가적으로 standard deviation을 계산해 confidence level을 위와 같이 표시해주면 된다. 그래서 사실 특정 훈련 과정에서 운이 좋으면 해당 지점에서 굉장히 좋은 accuracy를 얻을 것이다. 하지만 반대로 운이 안좋으면 좋지 못한 accuracy를 얻을 것이기에 이들의 평균을 통해서 최종 learning curve를 그려주는 것이다.

Limitations of Using a Single Training / Test Partition

전체 data를 하나의 partition을 통해서 training set과 test set으로 나누게 되면 문제가 생길 수 있다. 우리는 충분히 큰 training set과 test set을 만들기에 충분한 data를 가지고 있지 않을 수 있다. Data set이 존재하지만 그 양이 많지 않을 수 있다는 것이다. 그래서 이를 하나의 partition으로 나눴을 때 만약 test set이 너무 적으면 충분한 evaluation을 할 수가 없다. 일반적으로 training set과 test set을 어느정도의 비율로 나누는 것이 좋은지 생각해봤을 때 이는 매우 tricky한 질문일 수 있다. 충분히 큰 test set의 경우 우리에게 더욱 믿을만한 accuracy의 추정치를 줄 수가 있다. 하지만 반대로 충분히 큰 training set의 경우에는 우리가 실제로 학습 과정을 위해 얼마나 많은 data를 가지고 있는지를 더 잘 나타낼 것이다. 그렇기 때문에 사실상 우리는 training set과 test set을 나누다고 하더라도 양쪽 모두에서 충분한 양을 가지고 싶어하는 것이다. 그리고 하나의 training set이 특정 training sample에 대한 accuracy가 얼마나 민감한지를 말해주지는 않는다.

Using Multiple Training/Test Partitions

그래서 우리는 하나의 partition이 아닌 여러 partition을 사용하고자 하는 것이고 일반적으로는 2가지 접근 방법이 존재한다. 하나는 random resampling이고 다른 하나는 cross validation이다.

1. Random Resampling

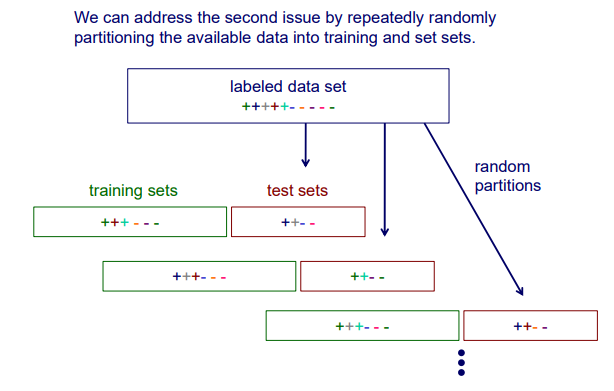Random resampling은 위와 같이 전체 data set이 있을 때, 무작위로 여러번 training set과 test set으로 나뉘게 된다. 무작위로 partition이 생기고 이것이 여러번 발생하게 된다. 그리고는 각 경우마다 training set으로 model을 학습시키고는 test set으로 accuracy를 측정하게 된다. 동일한 model을 여러 경우에 대해서 학습을 시키는 것이기 때문에 마지막에는 이들의 average를 구해줘야 한다.

2. Stratified Resampling

우리가 무작위로 training set과 test set으로 나눌 때 선택된 각 set에서 class의 비율이 유지되도록 보장할 수 있다. 이것이 의미하는 것은 무엇일까? 위와 같이 labeled data set에 12개의 plus와 8개의 minus가 존재한다고 해보자. 그리고 무작위로 sampling을 통해서 training set과 test set을 나눌 것이다. 여기서 우리가 원하는 것은 기존의 12:8이라는 비율 자체를 training set과 test set에도 그대로 유지하고 싶은 것이다. 우연히 모든 plus가 training set에 존재하고 모든 minus가 test set에 존재할 수도 있는 것이다. 그렇기 때문에 우리는 처음 비율을 그대로 유지하기를 원하는 것이고, 이 방식을 stratified resampling이라고 하는 것이다. Class label distribution의 비율을 유지하고 여기서 추가로 training set으로부터 validation set을 다시 sampling 할 수 있다. 이 부분에서는 신경을 많이 써야한다.

다시 전체 data set으로부터 training set과 test set으로 나누게 되면 실제로 test set은 모른 상태로 오로지 training set만을 이용해서 학습을 진행할 것이다. 하지만 앞서 비율을 유지하고자 하는 것이 목적이었기 때문에 대안으로 접근이 가능한 training set을 다시 training set과 validation set으로 나눌 것이다. Validation set도 마찬가지로 model이 잘 동작하는지 확인하기 위해서 사용해야 하기 때문에 접근이 가능하다. 하지만 이는 곧 기존의 training set을 더 작은 크기의 training set으로 만드는 행위이다. 그리고 이제는 test set과 validation set을 혼용해서 알고 있으면 안된다.

다시 stratified resampling을 살펴보면 label distribution의 비율을 유지하고 싶은 것이고 이는 stratified sampling을 통해 충분히 가능하다. 먼저 class별로 instance를 계층화한 다음 각 class의 instance를 비례적으로 무작위로 선택하면 된다. 처음에는 plus인 sample들과 minus인 sample들을 서로 나눈 뒤에 각각으로부터 일정한 비율로 sample들을 선택해서 training set과 test set을 구성하는 것이다.

Cross Validation(n-folds)

Training set과 test set의 partition이 주어지지 않은 상황에서 사람들이 가장 많이 사용하는 방법 중 하나가 바로 cross validation일 것이다. 주어진 data set이 training set과 test set으로 명확하게 구분이 되어 있지 않다면, random resampling을 할 수도 있지만 좀 더 보편적으로는 cross validation을 할 것이다.
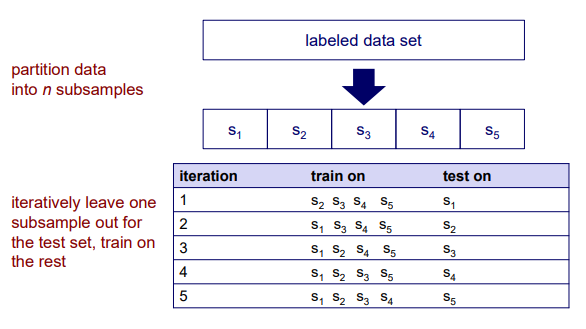Cross validation은 우선 data set이 주어졌을 때 $n$개의 subsample들의 set으로 우선 $k$개의 partition을 만들고 시작한다. 위의 경우에는 5개의 subset으로 나눈 것이고 이는 다른 말로 5-fold라고 이야기할 수 있다. 그리고 이제부터는 이 5개의 set 중에서 4개의 subset은 training에 사용하고 나머지 1개의 subset은 test에 사용할 것이다. 그리고 우리는 이 과정을 총 5개의 subset으로 나눴기 때문에 5번 진행할 것이다. 즉, 하나가 test에 사용되면 나머지는 training에 사용되는 식으로 모든 subset을 한번씩 test에 사용하고자 하는 것이다.

만약 1개의 sample만을 test에 사용하고 나머지 전부를 training에 사용하면 어떻게 될까? 이 또한 가능한 경우이며, 우리는 이를 Leave-one-out cross validation 혹은 Jackknife라고 부른다.

Example

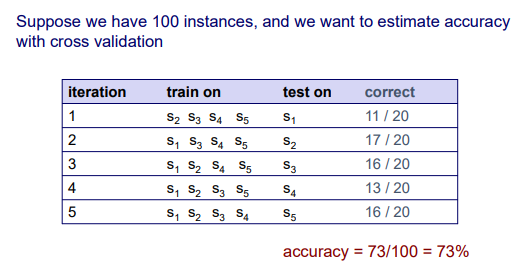우리가 총 100개의 instance들을 가지고 있다고 가정했을 때 우리는 5-fold cross validation을 이용해서 accuracy를 추정하고자 한다. 즉, 총 100개의 instance들을 20 / 20 / 20 / 20 / 20으로 나누겠다는 것이다. 총 5개의 subset으로 나눴기 때문에 총 5번의 반복을 통해서 그 결과를 구하게 될 것이다. 하나의 subset을 test에 사용하기 때문에 나머지 4개를 학습에 사용할 것이고, 각 test set에 대한 accuracy를 우리는 매 반복마다 구할 수 있을 것이다. 각 iteration마다 하나의 test set에 대한 accuracy를 구했다고 했을 때 이후에 최종 accuracy를 구할 필요가 있다. 그리고 이는 각각의 결과를 모두 더하게 되면 총 100개의 instance들에 대한 최종 accuracy를 구할 수 있다. 사실 더하는 것은 하나의 방법일 뿐이고 average를 구할 수도 있는 것이다.

Summary

1. 일반적으로는 10개의 subset을 사용하는 10-fold cross validation이 주로 사용되지만, 학습에 시간이 오래 걸리는 경우에는 종종 적은 개수로 subset을 나눠서 사용하기도 한다. 10-fold cross validation이라고 한다면 10번의 iteration 동안 총 10번의 evaluation 과정이 동반될 것이다. 하지만 만약 training과 test를 할 때 시간이 오래 걸리는 상황에서는 10-fold가 아니어도 이보다 더 작은 숫자를 사용하기도 한다는 것이다.

2. Leave-one-out cross validation에서는 $n$이 instance의 총 개수가 된다. 상대적으로 instance의 개수가 적은 data set에 대해서 이렇게 하기도 한다.

3. Stratified cross validation에서는 data를 split할 때 stratified sampling을 사용한다. 그렇기 때문에 각각의 fold마다 class label distribution의 raito를 유지할 수 있다.

4. Cross validation은 test를 위해 사용 가능한 training data를 효율적으로 사용한다.

5. 우리가 cross validation이나 random resampling 등에서 여러개의 training set들을 사용할 때마다 개별 학습 된 model을 평가하기 보다는 전체적으로 학습 방법을 평가하고자 한다. 조금 전의 예시를 다시 살펴보면 어떠한 test set에서는 low accuracy를 보이는 반면에 어떠한 test set에서는 high accuracy를 보이고 있다. 사실 특정 test set에 대해서 high accuracy를 보이고 있다는 것은 다른 test set에 대해서는 low accuracy를 보이는 것과 같은 이야기이다. 여기서 우리가 이야기하고자 하는 것은 하나의 경우에서 좋은 결과를 얻었다고 할지라도 우리는 전체적인 data set을 전부 보기를 원한다는 것이다. 그래서 우리는 model을 디자인 할 때 우리가 디자인한 이 model에 대해서 전반적인 성능을 평가하고 싶은 것이지, 각각의 subset에 대해서 성능을 평가하고 싶지 않겠다는 것이다.