Decision tree뿐만 아니라 여러 다른 data mining algorithm들에는 저마다의 issue들이 존재한다. 이번에는 decision tree를 중심으로 data mining algorithm을 적용할 때 발생하는 issue들에 대해서 알아보려고 한다.
Classification Errors
Training dataset은 learning algorithm을 이용해서 학습을 진행하고, 이로 인하여 학습된 model이 생기게 된다. 여기서 learning algorithm이라고 한다면 예를 들어 decision tree를 이야기할 수 있다. 그리고는 test dataset을 model에 적용시키게 되면 class label을 예측할 수 있게 된다. 이때, 다음과 같이 3가지 error를 맞이하게 된다.
1. Training Errors : Errors committed on the training set
Training error는 training set에서 발생한 error이다. 만약 매우 복잡한 문제를 풀어야 하거나 training dataset에 noise가 많이 존재하게 되면, algorithm이 최대한 노력을 한다고 하더라도 완벽하게 만족시킬 순 없을 것이다. Model을 학습시킬 때의 목적은 training error를 최소화하는 것이다.
2. Test Errors : Errors committed on the test set
Test error는 test set에서 발생하는 error이다. 학습된 model에 test set을 적용시키고자 할 때 발생하는 error이다. 실제로 test error는 우리가 어떻게 통제할 수는 없을 것이다.
3. Generalization Errors : Expected error of a model over random selection of records from same distribution
이상적인 경우는 training error가 model에 의해서 최소화 되는 것이고, 이 error가 test error와 generalization error과 같아야 한다. 그렇다면 이러한 상황이 실제로 발생할까? 대부분의 경우 우리는 이 generalization error를 평가하지도 못할 것이다. Training error와 test error는 대부분의 시간을 우리가 다룰 수 있게 된다. 그리고는 이 두가지 error를 최대한 같아지게 만들도록 해야 한다.
Bias를 알아봤었는데 bias의 식을 다시 생각해보면 estimated parameter의 expectation에서 true parameter를 뺀 것이 bias의 정의였다. 이때 우리는 unbiased estimator를 만들어주기를 원하고, error의 관점에서 봤을 때 앞의 term을 test error로 볼 수 있고 뒤의 term을 training error로 볼 수 있다. 즉, test error와 training error를 같아지게 하는 것이 unbiased한 결과를 만들어낸다고 볼 수 있고 이것이 우리가 원하는 결과가 된다. Generalization error를 일단은 제외하고 생각했을 때 test error와 training error를 동일하게 만들어주고자 한다. 만약 이들이 같지 않다면 우리의 model에는 어떠한 문제라도 발생하게 될 것이다.
Example Dataset
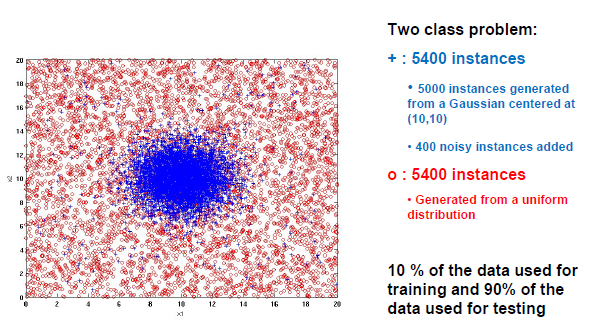위와 같이 2차원의 space에서 2종류의 instance가 있다고 했을 때 아마 중앙에 원을 그리면 된다고 생각할 것이다. 하지만 원을 그린다고 하더라도 대부분은 구분할 수 있겠지만 어느정도 error는 존재할 것이다.
위에서 blue cross instance들을 보면 5400개 중에서 5000개는 (10,10)을 Gaussian center로 하여금 2차원에서 Gaussian distributuion을 만족하면서 존재하는 data들이다. 그리고 400개의 noisy instance들을 추가한 것이다. 중앙을 제외하고도 여기저기에 noise들이 존재하는 것을 볼 수 있다. 이번에는 red circle instance들을 보면 5400개 모두가 uniform distribution으로부터 존재하는 data들이다. 그림과 같이 모든 영역에 걸쳐서 분포하고 있는 것을 볼 수 있다.
이 상황에서 10%의 data는 training에 사용하고 90%의 data는 test에 사용한다고 해보자. 그리고 여기서 decision tree를 사용하게 되면 어떠한 일이 발생할까?
Increasing Number of Nodes in Decision Trees
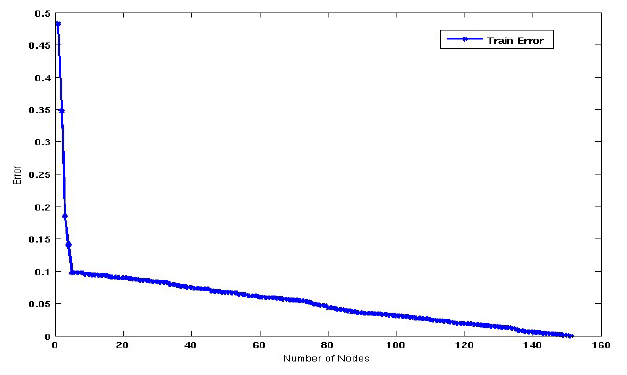그러면 위와 같은 graph를 마주하게 될 것이다. Node의 개수가 많아지면 많아질수록 training error가 줄어드는 것을 확인할 수 있다. 초반에는 급격하게 줄어들어가 어느 지점부터는 천천히 줄어드는 경향을 보이고 있다. 우리는 여기서 기울기를 유심히 볼 필요가 있다. 초반에 급격하게 줄어드는 구간은 학습이 빠르게 진행되는 구간이다. 반면, 어느 지점부터 천천히 줄어드는 구간은 반대로 학습이 천천히 진행되는 구간이다.
우리는 아마도 Gaussian center 부근에 있는 모든 instance들에 무언가를 했다는 것을 쉽게 알 수 있다. 이후에는 주변의 noise instance들과 무언가를 했다는 것을 알 수가 있다. 이는 다시 data distribution에 대해서 생각해 볼 필요가 있다. 5400개의 instance들 중에서 400개의 instance는 noise였다. 이는 약 10% 정도의 blue cross instance들은 쉽게 구분하기 어렵다는 이야기이다. 아무래도 Gaussian center 부근의 data 외에도 주변에 널리 퍼져있는 noise들 때문에 classification 결과가 완벽하도록 기대하기에는 어려움이 존재할 것이다. 그렇기 때문에 초반에 적은 node 개수만으로 90% accuracy를 보이게 되는 것이다. 이후에는 noise 때문에 node의 개수가 많아지면 많아질수록 성능이 조금씩 좋아지는 것을 확인할 수 있다.
그렇다면 여기서 의문점은 noise들 때문에 완벽한 성능을 위해서 node의 개수를 정말로 많이 늘려야 한다는 것일까? 위의 graph만 보게 되면 약 150개의 node가 존재할 때 100%의 성능을 보이게 된다. 정말로 이렇게까지 하는 것이 좋은 classifier라고 할 수 있을까? 이러한 종류의 dataset 때문에 여러가지 issue가 발생할 수 있다. 이는 decision tree만의 문제가 아닌 여러 다른 algorithm들에서도 확인할 수 있는 문제들이다.
Decision Tree with 4 Nodes
그렇다면 이제부터 어떠한 일이 발생하는지를 확인해보도록 하자. 가장 먼저 급격하게 training error가 줄어들다가 변화하는 4개의 node인 지점을 확인해보도록 하자.
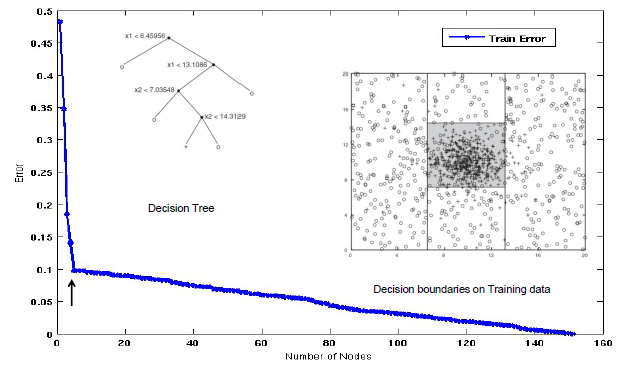Decision tree에 따라 해당 feature로부터 decision boundary를 그려가면서 instance들을 나눠주게 된다. 그렇게 되면 총 4번의 branching out 과정을 통해서 우측과 같이 영역을 구분하게 되고 90% accuracy를 보이게 될 것이다.
Decision Tree with 50 Nodes
만약 여기서 더 진행하게 된다면 어떻게 될까? 4개의 node 만으로는 위의 결과에서 모든 instance들을 완벽하게 나눴다고 이야기하기는 어려울 것이다. 그래서 이제는 model이 정확하게 분류하지 못한 instance들에 대해서 다뤄야 할 필요가 생기게 된다.
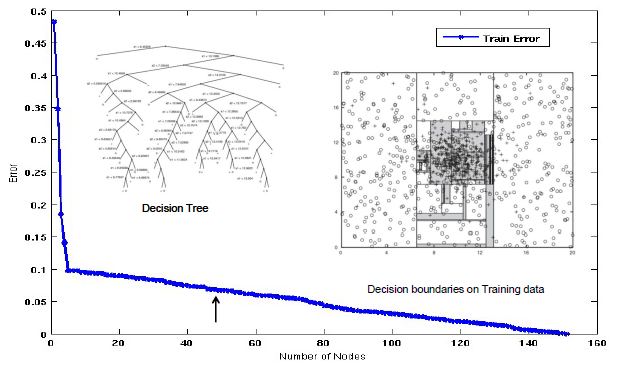그래서 50번의 branching out을 더해주게 되면 간단한 2차원의 space에서 엄청나게 복잡한 decision tree가 만들어지게 될 것이다. 성능이 기존 4개의 node 때보다 증가했지만, model이 복잡해지고 decision boundary가 굉장히 많아진 것을 볼 수 있다.
Which Tree is Better?
그래서 우리는 이 2가지 경우를 비교해볼 필요가 있다. 4개의 node를 가지는 tree와 50개의 node를 가지는 tree 중에서 어떠한 tree가 더 나을까?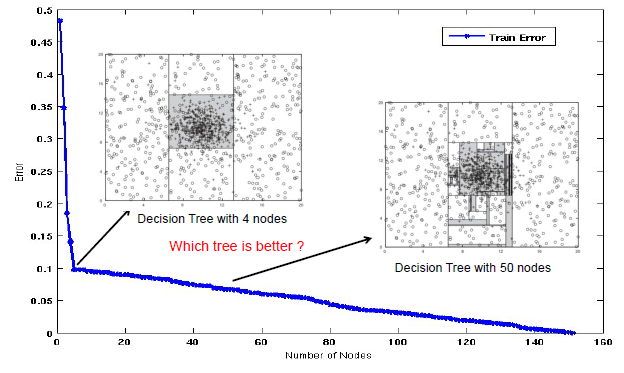
Training error의 관점에서 전자는 0.1이고 후자는 약 0.06이기 때문에 50개의 node를 가지는 tree가 더 좋다고 이야기할 수도 있다. 그렇다면 이정도 차이의 training error를 줄이기 위해서 50개까지의 node를 사용하는 것이 과연 옳은 선택일까? 아무래도 이정도의 차이라면 그냥 4개의 node를 가지는 tree를 사용하는 것이 더 좋을지도 모른다. 이는 Occam's Razor에 기반하여 더 간단한 model을 선택한 것이다. 2개의 model이 차이가 크지 않고 비슷한 성능을 보이고 있다면, 아무래도 더 간단한 model이 더 낫다는 이야기다.
Model Underfitting and Overfitting
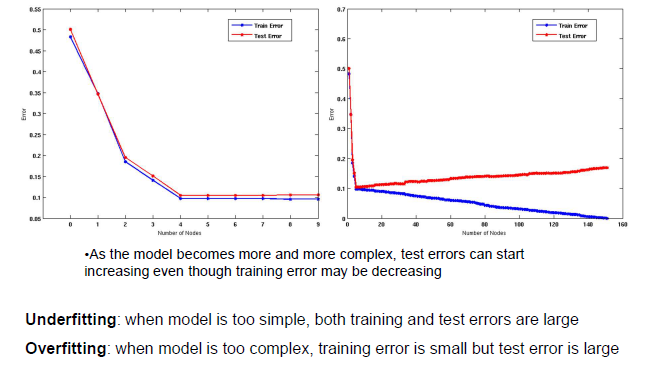Tree가 만들어지게 되면 node의 개수가 늘어남에 따라 algorithm의 training error를 줄이려고 할 것이다. 그리고 각 node의 개수에 따른 학습된 model로 test set에 적용시키게 되면 training error와 test error가 node가 적은 부분에서는 매우 동일한 것을 확인할 수 있다. 좌측의 graph에서 보다시피 대략 9개의 node까지는 2가지 error가 비슷한 경향을 보이는 것을 알 수 있다.
이번에는 node의 개수가 그 이상 증가하면 어떻게 되는지 생각해보고자 한다. 우측의 graph에서 보다시피 우리가 training error를 0으로 만들기 위해서 무수히 많은 node를 사용하게 되면 training error가 완전히 사라져 기분이 좋을 수도 있다. 그러나 이렇게 학습된 model에 test set이 적용되게 되면 node의 개수가 증가할수록 test error가 줄어드는 것이 아닌 늘어나는 것을 볼 수 있다.
그래서 training set에 대해서 accuracy가 매우 높아지게 된다면, 이는 오히려 test set에서는 accuracy가 떨어지게 만들 수가 있다. 우리는 이러한 상황을 overfitting이라고 부른다. Overfitting은 model이 매우 복잡해지게 된다면 training error가 줄어들게 되지만 역으로 test error는 증가하는 것을 이야기한다. 이러한 상황은 아무래도 피해야 하는 상황일 것이다.
Underfitting은 overfitting과는 다르게 model이 간단한 경우에 발생한다. Model이 너무 간단해지게 된다면 training error와 test error 둘 다 높게 측정될 것이다. 아무래도 underfitting이 overfitting보다 다루기는 쉬울 것이다. Overfittint이 발생하면 해결하는데 다소 어려움이 존재한다.
Model Overfitting - Impact of Training Data Size
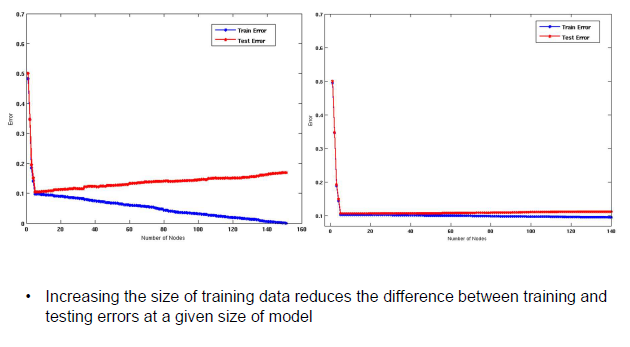Overfitting은 최대한 피해야 하며, training data의 크기를 증가시키게 되면 training error와 test error 사이의 차이를 줄일 수가 있다. Overfitting을 피하는 방법 중 하나로 더 많은 data를 사용하자는 것이다. 앞서 우리는 10%의 data만을 training data로 사용한다고 했었다. 여기서 이 비율을 20%, 30% 정도로만 올린다고 하더라도 충분히 error간 차이를 줄일 수 있게 될 것이다.
Decision tree가 더 복잡해진다는 것은 branching out을 더 많이 진행한다는 것이고 이는 더 많은 node를 필요하게 된다. 이는 deep learning의 관점에서 더 많은 parameter를 동반해야한다는 이야기이기도 하다. 그렇게 되면 더 많은 parameter를 추정해야 하는데, 이는 더 많은 data가 필요하다는 것이 된다. 즉, model이 복잡해지게 되면 data도 그만큼 많이 필요하다는 것이다.
Reasons for Model Overfitting
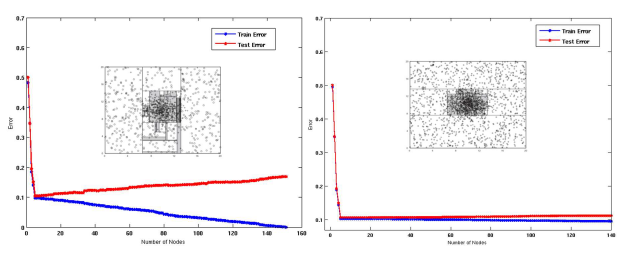좌측은 기존과 같이 10%의 data를 training set으로 사용한 결과이다. 반면, 우측은 20%의 data로 그 비중을 늘리 결과이다. Data의 양을 늘려주기만 했을 뿐인데 decision boundary를 봐도 20%가 더 안정적이게 된 것을 확인할 수 있다.
Decision tree에서 branch를 만드는 것은 impurity measure를 기반으로 진행한다. Impurity measure는 cluster 중앙에 decision boundary를 남기도록 만들 수가 있다. 그래서 바깥의 sample들에 초점을 맞추기 보다는 decision boundary를 중앙쪽으로 계속해서 그려나가게 되는 것이다.
그렇다면 overfittin이 왜 발생하는 것일까?
1. Not enough training data
일반적으로는 training data가 충분하지 못해서 그렇다. 추정해야하는 미지수들이 많지만, 이를 해결할 식의 개수는 부족한 것이다. Sample이 충분하지 못하면 overfitting이 발생하는 것이다.
2. High model complexity
이는 model이 복잡하다는 것을 의미하기도 한다. 다소 복잡한 model을 충분히 학습하는데 필요한 data가 적을 수 있다. 여기서 model complexity는 multiple comparison procedure라는 term으로 설명될 수 있다.
Effect of Multiple Comparison Procedure
Multiple comparison procedure란 무엇일까? 간단하게 이야기하면 어떠한 것을 비교하는데 이를 여러번 하겠다는 것이다. Decision tree만 하더라도 여러번의 비교를 통해서 label을 결정하게 되는데, 그렇다면 이는 왜 중요한 것일까?
먼저 이는 statistics와 관련된 term이다. 직관적으로 이해를 돕기 위해서 대략 50명의 분석가가 있다고 해보자. 그리고 각 분석가는 10개의 random guess를 만들게 된다. 우리는 올바른 예측을 가장 많이 한 분석가를 골라야 한다. 아마 10개의 예측이 모두 다 맞는 사람이 존재할지도 모른다. 적어도 우연히 8개의 올바른 예측을 한 분석가가 존재할 수도 있다. 여기서 만약 많은 대안을 사용할 수 있는 경우, model에 무관한 component들을 실수로 추가함으로써 overfitting이 발생할 수 있다.
비록 branching component나 올바른 예측을 하는 classifier가 존재한다고 하더라도, 이는 무작위로 일어났을 가능성도 존재한다. 하지만 우리가 tree를 만들 때 branch들이 도움이 될 것이라는 가정을 했기에 무관한 component들은 실제로 문제를 야기할 수 있다. 왜냐하면 아무래도 impurity를 줄여가면서 더 많은 branch를 얻었기 때문이고, 이로 인하여 올바른 예측을 하고 있다고 생각했기 때문이다. 이러한 가정들 속에서 전혀 상관없는 component를 model에 추가하는 것은 결과적으로 overfitting을 발생하는 원인이 된다.
그래서 branch를 만드는 방법이 다수 존재하고 많은 feature들을 고려하면서 우리는 branch를 만드는 것이 성능을 향상시킬 것이라고 기대하게 된다. 하지만 문제는 이러한 상황이 무작위로 발생할 수 있다는 것이다. 그리고 우리는 이를 multiple comparison procedure라고 하는 것이다. 50개의 branch를 늘려가는 방법들, 혹은 50개의 model 개선 방법들 중에서 몇가지는 model을 향상시키는 것이 우연히 발생한다는 것이다. 그리고 이러한 상황이 decision tree에서도 발생할 수 있다는 것이다.
앞서 적어도 8개의 올바른 예측을 할 확률이라는 것을 계산해보면 다음과 같다.
50개의 분석가들이 10개의 random guess를 하고 이 중에서 적어도 8개의 예측이 맞을 확률이 약 94%로 높은 편에 속하게 된다.
Notes on Overfitting
- Overfitting results in decision trees that are more complex than necessary
그렇기 때문에 우리는 tree를 복잡하게 늘리고 싶지 않은 것이다. 혹은 우리의 model을 복잡하게 구성하고 싶지 않은 것이다. 왜냐하면 오로지 training set에서만 우연한 결과로 성능이 향상된 경우도 존재하기 때문이다. 그래서 overfitting은 decision tree를 필요 이상으로 복잡하게 만들 수가 있다. 간단한 문제에는 간단한 decision tree를 사용하면 되고 복잡한 문제에는 복잡한 decision tree를 사용하면 된다. 간단한 문제에 복잡한 model은 overfitting의 원인이 되기 때문에 원하지 않는다.
- Training error does not provide a good estimate of how well the tree will perform on previously unseen records
Training error는 이전에 보이지 않았던 record에서 tree가 얼마나 잘 수행될지에 대한 좋은 추정치를 제공하지 않는다. 여기서는 test set에 해당할 것이다. 그렇기 때문에 training error로부터 test set에 대한 좋은 추정을 할 수 없어서 validation set이 필요한 것이다.
- Need ways for estimating generalization errors
이제는 training set, validation set, test set을 확실히 구분해야 하며, test set에 대한 generalization error를 추정할 방법들이 필요하게 된다. Test set뿐만이 아닌 어떠한 새로운 data에 대한 일반적인 방법이 있어야하는 것이다.
Model Selection
그래서 우리는 model을 선택해야 한다. Decision tree를 만들 때 4개의 node를 사용해도 되고 9개의 node를 사용해도 된다. 이 외에도 무수히 많은 경우가 존재할 것이고, 이 중에서 어떠한 경우를 선택해야 하는 것일까? 이렇게 model을 만들 때 여러 경우 중에서 선택하는 상황을 model selection이라고 한다.
Model selection을 하는 목적은 overfitting을 막고자 model이 지나치게 복잡하지 않도록 하기 위해서이다. 4개, 9개, 50개 등 여러 경우에서 어떻게 고르는지에 대해서는 generalization error를 추정할 필요가 있는 것이고, 이는 validation set을 이용하면 된다. 아니면 training 과정에서 model complexity를 통합하면 된다. 즉, 우리는 초기 목적인 training error를 줄이는 것과 동시에 model complexity도 동시에 줄이는 방법을 생각하면 된다.
1. Using Validation Set
Training data를 2개로 나눠서 하나는 그대로 training set으로 두고 다른 하나는 validation set으로 만들면 된다. Training set은 model을 만들 때 사용이 된다. Validation set은 generalization error를 추정할 때 사용될 것이다. 이 상황에서 generalization error는 test error로 봐도 무방하다. 우리는 validation error와 test error를 동일하다고 가정한다는 것이다. 하지만 여전히 중요한 점은 validation set과 test set은 다르다는 사실이다.
2. Incorporating Model Complexity
두번째 option은 model complexity를 training 과정에 함께하도록 만드는 것이다. 그 이유로는 Occam's Razor를 이야기할 수 있다. 현실에서도 너무 복잡하게 생각하는 것은 좋지 않다.
2가지 model로부터 비슷한 generalization error가 주어졌을 때, 우리는 더 간단한 model을 선호할 것이다. 왜냐하면 복잡한 model의 경우 우연한 결과를 가져왔을 가능성이 더 크기 때문이다. 이는 앞서 살펴본 multiple comparison의 이유이기도 하다. 그렇기 때문에 model complexity를 model을 평가하는 과정에 함께 포함해야 하는 것이다. 그리고 다음과 같이 종합적으로 error를 최소화해야 한다.
Model Selection for Decision Trees
그렇다면 이는 decision tree에서는 어떻게 할 수 있을까? Pre-pruning과 post-pruning을 통해서 할 수 있으며, 여기서 pruning은 몇몇 branch를 잘라내는 것을 말한다.
1. Pre-Pruning(Early Stopping Rule)
Pre-pruning은 tree를 다 만들기 전에 branch를 잘라내는 것을 말한다. 그래서 이를 early stopping이라고도 이야기하는 것이다. 일반적으로 stopping condition은 특정 node에서 모든 instance들이 동일한 class에 속하거나 모든 attribute value들이 동일한 경우에 해당하게 된다. 이외에도 더 제한적인 stopping condtion들도 존재한다.
- Instance들의 숫자가 우리가 정한 threshold보다 더 적은 경우에 멈출 수가 있다. 만약 특정 node에서 sample의 개수가 10개가 안된다면 이 상태로 멈춰도 된다는 것이다.
- 아니면 instance들의 class distribution이 가능한 feature들에 대해 independent한 경우에도 멈출 수가 있다. 일반적으로 attribute에 따라서 branch를 나누곤 한다. 하지만 class distribution이 특정 feature와 상관관계가 존재할 수도 있는 것이다. 이때 크게 상관이 없으면 branch를 이어나가는 것이다.
- 현재의 node를 확장시키는 것이 Gini나 information gain와 같이 impurity measure가 더 개선이 되지 않는다면 멈춰도 된다. Gain이 특정 threshold보다 더 적으면 굳이 더 branch를 늘려나가지 않는 것이다.
- 추정된 generalization error가 특정 threshold보다 아래로 떨어지게 된다면 멈추는 방법도 있다. 이는 validation set을 이용할 때일 것이다.
만약 길을 걷다가 10원을 발견하면 주울 것인가? 물론 대부분 주울 것이지만 이를 줍기 위해서 에너지를 사용할 것인지를 생각해봐야 한다. 10원을 줍는 것이 정말 가치가 있는지 계속해서 물어보고 판단해야 한다.
2. Post-Pruning
Post-pruning은 먼저 tree를 다 만들어 놓은 다음에 branch를 잘라내는 방식이다. Post-pruning에는 subtree replacement라는 것이 존재한다. Subtree replacement는 decision tree의 node들을 bottom-up 방식으로 다듬는 것이다. 물론 여기에도 기준이 존재한다. 만약 validation set을 이용하여 generalization error가 trimming 이후에 개선이 된다면 sub tree를 leaf node로 대채할 수가 있다. 우리가 하나의 branch를 자른 후에 validation accuracy가 증가한다면 잘린 node를 제외시켜서 sub-tree를 하나의 leaf node로 대채할 수 있다는 것이다. Leaf node의 class label은 sub-tree instance들의 다수 class에서 결정이 된다.
