Data = Data Objects + Attributes
Data는 data object들과 이들의 attribute들을 모아놓은 것이다. 여기서 data object는 data sample 혹은 example이라고 부르며, data mining이나 data science에서 주로 말하는 data는 이러한 data sample들과 이들이 가지고 있는 attribute들을 모아놓은 것을 말한다. 그리고 여기서 attribute를 feature라고도 부른다. 예를 들어 사람의 얼굴을 하나의 data sample이라고 해보자. 이 사람의 얼굴을 표현하기 위해서는 이 data sample을 보고 생각할 수 있는 attribute들이 존재해야 한다. 큰 귀, 두꺼운 눈썹, 오똑한 코, 네모난 입, 파마 머리 등이 attribute에 해당하며, 이러한 attribute를 사용해서 해당 data object를 설명할 수 있다. 이렇게 여러개의 attribute를 통해서 하나의 data sample을 설명할 수 있다면, 여러개의 data sample들을 만들 수가 있기에 이러한 것들을 모아놓은 것을 우리는 data라고 하는 것이다. 보통 이러한 data는 다음과 같이 table 형식으로 정리할 수 있다.
위의 예시는 총 10개의 sample들과 각각을 설명하는 attribute가 4개 존재하는 data matrix이다. 만약 id를 포함시키고 싶으면 총 5개의 attribute가 존재하는 셈이다. 각 attribute는 결국 특정 질문에 대한 답변으로 구성되어진다.
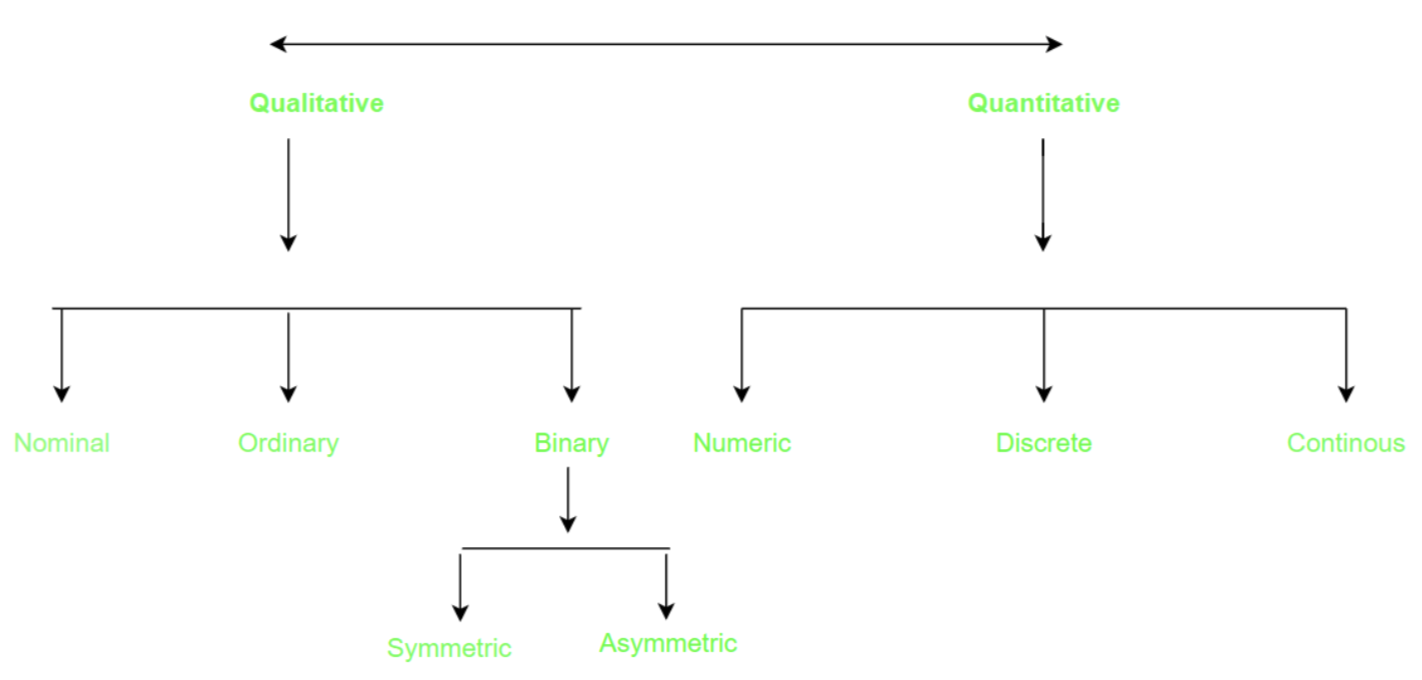Attribute를 정의해보면 결국 object에 대한 property와 characteristic을 의미한다. 예를 들어 다시 사람을 설명하고자 한다면 눈의 크기, 색 등 사람을 설명할 수 있는 모든 것들이 attribute가 될 것이다. 통계학에서는 attribute를 variable이라고도 부르며, machine learning에서는 feature라고도 부른다. 이외에도 다른 분야에서는 attribute를 field, characteristic 등으로 부르기도 한다.
하나의 attribute로 object를 설명할 수도 있지만, 보통은 여러개의 attribute들을 모아서 하나의 object를 설명하곤 한다. Object는 또한 여러 분야에서 sample, record, (data) point, case, entity, instance 등으로 부를 수 있다. Object를 data point라고도 부르는데에는 관점을 살짝 달리하면 이해할 수 있다. 위에서 data에 대해서 table로 표현을 했는데, 이는 결국 2D matrix로 바꿔서 생각할 수 있기 때문이다.
Attribute Values
Attribute value는 attribute에 할당된 number나 symbol을 말한다. 만약 어떠한 질문에 대해서 숫자로 대답할 수 있으면 이 숫자가 바로 attribute value가 될 것이고, 이 질문이 숫자가 아닌 어떠한 명칭이 있다면 이 명칭이 attribute value가 될 것이다. 간단하게 yes나 no로 대답할 수 있는 질문에 대해서는 yes와 no가 symbol로서 attribute value가 될 것이다. 결국 attribute value의 형식은 질문하는 형식에 따라 정해지게 되는 것이다.
- Distinction between attributes and attribute values
사실 이보다 더 중요한 것은 attribute와 attribute value를 구분하는 것이다. Attribute는 일종의 질문에 해당하는 것이고, attribute value는 대답에 해당하는 것이다. 동일한 attribute일지라도 서로 다른 attribute value에 mapping될 수 있는 것이다. 예를 들어 누군가의 키를 물어보았을 때 meter로 답하는 사람이 있는 반면 feet로 답하는 사람이 있을 수도 있다. 키를 물어보았는데도 다른 대답을 할 수 있는 것이다.
- Different attributes can be mapped to the same set of values
만약 누군가의 ID와 나이에 대한 attribute value를 얻고자 할 때, 둘 다 정수의 형태로 대답이 가능하지만 의미상 다른 것을 가리키게 된다. 내 ID가 40이고 나이 또한 40이라고 했을 때 같은 값처럼 보이지만 실제로 다른 것을 가리키고 있는 것이다. 즉, attribute value의 property가 다를 수 있다는 것이다. 확실히 ID 값의 범위 제한은 없지만, 나이는 최소한 음수가 될 수는 없을 것이다.
- The way you measure an attribute may not match the attribute properties
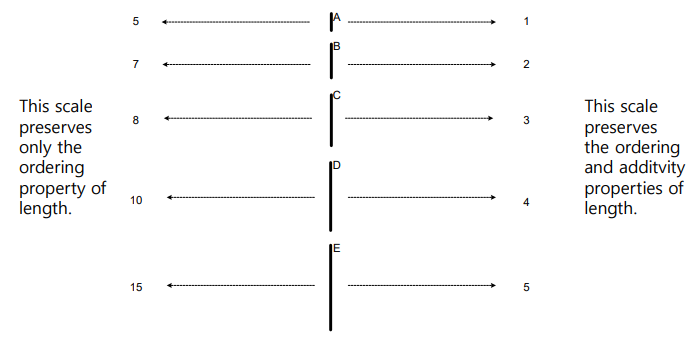위에는 서로 다른 5개의 object A, B, C, D, E가 있다. 그리고 각각의 길이를 잰다고 했을 때, 좌측과 같이 5, 7, 8, 10, 15라고 설명할 수 있다. 그리고 이들에게 순위를 부여한 것이 오른쪽의 결과이다. 여기서 우리는 각각의 길이를 측정하고 싶었고, attribute value로 둘 다 숫자를 사용했지만 그 의미는 다른 것을 알 수 있다. 좌측과 우측의 결과에서 유일한 차이는 additivity이다. Additivity나 ordering은 잠시 후에 볼 개념들이기에 살짝 넘어가고, 우선 여기서 중요한 것은 동일한 object를 어떻게 측정하는지에 따라서 완전히 다른 결과를 가져올 수 있다는 것이다. 비록 같은 object를 보고 있더라도, 다른 대답을 생각해낼 수가 있다. 다른 대답은 다른 attribute value를 만들게 되고, 어떻게 이들을 평가하는지에 따라서 이들은 서로 다른 property를 가지게 될 것이다.
Types of Attributes 1
Attribute의 type은 다음과 같이 4개로 나눌 수가 있다.
1. Nominal
Nominal은 이름과 같은 것으로, ID number, 눈의 색, zip code 등과 같은 것으로 이들은 어떠한 순서도 가지고 있지 않다. 이들은 이들 자체로 중요한 의미를 가지게 된다. 만약 attribute가 nominal attribute에 해당한다면, 누군가가 더 큰 숫자를 가지고 있다고 하더라도 실질적으로 순서나 크기와 같은 의미는 존재하지 않는 것이다. 이는 그냥 그자체로 의미가 있게 된다.
2. Ordinal
Ordinal은 이제부터는 어떠한 비교가 생길 것을 의미한다. 예를 들어, 순위, 성적, 키 등과 같이 해당 결과를 다른 결과와 비교하여 순서를 매길 수 있으면 이는 ordinal attribute가 되는 것이다. 숫자로 비교도 가능하지만, tall과 short처럼 어떠한 문자로도 비교가 가능할 수 있다. 여기서 핵심은 순서가 발생하여 비교가 가능해진다는 것이다.
3. Interval
Interval의 예시로는 달력의 날짜, 섭씨 온도, 화씨 온도 등이 해당한다. 이들은 숫자로 표현되면서 이들은 상대성이 존재하게 된다. 현재 기온이 섭씨 16도이고 아침의 기온이 섭씨 8도라고 했을 때 현재 기온이 아침의 기온보다 2배 높은 것을 알 수 있다. 하지만 이를 interval attribute에서는 2배 높다고 할 수가 없다. 대신에 8도의 간격을 두고 차이가 존재한다고는 할 수 있다. 섭씨 온도를 통해서 2배 만큼 따듯한 것이 아니기 때문이다. 그리고 이들을 그대로 화씨 온도로도 바꿀 수 있을 것이고, 이들 사이에도 간격이 존재할 것이다. Interval attribute는 균일한 간격을 두고 측정을 해서 수치 간에 차이가 의미를 가지게 되는 것이다. 그리고 여기에는 절대적인 원점인 zero-point가 없기 때문에 덧셈과 뺄셈만이 그 의미를 가지게 된다.
4. Ratio
Ratio는 interval과는 다르게 절대적인 기준이 존재하게 된다. 대표적으로 켈빈 온도가 여기에 해당하며, 길이, 무게, 개수 등 우리가 다루는 대부분이 ratio attribute에 해당한다. 여기서는 20K가 10K보다 2배 높다고 이야기할 수 있다. 길이를 봐도 20cm가 10cm보다 2배 길다고 이야기할 수 있는 것이다. 만약 내 친구가 15초 달리는 동안 내가 1분을 달렸다면, 내 친구가 나보다 4배만큼 빠르다고 이야기 할 수 있다. 이 모든 것을 종합해서 ratio attribute는 scale을 보존하는 것을 알 수 있다. 그리고 interval attribute와는 다르게 zero-point가 존재하여 모든 사칙 연산이 가능하게 된다.
Types of Attributes 2
Attribute의 type은 각각 가지고 있는 property나 operation에 따라서 나뉘기도 한다. 이는 좀 더 명확하게 4개의 attribute가 각각 어떠한 성격을 지니는지 확인할 수가 있다. 다음과 같이 4개의 성질이 있다고 해보자.
- Distinctness :
- Order : <, >
- Differences are meaningful : +, -
- Ratios are meaningful : *, /
그리고 다음과 같이 4개의 attribute를 위의 성질의 유무에 따라서 나눌 수 있는 것이다.
- Nominal attribute : distinctness
- Ordinal attribute : distinctness & order
- Interval attribute : distinctness & order & meaningful differences
- Ratio attribute : all 4 properties/operations
Nominal attribute에서는 오로지 2개의 object가 같은지 다른지만을 설명할 수 있다. Ordinal attribute 또한 같은지 다른지를 설명할 수 있지만, 여기에 추가로 누가 더 큰지 등의 순서를 매길 수가 있다. Interval attribute는 distinctness와 order에다가 덧셈과 뺄셈 또한 진행할 수 있다. 마지막으로 ratio attribute는 distinctness, order, 덧셈, 뺄셈과 더불어 곱셈과 나눗셈까지 모든 사칙연산이 가능하다.
Difference between Ratio and Interval
앞서 이야기했지만 10도라는 온도가 5도의 2배라는 물리적인 의미가 있는지에 대해서 살펴보려고 한다. 그리고 이는 온도의 종류에 따라 그 대답이 달라지게 된다. 섭씨 온도와 화씨 온도에서는 이 질문에 대해서 no가 되며, 켈빈 온도에 대해서만 이 질문에 대해서 yes가 된다. 그 이유는 앞서 살펴 보았듯이 섭씨 온도와 화씨 온도는 interval attribute지만, 켈빈 온도는 ratio attribute이기 때문이다. Interval attribute에서는 scale과 ratio가 보존되지 않는다. 반면, 켈빈 온도는 절대 온도이기 때문에 zero-point가 존재하고 scale과 ratio가 보존이 된다.
그렇다면 평균 이상의 키를 측정하는 상황은 어떻게 될까? 만약 Bill의 키가 평균보다 3인치가 크고 Bob의 키는 평균보다 6인치가 크다면, Bob이 Bill보다 2배가 크다고 이야기할 수 있을까? 아마 이 질문에 대한 대답은 no일 것이다. 평균이라는 조건이 주어졌기 때문에 이렇게 결론을 낼 순 없다. 다음은 지금까지의 내용들을 요약하는 table이다.
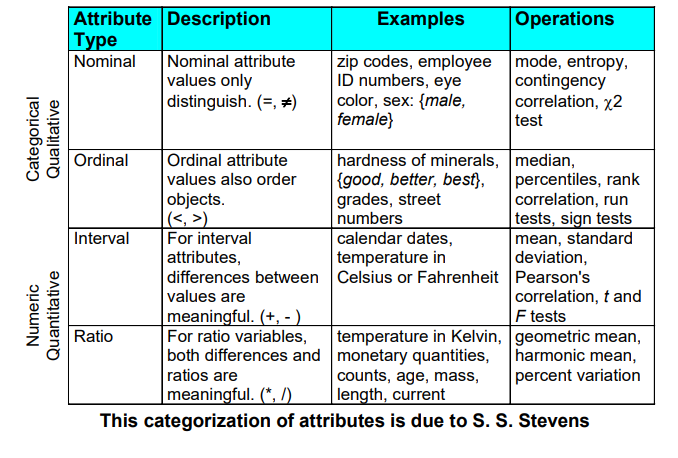여기서 nominal attribute와 ordinal attribute는 categorical qualitative에 해당하고, interval attribute와 ratio attribute는 numeric quantitative에 해당한다. 여기서 중요한 내용은 nominal operation들이 oridnal operation에 적용할 수 있고, orinal operation들은 interval operation에 적용할 수 있으며, interval operation들은 ratio operation에 적용할 수 있다. 어떠한 것이든 nominal, oridnal, interval operation에서 가능하다면, 이는 곧 ratio operation에서도 가능하다는 이야기다.
대표적인 연산 중에 mode 연산은 frequency를 나타내기에 4, 5, 5, 6, 7, 9, 9, 9에서 mode 연산을 적용하면 가장 빈도 높게 등장하는 9가 될 것이다. Median 연산은 위와 같은 경우에 대해서 정중앙에 있는 값이 6이 될 것이다. Mean은 이 값들을 다 더해서 개수로 나눠 평균을 구할 수 있을 것이다. 이렇게 하나의 dataset만 있어도 다양한 연산이 가능하다.
1. Nominal : Transformation을 보면 nominal attribute의 경우 할 수 있는 것은 오로지 단순하게 치환 혹은 순서를 섞는 것이다.
2. Ordinal : Ordinal attribute의 경우 data의 가장 앞단에 transformation을 한다고 했을 때 순서는 보존되어야만 한다. 만약 무작위로 섞는다고 했을 때, ordinal attribute에서 중요한 순서를 파괴하게 된다. 그렇게 되면 ordinal attribute로 존재하지 못하게 되기에 transformation을 한다고 했을 때, 반드시 ordinal data의 경우에 순서는 보존되어야 한다. 기존 값에 라는 함수를 취해서 새로운 값으로 만든다고 했을 때, 는 monotonic function이어야 할 것이다. 즉, transformation을 적용했을 때 순서가 변하지 않으려면 단순하게 증가하거나 감소하는 형태여야만 한다.
3. Interval : Interval attribute의 경우 모든 sample들에 대해서 동일하게 a를 곱해 scale을 바꾸고 b를 더해서 값을 변화시켜도 상관이 없다. 즉, scale과 offset을 그대로 보존하지 않고 변화시켜도 된다는 이야기다. 이러한 경우에 순서도 보존이 될 것이다. 섭씨 온도에 특정 값을 곱해서 특정 값을 더해서 화씨 온도로 변환시킬 수가 있다. 이는 interval attribute이기에 이러한 transformation이 가능한 것이다.
4. Ratio : Ratio attribute에서 가장 중요한 성질은 scale이다. 그래서 오로지 할 수 있는 것은 기존 값에 특정 값을 곱하는 것 뿐이다. 만약 키가 2배가 차이나는 두 사람이 있을 때, 두 사람의 키에 특정 값만을 곱하면 그 scale은 보존될 것이다. 하지만 여기에 특정 값을 더하게 된다면 scale이 보존되지 않고 변하게 될 것이다.
Transformation의 경우 nominal attribute에서 ratio attribute 쪽으로 향할수록 더 제한적이게 된다.
Discrete and Continuous Attributes
그렇다면 지금부터는 조금 더 구체적으로 attribute가 어떠한 값들을 취하는지에 대해서 알아보고자 한다. 지금까지는 symbol과 number에 관해서만 이야기했다. 여기서 symbol은 항상 discrete한 성질을 가지고 있지만, number는 discrete와 continuous를 둘 다 가지게 된다. 그렇다면 discrete attribute와 continuous attribute의 차이는 무엇이며 어떠한지에 대해 알아보고자 한다.
Discrete Attribute
Discrete attribute에 해당하는 것은 오로지 finite하거나 countably infinite한 값들의 집합뿐이다. 이것이 의미하는 바는 예를 들어 성적이 여기에 해당할 수 있다. 특히 A, B, C, D, F와 같이 대학교에서 부여하는 성적같은 경우가 discrete attribute인 것이다. 이러한 성적 표기는 {A, B, C, D, F}와 같이 finite set으로 묶을 수 있기 때문이다. 이외에도 우편 번호, 인구 수, 문서에 포함된 단어들과 같은 우리가 셀수 있는 모든 것들이 discrete attribute이다. Symbol뿐만 아니라 interval attribute나 ratio attribute 중에서도 종종 정수로 표현될 수 있는 것들도 또한 discrete attribute가 될 수 있다. 그리고 binary attribute는 discrete attribute 중에서도 특별한 경우에 해당된다.
Binary attribute는 0이나 1로 표현되는 attribute로 왼쪽과 오른쪽 등 2가지 경우로 표현할 수 있는 attribute가 이에 해당할 수 있다. Binary attribute는 중요한 개념으로 data mining 문제를 해결하고자 할 때 가장 간단한 경우에 해당하게 된다. 매우 복잡한 경우에 대해서도 binary하게 단순화시켜가면서 문제를 해결할 수 있는 것이다.
Continuous Attribute
Continuous attribute는 attribute value로 실수를 취하는 경우들이 해당하게 된다. 예를 들어 온도나 키, 혹은 몸무게 등과 같이 연속된 값의 범위를 가지는 것들이 continuous attribute에 해당하게 되는 것이다. 실질적으로, 실수는 finite number를 사용하여 측정되고 표현될 수 있다. 비록 continuous attribute가 있다고 하더라도, 컴퓨터에 import할 때에는 어떠한 방식으로든 discrete하게 바꾸게 되어있다. 그래도 여전히 이를 continuous attribute라고 부르는 이유는 우리가 이를 continuous함을 알고 있기 때문이다. 그리고 continuous attribute는 전형적으로 floating-point variable로서 표현이 된다.
Asymmetric Attributes
일반적으로 binary attribute는 2개의 대답 혹은 상태를 나타낼 수 있다. 이때, 2개의 attribute value 모두 동일하게 중요한 정보를 지니면 symmetric attribute라 하고, 2개의 attribute의 중요도가 동일하지 않으면 asymmetric attribute라 한다. 남자/여자와 같은 경우는 symmetric attribute에 해당하고, 네/아니오와 같은 경우는 assymetric attribute에 해당한다.
지금까지 data, object, attribute가 무엇인지에 대해 알아보았고, attribute value가 어떠한 성질들을 가질 수 있는지에 대해서도 알아보았다. 이제는 이러한 attribute들을 서로 비교해봐야 할 필요가 있다. 현실에서는 차별은 좋지 못하다고 배우게 된다. 하지만 컴퓨터를 배우는 입장에서는 어떻게 차별을 해야하는지에 대해서 알아야 한다. 사실 무언가를 학습하고 pattern을 찾는다는 것은 비교로부터 발생하게 되는 것이다. 대신에 이제부터 어떠한 차이에 대해서 이야기를 할 때 difference보다는 similarity라고 하고자 한다.
- Only presense(a non-zero attribute value) is regared as important
시작은 엄청나게 많은 양의 sample들로부터 할 것이다. 여기서 어떠한 sample들이 서로 비슷하고 어떠한 sample들이 서로 다른지에 대해서 알아보고자 하는 것이다. 이러한 비교를 하고자 할 때는 오직 존재성만이 중요하게 작용할 것이다.
예를 들어 5개의 서로 다른 attribute가 있다고 할 때 가장 먼저 해야하는 중요한 질문으로는 attribute나 attribute value가 존재하는지 혹은 비어있는지에 대한 것이다. 만약 비어있지 않다면, 해당 attribute가 어떠한 value를 가지고 있는지 물어봐야 한다. 이러한 질문들이 우리가 가장 먼저 해야하는 질문들이다. 재미있는 예시를 들어보자면, 혹시 여자친구와 크리스마스에 어떠한 것을 할 것인지를 물어보기 이전에 여자친구가 존재하는지에 대해서 물어봐야 할 것이다. 그래서 정리하면 존재성이라는 것은 가장 먼저 해당 attribute가 어떠한 value를 가지고 있는지 물어보기 이전에 정말 해당 attribute가 존재하는지를 확인해야 한다. 그리고 존재성이 확인이 된다면 어떠한 value를 가지고 있는지 확인하는 것이다. 0이 아닌 attribute value가 있다면 이는 중요하게 생각되어야 한다. 어떠한 두 문서를 비교한다고 했을 때도 아무리 많은 단어를 가지고 있더라고 존재하는 단어 그자체가 비교하는데 있어 중요하다는 것이다.
Critiques of the Attribute Categorization
- Incomplete
사실 지금까지 이렇게 category를 나눈다는 것은 완벽하지는 않다. 완벽할 수 없는데는 몇가지 이유가 존재한다. 몇몇 attribute는 asymmetric binary하고, 또 다른 attribute들은 cyclical 할 수도 있다. 이외에도 다음과 같은 이유들로 인하여 category를 나눈다는 것이 완벽할 순 없는 것이다.
- Asymmetric binary
- Cyclical
- Multivariate
- Partially ordered
- Partial membership
- Relationships between the data
- Real data is approximate and noisy
또한 현실 세계에서 data를 얻는다고 했을 때, 흔히 sensor로 data를 수집하는 경우에 data에 불필요한 noise가 존재할 수 있다. 그리고 현실로부터 sensor를 거쳐 원하는 pattern을 어떠한 방식을 사용해서 얻는데까지 무수히 많은 approximation 과정을 거치게 될 것이다. 각각의 단계에서 이전 단계의 결과를 완전히 그대로 받아들이지 않는다는 것이다. 특히 data 전체를 완벽하게 설명할 수 없어 대표적인 결과를 전달하는 것이 일반적이다.
Key Messages for Attribute Types
- The types of operations you choose should be "meaningful" for the type of data you have
위에서 살펴본 data의 property로는 distinctness, order, meaningful difference, meaningful ratio가 있고, 오로지 이 4가지만이 data의 property가 된다. 만약 data에 대해서 어떠한 operation을 하고자 할 때는 무엇을 하고 있는지 확실히 해야만 한다. 반드시 operation을 하고 싶은 data에 대해서 해당 data type을 알고 있는 상태로 올바른 operation을 적용해야 한다. 그리고 주로 현실에서 볼 수 이는 number나 string과 같은 data type들은 실제로 현실에 대해서 완벽하게 설명할 수 없고, 이는 오로지 이해를 위해서 변형된 형태임을 알아야 한다. 그래서 이러한 data type은 모든 것을 설명하기에는 어려움이 존재한다. 또한 분석을 하는 경우 data의 property가 어떠한 것인지에 따라 그 결과는 달라질 수 있으며, 예를 들어 많은 통계적 분석 방법의 경우 오로지 data의 분포에만 의존하게 된다. 마지막 중요한 내용으로는 meaningful 하다는 것은 특정 domain에 대해서만 구체화 될 수 있다는 것이다. 만약 어떠한 A라는 domain에 대해서 동작하는 것들이 B라는 domain에서는 동작하지 않게 되는 것이다. 사실 이러한 것이 data mining뿐만 아니라 machine learning에서도 문제가 되는 점들 중 하나이다. 그래서 더욱더 강력한 A.I.를 만들어야 하는 이유가 여기에 존재하게 되는 것이다.
이 세상에는 정말로 많은 task들이 존재하고 여기에 적용되는 A.I. 알고리즘들이 많이 존재한다. 특정 task에 적용이 되는 알고리즘이 다른 task에 대해서는 적용되지 않는 경우가 대부분이다. 이는 사람의 경우도 마찬가지이다. 누군가가 한 분야에 전문적인 지식이 있긴 하더라도, 모든 분야에 대해서 지식이 풍부하다는 것은 아니다. 현실 세계에서 우리는 어떻게든 data의 관점에서 모든 현상을 통합할 필요가 있다. 그리고 data는 컴퓨터가 이해할 수 있는 특정한 pattern을 찾기 위해 특별한 과정을 거쳐야 한다. 사실 이는 정말 어려운 과정이기 때문에 인간을 지배하는 A.I.를 보지 못하는 이유 중 하나로 작용될 수 있다.
