[데이터마이닝] Data and Data Preprocessing - Data Preprocessing

JAEYOON SIM·2022년 3월 3일

Data Mining

목록 보기

4/23

Data Preprocessing

Data quality와 관련된 여러 issue들을 해결하기 위해서 data preprocessing이 필요하다. Data preprocessing을 하게 되면 estimation이나 prediction task에서도 좋은 결과를 만들어 낼 수 있다. 대표적인 data preprocessing으로는 다음과 같이 존재한다.

Aggregation

Sampling

Discretization and Binarization

Attribute transformation

Dimensionality reduction

Feature subset selection

Feature creation

이제부터 하나씩 살펴보도록 하자.

1. Aggregation

Data aggregation은 2개 이상의 attribute나 object를 하나의 attribute나 object로 합치는 것을 말한다. Data aggregation을 하는 목적은 아무래도 data의 크기를 줄이는데 있다. Attribute나 object의 수를 줄이는 것이 data aggregation의 목적이고, 또 다른 목적이라고 하면 data의 scale을 바꾸고자 하는데도 있다.

Data reduction
Change of scale
More "stable" data

가령, city의 경우 region, state, country로 합칠 수 있는 것이고 day의 경우는 week, month, year로 합칠 수 있는 것이다. 결국에 이렇게 하는데는 우리가 더욱 stable한 data를 원하기 때문이다. Aggregated data는 변동성이 적은 경향이 있고, 결국 smoothing이라는 목적을 이루고자 하는 것이다. 대표적인 예시로 1982년부터 1993년까지 Austrailia의 강수량이 있다.
위 histogram은 하나는 월간 강수량의 평균을 표준 편차로 사용한 것이고 다른 하나는 연간 강수량의 평균을 표준 편차로 사용한 것이다. 표준 편차의 경우 data의 변동성을 포착하기 때문에 표준 편차가 작은 경우에는 data가 stable하다는 것을 의미하고 표준 편차가 큰 경우에는 data의 변동성이 크다는 것을 의미한다. 연간 평균 강수량의 경우 scale이 더 크기 때문에 월간 평균 강수량보다 더 적은 변동성을 기록하게 된다.

위의 histogram은 Austrailia를 여러 지역으로 나누고 강수량을 가지는 지역들이 얼마나 되는지를 설명하고 있다. 그래서 X축의 경우 표준 편차를 나타내기 때문에 값이 커질수록 해당 data에는 변동성이 커지게 된다. 반대로 표준 편차가 작은 좌측으로 갈수록 해당 data가 더욱 stable해지게 된다. 보다시피 연강 평균 강수량의 경우 표준 편차가 작은 쪽에 주로 분포하고 있어 더 stable한 것을 알 수 있다. Range, scale, resolution에 따라서 data는 안정성이 변하게 된다. 이러한 이유가 data agrregation의 이유가 되지만 여기서 더 중요한 점은 data dimension 관점에서 이득을 취할 수 있다. 이는 뒤에서 설명할 것이다.

2. Sampling

Sampling은 많고 많은 data 중에서 sample로서 사용할 것을 추출하는 것이다. 이렇게 되면 결과적으로 data의 크기를 줄일 수 있다. 즉, data reduction을 하기 위한 기법 중 하나가 sampling이다. 종종 data의 사전 조사와 최종 data 분석 모두에 사용된다. Sampling의 경우 2가지 관점으로 해석할 수 있다. 하나는 statistic의 관점이고 다른 하나는 data science의 관점이다. 엄밀히 이야기하면 두 관점은 다르지만 최근 들어 두 분야의 경계선이 사라지고 있는 경향이 있다.

Statistics - Obtaining

Statistics의 관점에서 sampling을 하는 이유는 관심 있는 data set 전체를 얻는 것이 너무 expensive하고 time consuming하기 때문이다. 예를 들어 우리가 특정 개수의 data를 얻어야 한다고 해보자. 이때 너무나도 많은 양의 data가 존재한다면 이를 모두 얻는데는 그만큼의 노력이 따를 것이다. 그래서 statistics의 관점에서는 모든 data를 사용하기 보다는 특정 개수의 data만을 sampling해서 사용하고 전체 data set을 추정하고자 하는 것이다.

Data science - Processing

Data science의 관점에서 sampling은 data mining에서 사용이 되는데, 그 이유가 관심 있는 data set 전체를 가공하는 것이 너무 expensive하고 time consuming하기 때문이다. Statistics의 경우 모든 data를 수집하기를 원하지 않았지만, data mining을 하는 사람들의 입장에서는 모든 data를 가공하기를 원하지 않는다.

사실 어디에 초점을 두는지가 그들만의 관점에서 차이가 있는 것이지만, 어찌됐든 효과적인 sampling의 주된 원칙은 동일하게 작용한다. 물론 모든 것을 편향되지 않게 유지하려면 random sampling을 해야하지만, 이는 다른 의미로 data analysis를 할 때 편향되게 sampling을 하게 되면 편향된 결과를 가져온다는 것을 의미한다. 만약 sample이 대표적이라면 sample을 사용하는 것은 전체 data set을 사용하는 것만큼 효과적이게 된다. 즉, sample만으로 전체를 대표할 수 있는 정보를 가질 수 있다면 굳이 전체 data를 사용할 필요는 없다는 것이다. 그리고 전체를 대표할 수 있는 sample이라고 하면 이는 원래의 data set과 거의 동일한 성질을 가진다는 것이다.

만약 random sampling을 통해서 시험지를 모아 채점을 했을 때 시험 점수가 모두 100점 중에 70점으로 동일하게 되면 이는 변동성이 0이 되어 이로인해 전체 인구의 시험 성적도 70점으로 추정할 수 있는 것이다. 어느정도 중간값을 sampling 하게 되면 이는 전체를 대표할 수 있지만, 만약 가장 높은 점수를 sampling 하게 되면 이는 대표할 수 있다고 말할 수 없게 된다. 그래서 sampling을 할 때에는 sampling한 data가 어느정도 대표할 수 있는 정보를 가지고 있어야 한다.

Sample Size

Sampling을 할 때 겨우 하나의 sample을 통해서 전체를 대표한다고 이야기할 수 없다. 반드시 충분한 개수의 sample을 통해서 전체를 대표하도록 해야한다.
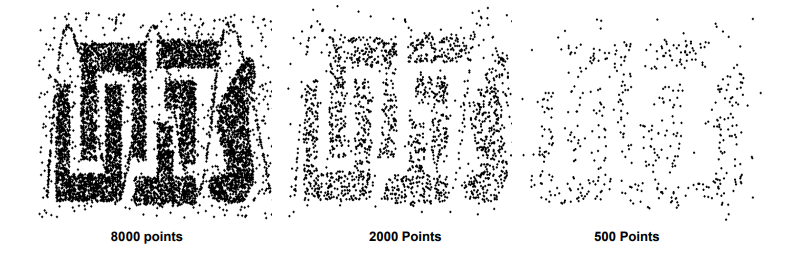위와 같이 2000개나 500개로는 충분히 data의 pattern을 설명할 수가 없다. 그래서 sampling을 할 때 충분한 개수를 통해서 전체를 대표해야 한다.
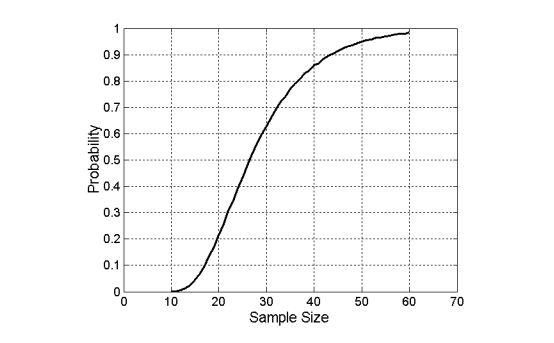충분한 sample size는 data에서 복잡한 pattern을 찾고자 할 때 반드시 필요하다. 위는 그저 하나의 예시로 sample size는 크기가 동일한 10개 그룹 각각에서 하나 이상의 object를 가져오는 것이 필요하다는 것을 설명하고 있다. 이 그룹들이 섞인 상태로 random sampling을 한다고 하면 적어도 10개 모두에서 하나 이상의 object를 sample로 뽑고 싶을 것이다. 위의 그래프는 모든 그룹에서 object를 뽑기 위한 sample size를 나타낸 것으로 약 60번의 sampling을 하게 되면 모든 그룹에서 object를 얻을 수 있다고 말하고 있다. 물론 운이 좋으면 10번만에 뽑을 수 있지만, 이는 확률적으로 희박하기도 하다.

Types of Sampling

1. Simple Random Sampling

아마 대부분이 생각하는 sampling이 simple random sampling일 것이다. 이 경우에 특정 item을 선택할 확률이 동일해야 한다. 여기서 핵심은 random sampling의 2가지 전략들이다. 예를 들어 1개의 바구니에 사과와 오렌지가 들어 있다고 가정해보자. 여기서 바구니 안에 있는 오렌지를 꺼낼 확률은 얼마나 될까? 이러한 경우에 꺼낸 과일을 다시 집어넣고 진행할 수도 있으며, 꺼낸 과일을 제외하고 진행할 수도 있을 것이다. 이 경우에서 보다시피 sampling을 할 때 sampling 된 결과를 전체에서 제외시킬 수도 있고 제외시키지 않을 수도 있다는 것이다. 아마 제외시키지 않으면 또 다시 sampling이 될 수도 있다. 그래서 이러한 sampling의 경우 동일한 sample이 또 다시 등장할 수 있고 이러한 경우가 duplicate data 문제를 발생시키는 것이다.

2. Stratified Sampling

Stratified sampling은 simple random sampling보다 더 중요하다. Stratified sampling은 data를 여러개의 partition들로 나눈 다음에 각 partition으로부터 random sampling을 하는 것이다. 그렇다면 왜 이렇게 하는 것일까? 만약 위와 같이 바구니 속 과일을 꺼내는 상황에서 오렌지와 사과의 개수가 달라 분포가 다른 경우에 sampling을 하게 되더라도 우리는 전체 모집단과 가능한 한 비슷한 비율을 유지하고자 하는 것이다. 이것이 의미하는 것은 사과를 어느정도 꺼냈다면 그만큼 오렌지도 꺼내서 기존의 비율을 유지하고자 하는 것이다. 우리가 stratified sampling을 할 때 결국에는 data label distribution을 유지하고자 하는 것이 이 sampling의 목적이다.

3.1. Discretization

Discretization은 continuous attribute를 ordinal attribtue로 변환하는 과정이다. 만약 해당 data가 continuous하다면 이를 구간별로 잘라서 동일한 category로 분류시킬 것이다. 예를 들어 시험 점수를 구간 별로 나눈 후에 학점을 부여하고자 하는 경우가 discretization에 해당한다. 그리고 discretization은 unsupervised와 supervised setting 모두에 사용될 수 있다.

Unsupervised Discretization

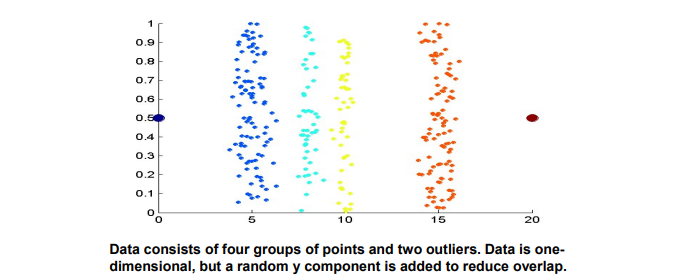위의 그래프는 4개의 색으로 구분되어져 있는 sample들을 나타낸 것이다. 그리고 각 그룹에서 sample의 수는 전부 다르고 여기서 하고자 하는 것은 ground truth를 색으로 구분한 4개의 그룹을 data mining을 통해서 그래프에 선을 그어서 나누고 싶은 것이다.
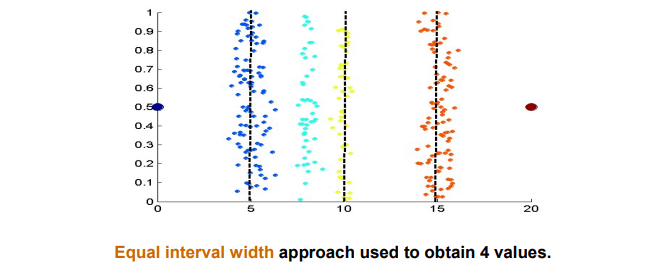만약 0에서 20까지의 범위에서 동일한 간격으로 4개의 구간으로 나누고자 한다면 위와 같은 결과가 나올 것이다. 나름 잘한 결과같지만 좋은 접근법은 아니다.
그렇다면 빈도로 나눈다면 어떠할까? 만약 총 100개의 sample이라고 한다면 25개씩 나눠서 4개의 구간으로 나누는 것이다. 이 또한 나름 괜찮은 결과를 보이는 것 같지만 이 또한 그리 좋은 접근법은 아니다.
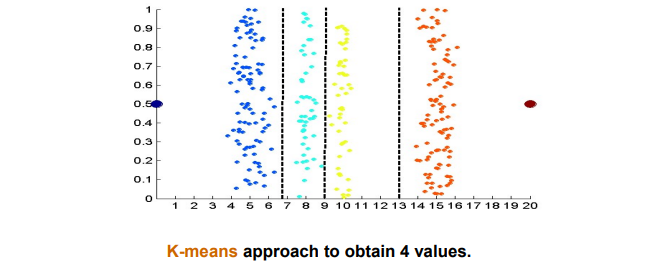그렇다면 K-means라는 기법을 통해서 접근하면 어떻게 될까? 이 경우 위와 같이 만족스러운 결과를 보여주는 것을 확인할 수 있다. K-means는 clustering의 일종으로 이렇게 접근하면 괜찮은 결과를 만들어낼 수 있다.

Supervised Discretization

Supervised discretiation에서는 특정 label을 주어진 상태로 그룹을 나누는 것이다. 위의 예시에서라고 하면 color 정보를 이미 알고 있는 상태로 discretization을 진행하는 것이다. 만약 정보를 미리 알고 있다면 classification task와 동일하게 되어 function을 학습해서 class label을 찾으면 될 것이다.

3.2. Binarization

Binarization은 discretization의 특별한 경우로, 오로지 2개의 category로 나누는 것을 말한다. Binarization은 continuous 혹은 categorical attribute를 하나 이상의 binary variable로 mapping한다. 이는 variable이 오직 0이나 1 중 하나를 택해야 하며, 만약 하나의 value만을 고려해야 한다면 그저 0이나 1을 택하면 되는 것이다. 그러나 다음과 같이 여러 선택지가 있는 경우에는 상황이 달라진다.
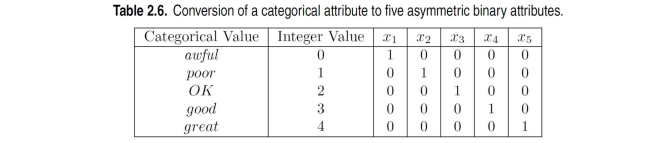위의 예시는 5개의 서로 다른 value를 attribute로 가졌을 때, 각각의 categorical value에 integer value를 할당한 것이다. 이렇게 해도 틀리지는 않지만, categorical value는 순서의 개념이 들어가있지 않아서 위와 같이 binary attribute로 바꿔줘야 한다.

4. Attribute Transformation

Raw data에 특정 function을 통해서 그 값을 바꾸는 것을 transformation이라고 한다. Attribute transformation은 각 old value를 new value 중 하나로 식별할 수 있도록 주어진 attribute의 전체 value의 집합을 새로운 대체 value의 집합에 mapping하는 function이다. 여기서 중요한 점은 raw data를 transformed data로 바꿀 수 있다면 역으로 transformed data를 raw data로도 전환할 수 있어야 한다. 간단한 예시로는 $x^k, \text{log}(x), e^x, |x|$ 등의 function을 사용할 수 있다. 보통 이러한 function들은 증가하거나 감소하는 경향을 보이기 때문에 대표적인 transformation function으로 사용된다. 그리고 linear function을 사용하게 되면 분석하는데 편하며, data를 쉽게 fitting 시킬 수가 있다. 그래서 $e^x$ 와 같은 function은 data set을 linear하게 만들고자 할 때 주로 사용한다.

또 다른 유명한 transformation으로 normalization이 있다. Normalization은 frequency occurrence, mean, variance, range 측면에서 attribute 간의 차이를 조정하는 다양한 기법을 말한다. Statistics에서는 normalization을 standardization이라고도 부르며, 이는 data로부터 mean을 빼고 standard deviation로 나누는 것을 말한다. 이는 평균을 0로 만들고 표준 편차를 1로 만드는 행위이며, data가 있을 때 이를 일반화시키고 싶을 때 사용하면 된다.

\text{Normalization in Statistics : Standardization} = X \rightarrow \frac{X-\mu}{\sigma}

5. Dimensionality Reduction

Curse of Dimensionality

Dimension reduction이 왜 중요한걸까? 그 이유는 바로 어떠한 A.I. 혹은 data science 분야에서도 생겨나는 curse of dimensionality 문제 때문이다. dimensionality가 증가하면 data는 공간 상에서 점점 sparse하게 되는 curse of dimensionality 문제가 생기고 이를 해결할 필요가 생긴다. 만약 data의 dimension이 너무 높은 경우에는 이를 characterization하기 어려워진다. 그리고 여기서 data의 dimensionality라는 것은 attribute의 개수를 의미한다.

그래서 만약 data의 dimension이 증가하게 되면, data는 아마 점점 sparse하게 변할 것이다. 예를 들어 2개의 attribute가 있다고 했을 때, data를 많은 sample로부터 얻게 되더라도 선택지는 2개뿐인 상황이 된다. 하지만 attribute가 100만개라고 한다면 동일한 sample이라고 하더라도 각각의 선택지가 100만개라 이는 비교할 수 없을 정도로 많은 시간이 소모될 것이다. 그리고 실제로 data를 얻는 과정에서 이렇게 많은 상황이 된다면 더 많은 zero value를 얻게 될 것이다. 계속해서 강조하는 부분이 오로지 non-zero value만이 의미가 있고 중요하다고 했다. 그렇기 때문에 data의 dimension이 증가할수록 data가 sparse해진다는 것이다.

그리고 attribute를 point로 나타낸다고 했을 때, clustering과 outlier detection에서 중요한 point 사이의 density와 distance에 대한 정의는 dimension이 증가할수록 그 의미가 줄어들게 될 것이다. 2차원에서는 쉽게 point 간 distance를 구할 수 있을 것이지만, dimension이 증가할수록 sparse해진 data에는 0이 많아져 어떠한 정보도 제공하지 못하는 지점이 많아질 것이다. 그렇기 때문에 attribute를 dimension의 관점에서 최대한 compact하게 하고 싶을 것이고, 최대한 많은 정보를 전달하고 싶을 것이다.

Asymmetric Attributes(revisited)

오로지 non-zero attribute value가 중요하다고 여겨지고, 이는 존재성의 큰 의의를 두고자 하는 것이다. 존재성을 이야기하고자 할 때 non-zero value를 통해서 이야기할 수 있다. 그리고 이러한 관점은 curse of dimensionality와 밀접한 관련이 있던 것이었다.

Dimensionality Reduction

Dimensionality reduction의 주된 목적 중 하나는 curse of dimensionality를 피하고자 하는 것이다. 또한, 엄청 큰 time complexity와 memory를 줄이는 것도 dimensionality reduction의 목적이다. 이외에도 data를 더 쉽게 visualization하고 관련이 없는 feature를 줄이고 noise를 없애는데 도움이 되기 때문에 dimensionality reduction을 하고자 하는 것이다. 아무래도 사람으로서 3차원 정도까지가 쉽게 받아들일 수 있는 범위이기 때문이다.

대표적인 dimensionality reduction 기법으로는 principal components analysis(PCA), singular value decomposition(SVD) 등이 있고, 이외에도 여러 기법들을 통해서 dimensionality를 줄일 수 있다. 대표적으로 discretization을 위한 K-means도 이러한 관점에서 사용된 기법이다. 이렇게 여러 기법들을 통해서 아무리 복잡한 data라도 2차원 등의 low dimension으로 만들어 쉽게 시각화할 수 있을 것이다.

6. Feature Selection

Feature selection 또한 data의 dimensionality를 줄이는 방법 중 하나이다. PCA의 경우 $x_1, x_2$ 라는 2차원의 data로부터 새로운 axis를 만들어서 dimensionality reduction을 수행하지만, feature selection의 경우에는 단순히 $x_1$ 과 $x_2$ 중에서 하나를 선택해서 dimensionality를 줄이게 된다. 여기서 어떠한 feature를 선택하는지에 대한 기준은 다양할 수 있지만, 일반적으로는 불필요하거나 관련이 없는 feature는 제외시키곤 한다. 불필요한 경우는 보통 많은 정보가 중복이 되는 경우이고, 관련이 없는 경우는 원하는 정보를 가지고 있지 않은 경우일 것이다.

그래서 PCA와 feature selection의 가장 큰 차이로 PCA는 결국에 새로운 feature dimension을 만들고자 하는 것이고, feature selection은 만들기보다는 기존의 것 중에서 선택하고자 하는 것이다. 그렇기 때문에 PCA의 경우는 machine learning algorithm에서 더 효과적일 것이다. 일반적으로 feature selection은 data science나 data mining에서 특정 feature를 선택해서 기존의 semantic를 잃지 않고자 할 때 주로 사용될 것이다.

7. Feature Creation

Feature creation은 data set의 중요한 정보를 원래 attribute보다 훨씬 효율적으로 설명할 수 있는 새로운 attribute를 만들어낸다. 이와 관련된 methodology로는 feature extraction, feature construction, mapping data to new space 등이 있고, 이 중에서 마지막에 mapping하는 경우에는 semantic을 잃어버리기 때문에 PCA와 밀접한 관련이 있다.

Feature extraction
Feature construction
Mapping data to new space

Mapping Data to a New Space

Fourier transform과 wavelet transform의 경우가 여기에 해당할 수 있다. Fourier transform은 data를 원래의 space에서 frequency space로 transformation 시키는 것이다. Frequency space로 변환하게 되면 noise가 사라지고 의미 있는 정보를 얻어내기 쉬워진다.
이렇게 Fourier transform을 통해서 우측의 frequency space를 보면 크게 올라와 있는 두 지점에서의 frequency component가 기존의 signal에서 가장 dominant한 attribute가 되는 것이다.

JAEYOON SIM

평범한 공대생의 일상 (글을 잘 못 쓰는 사람이라 열심히 쓰려고 노력 중입니다^^)