[데이터마이닝] Similarity and Dissimilarity - Distance Measures

Similarity and Dissimilarity

어떠한 두 가지가 비슷하다고 한다는 것은 만약 그것들을 quantification 할 수 있다면, 이들이 서로 다른지 아닌지도 quantification 할 수 있다. Similarity와 dissimilarity는 정반대의 것을 필요로 하지만 similarity를 측정하게 되면 이는 곧 dissimilarity를 측정하는 것으로 이어지게 된다. 반대의 경우도 성립하게 된다.

Measures

그렇다면 similarity와 dissimilarity는 각각 어떻게 나타낼 수 있을까?

1. Similarity Measure

Similarity measure는 두 data object들이 얼마나 유사한지를 나타내는 numerical measure이다. 예를 들어 오른손과 왼손이 각각 존재한다고 가정했을 때, 이들은 서로 다른 object이고 이들 사이의 similarity를 측정할 수 있을 것이다. 만약 similarity가 높게 나왔다면, data object들은 서로 유사함을 의미하게 된다. 하지만 그 값이 0에 가깝다면, object들은 서로 유사하지 않음을 의미하게 될 것이다. 그래서 일반적으로 similarity는 [0, 1]이라는 범위 내에서 설명하게 된다.

2. Dissimilarity Measure

Dissimilarity measure은 두 data obejct들이 얼마나 서로 다른지를 나타내는 numerical measure이다. 그렇기 때문에 similarity measure와는 반대로 그 값이 낮을수록 obejct들이 서로 유사하게 되는 것이다. 일반적으로 dissimilarity의 최소는 0이고, 최대는 제한 없이 얼마든지 커질 수가 있다. Similarity는 일반적으로 0과 1 사이에서 그 값이 형성되며 dissimilarity와는 반대되는 관계를 가지게 된다. 그래서 2개의 obejct가 매우 다른 상황을 반대로 생각하게 되면 아마 dissimilarity measure의 값은 무한대로 커질 것이고, 1을 넘어가게 되면 이는 similarity measure의 0과 같아지게 될 것이다.

3. Proximity

Proximity라는 용어는 상황에 따라 similarity를 나타낼 수도 있고, dissimilarity를 나타낼 수도 있다. 그래서 이 둘을 합쳐서 proximity라는 용어를 사용할 수 있다.

Simple Attributes

Data mining에서 2개의 data object가 있을 때, 우리는 data가 서로 어떻게 생겼는지 알 수가 있다. 예를 들어 data matrix가 있고, row는 data obejct가 있고 column으로는 feature가 있다고 해보자. 우리가 여기서 하고자하는 일은 특정 2개의 object의 similarity와 dissimilarity를 구하고자 하는 것이다.

Data mining에서 comparision은 정말로 중요한 개념이다. 왜냐하면 하나를 다른 것과 비교한다는 것은 자신을 제외한 유사한 cluster에서 유사한 data를 aggregation하는 방법에 대해서 말하고 있는 것과 같기 때문이다. 그렇기 때문에 similarity를 정의하는 것은 정말 중요하며, 여기에 필요한 것은 하나의 object가 다른 object와 얼마나 비슷한지에 대한 정보이다. 그렇다면 이러한 정보들을 어떻게 해서 알 수 있을까? 바로 attribute value들을 이용하면 된다.

Attribute value는 각 object를 설명할 수 있어서 attribute value를 통해서 각 attribute를 comparison에 사용하곤 한다.

1. Nominal

여기서 nominal attribute를 사용하게 되면 이를 통해서 오로지 object들이 같거나 다른지만을 설명하게 된다. 만약 같은 object라면 similarity는 1이 될 것이고, dissimilarity는 0이 될 것이다. 다른 경우에는 반대로 생각하면 될 것이다.

2. Ordinal

Ordinal attribute의 경우에는 2개의 object의 difference를 계산해서 $n-1$로 나누어 dissimilarity를 구하면 된다. 여기서 $n-1$로 나누는 이유는 $d$ 값을 적절한 값에 mapping하기 위해서다. 이와 다르게 similarity는 간단하게 1에서 dissimilarity 값을 빼주면 된다. Dissimilarity 값을 최종적으로 구하게 되면 값의 범위는 0에서 1 사이가 될 것이다. 그렇기 때문에 similarity는 1에서 빼주는 것이고, 이렇게 함으로써 ordinal simiailarity를 구하게 되는 것이다.

3. Interval / Ratio

마지막으로 interval과 ratio attribute의 경우에는 dissimilarity는 그저 두 object의 difference만 계산해주면 된다. 중요한 점은 이러한 방법이 유일한 거은 아니며, dissimilarity를 어떻게 구하는지에 따라서 이에 대응되게 similarity를 구해줄 수 있다. 그렇기 때문에 similarity와 dissimilarity의 경우 서로 inverse relation을 가지게 된다.

Euclidean Distance

그렇다면 어떻게 distance $d$를 정의할 수 있을까? 위에서 특정 attribute type에 따라 dissimilarity의 $d$를 구할 수 있었다. 이는 서로 다른 object의 difference를 계산한 것이었다. 결국 dissimilarity의 경우 data point들 사이의 distance라는 개념을 통해서 quantification 되어야 하고, 대표적인 Euclidian distance부터 알아보고자 한다. Euclidian distance는 distance를 구하는 방법 중에서 매우 유명하고 일반적인 metric 중 하나이다.

우리가 흔히 수학 시간에 배우는 2개의 point 사이의 길이를 Euclidean distance라고 한다. Data sample $x, y$가 $n$차원의 공간 상에 있을 때, 서로 대응되는 index간 차이를 구해서 제곱해서 더해준 뒤 결과적으로 root를 취하면 된다. Euclidean distance의 값이 커지게 되면 서로 다르다는 것이고, 반대로 값이 작아지게 되면 서로 유사하다는 의미가 된다. 이때 attribute value들의 경우 만약 scale이 다른 경우에는 standardization이 필수적이게 된다. 왜냐하면 attribute value가 다르다는 것은 일반적으로는 서로 다른 distribution을 형성하게 될 것이기에, scale을 맞춰서 standard normal distribution을 따르도록 standardization 과정이 동반되어야 한다.

위와 같이 4개의 서로 다른 point가 있다고 했을 때, 각 point 별로 distance를 측정할 수 있다. 여기서 point는 data object, $x$와 $y$는 coordinate를 attribute value로 가지는 attribute가 된다. 2차원에서 object들이 scatter point로 존재하고 있는 상태이고, distance matrix를 보면 각 object 사이의 distance가 기록되어져 있다. 여기서의 distance는 위에서 살펴 본 Euclidean distance를 사용했고, 각 point들을 연결한 길이를 symmetric하게 표기한 것이다.

Minkowski Distance

Minkowski ditance는 매우 중요한 개념으로 Euclidean distance를 일반화한 것이다.

여기서 $r$은 parameter로 만약 $r=2$라면, 위에서 살펴 본 Euclidean distance가 되는 것이다. 그렇다면 만약 $r\neq 2$이라면 어떻게 될까? 일반적으로 Euclidean distance를 자주 접해서 익숙해 보이지만, $r$의 값을 바꿔가게 되면 결국 다른 distance를 정의할 수 있게 되고 이것을 p-norm이라고도 한다. 예시 몇가지만 살펴보도록 하겠다.

만약 $r=1$이라면, Minkowski distance를 city block(Manhattan, taxicab, $L_1$ norm) distance라고 부를 수 있다. 여기서 $L_1$ norm은 p-norm 중에서도 p가 1인 경우를 말한다. 이러한 경우의 대표적인 예시로 binary vector를 대상으로 한 Hamming distance가 있고, 이는 그저 2개의 binary vector 사이에 다른 bit의 개수를 표현한 것이다.

만약 $r=\infty$라면, Minkowski distnace를 "supremum"($L_\text{max}$ norm, $L_\infty$ norm)이라고 부를 수 있다. 이는 vector로부터 component들 사이의 difference가 최대인 경우를 말한다. Vector로부터 모든 difference들을 살펴 볼 수 있는데, 여기서 각 element들이 maximum difference를 가지는 경우이다.

여기서 중요한 점은 우리는 $r$과 $n$을 동일한 것으로 착각하면 안된다. $r$은 그저 distance를 결정하는데 사용되는 parameter이며, 이는 모든 차원에서 정의되는 것이다. 그래서 $n$과는 상관없이 $r$은 어떠한 차원이라도 사용하고자 하는 distance measure에 따라 정의 될 수 있다.

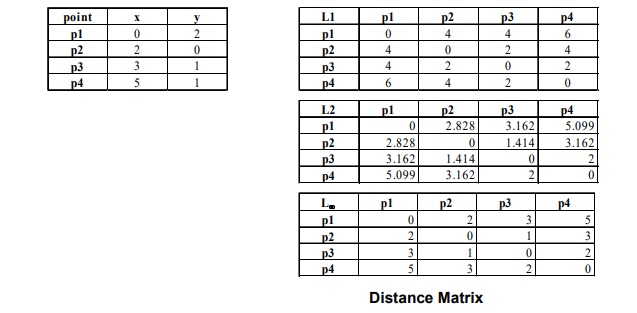이 예시에서 $x, y$는 coordinate로 attribute를 의미하고, p1, p2, p3, p4가 data object들이다. $L_1$ norm은 2개의 object간 distance를 가로와 세로로 이동했다고 생각하면 된다. 즉, 이 경우에는 각 axis를 따라서 그 값을 더해주기만 하면 된다. $L_2$ norm은 Euclidean distance이기에 제곱해서 더해준 후 루트를 계산해주면 된다. $L_\infty$ norm은 maximum difference이기 때문에 예를 들어 p1과 p3를 비교했을 때 $x$가 3이 차이나고 $y$가 1이 차이나서 그 값은 결국에 3이되는 것이다.

Mahalanobis Distance

Mahalanobis distance는 새로운 axis를 따라서 distance를 계산하게 된다. 그렇기 때문에 다음과 같이 식 중간에 covariance와 관련된 기호를 볼 수 있고, 그 기호는 바로 $\Sigma$로 이는 covariance matrix이다.

이 식이 말하고자 하는 것은 일종의 mapping 혹은 transformation이다. 우리의 data를 transformation 시켜서 알지 못하던 manifold로 이동시키게 된다. Mahalanobis distance도 결국 $x, y$의 difference를 측정하고자 하는 것이고, 이때 data간 covariance를 고려하게 된다.

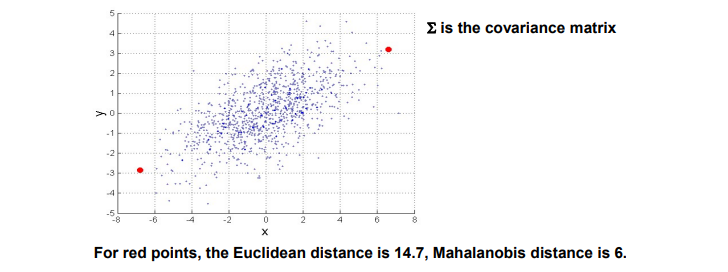만약 위와 같이 무수히 많은 data point 중에서 2개의 빨간 점 사이의 distance를 구하고 싶다면, $L_1$ norm이나 $L_2$ norm을 사용해도 상관이 없다. 그러나 만약 다른 data sample들이 존재하고 이들의 distribution을 알고 있다면, 이를 고려해서 p1과 p2 사이의 또 다른 distance를 구할 수 있을까? 우리가 앞서 이야기한 covariance matrix의 경우 data들이 밀접하게 관련이 있다면 이 또한 similarity measure로서 사용될 수 있다. 그렇기 때문에 data들의 distribution을 covariance matrix를 통해서 사용한다면 이로부터 $x$와 $y$가 similar한지 아닌지를 알 수 있을 것이다. 실제 distance가 멀리 떨어져 있다고 해도, covariance를 고려해주게 된다면 data가 어떻게 분포되었는지를 알 수 있어서 distance가 더 짧아질 수 있게 된다.

만약 위와 같이 빨간 점이 data distribution과 동일한 선상에 위치하지 않고 수직 방향에 위치하게 된다면 distance 크기는 어떻게 변할까? 비록 Euclidean distance가 동일하더라도 아무래도 covariance matrix를 이용하기 때문에 Mahalanobis distance가 엄청나게 커지게 될 것이다. 그래서 Mahalanobis distance의 핵심은 attribute space에서 2개 point의 distance를 구할 때 다른 data들의 distribution으로부터 relation을 고려해서 distance를 구한다는 것이다.

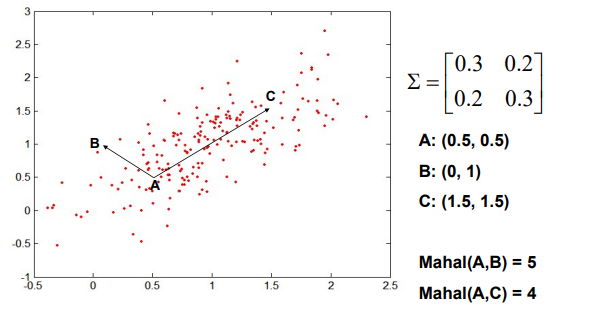위와 같이 A, B, C 3개의 point와 scattered point들이 분포하고 있고, 중심에 특히 더 많은 point들이 밀집되어 있는 것을 확인할 수 있다. 이때 covariance matrix는 $2\times 2$ matrix 이고 위와 같이 구할 수 있을 것이다. 각 point들의 coordinate가 위와 같을 때 Euclidean distance는 A와 C가 A와 B보다 더 클 것이다.

하지만 Mahalanobis distance의 경우는 다를 것이다. 왜냐하면 A와 C를 연결하는 방향으로 data sample들이 distribution을 형성하고 있기 때문이다. 그렇기에 covariance를 고려하게 된다면 A와 C의 관계가 더 가까운 것을 알 수 있다.

Common Properties

1. Distance

Eucliean distance와 같은 distance들은 잘 알려진 property들을 가지고 있다. $d(x,y)$를 2개의 data object $x,y$ 사이의 distance(dissimilarity)라고 한다면, distance는 다음과 같은 성질들을 만족하게 된다.

• (1) $d(x,y)\geq 0$ for all $x$ and $y$ and $d(x,y)=0$ if and only if $x=y$

• (2) $d(x,y)=d(y,x)$ for all $x$ and $y$. (Symmetry)

• (3) $d(x,z) \leq d(x,y)+d(y,z)$ for all points $x, y$ and $z$. (Triangle Inequality)

위 3가지 property를 만족하는 distance를 우리는 metric이라고 한다. 우리는 metric이란 것을 이용해서 무언가를 측정하는데 사용할 수 있다.

2. Similarity

Similarity 또한 잘 알려진 property들이 존재한다. Distance가 dissimilarity를 나타냈다면, 이번에는 그 반대되는 개념으로 similarity를 살펴보고자 한다. Similarity의 경우 2개의 object가 동일한다면 maximum similarity로 1의 값을 가지게 된다. 다시한번 차이점을 되새겨보면 similarity의 경우 maximum으로 1의 값을 가지지만, dissimilarity의 경우 maximum으로 $\infty$의 값을 가지게 된다. $s(x,y)$를 2개의 data object $x,y$ 사이의 similarity라고 한다면, similarity는 다음과 같은 성질들을 만족하게 된다.

• (1) $s(x,y)=1$ (or maximum similarity) only if $x=y$ (does not always hold, e.g. cosine)

• (2) $s(x,y)=s(y,x)$ for all $x$ and $y$. (Symmetry)