
Test Condition
Methods for Expressing Test Conditions
우리는 이전에 split을 하는 기준과 관련해서 이야기했었다. 그래서 자세하게 이야기하기 전에 먼저 attribute type에 대해서 다시 살펴보고 갈 것이다.
- Binary
- Nominal
- Ordinal
- Continuous
사실 이전에는 nominal, ordinal, interval, ratio attribute에 대해서 이야기 했었고, 이번에는 살짝 다른 컨셉으로 이야기해보고자 한다. Interval, ratio attribute는 continuous에 해당하게 되고, nominal이나 ordinal의 경우에서 binary case에 대해서 0 또는 1로 나타낼 수 있으면 binary attribute로 표현하고자 한다.
1. Nominal Attributes
Nominal attribute에 대해서 어떠한 것을 할 수 있을까? 사실 nominal attribute에 대해서는 의 경우나 의 경우만 우리가 이야기할 수 있다.
 만약 attribute가 3개의 value를 가지고 있다면, 우리는 가능한 attribute value들에 따라 multi-way branch를 만들 수가 있다. 아니면 3개 중 2개의 attribute를 묶어서 다음과 같이 2개의 branch로 만들 수도 있다.
만약 attribute가 3개의 value를 가지고 있다면, 우리는 가능한 attribute value들에 따라 multi-way branch를 만들 수가 있다. 아니면 3개 중 2개의 attribute를 묶어서 다음과 같이 2개의 branch로 만들 수도 있다.
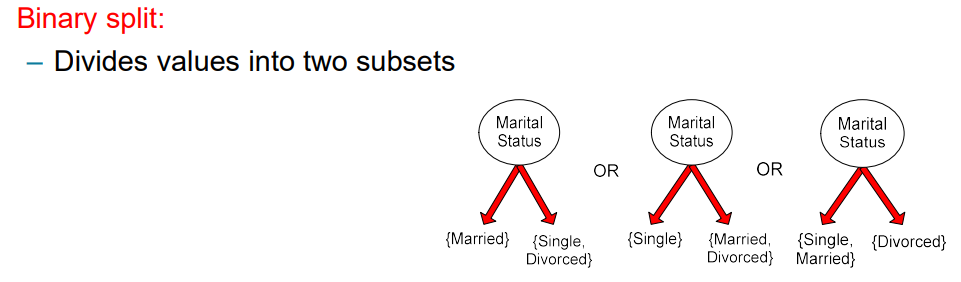 그렇게해서 만든 binary split의 경우는 어떻게 묶을지 조합에 따라 서로 다른 결과를 만들 수가 있다.
그렇게해서 만든 binary split의 경우는 어떻게 묶을지 조합에 따라 서로 다른 결과를 만들 수가 있다.
2. Ordinal Attributes
 Ordinary attribute의 경우에는 nominal attribute와 비슷하지만 차이점으로 순서가 존재하게 된다. 그래서 보통 일반적으로는 순서에 따라서 branch를 나누면 된다.
Ordinary attribute의 경우에는 nominal attribute와 비슷하지만 차이점으로 순서가 존재하게 된다. 그래서 보통 일반적으로는 순서에 따라서 branch를 나누면 된다.
 Nominal attribute와 마찬가지로 ordinal attribute 또한 여러개의 attribute를 묶어서 binary case로 만들 수가 있고, 또한 어떻게 묶을지 조합에 따라 서로 다른 결과를 만들어낼 수도 있다. 여기서는 일반적으로 순서가 존재하기 때문에 어느 지점에 threshold를 만들어 그 기준에 따라 2개의 set으로 나누게 된다. 사실 threshold를 정하지 않아도 되지만, 이렇게 나누는 것이 일반적인 방식이다.
Nominal attribute와 마찬가지로 ordinal attribute 또한 여러개의 attribute를 묶어서 binary case로 만들 수가 있고, 또한 어떻게 묶을지 조합에 따라 서로 다른 결과를 만들어낼 수도 있다. 여기서는 일반적으로 순서가 존재하기 때문에 어느 지점에 threshold를 만들어 그 기준에 따라 2개의 set으로 나누게 된다. 사실 threshold를 정하지 않아도 되지만, 이렇게 나누는 것이 일반적인 방식이다.
3. Continuous Attributes
Continuous attribute는 다소 다루기 어려울 수 있다. Continuous attribute의 경우에는 여러개의 bin들로 나눠야 한다. Discretization의 과정이 필요하고, 어느 지점이 가장 이상적인지 따져야 한다. 사실 threshold를 잘 설정해서 다음과 같이 binary split이나 multi-way split을 잘 해주면 된다.
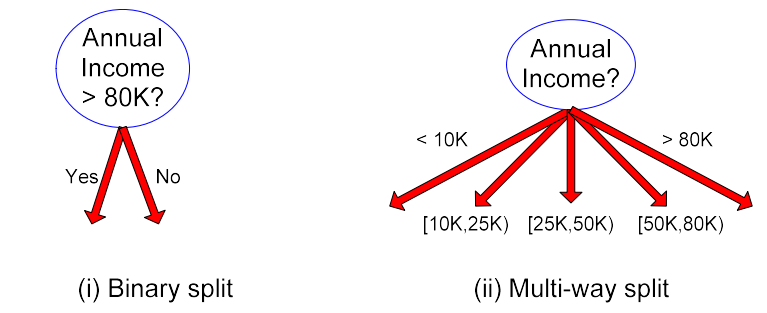
Splitting Based on Continuous Attributes
Continuous attribute를 나누는 것은 쉽지 않기 때문에 우리는 다음과 같이 여러 방법을 통해서 잘 나누려고 한다.
- (1) Discretization to form an ordinal categorical attribute
Range는 equal interval bucketing, equal frequency bucketing(percentiles), 혹은 clustering 등을 통해서 찾을 수 있다. Discretization criteria는 처음에 한번 진행이 되거나(Static), 각 node마다 반복될 수 있다(Dynamic). 우리는 항상 수많은 heuristic을 가지게 된다. 이러한 이유 때문에 너무나도 많은 decision tree algorithm들이 존재하는 것이다.
- (2) Binary Decision : or
여러개의 bin을 만들 수도 있지만, binary bin도 만들 수 있다. Threshold를 기준으로 크고 작고를 따지게 되면 결국에 continuous한 range를 2개로 나눌 수가 있다. 이러한 방식은 더 많은 연산이 필요할 수 있다. 왜냐하면 2개씩 나누게 되면 결국에는 정말로 많은 branch를 형성할 수 있기 때문이다. 4개로 한번에 나눌 수 있는 경우를 binary로 나누게 되면 6개를 계산해야 할 수도 있는 것이다. 그러나 binary의 장점은 그 구조가 정말 간단해져서 이해하는데 어려움이 없다는 것이다.
How to Determine the Best Split
지금까지 attribute의 종류에 따라 어떻게 split을 할 수 있는지에 대해서 알아보았다면, 이번에는 어떻게 최고의 split을 결정할 수 있을지에 대해서 알아보고자 한다. 다음과 같이 training data 가 있고, class label로 각각 10개씩 총 2개를 가지고 있는 경우를 보도록 하자. Custeomer ID, Gender, Car Type, Shirt Size까지 총 4개의 attribute가 있다.

If Gender?
만약 여기서 gender를 먼저 본다면 여기에는 male(M)과 female(F)로 총 2개의 경우가 존재한다. Male과 female로 나누게 되면 해당 branch에서 class label에 따른 distribution을 파악할 수 있다. 나름 잘 나눴다고 판단할 수도 있지만, 사실 잘 나눈 경우는 아닐 것이다.
If Car Type?
Car type으로 나누게 되면 gender보다 더 나은 결과라고 생각할 수 있다. 8개와 0개로 나뉜 node의 경우 leaf node가 확실시 된다. 1개와 7개도 꽤 나쁘지 않은 결과이고, 1개와 3개도 괜찮은 결과이다. 그래서 car type으로 data를 split하게 되면 gender보다 더 괜찮게 split을 했다고 판단할 수 있다.
If Customer ID?
마지막으로 customer id의 경우는 각각 1개씩 가지기 때문에 총 20개의 branch로 split 될 것이다. 당연히 각각을 branch로 나눴기 때문에 모두 1개와 0개의 경우를 가지게 될 것이다. 20개의 branch로 나눈 결과는 정말 완벽하다고 이야기할 수 있다. 그렇다고 각각을 하나씩 나누게 되는 것은 아무런 의미를 가지지 못할 것이다. 애초에 우리의 목적과는 다른 split 결과를 만든 셈이다. 우리는 처음부터 최소한의 branch로 최대한 완벽하게 class label을 나누고 싶었던 것이다. 그렇기 때문에 20개의 data object를 20개의 branch로 나누게 되면 높은 bias를 형성하게 될 것이다.
그래서 위의 예시에서 우리의 목적과 가장 부합한 것은 car type을 기준으로 split한 결과일 것이다.
 최적의 결과를 내기 위해서는 node가 pure해야 한다. 즉, purer class distribution이 있는 node를 선호하겠다는 이야기다. 위의 예시에서 좌측의 결과는 pure하지 못하고, 우측의 결과는 pure한 결과를 나타낸다. 그래서 좌측의 경우는 impurity가 높은 반면, 우측의 경우는 impurity가 낮다고 이야기할 수도 있다. 우리는 branch를 만들었을 때 classification을 하기 위해서는 해당 node에서 class label의 distribution이 한쪽으로 강하게 편향되기를 바란다.
최적의 결과를 내기 위해서는 node가 pure해야 한다. 즉, purer class distribution이 있는 node를 선호하겠다는 이야기다. 위의 예시에서 좌측의 결과는 pure하지 못하고, 우측의 결과는 pure한 결과를 나타낸다. 그래서 좌측의 경우는 impurity가 높은 반면, 우측의 경우는 impurity가 낮다고 이야기할 수도 있다. 우리는 branch를 만들었을 때 classification을 하기 위해서는 해당 node에서 class label의 distribution이 한쪽으로 강하게 편향되기를 바란다.
Measures of Node Impurity
그리하여 지금부터는 impurity를 quantification하고자 한다. Label의 distribution에 기반하여 우리는 impurity를 측정해야 하고, 여기에는 다음과 같이 3가지 방법이 존재한다. 각각을 설명하기 이전에 를 정의하고 시작하려고 한다. 는 node 에서 class 의 frequency를 나타내고, 는 class의 총 개수를 의미한다. 해당 node에서 각 class가 얼마나 나타나는지를 설명하기 위해서 확률적으로 정의한 것이다. 예를 들어, 총 3개의 class가 존재한다고 하고 각 class가 1, 4, 5개 존재하게 되면 각각 0.1, 0.4, 0.5의 확률을 가질 것이다. 그리고 이를 로 설명하겠다는 것이다.
1. Gini Index
Gini index는 각각의 확률을 제곱해서 다 더한 후에 1에서 그 값을 빼주는 식으로 계산된다. 그 이유는 만약 해당 node가 완벽하게 pure하다면, 하나의 만이 1이 되고 나머지는 0이 되어 결과적으로 1에서 1을 뺀 0이 될 것이다. Impurity가 0이 된다는 것은 purity의 관점에서는 완벽하다는 것이다.
만약 2개의 class가 각각 5개씩 있어 확률이 1/2라면 이로부터 Gini index는 1 - (1/4 + 1/4) = 1/2가 될 것이다. 그래서 class distribution이 impure 하다면 상대적으로 높은 값의 Gini index를 얻게 될 것이다. 반대로 class distribution이 pure 하다면 Gini index는 0에 가까운 값을 얻을 것이다.
2. Entropy
Gini index와 비슷한 것이 바로 entropy이다. 만약 class distribution이 pure한 경우에는 마찬가지로 하나의 class에 대해서만 가 1이 될 것이다. 이러한 경우에 값과 값 둘 중 하나는 각각의 경우마다 0이 생겨 전체적으로 entropy는 0이 될 것이다. 즉, impurity를 설명하기에 entropy를 사용할 수 있다는 것이다.
3. Misclassification Error
Misclassification error도 pure하면 0에 가깝고 pure하지 않으면 그 값은 커지게 될 것이다.
Finding the Best Split
Node 와 2개의 attribute 가 있을 때 어떠한 attribute를 선택해서 그것을 기준으로 split하면 될까? 만들 수 있는 경우는 2가지이고 각각에 대해서 split 이후에 class distribution에 대하여 impurity를 계산해보면 된다. 그리고 계산한 결과를 서로 비교해서 더 유용한 attribute를 선택하면 된다.
 차례대로 그 과정을 살펴보면 split 하기 이전에 node 에 대하여 impurity(P)를 계산해본다. 그리고는 각 경우에 대하여 split 이후에 impurity(M)를 계산해본다. 특히 각 child node에 대해서 impurity를 계산하게 되면 최종 M은 결국에 child node들의 weighted impurity가 될 것이다. 그리고는 가장 높은 gain을 만들어내는 attribute를 선택하면 된다. Gain은 다음과 같이 구할 수 있다.
차례대로 그 과정을 살펴보면 split 하기 이전에 node 에 대하여 impurity(P)를 계산해본다. 그리고는 각 경우에 대하여 split 이후에 impurity(M)를 계산해본다. 특히 각 child node에 대해서 impurity를 계산하게 되면 최종 M은 결국에 child node들의 weighted impurity가 될 것이다. 그리고는 가장 높은 gain을 만들어내는 attribute를 선택하면 된다. Gain은 다음과 같이 구할 수 있다.
이러한 과정이 최적의 split을 찾아내는 방법이 된다. 그럼 이제 예시를 통해서 살펴보도록 하자.
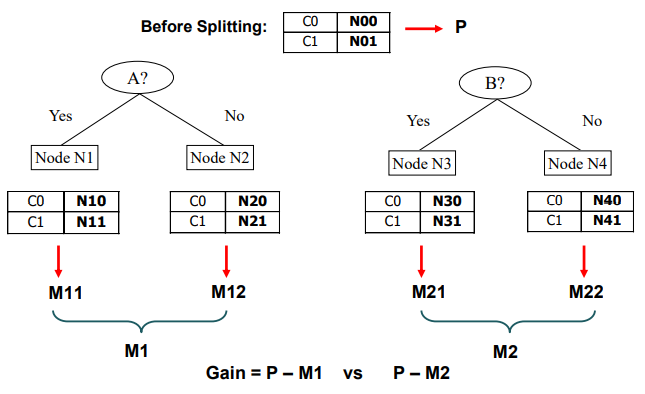 위와 같이 2개의 attribute 중에서 더 나은 attribute를 선택하기 위해서 와 각각의 을 구해서 gain을 비교하려고 한다. 여기서 핵심은 로부터 weighted summation을 통해서 을 만들고, 로부터 weighted summation을 통해서 를 만드는 것이다. Sample의 개수에 따라서 적절히 weight를 계산해야 한다.
위와 같이 2개의 attribute 중에서 더 나은 attribute를 선택하기 위해서 와 각각의 을 구해서 gain을 비교하려고 한다. 여기서 핵심은 로부터 weighted summation을 통해서 을 만들고, 로부터 weighted summation을 통해서 를 만드는 것이다. Sample의 개수에 따라서 적절히 weight를 계산해야 한다.
1. GINI
이제부터는 실제로 계산을 해보고자 하는데, 가장 먼저 Gini index부터 시작할 것이다. Gain을 구하는 방법 중에서 가장 먼저 Gini index를 사용할 것이다.
 Class가 2개일 때 하나의 class가 라는 확률을 가지면 나머지 class는 라는 확률을 가지는 것은 당연한 사실이다. 위와 같이 class label distribution이 존재하는 경우들로부터 각각 Gini index 값을 계산할 수가 있다. 이전에 살펴보았다시피 0.5의 확률을 가지는 경우가 가장 impurity한 경우에 해당하게 된다.
Class가 2개일 때 하나의 class가 라는 확률을 가지면 나머지 class는 라는 확률을 가지는 것은 당연한 사실이다. 위와 같이 class label distribution이 존재하는 경우들로부터 각각 Gini index 값을 계산할 수가 있다. 이전에 살펴보았다시피 0.5의 확률을 가지는 경우가 가장 impurity한 경우에 해당하게 된다.
Computing GINI Index for a Collection of Nodes
Node들로부터 Gini index를 구하고자 하는데, 특히 하나의 parent node로부터 child node가 여러개 있을 때 한번에 구하고자 한다. Node 가 개의 partition 혹은 children으로 split이 된다면 다음과 같이 Gini 값을 한번에 구할 수 있다. 각 child node로부터 Gini index를 구해서 weighted summation을 통해서 구하는 것이다. 사실 전체 구조를 살펴보면 weighted mean의 구조를 보이고 있다. 즉, expectation과 같은 구조를 보이는 것이다.
1.1. Binary Attributes: Computing GINI Index
Binary attribute에 대해서 Gini index를 구하는 예시를 보도록 하자. Binary attribute이기 때문에 2개의 child node를 가지게 된다.
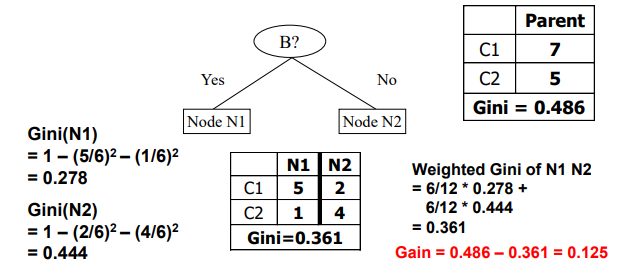 먼저 parent node의 class distribution이 7:5라고 해보자. 이 경우에 Gini index는 0.486으로 계산될 것이다. 그리고 이를 2개의 child node로 나누고 class distribution을 보면, 각각 5:1과 2:4로 형성되는 것을 확인할 수 있다. 각 경우로부터 Gini index를 구하면 0.278과 0.444가 나올 것이고, 여기에 각 sample 개수에 따른 weight를 부여해주면 최종적으로 0.361이라는 Gini index 값을 얻을 것이다. 따라서 최종적으로 gain은 0.486에서 0.361을 뺀 0.125가 될 것이다.
먼저 parent node의 class distribution이 7:5라고 해보자. 이 경우에 Gini index는 0.486으로 계산될 것이다. 그리고 이를 2개의 child node로 나누고 class distribution을 보면, 각각 5:1과 2:4로 형성되는 것을 확인할 수 있다. 각 경우로부터 Gini index를 구하면 0.278과 0.444가 나올 것이고, 여기에 각 sample 개수에 따른 weight를 부여해주면 최종적으로 0.361이라는 Gini index 값을 얻을 것이다. 따라서 최종적으로 gain은 0.486에서 0.361을 뺀 0.125가 될 것이다.
Parent node의 경우 매우 impure하고 uncertain한 것을 Gini index로 확인했었다. 왜냐하면 Gini index의 maximum 값은 0.5이기 때문이다(뒤에서 확인 가능). 하지만 child node의 impurity를 계산하게 되면 Gini index 값이 줄어든 것을 볼 수 있다. 이에 따라 gain 값이 결정이 되었고, 이로부터 우리는 0.125 gain만큼 도움이 되었다고 이야기할 수 있다. 만약 또 다른 경우에 대해서 gain을 구했다면, 그 값들을 비교해서 가장 큰 gain의 경우를 선택하면 된다.
1.2. Categorical Attributes: Computing GINI Index
만약 attribute의 type이 categorical attribute라면, 오직 2개의 object가 같은지 다른지만을 이야기할 수 있다. 그래서 우리는 오로직 얼마나 많은 attribute가 같은지 혹은 다른지에 대한 개수를 counting하기만 할 수 있다. 그래서 다음과 같이 car type을 branching한다고 하면 family, sports, luxury로 나누게 되는 것이다.
 그리고 이를 좌측과 같이 3개의 branch로 나누고 그 결과를 살펴보게 되면 sports car는 100% 잘 되었고 luxury car도 거의 90%로 잘 되었지만 family car를 보면 1개의 error이지만 75%이기에 잘 되었다고 이야기하기엔 살짝 애매하다. 그래서 좌측과 같이 하나씩 branch로 나눌 수도 있지만, 우측과 같이 2개의 branch로 묶을 수도 있다. 그래서 3개의 branch 중에서 2개를 함께 고려할 것이다. 하지만 어느 것을 묶을지 잘 선택해야하며, sports car와 luxury car를 묶게 되면 Gini 값이 0.468로 거의 의미가 없는 상황이 되어버리게 된다. 3개의 branch의 결과보다도 훨씬 좋지 않은 결과를 보일 수 있다는 것이다. 가장 우측과 같이 family car와 luxury car를 묶어버리면 마찬가지로 3개의 branch보다도 Gini 값이 살짝 높은 것을 볼 수 있다. 하지만 이정도 차이의 Gini 값일지라도 branch의 개수가 3개보다는 2개로 나누는 것이 더 간단한 tree를 만드는 상황을 연출하게 되는 것이다. 사실 이는 만드는 사람의 의도가 가장 중요하다. Gini 값이 살짝 높더라도 branch의 개수를 줄여 더 간단한 tree를 만들 것인지, 아니면 branch의 개수가 3개더라도 Gini 값을 낮게 만들 것인지는 tree를 만드는 사람의 의도에 달려있다. 그래도 일반적으로는 어느정도 Gini 값이 낮다고 생각하면 branch의 개수를 적은 쪽을 선택할 것이다.
그리고 이를 좌측과 같이 3개의 branch로 나누고 그 결과를 살펴보게 되면 sports car는 100% 잘 되었고 luxury car도 거의 90%로 잘 되었지만 family car를 보면 1개의 error이지만 75%이기에 잘 되었다고 이야기하기엔 살짝 애매하다. 그래서 좌측과 같이 하나씩 branch로 나눌 수도 있지만, 우측과 같이 2개의 branch로 묶을 수도 있다. 그래서 3개의 branch 중에서 2개를 함께 고려할 것이다. 하지만 어느 것을 묶을지 잘 선택해야하며, sports car와 luxury car를 묶게 되면 Gini 값이 0.468로 거의 의미가 없는 상황이 되어버리게 된다. 3개의 branch의 결과보다도 훨씬 좋지 않은 결과를 보일 수 있다는 것이다. 가장 우측과 같이 family car와 luxury car를 묶어버리면 마찬가지로 3개의 branch보다도 Gini 값이 살짝 높은 것을 볼 수 있다. 하지만 이정도 차이의 Gini 값일지라도 branch의 개수가 3개보다는 2개로 나누는 것이 더 간단한 tree를 만드는 상황을 연출하게 되는 것이다. 사실 이는 만드는 사람의 의도가 가장 중요하다. Gini 값이 살짝 높더라도 branch의 개수를 줄여 더 간단한 tree를 만들 것인지, 아니면 branch의 개수가 3개더라도 Gini 값을 낮게 만들 것인지는 tree를 만드는 사람의 의도에 달려있다. 그래도 일반적으로는 어느정도 Gini 값이 낮다고 생각하면 branch의 개수를 적은 쪽을 선택할 것이다.
1.3. Continuous Attributes: Computing GINI Index
Categorical attribute와는 다르게 continuous attribute의 경우에는 단순하게 숫자로 되어있기 때문에 그저 비교만하면 된다. 하나의 값을 기반으로 binary decision을 사용하면 되고, 여기서 binary decision이 의미하는 바는 thresholding을 의미한다. 기준 값을 기반으로 이 값보다 큰지 아니면 작은지로 나타내는 것이다. Continuous attribute는 간단하지만 여기서 threshold 값을 적절하게 잘 정해주는 것이 중요하다. 그리고 continuous attribute의 경우에는 어떠한 값을 선택하기에 따라서 branch의 개수가 여러개가 될 수 있다. 그렇기 때문에 적절한 threshold 값을 찾는 과정이 정말로 중요하게 작용할 것이다. Tree를 정말 간단하게 만들고 싶으면 하나의 threshold를 잘 정해서 이 값보다 큰지 아니면 작은지로만 나눠주면 된다.
그리고 항상 그래왔듯이 적절한 threshold 값 를 찾는 방법들이 존재한다. Continuous attribute를 가지는 data sample들이 개가 존재한다고 해보자. 간단한 방법으로는 각각의 후보들에 대해서 database를 살피면서 count matrix를 얻은 뒤에 Gini index를 계산하는 것이다. 이는 정말 단순하게 여러 를 가지고 다 계산해서 비교하겠다는 것이기 때문에 computation 관점에서 정말 비효율적이다.
 예를 들어 위와 같이 값을 80으로 정하고 이로 인한 count matrix를 나타낸 것이다. 이는 하나의 값에 대해서 만든 결과이고, 여러 들에 대해서 이렇게각각의 count matrix를 만들어야 하는 비효율적인 계산이 추가적으로 필요하게 된다. 각 count matrix마다 Gini index를 계산할 수 있고, 이들의 값을 비교함으로써 어떠한 threshold가 최적인지를 결정할 수 있다.
예를 들어 위와 같이 값을 80으로 정하고 이로 인한 count matrix를 나타낸 것이다. 이는 하나의 값에 대해서 만든 결과이고, 여러 들에 대해서 이렇게각각의 count matrix를 만들어야 하는 비효율적인 계산이 추가적으로 필요하게 된다. 각 count matrix마다 Gini index를 계산할 수 있고, 이들의 값을 비교함으로써 어떠한 threshold가 최적인지를 결정할 수 있다.
2. Entorpy
이번에는 또 다른 impurity measure인 entorpy에 대해서 알아볼 것이다.
Record들이 모든 class에 대해서 동일하게 분포하고 있다면, entropy의 최대값은 가 된다. 예를 들어, 2개의 class 에 대해서 각각이 5개씩 동일하게 존재하는 경우를 이야기하는 것이다. 즉, class가 2개인 상황에서 Entropy의 최대값은 이 되는 것이다. 만약 class가 3개라면, entorpy의 최대값은 이 될 것이다. 이렇게 동일하게 분포되어 있는 상황은 classification에 있어서는 별로 도움이 되지 않는다.
반대로 모든 record들이 하나의 class에 잘 속하고 있다면, entropy의 최소값인 0이 될 것이다. 그리고 이는 classification에서는 가장 필요한 상황을 의미하게 된다.
Computing Information Gain After Splitting
Gini index와 마찬가지로 split 이후에 entropy를 이용하여 Gain을 구하고자 한다면 다음과 같이 계산할 수 있다. Parent node 를 개의 partition(children)으로 나누는 상황이다.
Parent node의 entropy와 children node들의 entropy들의 weighted summation을 한 것의 차이를 통해서 Gain을 구할 수 있다. 그리고 이렇게 구한 Gain을 Information Gain이라고 한다. 우리는 Gain을 최대로 얻기 위해서 가장 많이 줄일 수 있는 split을 선택해야 한다. 그리고 이러한 것들은 ID3나 C4.5와 같이 유명한 decision tree algorithm들에 사용이 된다. 또한 이러한 information gain은 class variable과 splitting variable 사이의 mutual information으로 보기도 한다.
Problem with Large Number of Partitions
이번에는 partition을 많이 가져가게 되면 생기는 문제점에 대해서 생각해보려고 한다.
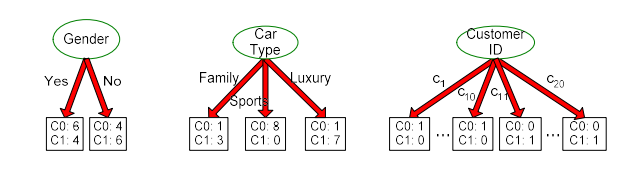 하나씩 다시 살펴보면 gender와 같이 나눈 경우에는 결과 자체가 문제가 많음을 알 수 있다. 2개의 children node 모두 거의 50%에 가깝기 때문에 impurity가 굉장히 높다. 반면, car type은 완벽하진 않아도 가장 괜찮은 결과를 보이고 있다. 마지막은 이미 위에서 봤지만, 각 record에 대해서 하나의 branch를 할당하게 되면 완벽한 결과를 얻게 되지만 이는 decision tree로서 의미가 없다고 이야기 했었다. Customer ID는 모든 children에 대해서 entropy 값이 0이기 때문에 가장 높은 information gain 값을 얻을 것이다. 이는 완벽하게 pure하지만 새로운 data에 대해서는 제대로 동작하지 못할 것이다.
하나씩 다시 살펴보면 gender와 같이 나눈 경우에는 결과 자체가 문제가 많음을 알 수 있다. 2개의 children node 모두 거의 50%에 가깝기 때문에 impurity가 굉장히 높다. 반면, car type은 완벽하진 않아도 가장 괜찮은 결과를 보이고 있다. 마지막은 이미 위에서 봤지만, 각 record에 대해서 하나의 branch를 할당하게 되면 완벽한 결과를 얻게 되지만 이는 decision tree로서 의미가 없다고 이야기 했었다. Customer ID는 모든 children에 대해서 entropy 값이 0이기 때문에 가장 높은 information gain 값을 얻을 것이다. 이는 완벽하게 pure하지만 새로운 data에 대해서는 제대로 동작하지 못할 것이다.
Gain Ratio
결국 마지막에 정의하는 것은 Gain ratio이다. Gain ratio는 우리가 사용하는 Gain인 이나 을 로 나눠준 것이고 이는 다음과 같다.
만약 branch의 개수가 많으면 많을수록 의 값이 증가할 것이다. 반대로 branch의 개수가 적으면 적을수록 그 값은 감소할 것이다. 위의 예시를 다시 보면 customer ID에 대해서 20개의 sample과 20개의 branch의 경우 그 값을 대입해보면 값이 총 20번 더해지게 되는 셈이다. Car type의 경우에는 3개의 node에 4 / 8 / 8로 나눈 것을 볼 수 있고, 이를 대입해보면 가 될 것이다. 이렇게 계산한 2개의 를 비교해보면 branch가 20개인 경우가 branch가 3개인 경우보다 더 큰 값을 가지는 것을 확인할 수 있다. 그리고 branch가 많아져 커진 는 결국에는 gain ratio를 작게 만들 것이다.
그리고 식을 자세히 보면, 결국 entropy와 다를게 없다. 만약 branch가 많아지게 되면, uncertainty가 증가하게 된다. 그리고 우리는 이러한 partitioning의 entropy 값을 통해서 information gain을 조절할 수가 있는 것이다. 기존의 information gain과 같은 것을 통해서 attribute를 선택할 수 있겠지만, 여기에 를 통해서 최종적으로 얻는 Gain을 조정하여 그 비율로서 우리는 정보를 얻겠다는 것이다. 이러한 식을 통해서 우리는 많은 branch로 인하여 생기는 information gain의 단점을 극복해보고자 하는 것이다.
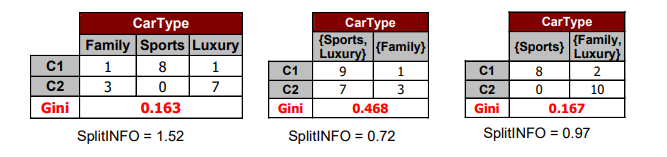 다시 위의 예시를 통해서 그 결과를 비교해보도록 하자. 첫번째는 3 way branching이고 나머지 2개는 2 way branching을 한 것이다. 처음에 이 예시에서는 3번째 상황이 그저 Gini index가 낮고 branch의 개수가 2개라서 더 간단하기에 이를 선호한다고 이야기 했었다. 이제는 gain ratio라는 식을 알게 되었고, 이를 통해서 더욱 그 이유가 명백해진 것이다. 추가적으로 값을 보면 확실하게 3번째 경우가 첫번째 경우보다 더 낮아서 전체적으로 gain ratio의 값이 차이가 생긴 것을 확인할 수 있다.
다시 위의 예시를 통해서 그 결과를 비교해보도록 하자. 첫번째는 3 way branching이고 나머지 2개는 2 way branching을 한 것이다. 처음에 이 예시에서는 3번째 상황이 그저 Gini index가 낮고 branch의 개수가 2개라서 더 간단하기에 이를 선호한다고 이야기 했었다. 이제는 gain ratio라는 식을 알게 되었고, 이를 통해서 더욱 그 이유가 명백해진 것이다. 추가적으로 값을 보면 확실하게 3번째 경우가 첫번째 경우보다 더 낮아서 전체적으로 gain ratio의 값이 차이가 생긴 것을 확인할 수 있다.
이러한 이유 때문에 branch의 개수가 적은 것이 더 간단한 tree를 만들기 때문에 선호하게 되는 것이고, 이는 Ocam's Razor에 기반한 내용이기도 하다. 를 이용해서 gain을 조정하는 과정이 우리에게 더 간단한 model을 선택하는데 도움을 줄 수 있다.
3. Classification Error
Impurity measure의 마지막 방법으로 classification error를 알아볼 것이다.
만약 class label이 5개, 5개가 존재한다면, 각각의 probability는 0.5일 것이고 이들 중 최대값을 선택해서 1에서 빼주겠다는 것이다. 만약 6개, 4개가 존재하면 각 probability는 0.6, 0.4가 될 것이기에 이중에서 0.6을 1에서 빼주면 된다. 그렇기 때문에 만약 완전히 pure한 상황이면 1에서 1을 빼주기에 error 값은 0이 되어 최소가 될 것이다. 반대로 상황이 매우 uncertain하다면 각각의 probability가 모두 동일하게 될 거이고, 이는 결국에 1에서 class 개수의 역수를 빼준 것과 같아질 것이다. 그리고 이 값은 곧 classification error의 최대가 될 것이다.
Comparison
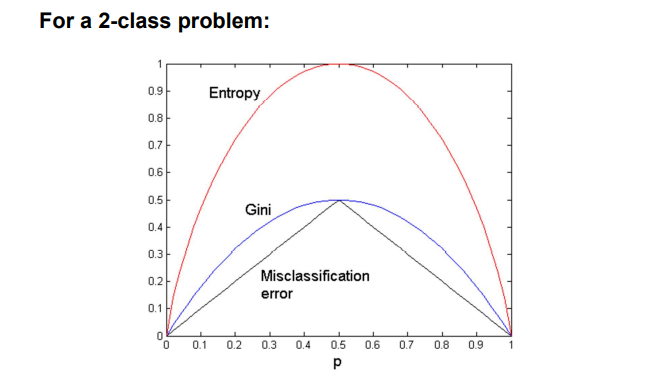
지금까지 알아본 3개의 impurity measure 각각의 binary problem에서의 값은 다음과 같을 것이다. 3개 모두 완전히 확실한 경우에 대해서는 그 값이 전부 낮은 것을 확인할 수 있다. 반면, 반반의 경우에는 impurity 모두 최대치를 기록하는 것을 볼 수 있다.
Pros and Cons of Decision Tree Based Classification
지금까지는 최적의 split을 위해서 어떠한 방법들을 사용하는지 알아보았다. 이제는 decision tree를 기반으로 classification을 할 때의 장점과 단점이 어떠한지 생각해보고자 한다.
Advantages
- 먼저 decision tree를 사용한다는 것은 상대적으로 classfier를 만드는데 수고가 적은 편이다. Decision tree에서는 오로지 node impurity를 계산하는 일만 하면 된다. Split을 통해서 얻는 information gain이 얼마나 되는지 비교만 하기 때문에 상대적으로 수고가 적은 algorithm에 속한다.
- Decision tree는 전혀 알지 못하는 새로운 record들에 대해서 정말 빠른 속도로 classification이 가능하다. 새로운 data가 등장하면 그저 만들어 놓은 tree를 따라 내려가기만 하면 되기 때문이다.
- Decision tree는 해석하는데 어려움이 없다. 왜냐하면 attribute를 기반으로 split을 하기 때문이다. 그렇기 때문에 model이 어떠한 것을 하는지 쉽게 이해할 수 있다.
- Class label의 distribution을 고려하기 때문에 noise에 robust하다. 비록 noise가 존재하는 경우가 있다고 하더라도 impurity measure에 기반하여 split을 했기 때문에 크게 상관하지 않아도 된다.
- Decision tree는 불필요하고 관련이 없는 attribute를 쉽게 다룰 수가 있다. 비록 1000개의 attribute를 다룬다고 할지라도 3번의 split만으로도 충분한 학습이 가능하여 classfication을 잘 수행할 수 있다. 즉, 1000개의 attribute 중에서 3개만으로도 classfication이 가능하다는 것이다.
Disadvantages
Decision tree는 현재 시점에서 가장 적절한 선택을 하는 greedy algorithm이기 때문에 미래를 전혀 고려하지 않는다. 그렇기 때문에 현재의 split 상태가 global optimum인지 아닌지 알 수가 없다. 그리고 greedy algorithm이기에 또한 class를 함께 구분할 수 있지만 개별적으로 구분할 수 없는 interacting attribute는 덜 구별되는 다른 attribute로 대체될 수 있다. 즉, single attribute가 좋은 attribute가 아닐지도 모른다는 이야기다. 이들은 2개의 attribute를 곱한다거나 해서 함께 사용하게 되면 좋은 attribute가 될 수도 있다. 그리고 각각의 decision boundary가 오로지 single attribute에 관여하게 된다.
Handling Interactions
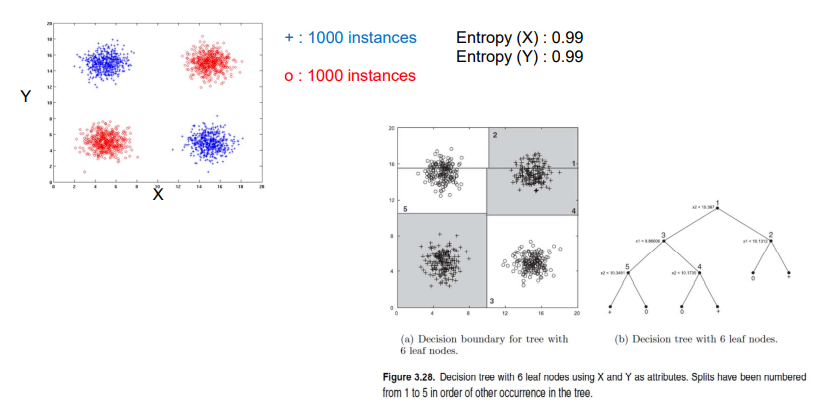 위와 같이 각각 1000개의 plus instance들과 circle instance들이 존재한다고 해보자. 그리고 class 모두 entropy가 0.99라고 해보자. 그러면 우측과 같이 decision tree를 만든다고 했을 때, 각각의 번호에 대응하는 decision boundary를 그려가면서 classification을 하고자하는 것이다.
위와 같이 각각 1000개의 plus instance들과 circle instance들이 존재한다고 해보자. 그리고 class 모두 entropy가 0.99라고 해보자. 그러면 우측과 같이 decision tree를 만든다고 했을 때, 각각의 번호에 대응하는 decision boundary를 그려가면서 classification을 하고자하는 것이다.
우측의 branch의 경우에는 data의 상단 부분만을 고려해서 classiciation 하겠다는 이야기고, 좌측의 branch의 경우에는 data의 하단 부분을 다시 세밀하게 고려해서 classification 하겠다는 이야기다. 이러한 식으로 decision boundary를 통해서 부분부분을 classification할 수가 있다. 사실 중간을 기준으로 십자가 모양으로 decision boundary를 그릴 수 있겠지만, entropy라는 이유 때문에라도 여러 branch로 나눠가면서 classification을 해야하는 것이다. Split이 많아질수록 공간 상의 decision boundary는 더 많아질 것이다. 우리는 위와 같이 2차원에서는 서로의 axis에 수직인 decision boundary를 계속 그려나가면서 classfication을 하게 된다. Decision tree에서 이는 매우 중요한 특징으로 결국에는 decision boundary가 계단과 같은 모양으로 생겨나가게 되고, 여기서 문제는 이러한 이유가 interaction을 다루지 못하게 결정적인 원인이 되는 것이다. 이에 대해서 조금 더 디테일하게 알아보도록 하자.
Handling Interactions given Irrelevant Attributes
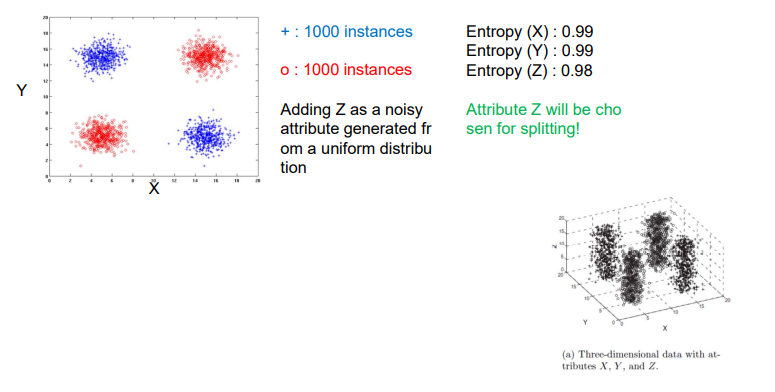 우리는 기존의 2개의 axis에 하나의 axis를 추가할 것이다. 여기서 추가된 axis 는 uniform distribution으로부터 생겨난 noisy attribute이다. 이를 visualization하면 위와 같이 하나의 차원이 추가된 것을 확인할 수 있다. 는 그저 noise이지만 split을 위해서 함께 선택이 될 것이고, 기존의 의 entropy를 통해서 uncertainty가 분명히 존재했다. 그리고 이보다 약간 작은 entropy 값을 도 가지게 된다고 했을 때, 우리는 또한 마찬가지로 split을 하는데 선택하는 것을 원하지 않을 것이다. 그래서 이러한 종류의 decision tree는 irrelevant attribute를 다루지 못하는 문제가 생기게 된다. 그렇기에 이 또한 문제점이 될 수 있다.
우리는 기존의 2개의 axis에 하나의 axis를 추가할 것이다. 여기서 추가된 axis 는 uniform distribution으로부터 생겨난 noisy attribute이다. 이를 visualization하면 위와 같이 하나의 차원이 추가된 것을 확인할 수 있다. 는 그저 noise이지만 split을 위해서 함께 선택이 될 것이고, 기존의 의 entropy를 통해서 uncertainty가 분명히 존재했다. 그리고 이보다 약간 작은 entropy 값을 도 가지게 된다고 했을 때, 우리는 또한 마찬가지로 split을 하는데 선택하는 것을 원하지 않을 것이다. 그래서 이러한 종류의 decision tree는 irrelevant attribute를 다루지 못하는 문제가 생기게 된다. 그렇기에 이 또한 문제점이 될 수 있다.
Limitations of Single Attribute-Based Decision Boundaries
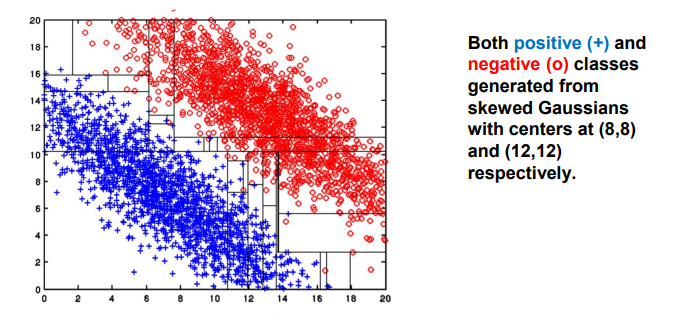 Single attribute-based decision boundaries의 또 다른 limitation은 decision boundary가 수직으로 형성할 수 없다는 것이다. 아무래도 위와 같은 data distribution에서 가장 이상적인 decision boundary는 우하향하는 대각선으로 그려야할 것이다. 하지만 이는 현실적으로 불가능하기에 실제로는 이에 근사하는 계단 모양으로 여러 decision boundary가 합쳐진 상태로 만들 수 있다. 이러한 이유는 decision boundary가 각각의 axis에 수직으로 그려지기 때문이다. 가장 그럴듯하게 decision boundary를 그린 것이 위와 같은 형태일 것이다. 정말로 많은 split을 가지기 때문에 다소 복잡한 형태로 되어있는 것을 볼 수 있다. 가장 이상적인 결과는 우하향하는 직선이겠지만, 간단하게 답을 가지기 위해서 decision tree는 정말로 많은 branch를 가지고 있기 때문에 복잡하게 split되어 있을 수 밖에 없다.
Single attribute-based decision boundaries의 또 다른 limitation은 decision boundary가 수직으로 형성할 수 없다는 것이다. 아무래도 위와 같은 data distribution에서 가장 이상적인 decision boundary는 우하향하는 대각선으로 그려야할 것이다. 하지만 이는 현실적으로 불가능하기에 실제로는 이에 근사하는 계단 모양으로 여러 decision boundary가 합쳐진 상태로 만들 수 있다. 이러한 이유는 decision boundary가 각각의 axis에 수직으로 그려지기 때문이다. 가장 그럴듯하게 decision boundary를 그린 것이 위와 같은 형태일 것이다. 정말로 많은 split을 가지기 때문에 다소 복잡한 형태로 되어있는 것을 볼 수 있다. 가장 이상적인 결과는 우하향하는 직선이겠지만, 간단하게 답을 가지기 위해서 decision tree는 정말로 많은 branch를 가지고 있기 때문에 복잡하게 split되어 있을 수 밖에 없다.
