[데이터마이닝] Discriminative vs. Generative Learning

Bayes rule을 사용하는 statistical model인 Naive Bayes와 computer science인 neural network 각각을 알게 되었다면, 이번에는 이 둘이 사실상 같다는 사실을 알아보고자 한다. 이와 더불어 logistic regression과 Naive Bayes의 관계, discriminative learning과 generative learning의 관계에 대해서 알아보려고 한다. 특히 언제 어떠한 learning을 사용하는 것이 더 좋은지에 대해서 알아두면 좋다.

Logistic Regression

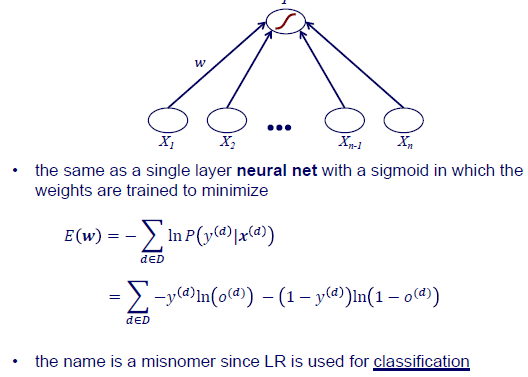Input과 weight를 곱해서 activation function을 통과하게 되는데, 이때 sigmoid function을 사용하게 된다. 이렇게 해서 prediction 결과를 얻게 되는데, 이러한 과정은 하나의 layer를 가지는 neural network와 동일하게 된다. 그리고는 학습을 위해서는 true와 prediction 사이의 error를 최소한으로 만들어야 된다. 그리고 error는 model parameter인 weight에 관한 식으로 구성되어져 있다. Binary classification task이기 때문에 error function이 cross entropy 식으로 되어 있다. 우리는 이 error function을 전체 training dataset에 대해서 최소로 만들어야 한다. 그리고 이것이 logistic regression의 목적이다.

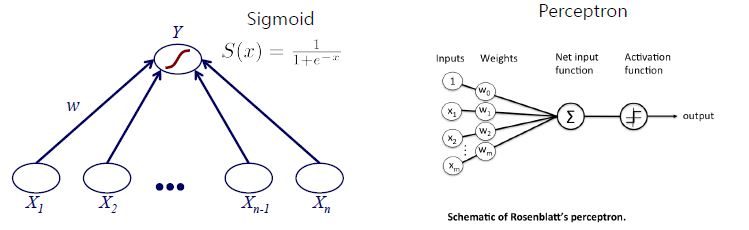Input data와 weight의 linear combination을 sigmoid function에 input으로 넣으면 다음과 같은 prediction 식이 완성될 것이다.

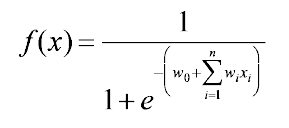Sigmoid function에서 bias term과 linear combination 식이 들어가있는 것을 볼 수 있다. 그리고 이러한 구조는 perceptron과 동일하게 볼 수 있다. 주목할 부분은 logistic regression에서 regression 부분이다. Regression이라고 하는 것은 사실 부정확한 명칭이다. 사실상 classification을 하는 것이지 regression을 한다고 볼 수 없다. 하지만 class label을 regression한다고 하면 그냥 classification과 동일하게 보면 된다. 그래서 결론적으로는 logistic regression은 classification을 한다고 보면 된다.

Naive Bayes

그렇다면 지금부터는 왜 logistic regression이 Naive Bayes와 동일한지 알아보려고 한다. 어떻게 보면 둘은 동일하지만 또 다르게 보면 둘은 다른 것으로 볼 수 있다.
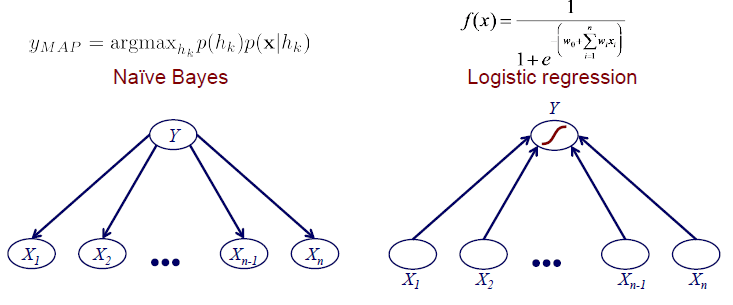Naive Bayes는 결국에는 MAP를 구하는 것으로, Bayes rule로부터 해당 식을 최대로 만드는 class label을 찾아야 한다. 해당 식은 prior $p(h_k)$와 likelihood $p(x|h_k)$의 곱으로 되어있다. 여기서 likelihood를 잘 보면 우리에게 $h_k$가 주어진 것이다. Likelihood는 결국에 우리에게 어떠한 class label이 주어졌을 때 해당 data가 얼마나 있는지를 나타낸다. 그리고 각 class label에 대한 likelihood를 비교해서 어느 class label일때 가장 확률이 높은지 판단할 수도 있다. Naive Bayes는 결국 이 중에서 가장 큰 class label을 고르자는 것이다. 그리고 이는 단순히 frequency를 counting하기 때문에 쉽게 구할 수 있을 것이다. 그래서 Naive Bayes를 graphical illustration을 통해서 살펴보면 좌측과 같이 class label이 주어졌을 때 input에 대한 확률이 어떠한지를 구하는 것이다.

하지만 logistic regression은 그 방향이 반대이다. Data가 우리에게 주어지고 transformation과 activation function을 통해서 prediction을 구하게 된다. Graphical illustrion을 보면 Naive Bayes와 logistic regression은 상당히 유사한 것을 알 수 있다. 하지만 이 둘을 비교했을 때 몇가지 차이점들이 존재한다. 우선 화살표의 방향이 반대이다. Naive Bayes는 class label이 주어지면 conditional joint probability를 구해야 한다. 그러나 logistic regression은 input이 주어지면 likelihood를 계산해서 prediction을 구하는 구조이다. Naive Bayes가 joint probability를 이용해서 한번에 구하는 구조이면, logistic regression은 data 하나씩 해서 prediction을 구하는 구조이다. 그리고 Naive Bayes는 자연스럽게 probability를 구하게 되지만, logistic regression은 sigmoid function을 통해서 0에서 1사이로 만들어주게 된다.

이제부터는 실제로 Naive Bayes가 어떻게 되는지 알아볼 것이고, binary classificatino task에 대해서 Naive Bayes를 사용한다고 가정해 볼 것이다.

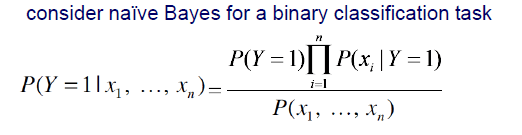
위와 같이 posterior가 있다면, 이는 Bayes rule에 의해서 정리할 수 있다. 그리고 분모의 $P(x_1,\dots,x_n)$을 우리는 evidence라고 부르게 된다. 아무래도 이 부분은 $Y$와는 직접적인 연관성이 존재하지 않는다. 그래서 우리는 사실상 이 부분을 무시하고 진행해도 상관이 없다.
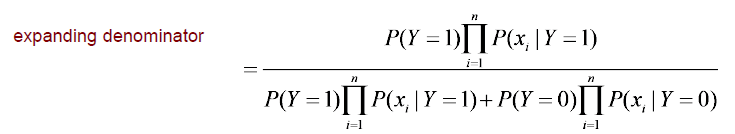하지만 이 부분을 무시하지 않고 분모 부분을 위와 같이 쪼개어 나타낼 수 있다. 이는 joint probability를 marginal probability와 conditional probability의 곱으로 나타낼 수 있다는 사실 때문에 가능한 것이다.

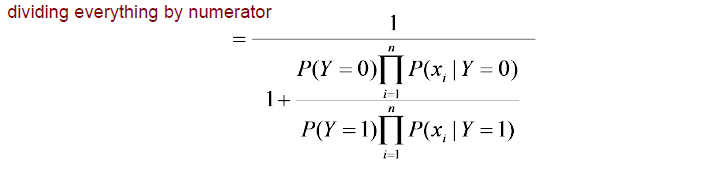그리고 여기서 분자와 분모를 분모의 첫번째 term으로 모두 나눠주면 된다. 그러면 그 결과와 위와 같을 것이다. 그러면 오로지 분모의 두번째 term만 식이 좀 복잡한 것을 볼 수 있다. 그러면 현재까지 posterior $P(Y=1|x_1,\dots,x_n)$ 식이 위와 같아진 것이다. 우리는 이 식과 함께 sigmoid 식을 유심히 볼 필요가 있다. 어느정도 전체적인 구조가 비슷해진 것을 알 수 있다. Sigmoid에 exponential이 존재한다면, 현재 우리의 식에는 분수 형태의 꼴이 존재하고 있다.

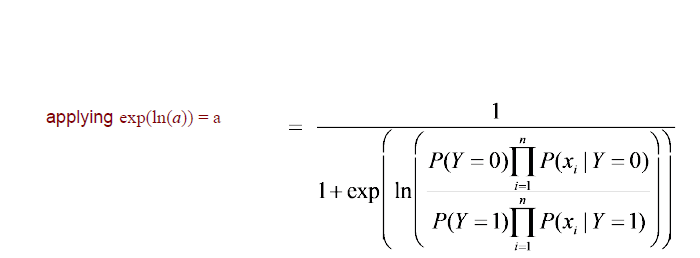여기서 우리는 간단한 trick을 이용해서 우리의 식을 sigmoid와 동일한 구조로 만들려고 한다. 그러기 위해서 exponential과 밑이 e인 log를 함께 사용해주면 된다. 그럼 다시 현재까지 상황에서 sigmoid 식과 비교해보면 유일한 차이점은 지수에 minus가 존재하지 않는다는 것이다.

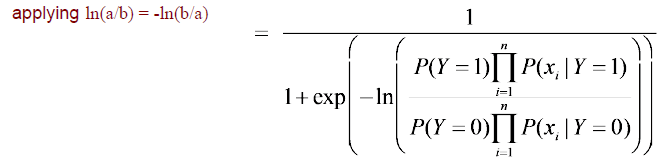그래서 log안에 있는 분자와 분모를 바꿔서 앞에 minus를 만들어 완전히 sigmoid function과 동일한 형태로 만들 수가 있다. 그러면 sigmoid function의 input이 현재 우리의 식에서 likelihood의 ratio에 log를 사용한 것과 같아지게 된다. 그럼 이제 Naive Bayes와 logistic regression 사이의 관계에 대해서 어느정도 알게 된 것이다. Logistic regression에서 $x$는 input data와 weight의 linear combination이었다. 반면, Naive Bayes에서 $x$는 likleihood의 ratio에 log를 사용한 것이다.

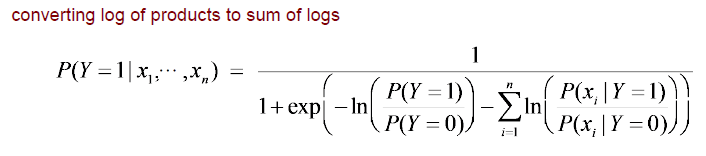그래서 이번에는 이러한 연관성을 좀 더 명확하게 만들어보려고 한다. 분자와 분모에 있는 식에 대해서 log의 성질을 이용하여 곱해져있는 것을 더해진 결과로 바꾸려고 한다. 기존의 식에 log와 product 식이 공존해있기 때문에 이를 log와 summation의 식으로 바꿀 수가 있다. 이러면 이제 확실히 기존에 logistic regression에서 sigmoid 식의 $x$에 들어가는 bias term $w_0$와 linear combination $\sum w_ix_i$가 더해진 형태와 완전히 동일해진 것을 확인할 수 있다.

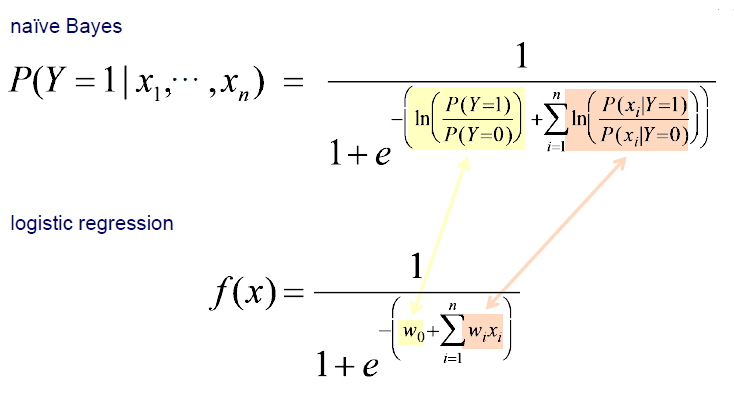이제 Naive Bayes 식인 posterior probability는 sigmoid의 형태로 바꿀 수가 있다.

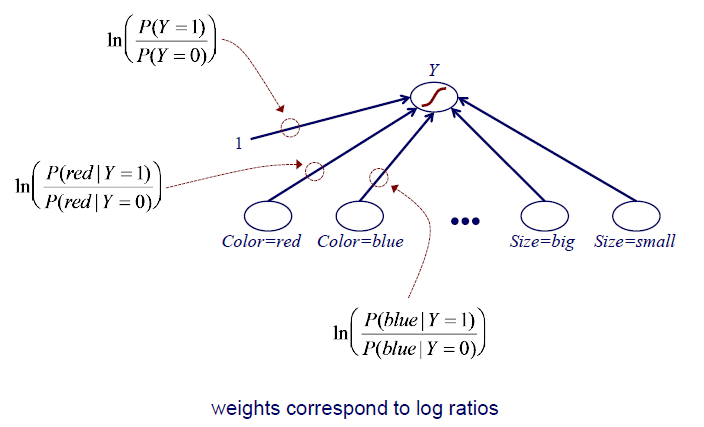여기서 가장 중요한 핵심은 Naive Bayes와 neural network가 동일한 graphical illustration을 나타내게 됨과 동시에 동일한 inductive bias를 가지게 된다. 여기서 inductive bias는 찾고자하는 model parameter를 이야기 한다. NN에서는 backpropagation을 이용하여 $w$를 학습하게 되고, Naive Bayes에서는 likelihood $P(X|h)$를 계산하게 된다. 여기서 우리는 동일한 model parameter를 찾으려고 한다는 것이다. Logistic regression은 weight를 찾기 위해서 backpropagation을 한다. 하지만 Naive Bayes에서는 단순하게 probability를 구하게 된다. 학습을 하기 보다는 그저 log ratio를 구하게 되면 이것이 바로 weight가 되는 것이다.

Naive Bayes와 logistic regression은 엄밀히 이야기하면 다른 것이다. 이들은 서로 다른 방식으로 model을 학습하게 된다. 그러나 이들의 hypothesis space bias는 동일하다.

그렇다면 이들은 동일한 model을 학습하는지 물어본다면 model 그 자체는 동일할 수 있어도 이들이 추정하는 parameter는 다르다고 이야기하면 된다. 이들은 model paramter를 추정하는데 있어 다른 방식을 사용하며, 여기서 Naive Bayes는 generative approach를 사용하는 반면 logistic regression은 discriminative approach를 사용하게 된다. Naive Bayes는 class label $h$를 data $x$로 이동하게 되지만, logistic regression은 반대로 $x$가 $h$로 이동하는 구조이다. 이렇게 input에서 output으로 가는 것을 discriminative function이라고 하는 것이고, 반대가 되면 generative function이라고 하는 것이다. 즉, learning에 있어 방향이 완전히 반대가 된다.

Generative vs. Discriminative Learning

Generative Approach

Generative approach에서 learning process는 class label probability $P(Y)$와 likelihood $P(X_1,\dots,X_n|Y)$를 추정하는 것이다. 그리고 classification에서는 $P(Y|X_1,\dots,X_n)$을 계산하기 위해서 Bayes' rule을 사용하곤 한다. 그래서 이를 구하기 위해서 먼저 likelihood를 정확하게 구할 필요가 있다.

Discriminative Approach

Discriminative approach에서 learning process는 $P(Y|X_1,\dots,X_n)$과 같이 input에서 output까지를 바로 구하게 된다.

Naive Bayes vs. Logistic Regression

• They have the same functional form, and thus have the same hypothesis space bias

• They use different methods to estimate the model parameters

Asymptotic Comparison

만약 모든 상황이 이상적이고 우리가 무한히 많은 양의 training instance를 가지고 있다고 가정했을 때 점근적으로 Naive Bayes와 logistic regression을 동일하게 볼 수 있다. Naive Bayes에서 conditional independence assumption들이 맞고 training instance들이 무한히 많다고 한다면 결국에는 Naive Bayes와 logistic regression은 동일한 classifier를 만들게 된다. 하지만 이는 매우 강력한 가정에 해당하게 된다. Naive Bayes에서 각 instance들이 모두 independent하다는 조건은 사실상 현실에서는 거의 불가능하기 때문이다. 간단한 예로 키와 몸무게만 보아도 서로 상관관계가 어느정도 존재하기 때문이다.

그래서 conditional independence assumption이 정확하지 않다고 한다면 logistic regression은 덜 biased 될 것이다. 그리고 학습된 weight는 부정확한 가정들을 보상할 수 있을 것이다. 예를 들어 우리가 두 개의 중복되지만 관련 있는 특징을 가지고 있는 경우를 생각해볼 수 있다. 따라서 logistic regression은 많은 training data가 주어졌을 때 Naive Bayes를 능가할 것으로 기대된다. 이는 conditional independence가 종종 정확하지 않을텐데 이때는 logistic regression이 더 나을 것이라는 이야기이다. 물론 항상 그렇다는 것은 아니다. Logistic regression이 Naive Bayes보다 나을 수 있다는 것은 model parameter를 올바르게 추정하기 위한 training data가 엄청 많을 때를 말한다.

Non-Asymptotic Analaysis

2001년도에 이 2가지 method에 대한 non-asympotitic analysis를 발표한 사람들이 있었다. Model이 정확하게 model parameter를 학습하기 위해서 혹은 convergence를 만족하기 위해서 Naive Bayes는 $O(\text{log}n)$만큼, logistic regression은 $O(n)$만큼 time complexity가 필요하다고 말했다. 여기서 $n$은 feature의 개수를 이야기한다. Naive Bayes가 logistic regression보다 더 효율적이라는 이야기다. 만약 sample의 개수가 많이 부족한 경우에는 Naive Bayes가 더 효과적일 것이다. 반면 sample의 개수가 충분히 많은 경우에는 logistic regression이 더 효과적이게 된다. 그 이유는 Naive Bayes가 적절히 훈련을 잘하려면 적은 양의 sample을 필요로하기 때문이다. 그래서 Naive Bayes가 더 빠르게 convergence를 만족하게 되고 training sample들이 적은 경우에는 Naive Bayes가 logistic regression보다 더 우수할 것이다. 다음은 간단한 data를 통해서 비교한 결과이다.

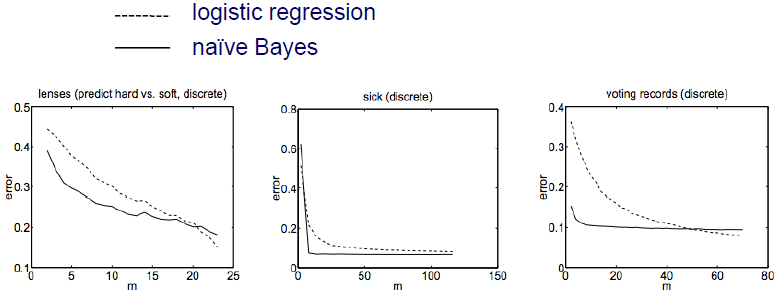
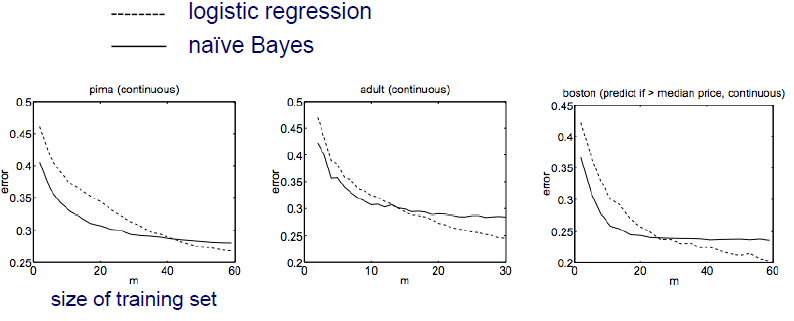위의 결과를 보면 training sample의 수가 적은 경우에는 Naive Bayes의 성능이 더 좋은 것을 볼 수 있다. Sample의 수가 많아지면 반대로 logistic regression의 성능이 더 좋아지게 된다.

Discussion

Naive Bayes와 logistic regression은 generative approach와 discriminative approach를 설명할 수 있는 가장 대표적인 예시 중 하나이다. 이들은 동일한 model을 서로 다른 방식으로 학습하게 된다. 만약 modeling assumption들이 유효하다면, 예를 들어 Naive Bayes에서 feature들의 conditional independence 같은 경우에, 둘 모두 동일한 model을 만들게 될 것이다. 하지만 이 가정들이 유효하지 않다면, 대부분의 경우에서 training set이 많은 경우에 일반적으로 discriminative approach가 generative approach보다 더 나은 성능을 보여주게 된다. 중요한 부분은 training data가 많은 경우에 한정된 것이다. 반대로 sample의 수가 적은 경우에는 generative approach가 더 나은 성능을 보일 가능성도 존재한다. 그 이유는 parameter들이 그들의 점근된 값들에 더 빠르게 convergence를 만족하기 때문이다. 그렇다면 여기서 우리는 어떻게 training data의 양이 많고 적은지를 이야기할 수 있을까? 사실 정해진 답은 없으며 실험이나 경험적으로 얻은 결과들일 뿐이다.