[데이터마이닝] Neural Network 3

지금까지 perceptron이 무엇인지 알아봤으며, perceptron을 쌓아서 multi-layer NN를 구성할 수 있었다. Hidden layer을 많이 쌓아 깊이가 더 깊어진다면 deep NN가 되는 것이다. 이를 학습시키는 것은 결국 weight를 update한다는 것과 동일하다. 그 방법으로 gradient descent를 사용하는 backpropagation을 알아보았다. 이제는 여기서 많은 질문을 할 수 있어야 한다.

Initializing Weights

첫번째 질문으로 weight를 어떻게 initialization을 해야하는지를 물어봐야 한다. 물론 임의로 initialization을 하면 될 것이다.
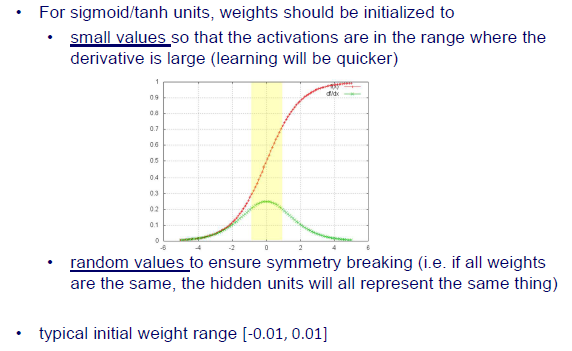만약 activation function으로 sigmoid나 tanh를 사용한다면 위의 graph에서 빨간 선과 같이 smooth하게 변화할 것이다. 즉, weight는 아주 작은 값으로 initialization 되어야만 한다. 물론 임의로 initialization되는 것이라고 해도 그 값은 작아야만 한다. 그 이유는 위에서 녹색 선을 보면 알 수가 있다. 위의 녹색 선은 빨간 선의 derivative이다. 여기서 볼 부분은 gradient 값이 큰 부분과 작은 부분들이다. Input 값의 절대값이 작을 때 gradient 값이 큰 것을 알 수 있다. 그렇기 때문에 weight 값이 작아야 gradient 값이 커져 어디로 가야하는지 알 수가 있다. 만약 weight 값이 작지 않다면 gradient 값이 작아서 어디로 가야하는지 알 수가 없어지게 된다. 우리는 이왕이면 gradient가 큰 값을 원하고, 이래야만 학습이 빠르게 진행될 것이다. Learning rate도 어디로 얼만큼 가야하는지에 중요한 역할을 하지만 이와 동시에 gradient의 크기도 함께 고려되어야한다.

그리고 weight는 symmetry breaking을 보장하는 random value들로 intialization 되어야 한다. 만약 모든 weight가 동일하다면, hidden unit들은 모두 같은 것을 설명할 것이다. 예를 들어 hidden unit이 2개 존재한다고 해보자. 그리고 여기에 관여하는 weight들이 서로 동일한 값을 가지고 있다고 해보자. Backpropagation을 통해서 model을 update한다고 했을 때, 각 unit이 동일한 값으로 update가 될 것이다. 만약 이렇게 update가 된다면, 2개의 hidden unit을 가지는 의미가 퇴색될 것이다. Hidden node를 사용한다는 것은 각각 다른 것들을 설명하고자 하기 위해서다. 그래서 일반적으로 initial weight는 -0.01에서 0.01 사이 임의의 값을 부여해서 사용한다.

Setting the Learning Rate

Learning rate는 어떻게 설정해줘야 하는 것일까? Initial weight는 작고 임의의 값으로 설정해주면 된다. 그래서 이번에는 learning rate는 어떻게 설정해줘야 하는지에 대해 알아보고자 한다.

Learning rate는 hyperparamete로, 사용하는 사람이 마음대로 설정해서 사용하면 된다. 하지만 문제는 적절하게 learning rate를 설정해줘야 convergence를 만족하게 된다. 여기서 적절한 learning rate는 heuristic으로 너무 크게 설정해도 model이 convergence를 만족하지 않을 것이고, 너무 작게 설정해도 만족하지 않을 것이다. 그렇기 때문에 너무 크지도 너무 작지도 않은 적절한 learning rate를 설정해주는 것이 중요하다.

Initial weight $w_{ij}$가 있을 때 gradient $-\frac{\partial E}{\partial w_{ij}}$는 weight가 어느 방향으로 가야하는지 알려주고 있다. 만약 우리가 설정한 learning rate가 너무 작은 경우에는 위에서 보다시피 weight가 조금만 이동하게 될 것이다. 물론 error는 줄어들지만 convergence를 만족하지는 않을 것이다. 반대로 learning rate를 너무 크게 잡으면 convergence 지점을 넘어가게 될 수도 있다. 그리고 error가 오히려 더 커지는 현상도 발생할 수 있다. 이러한 경우에 다음 update 시에는 또 반대로 넘어가게 되어 zigzag 현상이 발생할 수 있다.

Learning Rate and Momentum

이러한 learning rate에서 발생하는 issue를 해결하기 위해서 momentum이라는 것을 사용하기 시작했다.
기존의 weight를 update할 때는 learning rate와 gradient만을 사용했다면 여기에 momentum term을 더해주기만하면 된다. Momentum $\alpha$와 이전 반복시에 weight를 update하기 위해 사용되었던 것을 다시 사용하고자 하는 것이다. 현재 단계에서 어떻게 update가 되든간에 이전 단계에서 가고자 했던 방향 정보를 다시 활용하겠다는 것이다.

그렇다면 왜 이러한 momentum term을 사용하는 것일까? 그 이유는 바로 이전 update와 마찬가지로 동일한 방향으로 weight를 이동시키기 위해서이다. 현재 단계에서 잘못된 방향을 선택했다고 하더라도 이전 단계에서 진행했던 방향 정보와 함께 고려하겠다는 의미이다. 일종의 벡터의 합이라고 생각하면 적절한 방향으로 합의를 볼 수가 있다. 이렇게 하면 local minima에 빠지는 문제를 해결할 수 있다. Momentum 없이 현재 gradient만 반영하면 local minima를 피할 수 없지만 2가지 상황을 종합적으로 고려하게 되면 어느정도 local minima를 피할 수 있게 된다. Momentum을 사용하는 또 다른 이유는 flat region에서 step size를 증가시킬 수 있다. Error function에 만약 flat region이 있다면 gradient 값이 존재하지 않게 되어 어디로 가야할지 모르는 문제가 발생하게 된다. Saddle point 같은 지점이 바로 이 지점이다. 그래서 이전 상황까지 고려하게 된다면 saddle point라고 하더라도 계속 나아갈 수 있는 것이다. 이는 convergence를 만족시키는데 더 속도를 올려주는 효과를 보여주기도 한다.

Overfitting

지금부터는 NN에서 발생하는 issue들을 살펴보려고 하고, 가장 대표적인 예시로 overfitting에 대해서 알아보자. Decision tree에서도 만약 tree가 너무 복잡한 경우에는 overfitting이 발생했다. Overfitting의 문제는 performance를 향상시켜 주지만 그 값은 너무 작고 특히 training set에서만 적용된다는 것이다. Overfitted model을 test set에 사용하면 성능이 안나올 것이다. 그래서 model이 generalization 문제를 마주하게 된다.
예를 들어 model $h$에 대해서 error가 존재한다고 해보자. 우리는 training data에 대한 error와 data 전체에 대한 error를 구분하고자 한다. 그리고 model $h$와 model $h'$이 있다고 해보자. 두 model 모두 동일한 것을 prediction한다고 해보자. 이때 두 model을 training data를 통해서 error를 구한다고 했을 때 overfitting 된 $h$는 error가 상대적으로 더 작을 것이다. 반면, 전체 data를 사용한다고 하면 이야기는 달라질 것이다. 여기에는 training data 외에도 test data도 함께 포함되어 있다. Test data에 대해서는 $h'$이 더 작은 error를 보여줌으로써 더 나은 결과를 보여줄 것이다. 우리는 이러한 상황을 보고 model $h$가 overfitting 되었다고 이야기하는 것이다.

Network가 shallow한 경우에는 사실 overfitting이 그리 중요한 issue가 아니다. NN가 deep해지고 hidden node를 많이 가지게 되면 그만큼 많은 parameter를 필요로하게 될 것이다. 그러면 이 경우에는 overfitting이 중요한 issue가 될 것이다.
Overfitting의 한 경우를 보도록 하자. 2개의 feature와 3개의 class가 있다고 해보자. Class 1과 class 3에는 overlapping region이 존재하고 있다. Model이 조금만 복잡해진다고 하면 위와 같이 non-linear하게 학습을 할 것이고, 그렇게 되면 아주 적은 오차도 허용하지 않을 것이다. 이렇게 되면 새로운 data가 등장하게 되면 문제점이 생긴다. 현재 형성된 복잡한 decision boundary는 training data에 존재하는 일부 noise 때문에 생긴 것이다.

Regularization

그렇다면 NN에서 overfitting을 어떻게 해야 피할 수 있을까? Regularization이라고 부르는 방법들을 통해서 overfitting 문제를 해결할 수 있다. Decision tree에서는 early stopping이나 pruning 등을 통해서 overfitting을 피했다. NN에서도 regularization을 error에 적용함으로써 overfitting을 피할 수 있다.

Regularization은 training data를 완전히 fitting하는 것에서 벗어나 학습 과정을 biasing 시킴으로써 overfitting을 피하기 위한 방식을 말한다. 여기서 핵심은 완전히 training data에 fitting하는 것을 피하자는 것이다. Decision boundary를 살짝 느슨하고 간단하게 만들기를 원하는 것이다.

NN에서 사용할 수 있는 regularization method들이 다수 존재한다. Decision tree처럼 early stopping을 할 수도 있다. 학습을 하다가 data에 overfitting 되는 것이 보이면 멈추는 것이다. NN에는 이외에도 dropout, L1 / L2 penalty term 등의 기법들이 존재하고, 기존의 data 외에도 training data를 확장시켜서 overfitting을 피할 수도 있다. 우리는 이를 data augmentation이라고 한다.

Stopping Criteria

기존의 gradient descent를 이용해서 model을 학습할 때는 local minimum에 도달할 때까지 무수히 많은 반복을 통해서 학습을 진행했다.
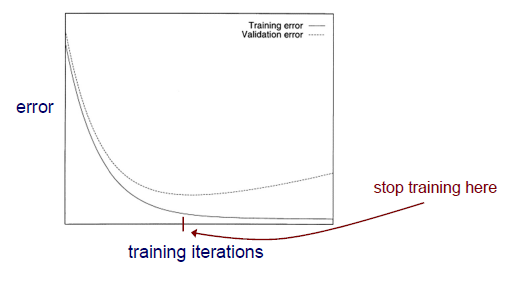학습이 진행되는 동안 위와 같은 error function 혹은 loss function이 감소할 것이다. 그리고 그 변화가 멈추게 되면 보통 학습을 중단하게 된다. 기존의 gradient descent를 사용하면 error가 더이상 낮아지지 않을 때까지 학습이 진행될 것이다. 하지만 학습을 너무 오래하게 되면 training data에 overfitting이 발생해 새로운 data에는 효과를 보지 못할 수 있다. 그래서 우리는 조금 더 일찍 학습을 중단할 필요가 있는 것이다.

Training set을 validation set과 training set으로 나눈 뒤 학습을 한 결과가 위와 같다. 특정 지점부터 validation error가 다시 올라가는 것을 볼 수 있다. 반면, training error는 계속해서 내려가는 경향을 보이다가 변화가 크게 없어지고 있다. Overfitting을 피하기 위해서 우리는 validation error가 가장 낮은 지점에서 학습을 멈추고자 하는 것이다. 그리고 이때의 weight를 return해서 사용하면 model이 training data에 완전히 fitting되는 것을 피할 수 있게 되고, 이를 early stopping이라 부르게 되는 것이다.

Dropout

Dropout도 overfitting을 피할 수 있는 방법들 중 하나로, 몇몇 node에서는 update를 하지 않겠다는 것이다. 즉, 완전한 학습을 거부하는 dropout은 unit들의 일부분과 그들의 weight를 무작위로 없애게 된다.

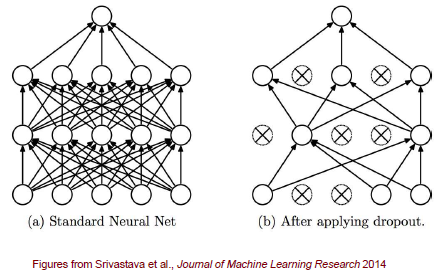좌측과 같이 FC layer로 구성된 NN가 있다고 해보자. 우리는 여기서 임의로 node를 몇개 골라서 dropout을 진행하면 이와 연결된 모든 connetction들이 끊기게 될 것이다. Dropout을 하게 되면 남아 있는 unit들을 이용해서 forward propagation과 back propagation을 수행하게 된다.

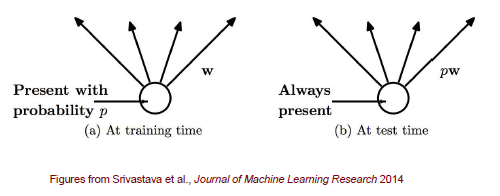앞서 training에서의 dropout을 보았다면, 이번에는 test에서의 dropout을 보려고 한다. Test를 할 때는 다시 모든 unit과 weight를 사용하게 되고, 이때 source unit이 drop out 되었을 확률에 따라 weight를 조정해서 사용하게 된다. 사실 dropout에도 여러 방법이 존재하지만, 가장 일반적으로는 확률 $p$에 따라 weight를 조정해서 사용하게 된다. 여기서 $p$는 해당 node가 dropout 될 확률을 이야기한다.

Encoding for NN

Input(Feature) Encoding for Neural Networks

지금까지 어떻게 overfitting을 피할 수 있는지 알아보았다. 이번에는 NN에서, 특히 DNN에서 많이 다루는 소재인 feature encoding에 대해서 이야기해보고자 한다. 우리가 NN를 다루고자 할 때 항상 input은 숫자 형식이어야 한다. 만약 input이 숫자가 아닌 nominal feature와 같이 다른 형식인 경우에 어떻게 해야할까?

Input feature가 nominal feature인 경우에는 어떻게든 숫자로 바꿔서 NN input으로 사용해야 한다. 우리는 이를 위해서 1-of-k encoding 혹은 one-hot vector를 사용해서 nominal feature를 숫자로 바꿔 사용할 것이다. One-hot vector는 하나를 제외하고 모두 0인 vector를 사용하겠다는 것이다. 위의 예시는 유전자를 one-hot vector로 바꿔서 표현한 것이다.

Ordinal feature는 nominal feature와 비슷하지만 순서가 존재한다. 그래서 thermometer encoding을 사용해서 위와 같이 1을 늘려가며 순서를 부여해서 사용하게 된다. 이렇게 하면 nominal feature나 ordinal feature에 대해서도 숫자로 encoding하여 input으로 사용할 수 있게 된다.

Real-valued feature는 individual input unit을 사용해서 나타낼 수 있으며, 여기서 중요한 것은 scale이 다른 경우에 대해서 먼저 standardization 혹은 normalization 등을 해줘야 한다는 것이다.

Output Encoding for Neural Networks

Input encoding에 대해서 알아보았다면, 이번에는 output encoding에 대해서 알아보려고 한다.
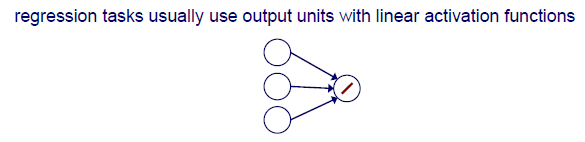Regression task에서는 일반적으로 linear activation function을 사용한다. 왜냐하면 regression task에서는 일반적으로 continuous value를 regression하기 때문이다. 우리는 output을 특정 범위로 제한시키고자 하는 것이 아니다.

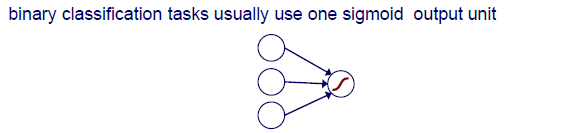Binary classification에서는 1, 0과 같이 2개의 상황을 분리해야 하기 때문에 sigmoid function같은 것을 사용한다.

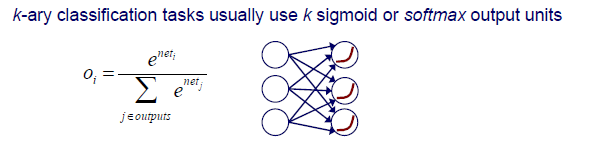k-ary classification은 k개의 output을 보여야하기 때문에 k개의 sigmoid function이나 softmax function을 사용하게 된다. Softmax는 activation function의 결과들을 이용해서 normalization 시켜 일종의 확률과 같이 output을 만드는 것이다.

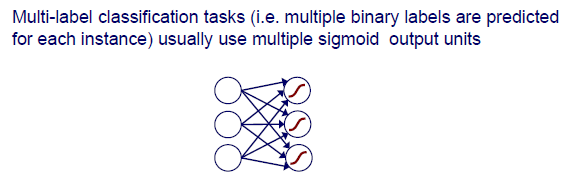Multi-label classification은 직전의 k-ary classification과는 약간 다르다. 여기서는 여러개의 binary label들이 각각의 instance에 대해 예측되는 것이다. 예를 들어 하나의 image라는 instance에 사람과 고양이가 있다고 했을 때, 우리는 이 image에 사람이 있다고 이야기 할 수도 있고 고양이가 있다고 이야기 할 수도 있다. 이때 여러개의 sigmoid function을 사용해서 각 function들로부터 사람인지 아닌지, 고양이인지 아닌지를 판단할 수 있는 것이다. 그저 해당 object가 존재하는지 아닌지를 판단하고자 하는 것이다.

Objective Function for Output Codings

이번에는 output encoding에서 objective function이라 불리는 error function들에 대해서 알아보고자 한다.

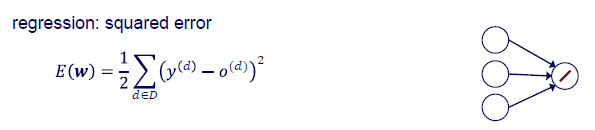Regression에서는 SSE를 사용한다.

Binary classification, multi-label classification에서는 cross entropy를 사용한다. Multi-label classification도 또한 binary classification이기 때문에 동일한 objective function을 사용하게 된다.

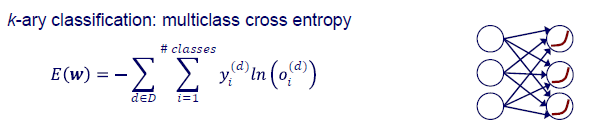k-ary classification에서는 multiclass cross entropy를 사용한다. 이는 여러 경우에 대해서 cross entropy를 구하는 것이다. Entropy 식을 보면 cross entropy의 경우에는 2가지 경우라 $p$와 $1-p$를 사용한 반면, multiclass cross entropy는 각각의 entropy를 구함으로 인해 좀 더 일반화 된 식이라고 생각할 수 있다.

Learning Representations

지금부터는 NN의 흥미로운 architecture를 알아볼 것이고, 이는 또한 더 나은 학습을 하는데 도움이 될 것이다. NN를 학습하는 것과 learning representation은 어떻게 연결이 되어 있을까?

Network가 학습을 통해서 무언가를 설명하려고 할 때 $w$라는 parameter를 학습하게 된다. $w$가 data $x$에 어떻게 작용하는지를 network를 통해서 알아내는 것이다. 이때 $w$와 $x$는 inner product를 통해서 서로 곱해지게 되고, 이는 projection으로 볼 수 있다. 그리고 projection이 하는 일은 transformation이다. 이는 다시 이야기하면 input data $x$가 있을 때 transformation을 통해서 $w^Tx$를 하면 어떻게 되는지 알아보겠다는 것이다. 그리고 여기에 weight $w$를 사용하는 것이다. 아무래도 학습을 통해서 최적의 $w$를 찾기 때문에 transformation의 결과는 좋아야 할 것이다. NN는 이러한 transformation을 알아내기 위해서 error를 최소한으로 줄이는 방향으로 학습을 한다.

Learning representation은 종종 학습 시스템이 얼마나 잘 작동하는지에 있어 가장 중요한 요소이다. Multi-layer NN의 매력적인 측면은 transformation을 사용하여 feature representation을 변경할 수 있다는 것이다. 우리는 hidden layer의 node를 input layer의 원래 feature로부터 변형된 새로운 feature라고 생각할 수 있다. Hidden layer가 많아지게 되면 더 많은 level의 feature들을 구성할 수 있다. 예를 들어, pixel로부터 edge, shape, face 등과 같이 hidden layer를 늘려감에 따라 더 고차원의 feature로 변형시킬 수 있다.

Competing Intuitions

NN를 통해서 이러한 representation을 학습하고자 할 때, 2가지 competing intuitions이 있다. 누구는 NN에 오직 2개의 layer(input + hidden + output)만 필요하다고 생각할 수 있고, 또 다른 누구는 network가 깊으면 깊을수록 좋다고 생각할 수도 있다.

Only need a 2-layer network

1989년에 등장한 reprsentation theorem은 sigmoid activation function을 사용하게 되면 하나의 hidden layer만으로 어떠한 continuous function을 설명할 수 있다고 말했다. 앞서 NN를 universal function approximator로서 설명했는데, 여기서 말하고자 하는 바는 하나의 hidden layer만 있어도 어떠한 function이든 설명이 가능하다는 것이다. Hidden node를 늘려감에 따라 어떠한 decision boundary도 만들 수 있다는 것이다.

실험을 통해서 hidden layer를 늘려가는 것은 accuracy를 향상하는데 도움이 되지 않으며, 이는 오히려 반대로 떨어뜨리는 것을 종종 볼 수 있었다. 그렇기 때문에 hidden layer의 수를 늘리는 것보다는 하나의 layer에서 hidden node의 수를 늘리는 것이 더 나은 결과를 보여준다고 여기서 말하고 있다. 그러나 이는 거짓임이 밝혀지게 되었다.

Deeper networks are better

실험을 통해서 성능을 평가했을 때 오히려 network가 깊어지는 것이 더 나은 결과를 보여주는 것이 밝혀졌다. 여기서 말하고자 하는 것은 하나의 hidden layer를 넓게 구성하기 보다는 차라리 여러 hidden layer를 통해서 network를 깊게 구성하는 것이 더 낫다고 이야기하는 것이다.

Hidden Units

그러면 hidden unit들이 실제로 하는 일은 무엇일까? Hidden unit은 transformation이 된 input을 학습하게 된다. Hidden unit은 input space를 perceptron만으로 충분한 새로운 space로 변화시킨다. 그리고 이들은 수치적으로 생성된 feature들을 나타낸다.
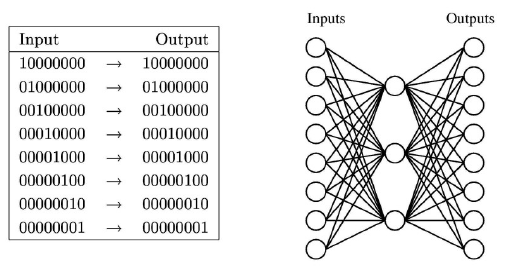Input과 output이 위와 같을 때 input과 output의 차이를 최소한으로 줄이고자 한다. 우리는 이러한 구조를 autoencoder라고 한다. 우리의 목적은 output이 input을 그대로 따라하고자 만드는 것이다. 이를 위해서 우측과 같은 network를 학습한다고 했을 때, hidden node들은 무엇을 학습하게 될까?

우선 위의 input과 output을 보게 되면 총 8자리로 구성된 것을 볼 수 있다. 이를 나타내기 위해서는 총 3개의 bit가 필요하게 된다. 그래서 이러한 구조의 network를 학습시키기 위해서, hidden unit들은 autoencoder 구조 상에서 compressed numerical coding을 학습하게 될 것이다. 다음은 학습 결과를 나타낸 것이다.

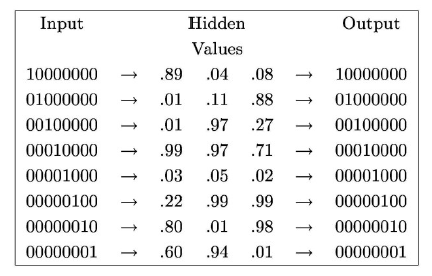첫번째 경우에는 상대적으로 큰 값과 작은 값 2개로 hidden value가 적혀있다. 아마 큰 값에는 1이 matching 될 것이고, 작은 값에는 0이 matching 될 것이다. 총 8개의 input을 3개의 hidden node들이 학습을 통해서 표현할 수 있어야 한다. 결국 hidden node는 input을 표현하기 위해서 compressed coding을 학습하는 것이다.

그렇다면 얼마나 많은 hidden unit이 필요할까? 초창기에는 data가 적기 때문에 parameter의 수가 적을수록 overfitting을 피할 가능성이 크기에 작은 network를 선호했었다. 하지만 최근에는 만약 early stopping을 사용한다면, 큰 network도 종종 hidden unit이 적은 것처럼 만들 수 있고, 더 나은 결과를 찾을 수 있다고 이야기하고 있다. Data가 충분한 경우에는 당연히 큰 network를 선호할 것이다.

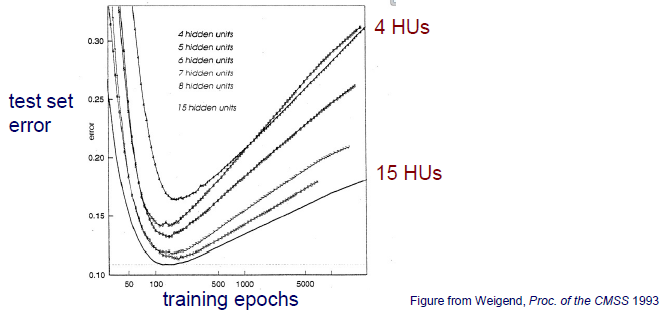위는 hidden unit의 개수에 따른 test set error를 보여주고 있다. 4개의 hidden unit을 사용하나 15개의 hidden unit을 사용하나 멈춰야 하는 지점이 비슷하다면 더 큰 model을 선호하게 될 것이다. 많은 수의 hidden unit을 포함시키는 것은 괜찮지만, 중요한 것은 어느 지점에서 멈춰야하는지를 알아서 멈춰줘야 그 효과가 드러나게 될 것이다.

Backpropagation with Multiple Hidden Layers

우리가 hidden layer가 여러개 있는 다소 큰 network를 학습시키고자 할 때, backpropagation을 사용할 것이다. 원칙적으로 backpropagation은 임의의 deep network를 훈련시키는 데 사용될 수 있다. 즉, 어떠한 network가 있든지 간에 backpropagation만 있으면 학습이 가능하다는 것이다. 하지만 이는 오직 이상적인 경우에 대해서다.

실제로 특히 sigmoid unit을 사용하게 되면 이는 제대로 동작하지 않을 수가 있다. 왜냐하면 gradient의 확산은 하위 layer에서 느린 학습으로 이어지기 때문이다. 만약 학습해야하는 layer가 많은 경우에는 error를 끝에서부터 하나씩 backpropagtion을 진행할텐데, input layer쪽으로 가면 갈수록 그 속도가 점점 느려지게 될 것이다.

이를 해결하기 위해서는 pretraining을 사용해서 network의 초반부 weight는 다른 network로부터 학습된 weight를 사용하면 된다. 아니면 rectified linear unit(ReLU)를 사용해서 backpropagation을 하면 된다. ReLU의 장점은 양수 범위에서 gradient가 1로 고정이 된다. 그래서 값이 작더라도 gradient 값을 고민할 필요가 없어지게 된다.

DN Approach 1 : Pretraining

Pretraining은 아마 greedy layer-wise training을 위한 unsupervised learning에서 사용할 수 있을 것이다. Unsupervised learning에서는 label에 접근하지 않는다. 그래서 그저 data $x$의 특징들을 알아서 학습하게 된다. Pretraining은 더 나은 parameter를 사용하기 위해서 network를 intialization하는데 도움이 된다.

또한 pretraining은 supervised learning에서도 사용이 될텐데, 일반적으로는 마지막 layer를 학습하기 위해서 사용한다. 혹은 종종 다른 layer들을 정비하기 위해서도 사용한다.

Autoencoder

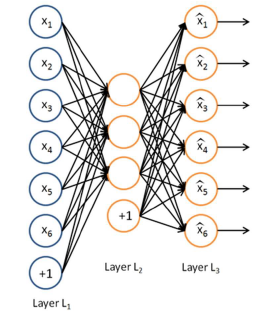Pretraining을 사용하는 대표적인 예시로 autoencoder가 있다. Autoencoder에서 hidden unit의 weight를 학습하는데 pretraining을 사용하고, 이것이 유용한 이유는 autoencoder가 input data $x$의 efficient representation을 학습하기 때문이다. Autoencoder에서 network는 input을 재구성하기 위해서 학습이 진행된다.

Autoencoder에는 변형된 형태들이 존재한다. Autoencoder의 목적은 원래 input과 재구성된 output의 차이를 줄이고자 하는 것이다. 그래서 이러한 autoencoder가 어떠한 경우에는 좋지만 또 다른 경우에는 좋지 않을 수가 있다. 그래서 때때로 상황에 맞게 autoencoder를 변형해서 사용하기도 한다.

• bottleneck : data compression을 목적으로 input보다 더 적은 hidden unit을 사용한다.
• sparsity : 대부분의 hidden unit을 0에 근사해서 활성화시키기 위해서 penalty function을 사용한다. 그래서 일부만 활성화해서 사용하는 것이다.
• denoising : 원래 input과 손상된 input을 예측하기 위해서 동시에 훈련시킨다.
• contractive : encoder가 작은 derivative 값을 가지도록 만든다.

여기서 핵심은 autoencoder를 weight를 pretraining 하는데 사용할 수 있다는 것이다. Autoencoder를 사용해서 pretraining이 된 weight는 성능을 보장하게 된다. 그래서 network를 intialization할 때 weight를 사용하고자 한다면 autoencoder를 이용하여 pretraining 시키는 것이 좋다.

Stacking Autoencoders

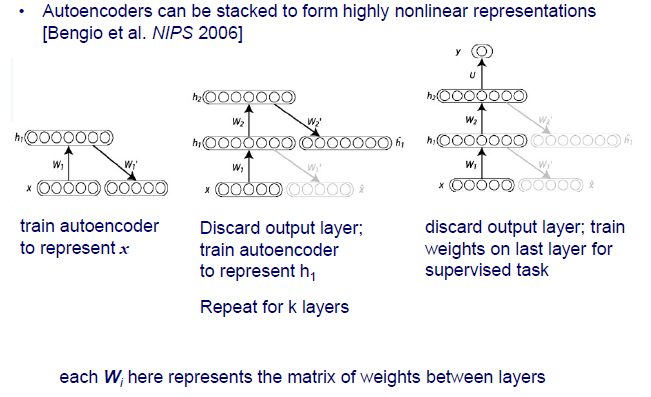그리고 이러한 autoencoder는 stack해서 사용할 수도 있다. 지금까지 hidden node들로 이루어진 하나의 layer에 대해서 알아보았다. 하지만 이를 여러겹으로 쌓아서 깊게 만들 수가 있다.

Fine Tuning

NN를 학습하고 난 뒤에는 fine tuning을 적용할 수 있다. 학습 완료 후, 전체 network에서 backpropagation을 실행하여 supervised task에 대한 weight를 fine tuning 할 수 있다. Autoencoder로 pretraining 시킨 weight $w$를 classification network에 initialization weight로 사용한다고 했을 때, 해당 network를 다시 학습하면서 이 weight를 조금씩 수정해나가는 것이다. 왜냐하면 backpropation이 적절한 weight로 시작하게 된다면 더 나은 성능을 보장하고 학습된 model은 임의로 initialization한 network보다 더 나은 결과를 만들어 낼 것이다.

DN Approach 2 : Direct Supervised Training

Multi-layer NN를 학습하는 더 좋은 방법 중 하나로 sigmoid 대신에 rectified linear unit을 사용하는 것이다. 이외에도 dropout을 사용하거나 architecture를 특별하게 만들게 되면 더 나은 학습이 가능해질 것이다.

Rectified Linear Units(ReLU)

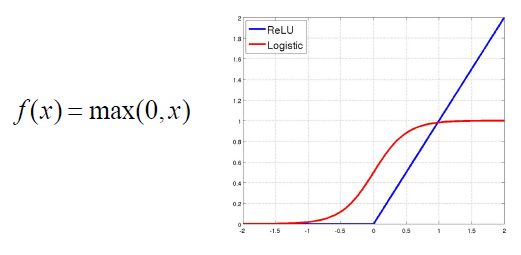Rectified linear unit은 위와 같이 생겼다. 0을 기준으로 양수 범위에서 gradient가 항상 1인 것이 특징이다. Sigmoid의 문제가 값이 커질수록 gradient가 0에 수렴한다는 것이다. 이러한 문제는 gradient vanishing 문제를 일으키게 되는데, ReLU를 사용하면 값이 커지더라도 gardient가 1이 되어 문제를 해결할 수 있게 된다.

Convolutional Neural Network(CNN)

또한 multi-layer NN를 잘 학습하기 위해서 특별한 architecture를 사용할 수 있다고 이야기 했었다. 가장 대표적인 예시로 convolutional neural network(CNN)을 이야기할 수 있다. CNN은 input이 spatial structure를 가지고 있는 task에 잘 동작하게 된다. Spatial structure를 가지는 input의 예시로는 image나 sequence 등이 존재한다.

CNN의 핵심 아이디어로는 local receptive field, weight sharing, pooling, 그리고 multiple layers of hidden unit이 있다. 이제부터 하나씩 자세하게 알아보도록 할 것이다.

위와 같이 instance가 $28\times 28$ pixel image로 되어있는 task가 있다고 해보자. 가로와 세로로 28개의 pixel들로 이루어진 image는 matrix로 생각해도 된다.

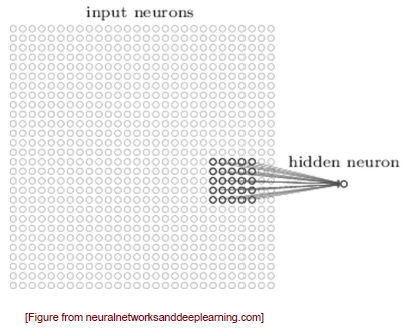각 pixel들이 hidden unit과 연결되어 있을 것인데, 만약 하나씩 전부 연결이 되어 있다면 resource를 낭비하게 되는 문제가 발생한다. 그렇기 때문에 CNN은 이렇게 hidden unit들과 전부 연결시키지 않는 방식을 택하고 있다. CNN은 image의 일부분만을 보는 방법을 사용해서 특정 부분인 receptive field만을 보게된다. 예를 들어 $5\times5$ patch를 사용하게 되면 그 부분의 특징을 파악할 수 있게 된다. 그래서 hidden neuron은 오로지 input node의 특정 부분만을 보게 되어 resource를 낭비하는 문제를 해결할 수 있게 된다.

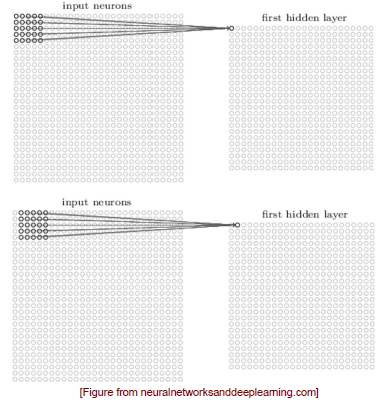Patch를 사용하게 되면 이를 이동시켜 나가면서 hidden layer의 neuron 하나씩 연결시키게 되는 구조이다. 이렇게 전체 input image를 보면서 hidden layer의 각 node에는 local receptive field에 대한 정보가 남게 되는 것이다. 여기서 중요한 것은 patch를 공유하게 된다는 것이고, 우리는 NN를 통해서 이 patch의 weight만을 학습하게 되는 것이다. 모든 unit들이 동일한 weight를 공유함으로써 unit들이 image 상에서 서로 다른 위치지만 동일한 feature들을 보게 되는 것이다.

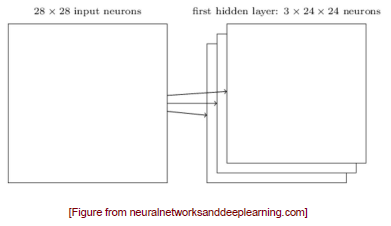동일한 feature들을 보게 되는 unit들의 집합을 feature map이라고 한다. Input image는 일반적으로 RGB의 3차원이기 때문에 한번의 convolution이 지나면 각 차원마다 feature map이 존재할 것이다. 그리고 차원이 줄어드는 이유는 convolution을 image내에서 바로 진행하기 때문이다.

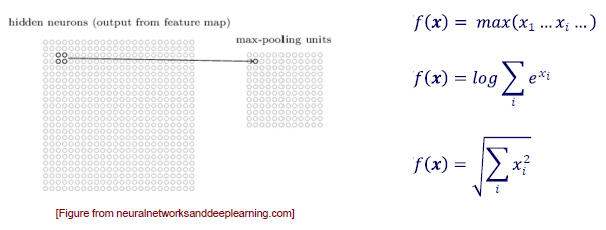Feature map을 얻은 후에는 pooling operation을 통해서 높은 차원을 낮은 차원으로 줄여주게 된다. 일반적으로는 downsampling을 통해서 pooling을 진행하게 되는데, 가장 대표적인 방식이 $2\times 2$ patch를 통해서 가장 큰 값만 남기는 방식을 택하게 된다. 아무래도 차원을 한번에 너무 줄이는 것도 문제가 되기 때문이다. 이외에도 mean pooling, average pooling 등 다양한 방법들이 존재한다. 여기서 핵심은 local region을 보면서 이러한 operation을 통해서 차원을 줄일 수 있다는 것이다. 그리고 이러한 operation들은 non-invertable하기 때문에 줄이는 쪽만 가능하다.

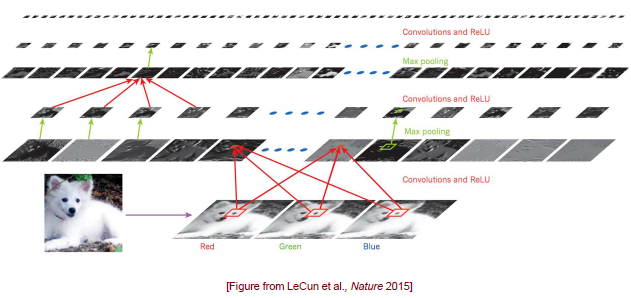위는 가장 전통적인 CNN 구조이다. Input image를 받으면 RGB 채널로 image를 분리한 뒤에 local receptive field를 볼 수 있도록 convolution operation을 하게 되고, 이후에는 ReLU를 통해서 activation 시킬 값만 남기게 된다. 이렇게 feature map이 만들어지게 되면 차원을 줄이기 위해서 max pooling을 사용하고 이 과정을 계속 반복해주면서 학습을 진행하게 된다. 이렇게 되면 전체적으로 피라미드 모양의 구조가 만들어지게 된다. 이 방법이 완벽하다고 이야기할 수 없지만 일반적으로 많이 사용됐던 구조이다. 사용자가 어떻게 network를 디자인하는지는 본인에 달려있기 때문에 어떻게 만들어도 상관이 없다.

Comments

Network를 깊게 쌓는 방식이 최근에 들어서는 여러 trick들과 함께 사용되면서 큰 성공을 가져왔다. Rectified linear unit(ReLU)같은 경우에는 gradient가 사라지는 문제를 해결해서 학습의 속도를 올릴 수 있었고, dropout을 사용해서 overfitting을 피할 수 있었다. 그리고 convolutional network와 같이 sparse하게 연결되는 구조를 사용함으로써 task마다 다른 bias를 통합할 수 있게 되었다. ImageNet과 같은 매우 큰 dataset과 GPU와 같은 hardware의 등장으로 더 나은 학습이 가능해졌다.

또한 stochastic gradient descent 방식을 사용함으로써 더 나은 학습이 가능해졌다. 이를 hidden unit이 없는 간단한 model을 통해서도 크기가 큰 dataset을 잘 학습할 수 있다. 그러나 종종 이 방법은 local minima에 빠지는 문제가 존재하기도 하지만, batch gradient descent와는 다르게 한번이나 혹은 적은 수로도 충분한 학습이 가능하다는 장점이 존재한다.

그리고 gradient descent와 backpropagation은 대부분의 상황에서도 일반화 된다는 장점이 있다. Output unit과 hidden unit이 몇개든, hidden unit의 layer가 몇개든, connetction pattern이 어떻든, 혹은 어떠한 activation function이나 objective function을 사용해도 잘 동작하게 된다. 하지만 이러한 상황에서도 data와 GPU가 충분하지 않으면 학습에 어려움이 존재할 것이다.