[데이터마이닝] Principal Component Analysis (PCA)

Principal component analysis(PCA)는 dimension reduction의 방법 중 하나로 매우 유명하다. 예를 들어 data의 dimension이 1000으로 매우 큰 경우에 dimension reduction을 통해서 2까지 줄이게 되면 우리는 visualization을 시킬 수 있게된다. PCA를 보기 전에 대표적인 dimension reduction으로 autoencoder를 생각할 수 있다. Autoencoder 구조상 높은 차원에서 낮은 차원으로 encoding을 하고 다시 높은 차원으로 decoding하게 된다. Autoencoder는 차원을 줄이고 늘릴 수 있는 encoder와 decoder를 학습하게 된다. 이러한 구조는 Fourier transformation과도 매우 유사하다. 원래의 space에서 frequency space로 보낸 뒤에 다시 원래의 space로 돌아오게 된다. Frequency space에서 특정 filtering을 하는 과정이 높은 차원에서 낮은 차원으로, 다시 높은 차원으로 보내는 과정과 동일한 셈이다. 결국 이러한 과정들이 dimension reduction을 필요로하는 여러 분야에서 볼 수 있는 것이다.

Principal Component Analysis (PCA)

d차원의 data point들이 주어지고 d가 매우 높은 차원인 경우에 우리가 원하는 것은 이들을 낮은 차원으로 projection시키는 것이다. 여기서 projection은 흔히 linear combination을 통해서 할 수 있다. 그리고 아무렇게나 낮은 차원으로 projection 시키는 것이 아닌 최대한 많은 정보를 보존시키는 space로 projection을 시켜야 한다. 가령 3차원에서 1차원으로 projection 혹은 transformation을 한다고 했을 때 최대한 많은 information을 보존시키고 싶은 것이다. 어느정도 information을 잃어버리는 것은 당연하다. 그래서 결국 information을 최대한 보존한다는 것은 information의 loss를 최소한으로 만들겠다는 것과 동일하다.

특히 원래의 data를 reconstruction할 때 squared error를 최소화하는 projection을 선택할 수 있다. 우리는 이러한 과정을 autoencoder에서 본 적이 있다. 하지만 그렇다고 autoencoder와 PCA가 동일한 것은 아니다. Autoencoder의 특징은 data로부터 encoding과 decoding을 학습하는 것이다. 하지만 PCA는 encoding과 decoding을 배우는 방식이 다르다.

Vision Application: Face Recognition

Dimension reduction의 대표적인 적용 사례 중 하나가 face recognition이다. 우리가 원하는 것은 facial image를 기반으로 특정 사람을 구분하는 것이다. 이를 위해서는 많은 image들을 서로 비교해야 한다. 여기서 핵심은 이 image들이 매우 고차원의 data라는 것이다. 일반적으로 $256\times 256$ pixel의 image들로 구성되어 있다. 물론 일반적인 image이긴 하지만 dimension의 관점에서는 매우 높은 것이다. 대략 65,000 pixel의 image들을 비교해야하는 것이고, 이때 facial hair, glasses, lighting 같은 것을 고려하게 될 것이다. 아무래도 모든 image들이 서로 다른 환경에서 얻은 data이기 때문에 비교를 하는 과정에서 작은 perturbation에 대해서도 robust하게 만들어야 한다. 여기서 특히 image끼리 비교하는 것은 좋은 방법이 아니다.

그래서 우리는 data의 dimension을 줄일 필요가 있다. 물론 65,000차원을 3, 6, 12와 같이 낮은 차원으로 dimension reduction을 하게 되면 information의 손실이 발생하게 될 것이다. 그래서 dimension reduction을 한다고 하면 최대한 의미있는 정보를 보존하기 위해서 원래의 data를 reconstruction해야 할 필요가 생긴다. 위의 예시와 같이 reconstruction한 결과들은 완전히 원래의 image와 동일하지는 않다. 하지만 여기서 그나마 차원이 높을수록 원래의 image와 점점 비슷해지는 것을 볼 수 있다. 그렇다면 여기서 의문인 부분은 어떻게 65,000차원에서 12차원으로 줄였음에도 불구하고 원래의 image와 상당히 유사한 결과를 만들어낸 것일까?

Matrix Decomposition

핵심은 basis와 관련이 있다. 예를 들어 총 36차원의 $6\times 6$ image가 있다고 해보자. 이 image를 나타내기 위해서 우리가 사용하는 basis는 vector가 아닌 one-hot encoded matrix이다. 36개 pixel 중에서 하나의 pixel만 1이고 나머지가 0인 matrix를 basis로 해서 총 36개를 사용하는 것이다. 그렇다면 이러한 basis가 좋은 basis일까? 물론 image를 정확하게 나타내기 위해서 사용되는 basis로 최고일 것이다. 그러나 이는 효율성의 측면에서 문제가 존재한다. 그래서 우리는 basis를 바꿀 필요가 있는 것이다. 기존의 basis를 제외하고 data를 projection 시키고 information loss를 최소한으로 만들 수 있는 새로운 basis를 찾아야 한다. 이것이 dimension reduction의 핵심이고, 그렇다면 어떻게 새로운 basis를 찾을 수 있는 것일까?

1. Eigendecomposition

이는 matrix decomposition을 통해서 할 수가 있다. 이중에서도 eigendecomposition에 대해서 알아보고자 한다. 먼저 square matrix $A\in\mathbb{R}^{n\times n}$가 주어지게 되면, 이 matrix는 eigenvalue와 eigenvector의 쌍인 $(\lambda, \chi)$으로 분해될 것이다. 그리고 이러한 과정을 우리는 diagonalization이라고도 부른다. 왜냐하면 다음과 같이 $A$가 3개의 matrix의 곱으로 표현되기 때문이다.

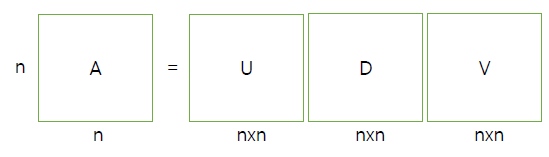$U$는 eigenvector $\chi$의 집합이고, $D$는 eigenvalue $\lambda$의 집합으로 diagonal matrix이다. 왜 이러한 과정이 중요한 것일까? 우리가 원래의 matrix $A$를 나타낸다고 했을 때, 기존에는 one-hot encoded matrix와 같은 basis를 사용해야만 했다. 하지만 eigendecomposition을 통해서 이제는 $u_1, \dots, u_n$까지 총 $n$개의 eigenvector를 basis로 사용할 수 있게 되었다. 결국 $u_iu_i^T$가 새로운 basis로서 $A$를 나타낼 수 있게 되었고, eigenvalue $\lambda_i$는 어느 지점에 대응되는지를 알려주는 coefficient와 같은 역할을 하게 되는 것이다. 결국 coefficient와 basis의 linear combination으로 동일한 $A$를 설명할 수 있게 된 것이다.

2. Singular-value Decomposition

또 다른 matrix decomposition의 방법으로는 singular-value decomposition(SVD)가 있다. SVD는 eigendecomposition과 다르게 주어진 matrix $A\in\mathbb{R}^{m\times n}$가 square matrix가 아니다. SVD도 마찬가지로 다음과 같이 $A$가 3개의 matrix 곱으로 표현될 수 있다.

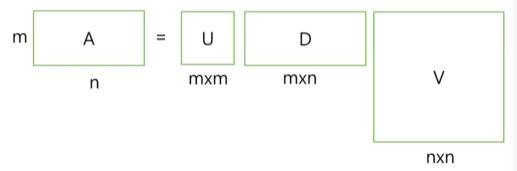$U$와 $V$는 singular vector, $D$는 singular value로 3개의 matrix의 곱을 통해서 $A$를 나타낼 수 있다. 자세하게 보면 $U\in\mathbb{R}^{m\times m}$는 unitary matrix로 $UU^{\ast}=I$를 만족하게 된다. $D\in\mathbb{R}^{m\times n}$는 retangular diagonal matrix로 non-negative real entry들로 구성되어 있다. 마지막으로 $V\in\mathbb{R}^{n \times n}$ 또한 uniatry matrix이다. 여기서도 핵심은 결국에 $A$를 coefficient와 basis의 linear combination으로 다시 나타낼 수 있다는 것이다.

Why do we care

그럼 이제 다시 PCA로 돌아가서 결국 우리가 원하는 것은 latent space이다. Latent space는 orthogonality에 관심을 가지는 어떠한 space여야 한다. 그래서 우리는 projection이 가능한 orthonormal basis가 있어야 한다. 그래서 지금부터는 orthonormal space를 가정해볼 것이다. 서로 orthonormal을 만족하는 basis $u_i$의 집합이 존재하는 것이다.

d차원의 data를 k차원의 latent space로 projection 시킬 수 있다고 해보자. 그러면 k차원 basis들이 $U$를 span하는 것이다. 이때 d차원의 $X$를 k차원으로 projection 시킨다고 하면 다음과 같이 표현할 수 있게 된다. Projection 결과 $k$개의 scalar value $\alpha$들을 coefficient로서 얻게 될 것이다.

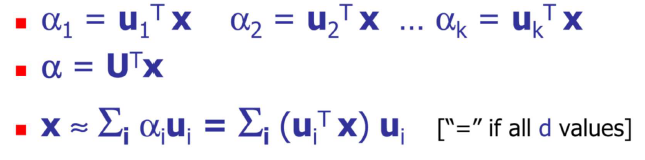NN에서는 $W^TX$에서 weight $W$를 학습하게 된다. 이와 마찬가지로 PCA에서는 $X$를 $u_1,\dots, u_k$로 projection 시키는 것이다. 그렇게 얻은 $\alpha_1,\dots, \alpha_k$는 k차원에서의 coordinate가 된다. 모든 $\alpha$를 matrix로 표현하게 되면 $U^TX$가 되는 것이고, 원래의 data $X$는 coefficient와 basis의 linear combination 형태가 되는 것이다. 여기서는 $\alpha$를 구하는 것이 encoding이고 다시 $X$를 표현하는 것이 decoding과 같은 셈이다.

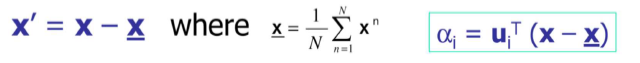이번에는 원래의 $X$를 사용하기 보다는 centered vector를 사용해보고자 한다. 그저 원래의 data에서 mean을 뺀 것이다. 이렇게 하면 basis의 원점이 data의 평균에 맞춰지게 될 것이다. 통계학에서 standardization 기법과 같은 것이다.

Highly Correlated Data

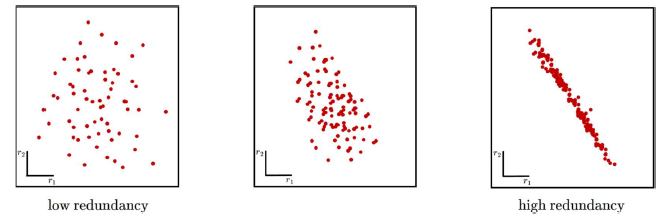우리는 dimension reduction을 원하고, 이것이 가능한 이유는 고차원에서 각 dimension이 서로 밀접하게 상관관계가 존재하기 때문이다. 밀접한 관련이 없다면 좌측과 같이 흩어져 있을 것이다. 하지만 관련이 있다면 특정 방향으로 data가 압축되어 분포할 것이다. PCA를 했을 때 우리가 원하는 것은 우측과 같이 data가 특정 방향으로 분포하는 상황 속에서 이를 나타낼 수 있는 새로운 axis를 찾는 것이다. 새로운 axis는 결국 data가 projection 되어도 information을 최소한으로 잃게 될 것이다.

Pricipal Component Analysis (PCA) (cont.)

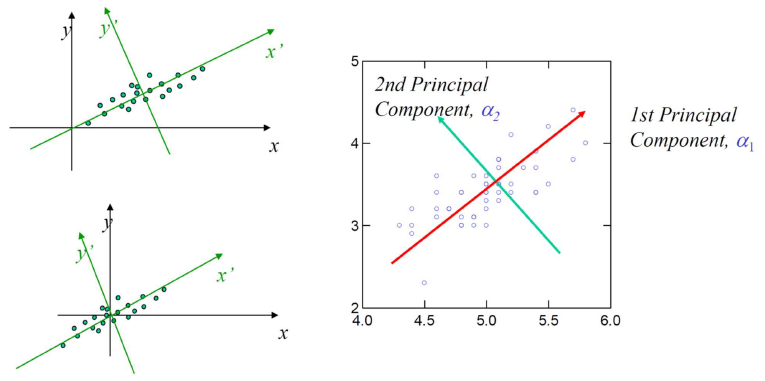PCA를 통해서 새로운 axis $x', y'$이 만들어졌을 때, 교차되는 원점이 data의 center와 일치하는 것을 볼 수 있다. 하지만 우리는 새로운 axis를 찾게 되었을 때도 해당 원점이 기존의 원점과 일치하기를 원한다. 그래서 우리는 data centering을 하는 것이고, 새로운 axis $x',y'$을 pricipal component(PC)라고 할 것이다. 우측과 같이 빨간선이 초록선보다 더 data의 경향을 따르고 있으므로 이를 1st pricipal component라고 하고 초록선을 2nd pricipal component라고 할 수 있다. Data의 경향에 따라 순서를 나누는 것 같지만 실제로는 information의 손실이 얼마나 적은지를 따졌을 때를 말하고 있는 것이다.

Minimize Reconstruction Error

우리는 새로운 axis $u_i$를 찾기 위해서 이들의 존재성에 대한 가정을 해야한다. 그래서 data를 N개의 D차원 vector $x=<x_1,\dots,x_d>$로 가정할 것이다. 우리는 D차원의 vector를 총 N개 가지고 있는 셈이다. Data $X$를 표현한다고 했을 때 row가 $n$개고, column이 $d$개인 것이다. 그렇다면 이제 이 $X$를 $u$의 관점에서 다시 표현하고자 한다.

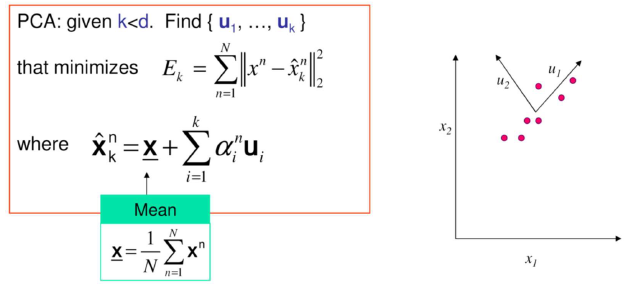PCA를 이용해서 dimension reduction을 한다고 했을 때, 우리는 orthonormal latent space를 찾고자 한다. 그래서 $u_i$와 $u_j$의 곱은 해당 axis가 동일한 경우에는 1이고 나머지는 0이 될 것이다. PCA는 원래의 d보다 작은 k가 주어졌을 때 $\{u_1,\dots, u_k\}$를 찾아야 하는 것이고, k가 d가 될 수도 있지만 이러한 상황은 원하지 않을 것이다. 그리고 이 vector들은 원래의 data와 새로 만들어진 data 사이의 error $E_k$를 최소한으로 만들어야 한다. Encoding과 decoding을 거쳐 생긴 $\hat{x}_k^n$은 data의 center로부터 새로운 axis와 coefficient의 linear combination한 결과만큼 이동한 data로 볼 수가 있다.

이전의 k가 d로 바뀌게 되면 완전히 reconstruction 된 data $x^n$이 만들어지게 된다. d개의 $u$를 사용한다는 것은 원래의 data와 동일한 차원의 basis를 사용한다는 것이고, 결국 information의 손실이 크게 나지 않는 원래의 data를 reconstruction하는 것과 같다.

$x^n$에서 $\hat{x}_k^n$을 뺀다는 것은 결국 $u_1$부터 $u_k$까지만 사용한다는 이야기와 같아진다. 그리고 $\alpha_i^n$을 원래의 data에 관하여 다시 정리할 수가 있다. 이렇게 만든 error $x^n - \hat{x}_k^n$은 모든 $N$개의 data에 대한 $E_k$로 정리할 수 있다. $i$와 $j$가 다른 경우에는 $u_i^Tu_j$가 0이 되기 때문에 제곱을 한다고 했을 때 고려되는 경우는 오로지 $i$와 $j$가 같은 상황일 것이다. Matrix 연산에서 제곱을 하게 되면 결국 앞의 항의 transpose가 적용되기 때문에 식을 정리할 수 있게 되고, 여기서 covariance marix의 정의에 따라 우리는 $E_k$를 최종적으로 나타낼 수 있게되는 것이다.

식이 어려워보이지만 여기서 중요한 부분은 $E_k$가 N개의 data에 관한 식이고, 마지막에는 covaraiance matrix로 정리할 수 있다는 사실이다. 그리고 이 error가 $u_{k+1}$부터 $u_d$까지의 remaining term들과 관련이 있다는 사실이다. 우리가 data를 나타내기 위해서 $u_1$부터 $u_k$까지를 사용한다고 했을 때, 나머지 부분이 error를 맡게되는 것이다.

정리해보면 $u$와 covariance matrix의 곱에 대해서 이 값을 최소한으로 만들어야 하는 것이다. Covariacne matrix는 data로부터 쉽게 구할 수 있어 주어지지만, $u$는 unknown 상태이다. 그리고 우리는 서로 orthonormal한 $u$를 찾아야만 한다.

그렇다면 이렇게 objective function과 constraint이 주어진 optimization problem을 어떻게 풀면 좋을까? 바로 Lagrangian multiplier를 이용해서 해당 식을 최소한으로 만드는 값을 찾으면 된다. Lagrangian multiplier의 역할은 objective function과 constraint를 하나의 식 $f(u)$로 합쳐주는 것이다. 이렇게 해도 원래의 식을 푸는 문제와 동일한 solution을 구할 수 있다.

그럼 이제 $f(u)$를 $u$에 대하여 derivative를 구해서 0으로 두면 critical point를 찾을 수가 있다. $\Sigma u$와 $\lambda u$가 같아지는 $u$를 찾으면 되는 것이다. 이 구조는 eigenvalue와 eigenvector 문제를 풀 때 보는 식과 동일하다. 어떤 matrix가 있을 때 eigenvector를 곱해주면 eigenvalue와 eigenvector의 곱과 같아지는 식이다. 여기서는 해당 matrix가 covariance matrix인 셈이다. 결국 우리는 covariance matrix의 eigenvector를 찾으면 되는 것이다. $d \times d$ covariance matrix를 eigendecomposition을 하게 되면 $(\lambda_i, u_i)$ pair를 총 d개 얻을 수 있을 것이다. 이렇게 얻은 $u$들이 PCA의 solution이 되는 것이다.

정리해서 살펴보면 $E_k$를 최소한으로 만들기 위한 solution으로 eigenvalue와 eigenvector와 관련된 식을 얻을 수 있었다. 이 식을 $E_k$ 식에 대입해서 정리할 수 있다. 그러면 $u_i^Tu_i$가 $\delta_{ii}$인데, $i$와 $j$가 같은 경우이기 때문에 1이 될 것이다. 그러면 최종적으로 $E_k$는 eigenvalue의 합이 된다. $E_k$를 최소한으로 만드는 것은 결국에는 가장 작은 eigenvalue를 사용하겠다는 것이다.

Summary

다음은 PCA의 summary이자 algorithm을 정리한 것이다.
우리는 $k$개의 eigenvalue와 eigenvector를 찾게 되고, 이는 pricipal component(PC)에 대응하게 된다. 먼저 data의 mean을 계산하게 되고, 이를 통해서 centered data를 구하게 된다. 그리고는 covariance matrix로부터 eigenvalue와 eigenvector를 구할 수 있다. 그리고는 eigenvalue를 크기 순으로 sorting 한 뒤에 가장 큰 것부터 $k$개의 pricipal component를 찾으면 된다. 따라서 eigenvalue의 값이 큰 순서대로 eigenvector를 선택하면 된다. 왜냐하면 eigenvalue가 error $E_k$를 구성하고 있고, 작은 eigenvalue에 대응되는 eigenvector들은 최소한의 information을 포함하기 때문에 이들은 버리고 값이 큰 eigenvalue에 대응되는 eigenvector를 선택하고자 하는 것이다.

PCA and SVD

우리는 지금까지 data $X\in \mathbb{R}^{N\times d}$를 centering을 한 후에 covariance matrix를 구해서 eigendecomposition을 하고 $k$개의 principal component를 택하는 과정으로 PCA를 할 수 있었다. 여기서 covariance matrix를 구하고 eigendecomposition을 하는 것이 다소 복잡해 보일 수 있다. 사실 크게 어렵지 않지만, 다소 어렵다고 느껴지는 경우에는 좀 더 간단하게 PC를 찾을 수 있는 방법이 존재한다. Covariance matrix를 구하지 않으며 eigendecomposition을 하지 않아도 된다.
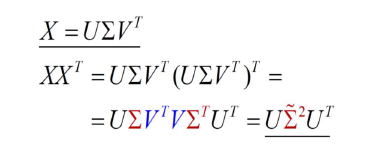바로 $X$로부터 바로 SVD를 하는 것이다. SVD를 바로 적용하게 되면 $U\Sigma V^T$로 $X$를 분해시킬 수 있다. 그래서 $XX^T$를 하게 되면 $V^TV$가 생기게 되는데 이는 서로 orthonormal matrix이기 때문에 계산하면 identity matrix $I$가 될 것이다. 그러면 $\Sigma \Sigma^T$가 남게 될 것이고, 결과적으로 $X$의 left singular vector들이 principal component가 될 것이다. Covariance matrix와 eigendecomposition 없이 그저 data에 SVD를 적용하기만 하면 principal component를 얻게되는 것이다.

PCA for Image Compression

그리고 autoencoder도 동일한 효과를 낼 수 있는데 굳이 PCA도 사용하는 이유가 무엇일까? PCA도 장점들이 존재하기 때문이다. Autoencoder에서 weight $w$와 PCA에서 pricipal component $u$를 비교해보았을 때 orthogonality를 만족하는 경우는 오로지 PCA뿐이다. 뿐만 아니라 autoencoder에서 $w$는 순서와 관련이 없지만, PCA에서 $u$는 순서와 관련이 있다. 우리는 covariance matrix의 eigenvalue를 통해서 principal component의 순서를 파악할 수 있다. 그리고 eigenvalue들은 원래의 data에 대해서 각 basis가 얼마나 많은 information을 포함하고 있는지를 알 수가 있다. 결국 PCA를 통해서 각 principal component의 정보량을 quantification 할 수 있다는 이점도 존재하는 것이다. Training과 optimization 관점에서 PCA는 그저 covariance matrix로부터 eigendecomposition을 하기 때문에 따로 진행하지 않는다. 이 말은 즉 학습이 필요한 autoencoder는 $w$를 구하기 위해서 그만큼 많은 양의 data가 필요하다는 것이다. PCA가 항상 autoencoder보다 뛰어나다는 것은 아니지만 이론적인 관점에서 많은 이점들을 가지고 있다.
PCA 적용 사례가 굉장히 많이 있다. 고차원의 data를 다루는 경우가 많을 것이고, 이를 저차원으로 보낼 수 있는 방법 중 하나가 PCA이기 때문이다. 적용 사례 중 하나인 image compression에 대해서 알아보고자 한다. 많은 facial image가 있다고 했을 때, 이들을 사용해서 covariance matrix를 구성할 수가 있다. 그리고 이로부터 eigenvector를 구할 수 있다. 만약 이 중에서 하나의 image를 택하고 eigenvector $u$를 이용해서 transformation을 한다면, 원래의 image를 재구성할 수 있을 것이다. 그렇게 위의 image들은 몇개의 principal component를 이용해서 image를 reconstruction 했는지에 대한 결과이다.

맨 눈으로 보기에는 64개부터 원래의 image와 유사한 것을 확인할 수 있다. 만약 원래 image가 $100 \times 100$ pixel로 되어 있다면, 우리는 10,000차원에서 약 100차원으로 basis를 바꿈으로 인하여 dimension을 크게 줄인 셈이 되는 것이다.

Eigenface

이러한 facial image는 Eigenface라는 연구 분야로 발전하게 되었다. Eigenface 분야도 마찬가지로 image가 얼굴인 data를 사용하고, 각 얼굴은 $256\times 256$ pixel로 되어 있다. 각 얼굴은 여러 column vector로 되어 있고, 이들은 하나로 concatenation해서 긴 vector 하나로 사용되었다. 이렇게 총 m개의 vector를 사용하여 matrix $A$를 만들게 되었다. 그래서 $A$는 facial image를 모아놓은 집합과 같고 각 column들이 하나의 facial image를 표현하게 된다.

이제 우리는 matrix $A$로부터 covariance matrix를 계산할 것이고, 이는 $AA^T$를 이용해서 구할 수 있다. 여기서 문제는 아무래도 covariance matrix가 매우 크다는 것이다. 물론 요즘같은 세상에는 이 정도의 크기로부터 eigendecomposition을 하는 것은 어렵지 않지만, 그 당시에는 해당 matrix의 크기가 너무나도 컸었다.

Computational Complexity

예를 들어 각 얼굴의 크기 $d$가 64k라고 했을 때, 총 500개의 얼굴이 있다고 가정해보자. Covariance matrix의 크기는 $d\times d$일 것이고, $d$개의 모든 eigenvalue와 eigenvector를 구하는데는 $O(d^3)$의 time complexity를 가질 것이다. 그리고 $k$개의 eigenvalue와 eigenvector를 구하는데는 $O(kd^2)$의 time complexity가 존재한다. 여전히 time complexity가 비효율적인 것을 볼 수 있다.

Clever Workaround

그렇다면 이러한 covariance matrix로부터 eigenvector를 구하는 효율적인 방법이 있을까? 매우 간단한 방법이 존재한다.
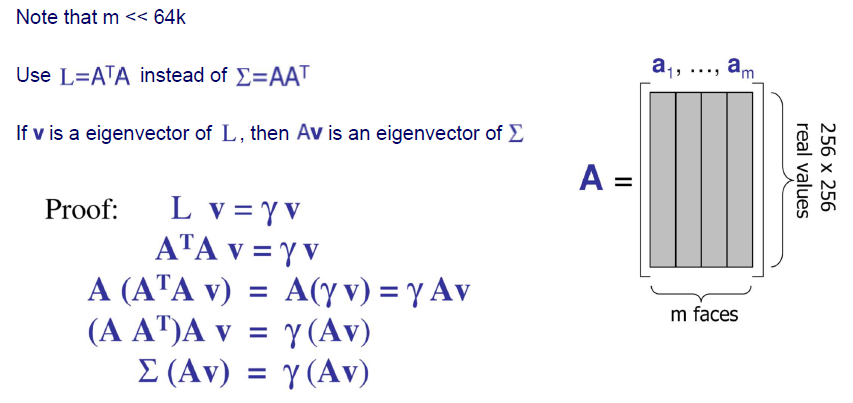다시 dimension이 64k이고 총 500개의 sample이 있다고 해보자. 여기서 생각해낸 방식은 기존의 covaraince matrix $\Sigma=AA^T$ 대신에 $L=A^TA$를 구하는 것이다. 그러면 $64k \times 64k$ 차원에서 $500 \times 500$ 차원으로 차원이 크게 줄어들게 될 것이다. 만약 $v$가 $L$의 eigenvector라면 $Lv=\lambda' v$를 만족하게 될 것이고, $Av$는 $\Sigma$의 eigenvector가 되어 $\Sigma (Av)=\lambda v$를 만족하게 될 것이다. 이는 위와 같이 간단한 proof로부터 증명할 수 있다. 이것이 말하는 것은 매우 expensive한 covariance matrix로부터 eigenvector를 구할 필요가 없다는 것이다. 훨씬 더 낮은 차원으로부터 eigenvector를 구할 수 있기 때문이다.

Dimensionality Reduction

다시 facial image로 돌아오면 좌측의 image로부터 각 feature의 수는 pixel의 수와 동일하다. 이제 covariance matrix를 구하고 eigenvector를 구하게 되면 원래 image dimension의 차원을 바꿀 수 있게 되고, 그로 인하여 우측의 image들이 eigenface가 되어 basis로 사용되는 것이다. 오직 20개의 eigenface를 통해서 모든 data를 표현할 수 있게 된 것이다.

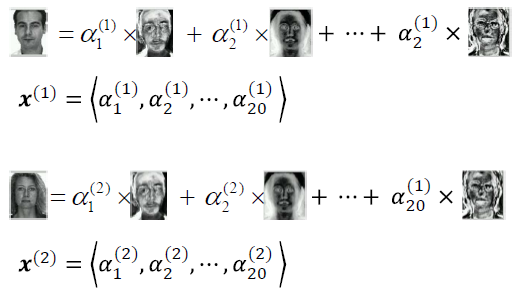Eigenface가 feature가 되어 coefficient와 linear combination을 통해서 image를 만들어내는 것이다.

Comments

PCA는 고차원에서의 data를 저차원의 subspace로 linear projection 시킴으로서 dimensionality reduction을 하게 된다. 그리고 이는 data에서 maximum variance 혹은 minimum reconstruction error를 수용하게 된다. 첫번째 principal component는 가능한 최대 variance를 가지고 두번째 principal component는 그 다음으로 큰 variance를 가지게 된다. 이러한 식으로 계속해서 순서를 가지게 되는 것이다. Principal component들은 covariance matrix의 eigenvector들이기 때문에 또한 orthogonal하다. PCA의 단점으로는 transformation을 거친 data가 원래 feature에서 semantics present를 잃기도 한다는 것이다. 왜냐하면 원래의 feature로부터 또 다른 dimension의 principal component를 찾았다고 했을 때 원래의 feature에 대한 정보와는 상관이 없어지게 된다.