[데이터마이닝] Neural Network 1

Neural network(NN) 혹은 artificial neural network(ANN)는 universal approximator로도 알려져있다. ANN은 거의 대부분의 function들을 approximation 시킬 수 있다. 이것이 ANN의 concept이고, 이를 수행하기 위해서 알아야하는 sub-concept들이 존재한다. 지금부터 하나씩 알아보고자 한다.

Neural Network

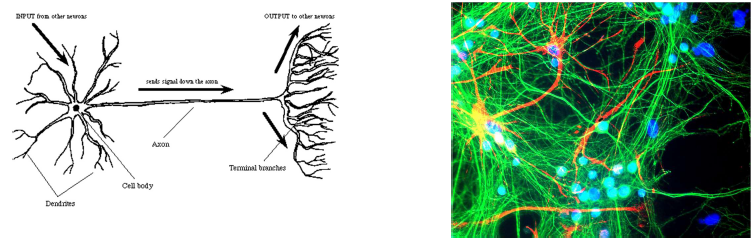NN이란 실제 neuron에서 영감을 받은 model이다. Neuron에서 dendrite들의 끝은 또 다른 neuron들과 연결되어져 있다. 그래서 여러 information들이 이 dendrite들을 통해서 전달될 수 있다. 그리고 여기서 information은 electrical stimulus를 기반으로 되어있다. 이 양이 충분해져서 중앙에 모이게 된다면 이 stimuls가 activation 상태가 될 것이고, 이로 인하여 axon을 통해 teminal branch들로 전달이 될 것이다. Teminal branch들은 또한 다른 neuron들과 연결되어 있어, signal이 또 다른 neuron까지 절달이 되는 것이다. 그래서 우리는 neuron을 simple information processing unit이라고 말할 수 있다. 이러한 과정을 ANN은 그대로 받아들이고 있다. 각 unit은 여러 real-valued input을 받아 single real-valued output을 내보내게 된다.

Perceptrons

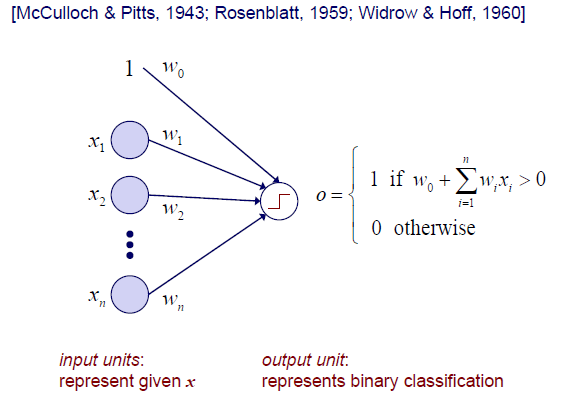이러한 neuron을 더 단순화시키게 되면, simple fundamental unit으로 만든 perceptron이 된다. 여러 input을 받아 하나의 output을 내놓는 구조를 perceptron이라고 생각하면 된다. Bias term과 여러 input이 동시에 들어와 중앙에 모이게 된다. 이들은 concatenation, summation 등의 어떠한 과정을 거쳐 information이 하나로 모인 뒤에 하나의 output으로 그 결과를 내놓게 된다. 실제로는 이 과정에서 linear combination을 수행하게 된다. $w$와 $x$들이 서로 곱해지고 여기에 bias term까지 더해져 이 값이 0이라는 threshold보다 크면 1이라는 output을 내놓고 아니면 0을 내놓을 것이다. 보통 이러한 function을 step function이라 하고, 여기서 특정 decision을 하는 것이다. 일종의 classification을 하는 것과 같은 것이다. Input $x$를 받아 1과 0을 나누는 binary classfication 결과를 output으로 내놓게 된다.

Example

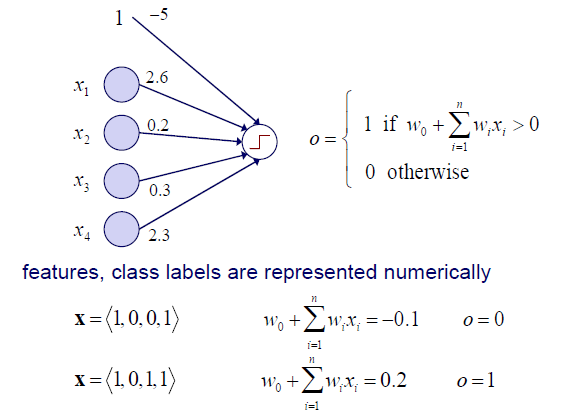위 예시에서 weight가 위와 같이 주어졌다고 해보자. Weight는 parameter로 고정된 값을 가지게 된다. Input으로 feature $x$를 받아 output으로 class label인 1과 0을 내놓게 된다. $x=<1,0,0,1>$이 들어오면 linear combination을 통해서 -0.1이라는 결과를 얻게 되고, 이는 음수에 해당하기 때문에 output으로 0을 내놓을 것이다. $x=<1,0,1,1>$이 들어오면 linear combination을 통해서 0.2라는 결과를 얻게 되고, 이는 양수에 해당하기 때문에 output으로 1을 내놓을 것이다. 결국 perceptron의 역할은 sample을 받아 decision을 하는 것과 같다.

Training a Perceptron

그렇다면 이런 perceptron을 어떻게 훈련시킬까? 앞서 $x$는 data로 이는 우리에게 주어진 것이지만, $w$는 model parameter로 우리가 훈련을 시켜 값을 tuning해줘야 하는 존재가 된다. Perceptron을 훈련시키는 방법은 먼저 임의로 weight들을 intialization하는 것이다. 그리고는 convergence를 만족할 때까지 training 과정을 반복해야 한다. Data와 weight를 통해서 먼저 특정 output을 계산할 수가 있다. 그리고는 각각의 weight를 update해주면 된다. Ground truth $y$와 prediction $o$와의 차이인 error를 줄여주는 방식으로 $w$를 업데이트 해야 한다. Error에 data sample과 learning rate를 함께 곱해줌으로써 얼마나 update를 해야하는지 그 양을 결정할 수 있다. 만약 ground truth와 prediction이 차이를 보이지 않으면 update를 멈출 것이다.

Representational Power fo Perceptrons

Perceptron은 실제로 binary classification을 하는 것과 동일하다. 지금부터는 어떻게 이러한 classifier가 feature space에서 설명되는지를 알아볼 것이다. Linear combination 결과에 따라 그 값이 양수면 1이고 음수면 0이었다. 여기서 linear combination 식을 다시 살펴보면 결국에 이 식은 2차원이라고 한다면 feature space에서 하나의 직선을 그리게 된다. 위와 같이 2개의 feature $x_1,x_2$가 있다고 했을 때, 2차원의 feature space 상에서 하나의 직선을 위와 같이 그릴 수 있다. 그리고 이 직선을 기준으로 1과 0을 나누게 된다. Sample이 들어오면 이 직선보다 위인지 아래인지를 계산해서 1이나 0을 부여하는 것이다. 그렇기 때문에 이 직선이 decision boundary가 되는 것이다.

여기서 bias term $w_0$가 만약 존재하지 않게 된다면, 항상 feature space의 원점을 지나는 직선을 그리게 될 것이다. 그렇게 되면 우리 model에 있어 flexibility를 크게 잃어버리게 되기 때문에 bias term은 중요한 존재로서 항상 필요한 것이 된다. 그리고 perceptron은 오로지 linearly seperable concept만을 설명할 수 있기 때문에 만약 sample들이 이 경우에 해당하지 않는다면 perceptron만으로는 data를 설명할 수 없게 될 것이다.

위 예시에서 feature space는 2차원이기 때문에 decision boundary가 하나의 직선이었다. 하지만 차원이 더 커지게 되면 decision boundary는 plane 혹은 hyperplane이 되어야 한다. 1차원에서는 decision boundary가 dot이 되고, 2차원에서는 line이 된다. 3차원에서는 decision boundary가 plane이 되고, 더 고차원에서는 hyperplane이 될 것이다.

Linearly Seperable Functions

앞서 perceptron이 linearly sperable concept을 설명한다고 했는데, 그렇다면 여기서 linearly seperable하다는 것은 무엇을 이야기하는 것일까? Linearly seperable이라는 것은 기본적으로 하나의 직선을 그린다고 했을 때 feature space에서 서로 다른 class를 분류할 수 있음을 의미한다. 다음의 예시를 통해서 알아보도록 하자. 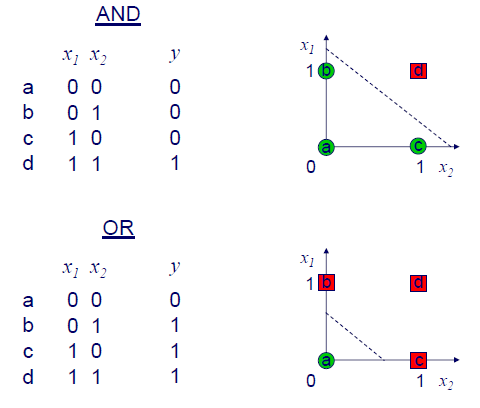먼저 AND의 경우에는 input이 모두 1인 경우에 output이 1이 된다. 0이 포함되면 AND operation의 output은 반드시 0이 된다. 이 결과를 우측의 feature space에 나타낼 수 있고, 하나의 직선을 어떻게든 그려서 그 결과를 나눌 수가 있다. 마찬가지로 OR operation도 하나의 직선을 통해서 그 결과를 나눌 수가 있다.

Is XOR Linearly Seperable?

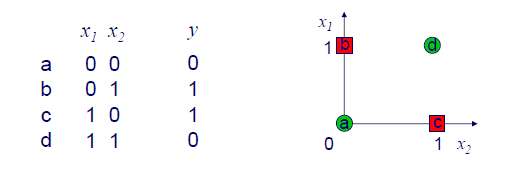
그렇다면 XOR의 경우는 어떨까? XOR operation은 input이 모두 같은 경우에는 0을 output으로 내놓게 된다. XOR의 경우 하나의 직선을 어떻게 그려도 그 결과를 완전하게 나눌 수가 없고, 이는 linearly seperable한 경우가 아니게 된다.

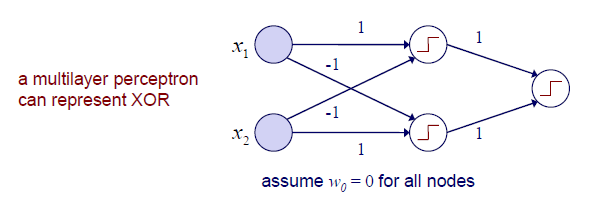이를 해결하기 위해서 ANN에서는 perceptron을 여러 layer를 이용해 쌓는 구조를 통해서 문제를 해결한다. 하나의 perceptron은 하나의 output을 내놓는데, 이를 여러 perceptron을 통해서 여러개의 output을 내놓은 뒤에 이를 다시 다음 perceptron의 input으로 사용하게 된다. 위의 예시는 총 3개의 perceptron을 사용한 것이고, 이렇게 perceptron을 여러개 쌓아서 XOR과 같은 non-linearly seperable한 경우를 해결할 수 있다. 그리고 perceptron을 여러개 여러층으로 쌓게 되면 이를 우리는 multi-layered perceptron이라 해서 MLP라고 부른다.

Multi-Layer Neural Network

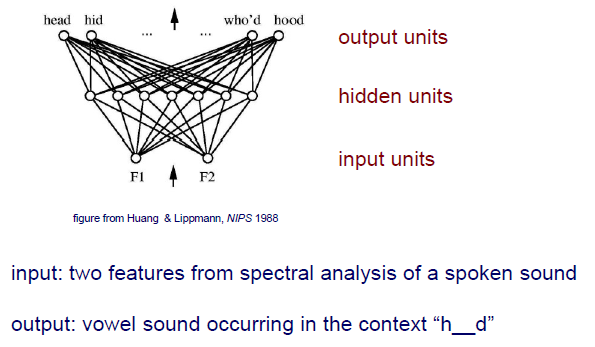MLP 구조를 살펴보면 input unit, hidden unit, output unit들로 구성되어 있다. 처음 MLP가 등장했을 때는 소리를 frequency domain으로 보내 얻은 2개의 band를 input feature로 사용했었다. 그리고 output은 서로 다른 h를 시작으로 d로 끝나는 소리들을 내놓았다. 이 문제는 사실 매우 어려운 문제이다. 오로지 2개의 feature만으로 10개의 소리를 구분해야 하는 것이었다.

Decision Regions of Multi-Layer NN

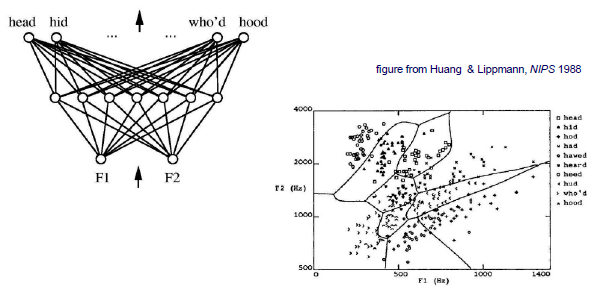좌측의 MLP가 실제로 수행한 결과과 우측에 보이는 figure이다. MLP는 하나의 직선만을 사용하는 구조가 아니다. 그렇기 때문에 우측과 같이 무수히 많은 decision boundary가 생기게 된 것이다. 우측의 결과는 사실 7차원의 hidden space에서 생긴 hyperplane들이다. 그리고 이를 다시 2차원에 projection하게 되면 곡선의 형태를 보이게 되는 것이다.

Learning in a Multi-Layer NN

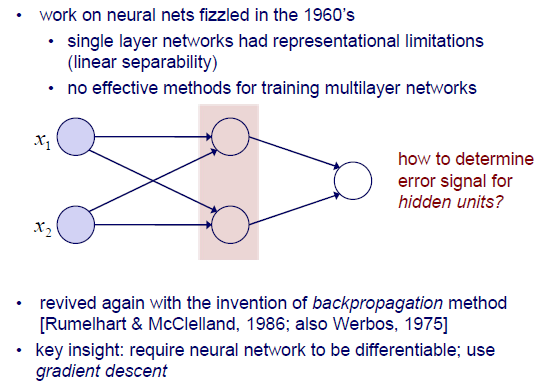Perceptron과 같이 하나의 layer를 가지는 network는 표현하는데 있어 한계점들이 존재했다. Perceptron은 매우 간단한 decision boundary 하나를 학습하게 된다. 그렇기 때문에 MLP가 등장한 것이고, 여기서 문제는 이 MLP를 학습할 효과적인 method들이 존재하지 않았다는 것이다. Perceptron에서는 error를 줄이고 weight를 update하는 식으로 학습을 진행했었는데, 이를 MLP로 확장시킬 방법이 존재하지 않았던 것이다.

그렇다면 hidden unit이 여러개가 되었을 때 error를 어떻게 결정해야하는 것일까? 1960년대 당시에는 아무도 그 해답을 발견하지 못했다. 그러다가 약 20년이 지난 후에야 backpropagation이라는 method의 등장으로 MLP를 학습할 수 있게 되었다. 여기서 핵심은 NN가 differentiable해야 한다는 것이다. 그래야 gradient descent를 이용해서 backpropagation을 수행할 수가 있게 된다. 여기서 network가 differentiable하다는 것은 weight와 activation function으로도 불리는 step function 모두에 해당하게 된다. 그리고 gradient descent를 구하는데 있어 gradient를 계산하기 위해서는 반드시 model이 differentiable해야 한다. 그렇다면 여기서 조금 전에 살펴본 step function의 경우에는 1과 0의 교차 지점에서 differentiable한 조건을 만족할 수 없게 된다. 그래서 그 당시에 step function에 문제가 있어 gradient descent를 사용할 수 없었다.

Gradient Descent in Weight Space

그렇게 시간이 흘러 backpropagation을 사용할 수 있게 되었고, 이에 따라 model이 differentiable 해야만 했었다. 기존의 step function이 문제를 일으켰기 때문에 대안으로 다른 function을 사용했고, 이로 인해 deep learning이 널리 사용되게 되었다. 해당 activation function들은 추후에 알아보도록 할 것이고, 우선은 gradient descent가 무엇인지 좀 더 자세하게 알아보고자 한다.
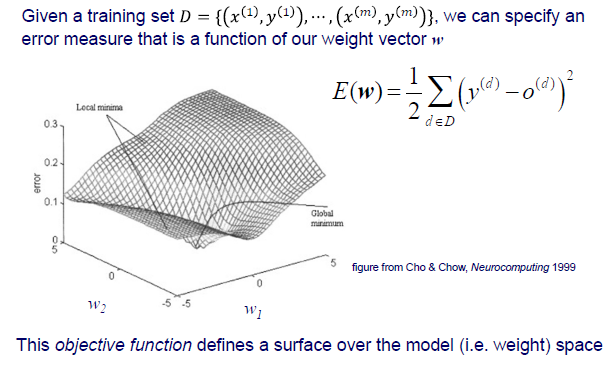우리는 weight space에서 gradient descent를 알아볼 것이고, 여기서 weight space는 data의 feature space와는 다른 space이다. Training set $D$가 label과 함께 주어졌을 때, 우리는 weight vector $w$의 function인 error function을 구체화 시킬 수 있다. Weight 값에 따라 우리는 특정 error 값을 가질 수 있고 이를 전체에 대해서 plot한 것이 위의 결과이다.

Weight마다 error function을 통해서 error 값을 squared summation을 통해서 얻을 수 있다. 즉, 우리는 weight마다 SSE를 얻게 될 것이고 global minimum 값이 어느 지점에선 존재하게 될 것이다. 우리는 error를 최소로 해야 하기 때문에 global minimum값을 찾아 해당 지점의 weight를 사용해야 한다. 물론 global minimum을 찾으면 좋겠지만 local minima들도 여러 존재할 수 있다. 결국 우리는 이러한 error function을 objective function이라고 부를 것이고, 이는 model의 weight space상에서 surface를 정의하게 된다.

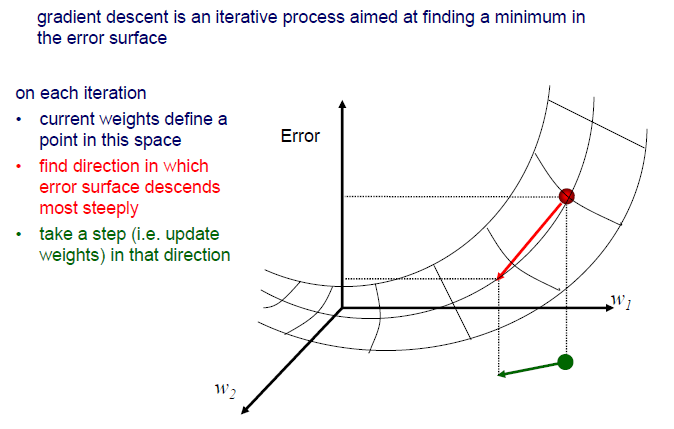결론부터 이야기하면 gradient descent를 통해서 error surface 상에서 minimum 값을 찾을 수가 있다. Weight space 상에서 error surface 위의 특정 지점에서 시작한다고 했을 때, 매 반복마다 error surface 상에서 값이 줄어드는 방향으로 weight를 update 해야한다. 현재의 weight를 space 상에서 하나의 점으로 생각할 수가 있고, 그 값이 점점 줄어드는 방향을 찾아 weight를 update하는 것이다. 감소하는 방향 중에서도 가장 많이 감소하는 방향을 찾는 것이 중요하다. Gradient는 현재 지점에서 어디로 가야하는지 알려주는 존재이다.

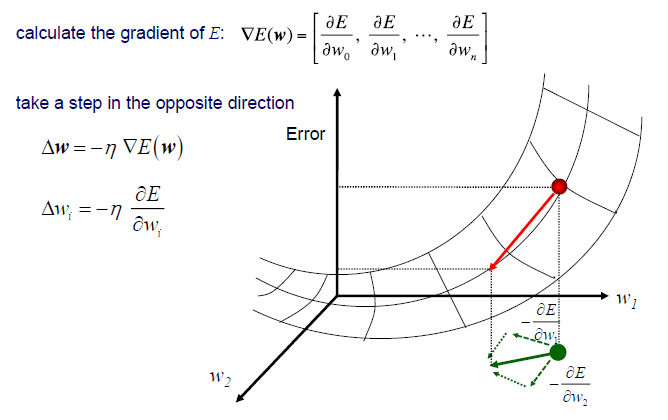2차원이라고 가정했을 때 실제로 수행해야 하는 것은 각 axis에 대해서 error $E$의 gradient를 계산하는 것이다. 그렇게 되면 각각의 partial derivative를 가지게 되고, 이는 error를 최소로 만들기 위해서 각 방향으로 어떻게 움직여야 하는지를 설명하게 된다. 보통 실제로 gradient를 구하게 되면 정반대의 방향을 가리키게 된다. 그래서 $\Delta w$에 -가 붙는 것이다. 그리그 해당 방향으로 얼만큼 이동할지를 learning rate로 결정하는 것이다. 결국 우리는 차원이 커져도 각각의 partial derivative만 구할 수 있으면 최적의 weight를 찾을 수가 있게 된다.

Sigmoid Function

앞서 perceptron에서 stpe function의 문제점이 differentiable하지 못하다는 것이었다. 그렇기에 parameter $w$에 대해 error $E$가 differentiable해지기 위해서는 network 또한 continuous function을 activation function으로 가져야만 한다. 그래서 기존의 discrete한 step function과 같은 역할을 하지만 continuous한 다음과 같은 function을 사용하고자 한다.
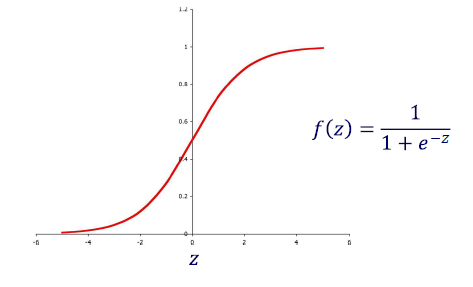우리는 hidden unit과 output unit에 기존의 threshold function 대신에 sigmoid function을 사용하고자 한다. Sigmoid function은 그 모양 자체가 smooth step function으로, 0이나 1에 근사하는 값을 가지게 되어 그 범위가 $-\infty \sim +\infty$까지로 어떠한 input이 들어와도 전체 domain을 0이나 1에 근사시킬 수가 있다.

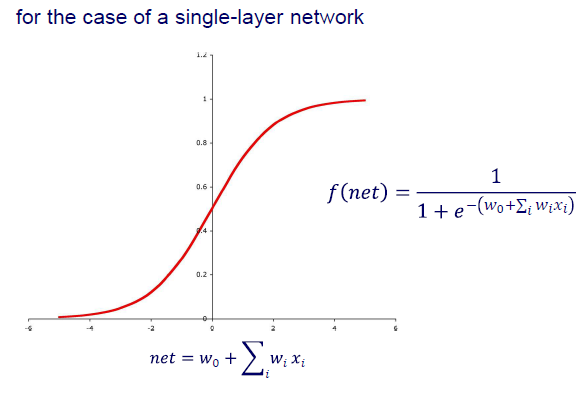Single layer network를 예시로 sigmoid function을 사용한다고 했을 때, 어떠한 input 값이 들어와도 우리는 이를 0과 1사이로 나타낼 수 있다. 여기서 일반적으로 0.5를 threshold로 설정하여 0.5 이상이면 1로, 0.5 이하면 0으로 classification 시킬 수 있다.

Batch NN training

지금까지 network를 통해서 하나의 output을 내놓는 것에 대해서 이야기했다. 이번에는 어떤 network와 m차원의 training set $D$가 주어졌을 때, 실제로 어떻게 학습이 되는지와 이를 통해서 어떻게 weight를 update하는지에 대해 알아보고자 한다.

가장 먼저 모든 weight $w$를 임의의 작은 숫자들로 initialization을 한다. 그리고는 optimal $w^\ast$를 찾기 위해서 gradient descent를 사용할 것이다. 그러기 위해서는 원하는 종료 조건까지 여러번의 반복 과정을 통해서 weight를 update할 것이다.

반복 과정에서는 먼저 error $E(w)$를 0으로 intialization 해야한다. 그리고 training set에 있는 각 sample들마다 network를 통해 output $o$를 계산하게 된다. 우리의 prediction과 ground truth를 이용해 error를 계산하게 되는데, prediction과 ground truth의 차이를 제곱한 뒤에 이전 error를 더해주는 식으로 error를 계산해준다. 이는 SSE를 이용한 것이고 다른 방법을 사용해도 된다. 그리고 이 SSE를 줄여야 하는데, 이는 gradient를 계산해주면 된다. Gradient를 통해서 어느 방향으로 가야 weight가 줄어드는지 찾게 되고, 이를 통해서 기존의 weight를 update 해주면 된다.

우리는 지금까지 training set에서 training sample들을 통해서 전체 error를 계산했다. 즉, 우리는 sample들의 batch를 통해서 error를 계산하고 update한 것이었다. 우리는 이를 batch training이라고 부른다. Sample들의 batch를 통해서 error를 minimization하는 식으로 weight를 update한 것이다.

Online vs. Batch Learning

그리고 이와는 반대되는 개념으로 online training도 존재한다. Online training은 training set의 sample들을 batch 사용했던 batch training과는 다르게 하나의 sample 혹은 small set을 이용해서 학습을 진행하는 방법이다.

Standard gradient descent인 batch training은 전체 training set을 이용해서 error gradient를 계산하는 방법이다. 100만, 1000만개의 sample들을 이용하는 경우가 바로 이 경우이다. 반면, stochastic gradient descent인 online training은 하나의 sample 혹은 mini-batch로도 불리는 small set을 이용해서 error gradient를 구하는 방법이다. 100만개처럼 많은 양의 sample들을 이용하는 것이 아닌 30개와 같이 적은 양의 sample들을 이용해서 gradient를 구할 수가 있다. 이 방법의 장점은 convergence를 만족하는데 훨씬 빠르며, local minima에 대해서 덜 민감하다. 아무래도 적은 양의 sample들만 보기 때문에 local minima에 아무래도 더 어려워지게 된다.

Online NN Training (Stochastic Gradient Descent)

오래 기다리기 힘든 경우 빠른 결과를 보고자 하는 사람들은 아무래도 stocahstic gradient descent를 더 선호할 것이다. Online training은 batch training과 대부분 비슷하게 진행이 된다. Batch training에서는 모든 sample들을 이용해서 error를 계산한 뒤 gradient를 구했다면, online training에서는 sample로 error를 계산하자마자 바로 gradient를 구하게 된다. 그리고나서 바로 weight를 update하는 것이다. 그렇기에 training set의 sample 개수만큼 update 과정이 일어나게 된다.

예를 들어 100만개의 sample이 있다고 해보자. 이전의 batch training에서는 1번의 update를 위해서 100만개의 sample을 모두 다뤄야 한다. 반면 online training의 경우에는 100만개의 sample만큼 100만번의 update를 하게 된다. 이 과정이 매우 빠르기는 하지만 그만큼 덜 안정적일 수도 있다. Robust하지는 않지만 사람들은 몇가지 trick들을 이용해서 online training을 사용하곤 한다. Deep learning에서는 online training이 어떻게 하면 더 안정적이게 만들 수 있을지가 하나의 issue가 된다.

Other Activation Functions

이번에는 또 다른 activation function들에 대해서 알아보고자 한다. 지금까지 step function과 sigmoid에 대해서 알아보았다. Sigmoid는 activation function 중 하나의 선택지에 속하게 된다.
사람들은 때로는 hyperbolic tangent function을 사용하기도 한다. Hyperbolic tangent function은 -1부터 1까지의 범위를 가지게 된다. 이외에도 rectified linear function인 ReLU function을 사용하기도 한다. ReLU는 step function이나 sigmoid function과 비슷하게 생겼는데 더 관심을 가지는 이유가 무엇일까? ReLU의 가장 큰 장점 중 하나는 gradient를 계산할 필요가 없다. Gradient를 계산하면 0보다 작은 경우에는 0이고 나머지는 1이기 때문이다. 즉, $x$가 양수인 경우에는 gradient가 항상 1이 된다. 물론 ReLU가 완벽한 activation function은 아닐지라도 매우 유명한 activation function임에는 틀림없다. ReLU는 data가 복잡하고 커질수록 더 유용하게 사용될 수 있다. 아무래도 복잡한 gradient일수록 time-consuming하기 때문이다.

Other Objective Functions

이번에는 또 다른 objective function들에 대해서 알아보고자 한다. 우리는 이전에 SSE에 대해서 알아보았다. 물론 SSE도 objective function들 중 하나의 선택지이다.
또 다른 objective function들로는 (binary) cross entropy나 multiclass cross entropy가 있다. 이 measure는 classification에서 error를 평가하는 방법들 사이에서 매우 유명하다.

Binary의 경우에는 $y$가 0 아니면 1이 될 것이다. Cross entropy 식을 보면 $y$가 0이 되면 앞의 term이 사라질 것이고 $y$가 1이 되면 뒤의 term이 사라질 것이다. 그리고 남아있는 term에서 실제로 계산되는 부분은 log뿐일 것이다. 만약 $y$가 1이라면, 우리의 prediction은 1에 가까워야 할 것이다.

Convergence of Gradient Descent

Gradient descent는 convergence를 만족할까? Gradient descent는 error function에서 minimum 지점을 찾아가기 때문에 convergence를 만족하게 될 것이다. 그리고 여기서 minimum은 multi-layer network에서는 local minimum이 될 것이다. 반면 single-layer network에서는 global minimum이 될 것이다. Multi-layer network의 경우 도달한 지점이 global minimum이 될 수도 있지만 local minimum이 될 수도 있다. 이 경우에는 항상 보장할 수는 없는 것이고, weight space 상에서 더 나은 solution이 존재할 수도 있다. 그리고 최근에는 local minima가 아마도 고차원에서 드물 것이라는 분석 결과가 있다. 우선 중요한 것은 multi-layer network에서는 global minimum을 보장할 순 없다는 것이다.