[데이터마이닝] Neural Network 2

Gradient descent는 model이 복잡해질수록 함께 복잡해지는 경향을 보인다. 하지만 activation function과 error function을 잘 선택한다면 이 과정이 간단해질 수 있다. 그래서 activation function과 error function의 최적의 조합을 찾는 것이 정말 중요하다.

Gradient Descent

이번에는 chain rule과 derivative 등을 기반으로 gradient descent를 어떻게 하는지 알아보고자 한다.

Simple Case 1

하나의 linear output unit을 가지고 hidden unit은 존재하지 않는 간단한 network를 예시로 생각해보자. 여기서 linear output이라는 것은 activation function이 linear하다는 것이다. Output $o$가 net과 동일한 이유는 linear function $y=x$의 형태로 net이 $w^Tx$와 같기 때문이다. 그래서 output $o$는 $w$와 $x$의 간단한 linear combination으로 식을 정리할 수 있다.

그리고 model의 prediction $o$가 정확한지 확인하기 위해서 SSE를 error function으로 사용하고자 한다. 여기서 summation은 전체 training set을 통해서 진행된다. Batch training에서는 전체 training set을 통해서 error를 계산하게 된다. 그리고 이 error를 $w$에 대해서 derivative를 구하게 된다. 반면 online training에서는 gradient를 각각의 sample에 대해서 구하게 된다. 그래서 batch training 식에 존재하던 summation이 online training에서는 보이지 않는 것이다. 식 내부에 $w$가 보이지 않는 것은 이미 $o$에 포함되어 있기 때문이다. 그래서 우리는 여기서 chain rule을 사용해서 gradient를 구해야 하는 것이다. Online training에서의 chain rule을 간단하게 살펴보도록 하자.

하나의 sample $d$에 대한 error를 $w$에 관한 gradient를 계산하고자 한다면 위와 같이 3개의 term으로 나눌 수가 있다. Error, $o$, net에 대한 function을 그저 원하는 것에 대해서 미분을 해주면 된다. Error는 $-\frac{1}{2}(y-o)^2$이고, $o$는 net이고, net은 여기서는 $w_0+\sum w_ix_i$가 된다. Derivative를 구한 뒤에는 모두 곱해주면 결과적으로 chain rule을 사용한 것이 된다.

Simple Case 2

이번에는 sigmoid output unit을 가지고 hidden unit이 없는 network를 보고자 한다. 여기서 objective function으로는 cross-entropy를 사용한다. 그리고 net은 이전 예시와 동일한 linear combination 식을 사용할 것이다. Sigmoid function에는 재미있는 성질이 존재한다. 바로 sigmoid function의 derivative를 구하게 되면 기존 sigmoid function과 관련된 식으로 나타낼 수가 있다.

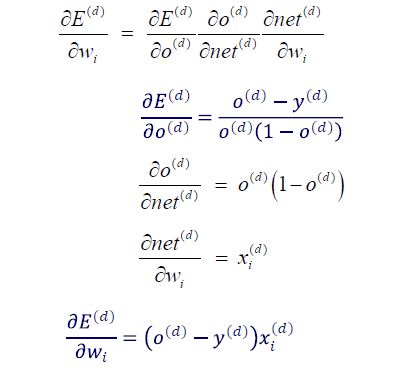이번에도 마찬가지로 chain rule을 통해서 하나씩 구한 뒤에 곱해주면 된다. 결과만 보면 이전 예시와 동일한 derivative 결과를 보이고 있다. 여기서 이야기할 수 있는 것은 linear function과 SSE를 objective function으로 사용하는 조합과 sigmoid function과 cross-entropy를 objective function으로 사용하는 조합은 동일한 derivative를 얻는다는 것이다. 그리고 이들은 실제로 perceptron을 학습할 때 사용하는 식과 동일하다. 비록 activation function이 step function과 같이 smooth하지 않음에도 model parameter를 update하는데 동일한 gradient를 사용할 수가 있다.

Backpropagation

이제 우리는 gradient를 어떻게 구하는지 알게 되었다. 그리고 gradient는 우리에게 방향을 말해주게 된다. 그러면 이제 어느 방향인지 알게 되었으니 그 방향으로 움직일 필요가 있다. 이전까지는 single-layer network에서 gradient descent를 어떻게 사용하는지 알았다면, 이제부터는 multi-layer network에서 어떻게 사용하는지 알아보고자 한다. Multi-layer network에서는 모든 weight마다 gradient를 구해줄 필요가 있다. 이를 위해서 backpropagation을 이용해서 output unit들로부터 hidden unit들까지 gradient를 역으로 구해가면서 weight를 update하고자 한다.

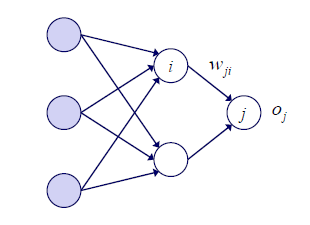Backpropagation을 자세하게 알아보기 위해서 online case를 통해 알아보고자 한다. Node $i$ 다음에 node $j$가 있지만 weight는 $w_{ji}$로 표기해서 사용하고자 한다. 이는 error를 이용해서 뒤에서 앞으로 backpropagation을 통해서 weight를 update하기 때문이다.

각 weight는 gradient와 learning rate의 곱인 $\Delta w_{ji}$에 의해서 update 될 것이다. $\Delta w_{ji}$는 model에서 weight를 얼마나 update 해줘야하는지를 설명해준다. 그리고 여기서 gradient $\frac{\partial E}{\partial w_{ji}}$는 chain rule에 의해서 구해줄 수 있다.

그리고 가장 일반적인 조합으로 sigmoid function과 cross-entropy를 사용한다고 해보자. 그리고 $j$가 output unit인 경우와 hidden unit인 경우를 따로 생각해보고자 한다. $j$가 output unit인 경우에는 $\delta_j$는 $y_j-o_j$가 될 것이다. $j$가 hidden unit인 경우에는 그 다음에 $k$ unit이 있다고 생각해보자. 이 경우에는 $\delta_j$가 조금 다르게 정의가 될 것이다. $\delta_k$는 error term으로 간주가 되고, output node와 $k$의 error를 계산하게 되므로 $\sum_k \delta_k w_{kj}$가 될 것이다. 여기서 $w_{kj}$와 함께 계산이 된 뒤에 다음으로 넘어가 $\delta_j$는 $w_{ji}$를 계산하는데 사용될 것이다. $k$번째 layer에 있는 unit들마다 error가 존재할 것이고, 이들을 모두 더해줌으로써 다음 $j$번째 layer에서 사용이 될 것이다. 더 나은 이해를 위해서 다음의 visualization 과정을 보도록 하자.

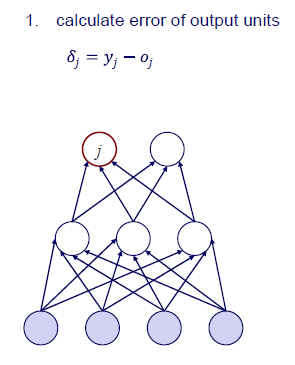먼저 output unit의 error를 계산해야 한다. 여러개의 output node가 있을 것이고 이로부터 error를 $y_j-o_j$로 구할 수 있다.

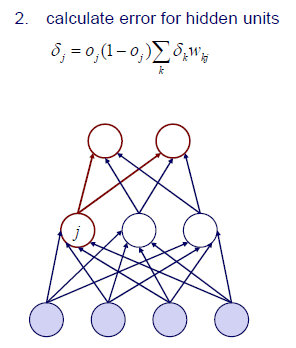그 다음에는 hidden unit들이 존재할 것이다. 여기서는 $k$번째 layer의 output unit들의 error를 모두 고려해 다시 error를 구할 수가 있다. 그렇게 $k$번째 layer의 전체 error를 $\sum_k\delta_kw_{kj}$와 같이 구한 다음에 backpropagation을 위해서 $o_j(1-o_j)$까지 곱해주면 된다.

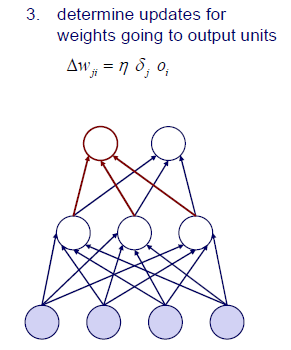그렇게해서 weight를 얼마나 update해줄지 $\Delta w_{ji}$를 구할 수가 있다. 여기서 $o_i$는 $j$번째 layer로 향하는 $i$번째 layer의 input을 이야기 한다.

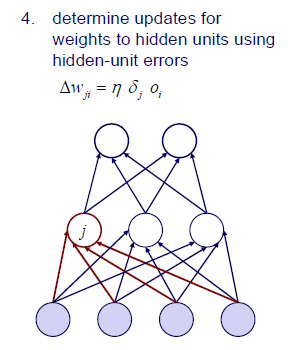마찬가지로 진행해주면 된다. 그래서 backpropagation은 objective function과 activation function에 따른 particular derivative이다. Gradient descent와 backpropagation은 이러한 function들이 미분 가능한 다른 경우에도 적용이 된다. Gradient만 구할 수 있으면 gradient descent와 backpropagation이 항상 가능하고 update가 가능하다는 이야기다.