[데이터마이닝] Support Vector Machine (SVM)

Support Vector Machine(SVM)은 유명한 binary classifier 중 하나이다. Deep learning이 본격적으로 알려지기 전까지는 성능도 좋고 많이 사용되었다.

Some Key Vector Concepts

SVM을 알아보기 전에 먼저 dot product가 무엇인지 알아야 한다. Dot product는 두 vector 사이의 element-wise product와 summation을 한 결과이다.

그리고 norm이 무엇인지도 알아야 한다. 가장 대표적인 2-norm(Euclidean length)는 다음과 같이 계산할 수 있다.

Support Vector Machine

이 두가지 개념을 알고 있으면 SVM을 디자인할 수 있다.

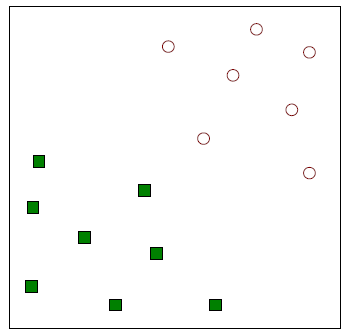SVM은 binary classifier이기 때문에 위와 같이 두 그룹의 data가 필요하다. SVM이 하고자하는 것은 위와 같은 data를 classification하고자 하나의 직선을 그리는 것이다. 여기서 이 직선을 linear hyperplane 혹은 decision boundary라고 한다.
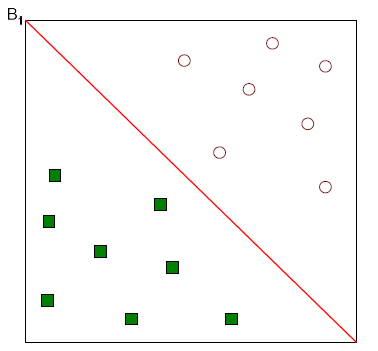위와 같이 그릴 수 있을 것이다.

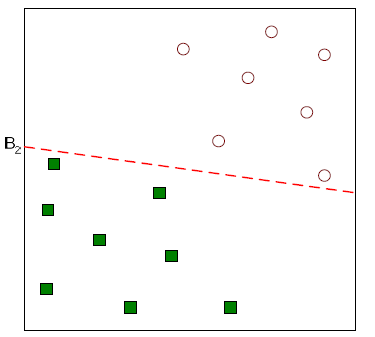혹은 위와 같이 그릴 수도 있을 것이다.

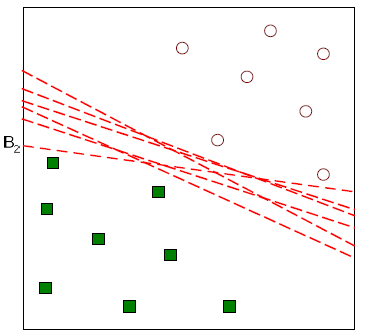Data를 나눌 수 있는 직선은 무수히 많이 존재할 것이다. 그렇다면 어떠한 직선이 best solution이 되는 것일까? 이 질문에 대한 대답을 하고자 하는 것이 바로 SVM이 원하는 것이다.

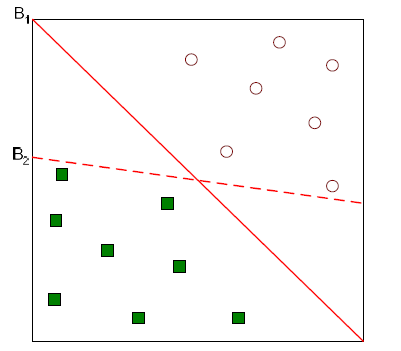위와 같이 $B_1$과 $B_2$가 있을 때 어느 직선이 더 classifier로서 역할을 잘한 것일까? 일반적으로 많은 사람들이 $B_1$이 더 나은 결과라고 이야기할 것이다. 왜냐하면 사람들은 margin이 생겼을 때 더 편안함을 느끼기 때문이다. $B_2$와 같이 data에 딱 붙어있는 결과를 사람들은 선호하지 않을 것이다.

Decision boundary로부터 가장 가까운 data와의 distance가 가까운 것보다는 먼 것을 선호하게 된다. 즉, margin이 더 큰 $B_1$을 선호하는 것이다. 그래서 우리의 목표는 이러한 margin을 최대한으로 만드는 hyperplane을 찾는 것이다.

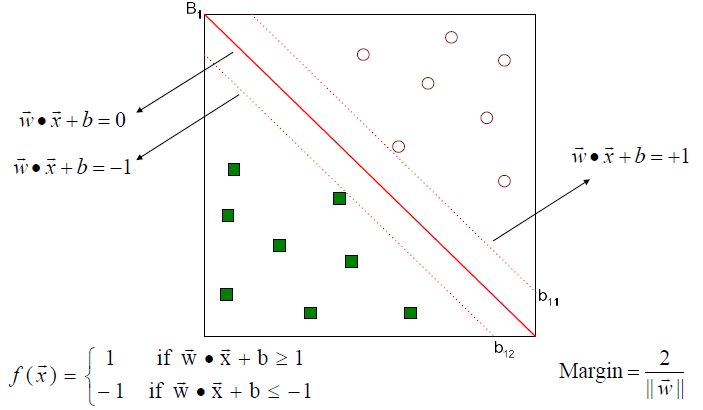Margin을 최대한으로 만들기 위해서 optimization problem으로 식을 정리해야 한다. 그러기 위해서는 margin을 먼저 정의해야 한다. Margin을 정의하기 전에 먼저 임의로 2개의 평행한 직선을 정의해야 한다. 가운데 원래의 decision boundary가 있다고 하면 이와 평행하게 2개의 직선을 정의하는 것이다. Decision boundary를 $wx+b=0$이라고 정의한다면 평행한 두 직선은 $wx+b=\pm1$로 정의할 수 있다. 그래서 새로운 sample에 대해서 계산한 식이 1보다 크면 1로, -1보다 작으면 -1로 classification하는 구조이다.

그렇다면 여기서 margin을 위와 같이 정의한 이유에 대해서 생각해봐야 한다. Margin을 보면 slope $w$의 norm과 관련된 식으로 되어있는 것을 볼 수 있다. 그리고 우리는 이러한 margin 식을 최대로 만들어야 하는 것이다. 그래서 margin을 최대로 만드는 parameter를 찾을 필요가 있다.

Four Key SVM Ideas

SVM과 관련해서 중요한 아이디어들을 보려고 한다.

1. Maximize the margin
우리는 아무 hyperplane이나 선택하지 않을 것이다. Margin을 최대로 만드는 optimal hyperplane을 찾을 것이다.

2. Penalize misclassified examples
Decision boundary를 그린다고 했을 때 오분류 된 sample들에 대해서 일종의 penalty를 주고자 한다.

3. Use optimization methods to find model
Model을 찾는데 있어서 optimization method를 사용하고자 한다. 특히 linear programming이나 quadratic programming 기법을 통해서 model을 찾을 것이다.

4. Use kernels to represent nonlinear functions and handle complex instances (sequences, trees, graphs, etc.)
위에서 본 예시는 직선으로 data를 나누는 것이었다. 그렇다면 직선으로 나누지 못하는 data들은 어떻게 할 수 있을까? 바로 kernel을 사용해서 nonlinear function을 만들고 복잡한 예시들에 대해서 적용하고자 한다.

Linear Separator Learning (revisited)

우리는 perceptron을 공부하면서 linear separator에 대해서 알아보았다. Instance가 들어오면 linear equation을 통해서 그 결과를 확인하고 label을 부여하는 식이었다. 만약 instance가 제대로 classification이 되었는지 확인하려면 $y(w^Tx+b)>0$ 식에 넣고 확인해보면 된다. Label이 1이라면 instance가 제대로 classification 되었을 경우에는 직선 위에 있을 것이기 때문에 곱하면 양수가 될 것이다. 반대로 label이 -1이라면 classification 결과가 맞다면 직선 아래 쪽에 있을 것이기 때문에 이때도 곱하면 양수가 될 것이다.

Large Margin Classification

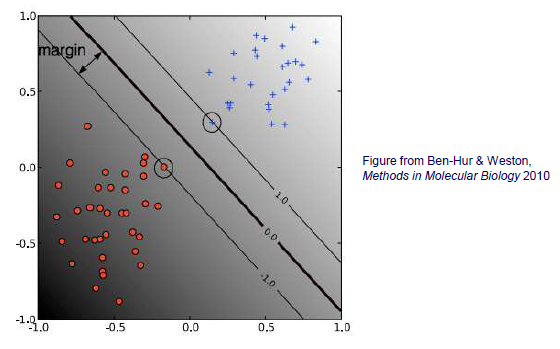Linearly separable한 training set이 주어졌을 때, instance들을 positive와 negative로 나눌 수 있는 hyperplane은 무수히 많이 존재한다. 이러한 가정 속에서 어떠한 hyperplane을 선택해야 하는 것일까? SVM은 많고 많은 hyperplane 중에서도 margin을 최대한으로 만드는 것을 찾으려고 할 것이다.

The Margin

Margin을 최대한으로 만들어야 하기 때문에 먼저 margin이 어떻게 정의가 되는 것인지 좀 더 자세하게 보려고 한다.
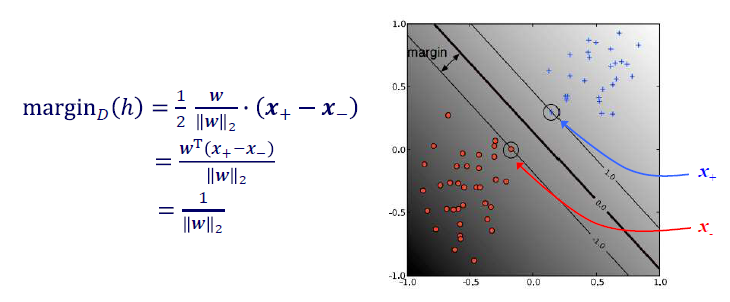Training set $D$에 대해서 hyperplane $h$를 찾는다고 가정할 것이다. 그리고 $x_+$를 positive instance들 중에서 hyperplane에 가장 가까운 instance로, $x_-$를 negative instance들 중에서 hyperplane에 가장 가까운 instance로 정의할 것이다. 그리고 $w^Tx+b=0$이나 $c(w^Tx+b)=0$이나 동일한 hyperplane을 정의하기 때문에 우리는 $w$의 normalization을 선택하는데 있어서 어느것을 택해도 상관이 없다. $w$를 scaling하는데 있어서 어떠한 값을 곱해도 상관이 없다는 것이다.

그러면 이제 margin이 왜 위와같이 식이 정의되는지 알아볼 것이다. $w$를 $w$의 norm으로 나눈 것은 단순히 normalization을 한 것이다. $x_+$와 $x_-$를 뺀 결과는 hyperplane에 수직인 vector가 된다. 결국 우리는 수직인 이 vector와 hyperplane의 slope를 inner product했다고 볼 수 있다.

The Hard-Margin SVM

이제 우리는 위에서 정의 된 margin을 주어진 constraint와 함께 최대한으로 만들어야 한다. 어떠한 것을 최대로 만든다는 것은 그 역수를 최소로 만든다는 것과 동일하다. 그래서 위에서 objective function을 minimization으로 바꿔준 것이다. 우리는 결국 margin을 최대로 만드는 이 문제를 constrained optimization problem으로서 해결하고자 하는 것이다. Hyperplane이 $w,b$로 인하여 결정이 되기 때문에 우리는 margin의 역수를 최소한으로 만드는 $w,b$를 찾고자 한다. 일단 이렇게 식을 세우긴 했는데 그렇다면 이 식을 어떻게 풀어야 하는 것일까? 대표적인 optimization solver를 이용해서 해결하면 된다. 옛날에는 이러한 optimization problem을 해결하는 것이 매우 어려운 주제였다. 하지만 이제는 solver를 이용하면 쉽게 solution을 구할 수가 있다.

The Soft-Margin SVM

지금까지는 hyperplane을 기준으로 모든 sample들이 완벽하게 linearly separable했다. 하지만 이는 이상적인 경우고 만약 모든 sample을 완벽하게 나누지 못한다면 어떻게 해야할까? 이 경우에는 위에서 세운 식을 사용해서는 안된다. 이러한 경우에는 soft-margin SVM을 사용해서 해결하면 된다. 위의 경우는 hard-margin SVM이라고 한다. 그 이유는 모든 training sample들이 constraint을 만족해야 했기 때문이다. Soft-margin SVM에서는 그 조건을 다소 느슨하게 하는 것이 핵심이다.
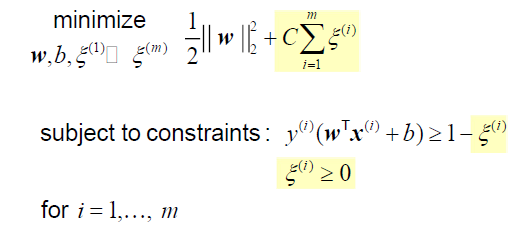이를 위해서 우리는 slack variable $\xi$을 사용하려고 한다. 기존의 margin의 역수를 minimization하는 것은 동일하다. 여기에 slack variable을 이용한 term을 추가해서 어느정도 error를 용인해주려고 한다. 일단 우리는 몇개의 sample 정도는 hyperplane을 가로질러도 허용해주려고 하는 것이 soft-margin SVM의 목적이다. 그리고 두번째 term이 그 역할을 해줄 수 있다.

Objective function이 바뀌었기 때문에 constraint도 바뀔 필요가 있다. Hard-margin SVM의 constratin에서 slack variable을 추가함으로써 어느정도 error를 허용해줄 것인지 정할 수가 있다. 얼마나 sample이 넘어가도 괜찮을지를 $\xi$가 말해주는 것이다. 그리고 $\xi$는 음수가 되면 안된다. 그러면 hyperplane의 반대편에 정의가 되기 때문에 원하는 목적을 달성할 수 없게 된다.

그리고 중요한 것은 바로 objective function의 $C$이다. $C$는 margin을 최대로 만들 것인지(첫번째 항)와 아니면 slack을 최소한으로 만들 것인지(두번째 항)에 대해서 상대적인 중요성을 결정해줄 수 있는 hyper-parameter이다. Margin이 중요한지 error가 중요한지를 결정해주는 것이다. 만약 margin을 키우는 것이 중요하면 $C$는 작아지게 될 것이다. 반대로 error를 줄이는 것이 중요하면 $C$는 커지게 될 것이다. $C$가 커진다는 것은 $\sum\xi$의 중요도가 상대적으로 낮아지게 되는 것이고, 반대로 $C$가 작아지면 $\|w\|$의 중요도가 상대적으로 낮아지게 될 것이다.

The effect of C in a soft-margin SVM

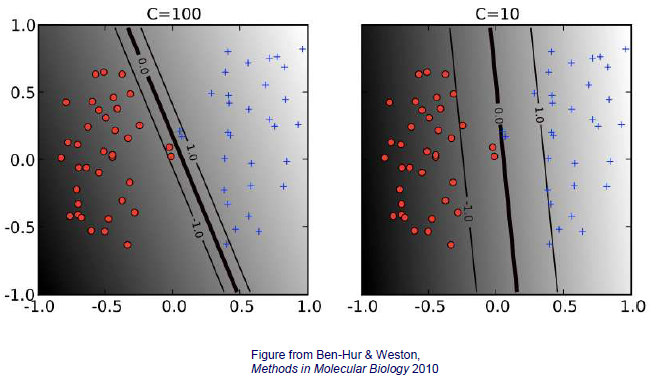위의 graphical illustration을 통해서 만약 $C$가 커지게 되면 margin이 작아지고 error를 허용하지 않는 것을 볼 수 있다. 반대로 $C$가 작아지면 margin이 강조되고 error를 허용하는 것을 볼 수 있다. 그렇다면 어느 것이 더 나은 결과일까? 이는 선택하는 사람의 생각에 달려있다.

Hinge Loss

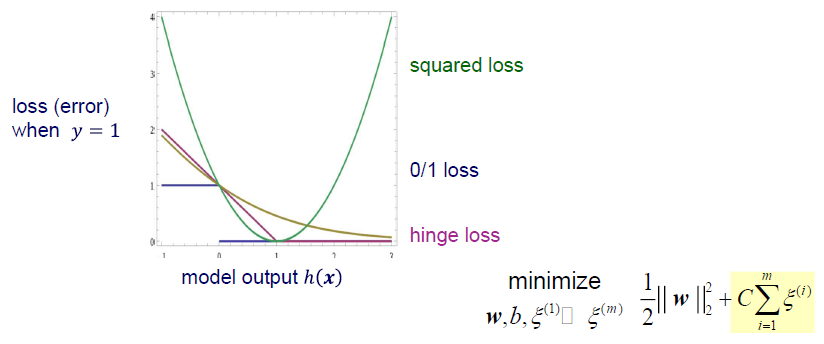NN를 이야기할 때 sqaured loss나 cross-entropy loss를 줄여야하는 것을 알고있다. 그렇다면 soft-margin SVM은 어떠한 loss를 줄여야하는 것일까? 바로 여기서 hinge loss를 사용하게 된다. Hinge loss에서는 조건을 위반하는 경우에만 error가 쌓이게 된다.

Non-Linear Classifiers

그렇다면 non-linear classfier는 어떻게 다뤄야하는 것일까? 조금 전에 살펴본 soft-margin SVM이 대표적인 예시 중 하나이다. Outlier가 존재하거나 특정 sample들이 linearly separable하지 않다면 직선으로 이를 해결할 수 없다. Soft-margin SVM의 경우는 어느정도 error를 허용해준 것이고, non-linear한 경우를 다루기 위해서는 좀 더 정확한 방법들이 필요하다. 아무래도 직선으로 나누기보다는 곡선으로 나누는 것이 더 정확할 것이다. 그래서 이제부터 우리는 kernel을 사용하려고 한다.

Kernel $\phi$는 data를 linearly separable하게 할 수 있는 고차원의 공간으로 data를 보낸다고 생각하면 된다. 여기서 핵심은 data를 또 다른 공간으로 mapping하는 것이다. 이를 위해서는 적절히 좋은 mapping function을 선택해야 한다. 다음은 quadratic space 예시이다.

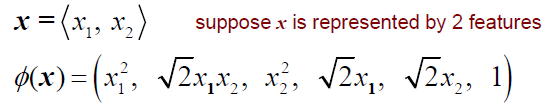2차원에서 data $x$가 linearly separable하지 않은 경우에 quadratic kernel을 이용해서 data를 mapping 해주는 것이다. $x_1,x_2$를 quadratic function에 집어넣어 2차원에서 6차원으로 보내는 예시이다.

여기서 핵심은 training sample들이 linearly separable한 경우에는 SVM을 통해서 classification하면 된다. 하지만 불가능한 경우에는 다른 공간으로 mapping해서 classification을 할 수가 있다. 그러면 slope가 2차원이었던게 6차원으로 변할 것이다.

SVM with Polynomial Kernels

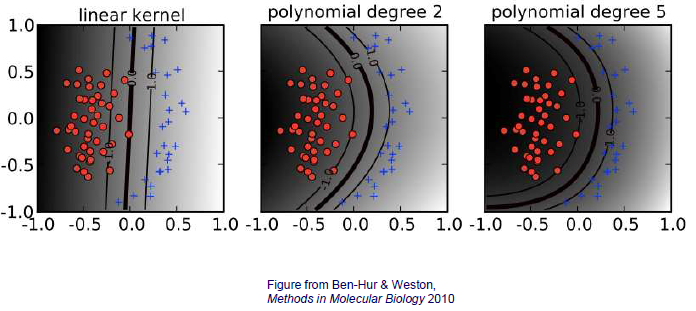Mapping function $\phi$가 polynomial kernel인 경우를 알아보려고 한다. 만약 우리가 linear decision boundary를 그린다고 한다면, data로부터 직선까지의 수직인 거리가 error가 될 것이다.

그렇다면 이번에는 degree가 2인 polynomial kernel을 보도록 하자. 우리는 기본적으로 polynomial kernel을 이용해서 data를 고차원으로 mapping하게 된다. 우리는 $x$를 polynomial function에 넣어 $\phi(x)$를 얻게 된다. 그러면 이제 decision boundary $\hat{w}$를 학습하게 되어 다시 원래 space의 $w$로 되돌아오게 된다. 그러면 위와 같이 곡선의 decision boundary를 얻게 될 것이다. 현재 space에서의 이 곡선은 $\phi$로 mapping 했던 고차원에서는 직선의 형태를 보였을 것이다. 고차원에서 직선으로 학습이 되었던 decision boundary를 현재 space로 가져와 곡선으로 바꿀 수 있게 된 것이다. 그리고 이 곡선과 data의 거리를 error라고 했을 때, error가 줄어들 수 있다. Polynomial degree를 높이게 되면 그만큼 error를 더 줄일 수도 있는 것이다. 아무래도 degree가 높아진다는 것은 그만큼 data가 복잡한 형태를 보인다는 것을 의미하게 된다. 즉, data가 overfitting 될 가능성이 커지는 것을 의미한다.

The Kernel Trick

이번에는 kernel trick이라고 하는 개념을 볼 것이고, 이는 매우 중요한 개념이다. 우리는 linearly separable하지 못한 data $x$에 대해서 $\phi$를 이용해 고차원으로 mapping 시켜 주었다. 그러면 고차원에서 $\hat{w}$를 학습하게 되고, 이는 곧 원래의 space에서 $w$를 학습하게 되는 것으로 이어지게 된다. 아무래도 고차원에서 $\hat{w}$를 학습하는 것이 원래의 space에서 $w$를 학습하는 것보다 복잡할 것이다.

그렇다면 여기서 $\phi$는 어떠한 것을 사용해야하는 것일까? 이는 사용하는 사람의 선택에 따라 달라질 수 있다. 여기서 일반적으로 이러한 non-linear mapping은 잘 확장되지 않는다. 그 이유는 아무래도 보통 저차원에서 고차원으로 가는 것이 대부분 어려운 문제이기 때문이다. 반대로 고차원에서 저차원으로 가는 것은 쉬울 것이다. 그래서 사람들이 생각해낸 solution이 바로 kernel trick인 것이다. 2개의 고차원 mapping 사이의 dot product는 kernel function으로 가능할 수 있다. 이를 이해하기 위해서 다음의 quadratic kernel 예시를 보도록 하자.
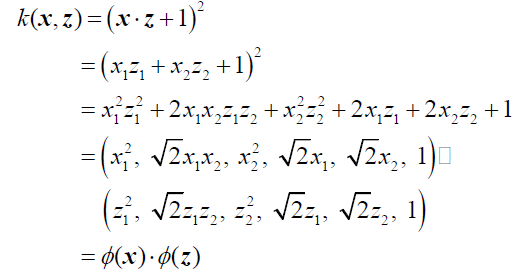이 kernel function은 $x$와 $z$를 inner product하여 1을 더하고 제곱을 취하게 된다. 쉬운 이해를 위해서 $x$와 $z$를 2차원이라고 가정할 것이다. 식을 전개하다보면 어느순간 2개의 vector의 곱으로 정의되는 것을 볼 수 있다. 구조가 같은 2개의 vector를 통해서 $\phi$를 정의할 수 있게 된다. 즉, 2차원 data로부터 mapping function을 고차원에서 정의한 것이다. 우리가 한 것은 2차원의 data를 정리해준 것 뿐인데 6차원의 kernel을 정의할 수 있게 된 것이다. 이것이 바로 kernel trick이다. 원래는 2차원의 $x$를 고차원으로 보내 parameter를 학습해야 하지만, 이럴 필요가 없이 이러한 kernel trick을 이용하면 inner product만 했을 뿐인데 간단하게 mapping 시킬 수가 있게 되었다.

그래서 우리는 kernel을 이용하여 instance들을 고차원의 space에 명시적으로 mapping 시킬 필요없이 dot product를 계산할 수 있다. 이전에 우리는 classifier를 $w$와 $x$의 dot product로 구할 수 있었다. 이 dot product는 qudratic kernel과 같은 kernel function을 이용하면 이 kernel이 고차원에서의 dot product 결과를 얻게 해주는 것이다. 결국 고차원에서의 dot product는 신경쓸 필요가 없고 원래의 space에서 kernel을 이용한 dot product만 신경쓰면 되는 것이다. Kernel trick의 장점은 모든 mapping 과정을 우회할 수 있다는 것이다. 그럼 이제 SVM의 training process를 보도록 하자.

$m$개의 sample로 이루어진 $D$가 주어졌다고 했을 때, weight vector $w$가 training instance들의 linear combination으로 표현될 수 있다고 가정해보자.

그러면 우리는 linear SVM을 다음과 같이 나타낼 수 있다. Linear SVM은 $w$와 $x$의 dot product이기 때문에 다음과 같이 식이 정리된 것이다.

Non-linear SVM은 식에서 $x$를 mapping해주기만 하면 된다. Mapping function $\phi$의 곱은 결국 kernel에 training data를 넣어준 것과 같아지게 된다. $\phi$를 사용하면 data를 고차원에 mapping해주게 되지만, kernel을 사용하게 되면 이러한 과정을 생략하고 현재 space에서 쉽게 구할 수 있게 되는 것이고 더 간단해진다.

The Primal and Dual Form of Hard-Margin SVM

Hard margin SVM이 풀어야하는 optimization problem을 primal form으로 나타낼 수 있고, 이를 정리하여 dual form으로 변형할 수도 있다. 만약 학습해야하는 $w$를 $\sum\alpha_i x_i$로 대체하게 되면 primal form이 dual form이 되는 것이다. Primal form을 풀고자 한다면 모든 $w$를 계산해야 하기 때문에 복잡해질 것이다. 그래서 dual form을 풀면 간단하게 해결할 수 있다. Dual form에서는 $w$를 대체했기 때문에 구해야하는 것이 coefficient로 바뀌게 된다. 그리고 이러한 과정은 상대적으로 primal form에서 $w,b$를 찾는 것보다 간단할 것이다.

여기서 핵심은 우리가 구해야 하는 $\alpha$들은 음수면 안되고 $y$와 곱해서 그 합이 0이 되어야 한다. 이 constraint가 의미하는 것은 $\alpha$가 sparse하다는 것을 의미한다. Margin을 정하는데 있어서 우리는 모든 training instance들이 필요한 것이 아니다. Decision boundary를 기준으로 2개의 직선을 그리는데 약간의 instance들만 있으면 된다. Slope를 알고 가까운 instance에 부딪히게 되면 2개의 직선을 충분히 구할 수 있기 때문이다. 이러한 이유 때문에 $w$를 결정하기 위해서 $\alpha$가 sparse해야 하는 것이다.

Primal problem은 모든 instance들을 동원해서 아마도 고차원의 $w$를 구해야 할 것이다. 하지만 primal form을 dual form을 바꾸게 된다면 objective function이 바뀌게 될 것이고, 식 안에서 training sample 간 dot product를 포함하게 된다. 그러면 dual form에서 sparse하고 음수가 아닌 $\alpha$를 찾으면 될 것이다. 이렇게 우리는 구하기 어려운 $w$ 대신에 구하기 쉬운 $\alpha$를 구하면 된다.

The Dual Form with a Kernel (Hard Margin Version)

이번에는 kernel을 이용한 dual form을 알아볼 것이다. Primal form에서 constraint를 보면 기존의 $x$에서 $\phi(x)$로 바뀐 것을 볼 수 있다. 자연스럽게 dual form도 objective function이 바뀌게 되고 아마 mapping function의 dot product인 $\phi(x^{(i)})\phi(x^{(k)})$가 될 것이지만 우리는 kernel trick을 알고 있기 때문에 위와 같이 kernel function을 사용할 수 있게 된다. 이는 우리가 고차원에서 non-linear SVM을 학습한다고 했을 때, 고차원에서는 sample들이 linearly separable하다는 가정이 존재한다. 여기서 핵심은 dual form으로 SVM을 푼다고 했을 때 고차원의 vector간 inner product가 동반되어야 한다는 것이다. 그리고 이는 저차원에서의 kernel로 대체가 된다는 부분이 중요한 것이고, kernel trick이 중요한 이유이다.

Support Vectors

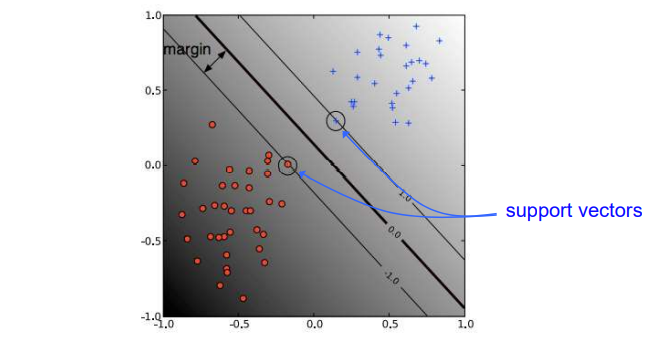Dual formulation의 solution은 training instance들의 sparse linear combination이다. 그리고 여기서 $\alpha$가 양수인 instance들을 우리는 support vector라고 하는 것이다. Support vector는 결국 margin boundary 위에 있는 instance들을 의미한다. 실질적으로 margin을 최대로 만드는데 있어서 모든 training instance들이 필요한 것이 아니다. 결정하는데 중요한 것은 오로지 support vector에 해당하는 것들이다. 여기서 중요한 부분은 $\alpha$가 0인 instance들을 없애더라도 그 solution이 바뀌지 않는다는 것이다. 즉, support vector를 제외한 training instance들은 사실상 크게 중요하지 않다. SVM은 개념적으로 deep learning과는 상반된다. Deep learning은 아무래도 잘 동작하기 위해서는 충분한 양의 training data가 필요하다. 하지만 SVM은 비록 training data가 충분하지 않아도 잘 동작한다는 특징이 있다.

The Kernel Matrix

때로 우리는 kernel matrix를 구성해서 사용해야 한다. Gram matrix라고도 불리는 kernel matrix는 training set에 존재하는 instance들에 대한 similarity를 설명할 수 있다. 다음과 같이 모든 instance pair를 kernel에 넣어 matrix를 구성한 것이다.
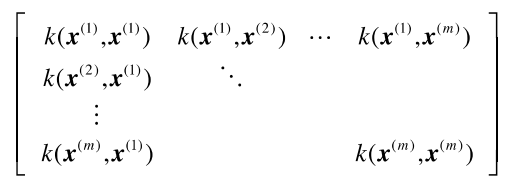이 matrix가 Gram matrix라고 불리는 이유는 optimization에서 사람들은 일반적으로 dual formulation을 풀라고 하는데 이때 pair-wise similarity가 매우 많이 필요하기 때문이다. 그래서 사람들은 이 kernel matrix를 미리 구해두고 lookup table로서 사용하게 된다. Optimization 과정에서 input으로서 제공되는 training set에 대한 정보를 제공해주는 것이 바로 kernel matrix이다.

Some Common Kernels

SVM에서 Gaussian kernel은 매우 중요한 kernel이며, radial basis function(RBF)로도 불리곤 한다. 2개의 vector 사이의 distance에 scale 값을 곱해서 exponential을 취해준 것이다.

The RBF Kernel

RBF kernel을 위한 feature mapping function $\phi$의 차원은 무한할 수 있다. RBF kernel에 $x,z$를 대입한 것은 마찬가지로 고차원의 $\phi(x)\cdot\phi(z)$와 동일하다. 그럼 이제 왜 차원이 무한할 수 있는지 이야기해보고자 한다.
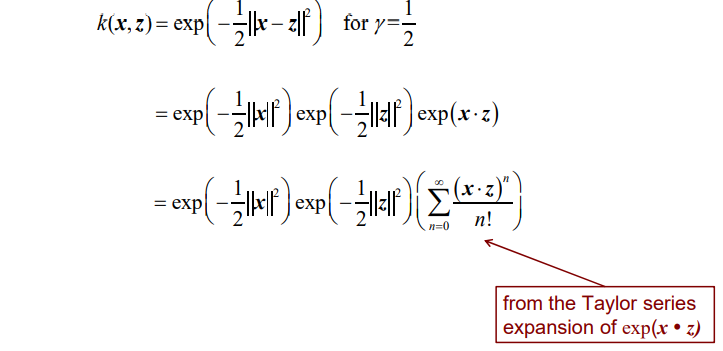RBF kernel function $k(x,z)$에 $\gamma$ 값을 1/2라고 설정했다고 해보자. 그러면 이 식을 정리해보면 3개의 exponential term으로 나눌 수가 있다. 앞의 2개의 term은 scalar 값이지만 마지막 term은 그렇지 않다. Taylor series를 이용하여 exponential function을 정리할 수가 있다. 그러면 $x$와 $z$의 dot product를 무한히 더하는 식이 만들어지게 된다. 우리는 $\gamma$ 값을 통해서 exponenetial function의 slope를 조절할 수 있다. 결국 마지막 term에서 무한히 dot product를 구하고 더하기 때문에 RBF kernel의 차원이 무한해질 수 있다는 것이다. 그리고 얼마나 많이 무한한 차원을 mapping하는지가 SVM에 영향을 미치게 될 것이고, 이 속도를 $\gamma$를 통해서 조절하게 되는 것이다.

The RBF Kernel Illustrated

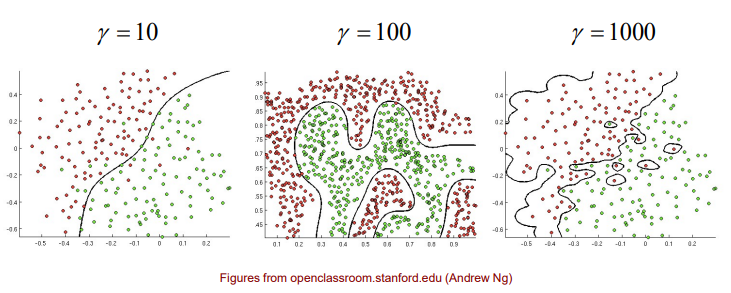RBF kernel에서 $\gamma$ 값이 작아지게 되면 decision boundary가 덜 flexible 하게 될 것이고, classifier에 non-linearity가 어느정도 존재하게 될 것이다. 반대로 $\gamma$값이 엄청 커지면 어떻게 될까? 동일한 data에 대해서 $\gamma$ 값이 엄청 커지게 되면 classifier는 outlier 마저도 정확하게 classification을 수행할 것이다. 즉, 매우 복잡한 decision boundary를 형성하게 되는 것이다. 이러한 경우에 문제는 overfitting이 되어 새로운 data가 들어왔을 때 제대로 역할을 수행하지 못할지도 모른다.

What Makes a Valid Kernel?

Kernel이 valid kernel이 되기 위해서는 다음을 만족하는 $\phi$가 존재해야 한다. 저차원에서 kernel operation을 할 수 있고 고차원에서 mapping function 사이의 dot product가 가능한 상태에서 이 둘이 같아지게 되면 우리는 valid kernel이라고 하는 것이다.

그리고 이는 symmetric function $k(x,z)$에 대해서 kernel matrix $k$가 모든 training set에 대해서 positive semidefinite한 경우를 이야기하기도 한다. 우리는 이를 Mercer's theorem이라고 한다. Positive semidefinite은 다음과 같이 어떠한 vector에 대해서도 만족해야 한다.

그리하여 kernel matrix가 positive semidefinite 조건을 만족하게 된다면 이를 SVM에 사용할 수 있는 것이다.

Support Vector Regression

지금까지 SVM은 classification task를 다루고 특히 binary classification을 위한 classifier로서 역할을 했었다. 하지만 이러한 SVM은 classification 뿐만 아니라 regression task도 다룰 수가 있다. Margin을 최대로 한다는 SVM의 아이디어로부터 regression task에도 적용할 수 있다는 것이다. 우리는 $\varepsilon$를 특정 margin 내에서 얼마나 많은 error를 regressor가 용인할 것인지 정하는 측도로서 사용할 것이다.
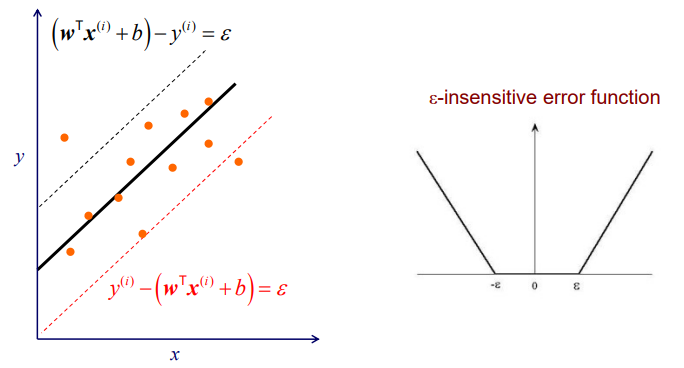Training sample들이 있을 때 하나의 직선을 그리면서 data regression을 수행할 수 있다. 그리고 평행한 두 직선을 통해서 margin을 정의할 수 있다. 그리하여 모든 training sample들이 margin 내에 최대한 존재하도록 만들 것이다. 우리는 그래서 두 직선 밖에 있는 training sample에 대한 error를 최대한 줄이고자 한다. Training sample들이 margin 내에 존재하면 error는 0가 될 것이다. 범위 밖에 sample이 존재할 때마다 error가 증가하게 될 것이다.

마찬가지로 error term에서는 hinge loss를 사용하여 boundary로부터 얼마나 멀리 떨어져있는지가 error를 결정하게 된다.

Comments

정리하자면 우리는 SVM에서 margin을 최대로 만들기 위해서 global optimal solution을 찾을 수가 있다. Global solution이 존재한다는 점이 매우 중요한 부분이다. 왜냐하면 problem 자체가 convex problem이고 이는 critical point가 존재하기 때문이다. 그리하여 multi-layer NN과는 대조적으로 local minima가 존재하지 않는다. Multi-layer NN보다 SVM이 더 설명가능한 model이다. 물론 training set이 충분히 존재하는 경우에는 NN가 훨씬 더 성능이 좋을 것이다.

ANN과 SVM을 좀 더 비교해보자면 SVM은 sparse한 $\alpha$를 풀려고 하는 반면 ANN은 dense한 weight parameter $w$를 풀려고 한다. SVM이 더 낫다고 볼 수 있다. Training set의 관점에서 SVM은 상대적으로 적은 양이 필요하지만 ANN은 충분히 많은 양이 필요하다. Learning process의 관점에서 SVM은 convex problem을 풀기 때문에 항상 global optimal solution이 존재하는 반면 ANN은 local minima가 많이 존재한다. 그리고 SVM은 margin을 최대로 만들려고 하지만 ANN은 error를 최소로 만들려고 한다. 추가적으로 non-linearity 관점에서 SVM은 kernel을 사용할 수 있지만, ANN은 hidden layer를 다수 사용하게 된다. 개념 자체가 완전히 다른 것이 SVM과 ANN이다. SVM이 훨씬 더 좋아보이지만 현실에서는 data의 양이 매우 많기 때문에 ANN을 사용하는 것이 더 나은 경우가 다수이다.