[데이터마이닝] Similarity and Dissimilarity - Similarity Measures

Similarity Between Binary Vectors

이번에는 binary vector를 가지고 similarity를 알아보고자 한다. Binary vector이기 때문에 그 값은 0 아니면 1로 존재할 것이고, 이는 categorical attribute의 특별한 경우에 해당하게 된다. 여기서는 오로지 2개가 서로 같고 다름만을 설명할 수 있다. 예를 들어 오로지 binary attribute만을 가지고 있는 object $x,y$가 있는 상황을 생각해보자. 그러면 이러한 경우에는 다음의 4가지 경우만 고려하면 될 것이다.

더 자세하게 예를 들어 다음과 같이 vector를 구성하는 element들이 있다고 해보자.

이를 이용해서 우리는 각 element들을 서로 비교를 할 것이다. 왜냐하면 $x$와 $y$가 가질 수 있는 값으로는 오로지 0 아니면 1일 것이고, 각각의 element를 비교하게 되면 그 결과로 오직 4개의 경우만 가능하기 때문이다. 그리고 각각의 결과가 얼만큼 나왔는지가 우리가 고려해야하는 경우들인 셈이다. $f_{01}$과 $f_{10}$의 경우는 각 object들의 dissimilarity를 보고자 하는 것이고, $f_{00}$과 $f_{11}$의 경우는 각 object들의 similarity를 보고자 하는 것이다. 그리고 이들을 이용해서 다음의 2가지 similarity measure들에 대해서 알아볼 것이다.

SMC vs Jaccard

1. Simple Matching

2. Jaccard Coefficients

여기서는 $f_{00}$은 신경쓰지 않고 오로지 $f_{11}$에 대해서만 신경쓰고자 한다. 이는 우리가 오직 non-zero element만이 중요한 정보를 가지고 있다고 판단하기 때문이다. 0이라는 element는 어떠한 의미도 내포하고 있지 않다. 그렇기에 non-zero의 경우만을 고려해서 similarity를 측정하고자 하는 것이다. 그렇기 때문에 Jaccard coefficient의 식을 보면 simple matching과는 다르게 둘다 0이 되는 경우는 제외시킨 것을 알 수 있다.

그렇다면 이러한 similarity measure은 언제 사용하려는 것일까? 사과 image가 있을 때 segmentation을 한다고 가정해보자. 특히 사과와 배경을 구분한다고 했을 때 만약 배경에게 사과냐고 물어봤을 때 no라고 답할 수가 있을 것이다. 그렇기 때문에 segmentation을 통해서 사과를 1 배경을 0으로 두고 진행할 수 있는 것이다. 즉, foreground로 존재하는 사과라는 object가 중요하다는 것이고, 이러한 segmentation algorithm을 이용하고자 machine learning을 학습하게 된다면 Jaccard coefficient를 사용하게 될 것이다. 다음은 SMC와 Jaccard를 비교하기 위한 간단한 예시이다.
$x$와 $y$가 위와 같이 주어졌을 때, 각각의 경우에 대해서 계산 할 수 있을 것이다. 이때 Jaccard coefficient 값이 0이 나오게 되고, 이는 $x$와 $y$가 similar하지 않다는 것을 우리에게 말하고 있는 것이다. SMC와 Jaccard 값이 다르다는 것은 동일한 object에 대해서 서로 다른 관점에서 similarity를 측정했기 때문이다.

Cosine Similarity

Cosine을 통해서 어떻게 similarity를 표현할 수 있을까? $d_1,d_2$를 각각 document vector라고 한다면, cosine similarity는 다음과 같이 구할 수 있다.

만약 $d_1$과 $d_2$가 동일한 vector라고 한다면 두 vector 사이 각도가 0도가 되어 cosine 값은 1이 될 것이다. 즉, $d_1$과 $d_2$ 사이의 similarity 값은 1이 된다. 이번에는 두 vector가 서로 orthogonal인 경우에는 어떠할까? 이 경우에는 두 vector 사이 각도가 90도가 되어 cosine 값은 0이 될 것이다. 즉, $d_1$과 $d_2$ 사이의 similarity 값은 0이 될 것이다. 그렇다면 만약 각도는 0이지만 길이가 다른 경우에는 어떠할까? 그 답은 바로 "길이는 중요하지 않다"이다. 여기서 중요한 것은 길이가 아닌 방향이다. 우리는 cosine similarity의 식을 통해서 inner product 값을 각각의 길이로 normalization 시켜줌으로써 그 값의 범위를 -1에서 1 사이로 만든 것을 알 수 있다. 이렇게 cosine 값을 통해서 2개의 vector가 서로 연관성이 있는지 없는지를 판단할 수 있다. 다음의 간단한 예시를 보도록 하자.
만약 위의 예시에서 $d_2$를 "2 0 0 0 0 0 0 2 0 4"와 같이 모든 element에 2배를 한다면 결과는 어떻게 바뀔까? 그 결과는 처음의 cos($d_1$, $d_2$)와 여전히 같을 것이다. 값이 커지더라도 normalization하면 커지는 의미는 사라지게 된다. 즉, vector의 길이는 전혀 상관이 없어지게 된다.

Correlation

Correlation 또한 similarity measure 중 하나로, 2개의 object가 서로 연관성이 있다면 correlation similarity를 통해서 확인할 수 있을 것이다. Correlation은 결국 object 사이의 linear한 연관성을 측정하게 된다. Correlation은 covariance를 사용하게 되며, covariance는 다음과 같이 구할 수 있다.

Correlation은 수식으로 확인하면 covariance를 normalization한 결과이다.

위에서 살펴본 covariance 식을 좀 더 확장해서 살펴보면 다음과 같다.

각 object로부터 평균 값을 빼준 뒤에 그 값을 곱해서 $n$번 더한 뒤 $n-1$로 나눠준 것이다. $n-1$로 나눠주는 이유는 bias를 제거해주기 위해서다. Correlation similarity 식을 다시 보면 각각의 standard deviation으로 나눠준 것을 확인할 수 있다. Cosine similarity에서는 각각의 length로 나눠줬다면, 이번에는 standard deviation으로 나눠주었다. 두 similarity는 굉장히 비슷한 구조의 식으로 되어 있는데, 그 이유는 correlation similarity가 linear한 연관성을 다루기 때문이다.

위는 correlation similarity의 scatter plot으로 -1부터 1까지의 similarity 결과를 보여주고 있다. 만약 $x$와 $y$가 완벽하게 correlation이 존재하고, 이 correlation이 negative하다면 첫번째 결과와 같이 data가 linear하게 내려가는 방향으로 분포하고 있을 것이다. 반대로 correlation이 완벽하게 positive하다면 마지막 결과와 같이 linear하게 올라가는 방향으로 분포하고 있을 것이다.

Correlation vs Cosine vs Euclidean Distance

위에서 correlation과 cosine similarity는 수식으로 봐도 상당히 유사한 것을 확인할 수 있었다. 먼저 data가 얼마나 similar한지를 quantification하고 이를 normalization하는 구조였다. 하지만 Euclidean distance는 이들과는 좀 다르다. 그래서 이번에는 이 3가지를 서로 비교해보려고 한다.
Scaling은 특정 값을 곱하는 것이고$(ax)$, translation은 특정 상수를 더하는 것으로$(x+b)$ 이는 offset이라고 생각하면 된다.

1. Scaling

Cosine similarity에서 길이는 중요하지 않았다. 즉, scaling에 invariant하다는 것이다. Correlation 또한 scaling이 중요하지 않다. 그저 서로의 상관 관계만이 중요했다. 하지만 Euclidean distance의 경우 scaling이 중요하다. 길이가 변하게 되면 Euclidean distance 또한 영향을 받게 된다.

2. Translation

만약 translation을 통해서 vector가 이동하게 된다면 어떻게 될까? 먼저, Euclidean distance는 naive하게 distance를 구하기 때문에 그 값은 변하게 될 것이다. 그리고 cosine similarity 또한 사이 각도가 변하기 때문에 결국 방향이 바뀌게 되어 그 결과 또한 변하게 될 것이다. 하지만 correlation의 경우 크게 상관이 없을 것이다. 왜냐하면 $x$가 증가할 때 $y$가 증가하는 상황에서 translation이 이루어져 vector가 이동했다고 하더라도 그 경향성은 변하지 않기 때문이다.

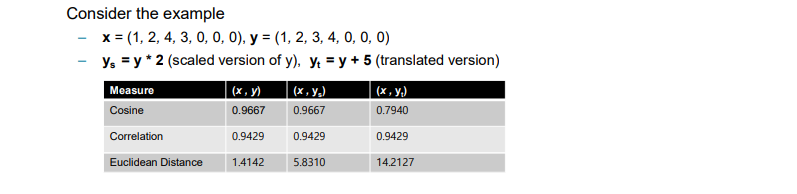위의 예시는 $x$에다가 $y$와 더불어 scaling과 translation을 적용한 $y_s, y_t$를 이용하여 3가지 similarity를 계산한 결과이다. Cosine similarity부터 살펴보면 translation한 결과만 바뀐 것을 볼 수 있다. Correlation의 경우 scaling과 translation에 모두 invariant한 것을 볼 수 있다. 마지막으로 Euclidean distance의 경우 scaling과 translation 모두 바뀐 것을 볼 수 있다.

추가적으로 SMC와 Jaccard의 경우는 어떻게 될까? 이러한 방법들이 실제로 많이 사용될까? 정답은 yes이다. 물론 Euclidean distance가 가장 널리 사용되는 방법인 것은 사실이다. 그러나 보다시피 Euclidean distance가 scaling과 translation에 취약한 것을 확인할 수 있다. 그래도 계속해서 사용되는 이유는 이해하는데 가장 직관적이기 때문이다.

Proper Choise of Similarity Measures

그렇다면 우리는 지금까지 살펴본 similarity measure들 중에서 어떠한 것을 선택해서 사용해야할까? 적절한 proximity measure를 선택하는 것은 domain에 따라 결정하면 된다. Euclidean distance가 널리 사용되고는 있지만 이것이 모든 곳에 사용될 수 있는 것은 아니다. 즉, 우리는 characterization 하고자 하는 data의 성격에 따라서 각자 알맞은 similarity measure를 사용해야 한다.

예시를 보기 전에 각 measure들이 설명할 수 있는 범위에 대해서 간단하게 살펴보려고 한다. Correlation의 경우에는 상관 관계를 살펴보기 위해서 음의 부호까지 필요하다. 그래서 correlation은 $[-1, 1]$의 범위를 가지게 될 것이다. 반면, cosine의 경우에는 $[0,1]$의 범위를 가지게 되며 Euclidean distance는 흔히 생각하는 거리이기 때문에 $[0, \infty]$의 범위를 가지게 된다. 이러한 특징을 생각하면서 예시를 살펴보도록 하자.

Example 1 : Document using the frequencies of words
만약 단어의 빈도수를 이용해서 문서를 비교한다고 해보자. 농구와 축구 문서를 비교하면 공이나 선수 등과 같이 셀 수 있는 서로 비슷한 용어들이 많을 것이다. 이렇게 각 단어들의 빈도수를 확인한 후에 두 문서를 비교한다고 했을 때는 cosine similarity를 사용하면 좋을 것이다. 왜냐하면 cosine similarity의 경우 length와는 아무런 상관이 없기 때문이다. 결국 length에 의해 normalization이 되기에 문서가 몇개든 상관없이 문서에서 단어의 빈도수를 비교하고자 할 때는 cosine similarity를 사용하면 된다.

Example 2 : Temperature in Celsius of two locations
만약 기온이 similar하다면 두 지역이 similar하다고 판단할 수 있을 것이다. 이러한 경우에는 Euclidean distance를 사용하는 것이 적절해 보인다. 왜냐하면 우리는 서로 다르지만 동일한 scale의 object를 비교해야 하기 때문이다. 온도가 similar하기 위해서는 결국 그 크기가 동일해야 한다. 이 경우는 단순하게 동일한 scale을 비교하는 상황이기 때문에 Euclidean distance를 사용하면 충분히 좋은 결과를 가질 수 있다.

Example 3 : Two time series of temperature measured in Celsius
이번에는 시간의 흐름에 따른 온도의 변화가 다른 두 지역을 비교하고자 하는 것이다. 이러한 경우에는 만약 time series의 모양이 similar 할수록 두 time series가 similar하다고 할 수 있다. 여기에는 correlation similarity를 사용하는 것이 적절해 보인다. 왜냐하면 온도가 올라가는 경향성과 내려가는 경향성을 time series를 통해서 확인할 수 있기 때문이다. 이러한 전반적인 pattern을 통해서 서로 similar한지 확인할 수 있다.

물론, 위에서 말한 방법만이 정답은 아니다. 다른 방법을 다른 상황에 적용해도 상관은 없지만 가장 적절한 것을 선택하고자 할 때는 domain의 성질에 따라서 알맞게 선택해주면 된다. Data object의 경우 attribute의 공간에 하나의 point로 존재하게 된다. 이러한 point들 사이의 거리를 구할 때 가장 직관적인 방법은 아마 Euclidean distance일 것이다. 단순하게 2개의 point 사이를 이어주는 직선을 통해서 거리를 구하면 되기 때문이다. 하지만, Mahalanobis distance와 같이 data distribution에 따라서 거리를 측정할 수가 있을 것이다. 우리가 가지고 있는 data의 모양에 따라 결국에는 distance가 바뀔 수가 있다. 더 좋은 distance가 나올 수 있기 때문에 Euclidean distance가 항상 맞는 것은 아니지만 이해하기 가장 직관적인 것은 사실이다. Data의 scale이 다 일정하고 distribution이 상관이 없다면 대부분의 경우 Euclidean distance를 사용할 수 있을 것이다. 예를 들어, 동일한 주제의 신문이 있지만 하나는 한 페이지이고 다른 하나는 두 페이지라고 해보자. 문서들을 단순하게 특정 단어의 빈도수로 비교하게 되면 당연히 두 페이지 문서가 더 많이 나타날 것이다. 이러한 특징을 가진 2개의 data를 비교하기 위해서는 단순하게 Euclidean distance를 사용할 수 없다. Point들로 data를 표현하게 되는데 point들의 위치를 나타내는 vector가 결국 문서가 길어지면 길어질수록 멀리까지 존재하게 될 것이다. 이러한 경우에는 cosine similarity를 사용해서 point들 사이의 거리를 계산하는 것이 아니라, 가리키는 vector의 각도를 사용하면 된다. 이를 semantic information이라고 하고, 이렇게 내포하는 의미를 비교하기 위해서는 cosine을 주로 활용하게 된다. Correlation의 경우는 각 point를 비교하는 것이 아닌 전체적인 trend를 비교하는 것이다. 같이 올라가는지 혹은 내려가는지 아니면 서로 반대가 되는지 등을 고려할 때 사용하면 된다. 그래서 time series와 같은 data에서 correlation이 적절하게 사용되는 것이다.