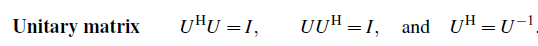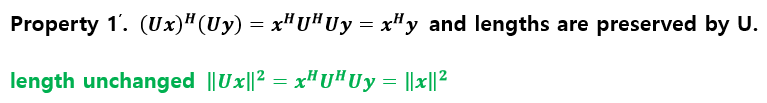행렬 문제 중에서도 가장 기본이 되는 Ax = b를 풀어 해를 찾는 일을 했었다. 이제는 해를 찾을 때 방법이 궁금한 것이 아니고 수의 체계에 대해서 알아볼 것이다. 만약 A와 b가 실수 범위에 해당한다면, x 역시 실수 범위에 해당할 것이다. 그렇다면 복소수는 어떠할 것인가? 복소수도 가능할 것이다. 실수 범위를 넘어 복소수 범위에 대해서 살펴보자.
이전에는 실수 범위 내에서 덧셈과 곱셈 등이 허용되었다. 복소수 범위에서도 덧셈과 행렬 곱셈 등이 허용 된다. 하지만 길이는 계산에 있어서 조금 다르다. 복소수의 경우 제곱을 했을 때 부호가 바뀌는 등의 문제가 있기 때문이다. 그래서 다음과 1의 제곱과 i의 제곱을 했을 때 0이 되는 것은 길이의 측면에서 옳지 않기 때문에 다음과 같이 i는 절대값을 통해서 구할 것이다.
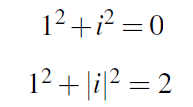이번 내용에서 특히 symmetric matrix와 Hermitian matrix에 초점을 맞춰서 볼 것이다. 그리고 다음 명제들을 보자.
1. Every symmetric matrix (and Hermitian matrix) has real eigenvalues.
2. Its eigenvectors can be chosen to be orthonormal.
위 명제들에 대해서는 우선은 받아들일 내용이고, 차근차근 살펴보도록 하자.
Complex Numbers and Their Conjugates
복소수(Complex number)와 켤레복소수(Conjugate)는 이미 다 알고 있는 내용일 것이다. 중학교 수학 과정 중에 수의 체계에 대해서 기본적으로 다룬 이야기일 것이다. 그래도 간단하게 되짚어 볼 내용들을 살펴보고자 한다.
Lengths and Transposes in the Complex Case
다시 선형 대수의 관점에서 complex number들로 이루어진 벡터 공간이 존재한다고 해보자. 이 공간을 이루는 모든 벡터들은 n개의 complex component를 가질 것이다.
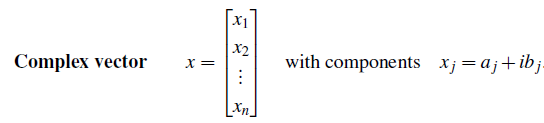그렇다면 2개의 벡터가 주어졌을 때, 이 벡터들의 원소들을 이용하여 덧셈도 가능하게 된다. Complex number를 곱하는 것도 당연히 가능할 것이다. 실수 범위에 해당할 때와 크게 다르지 않다는 것이다. 앞서 말했듯이 길이를 구할 때에는 주의해주면 된다. 우리가 흔히 길이를 구할 때 component들의 제곱의 합으로 구하게 된다. 하지만 complex number의 특성상 길이를 구하고 싶을 때는 절대값을 취한 상태로 제곱의 합을 구하면 된다.
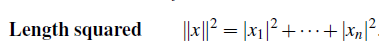예시를 통해서 살펴보자.
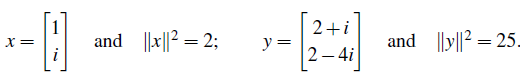위의 벡터의 길이를 구할 때, complex component를 포함하고 있기에 절대값을 취해서 길이를 구해준 것이다.
또한 내적에 있어서도 일종의 변형을 통해서 구해줘야 한다. 그 방법은 다음과 같이 첫번째 내적을 하려는 벡터의 conjugate를 통해서 내적을 구하면 된다.
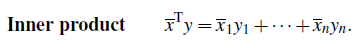원래 real number 범위에서는 그냥 x와 y의 내적을 구하면 됐다. 하지만 complex number 범위에서는 x대신에 x의 conjugate를 해줘야 한다. 사실 이것도 길이의 관점으로 보면 일맥 상통한 것이다.
그래서 complex 범위에서 우리는 하나의 notation을 바꿔줄 것이다. 위에서 conjugate는 문자 위에 바 하나를 통해서 표기해줬다. 그리고 우리는 transpose matrix를 하면 행렬의 위첨자에 T를 적는 것을 알고 있다. 이 2가지를 합쳐서 새로운 notation을 만들고 싶다. 그것이 바로 H이고, 이를 Hermitian이라 부를 것이다.
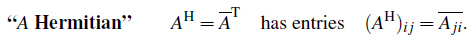간단하게 하나의 complex component를 가지는 행렬에 대해서 hermitian을 살펴보면 다음과 같다.
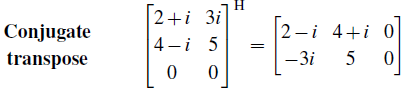그리고 이 conjugate transpose 행렬에 대해서 다음의 성질을 만족할 것이다.
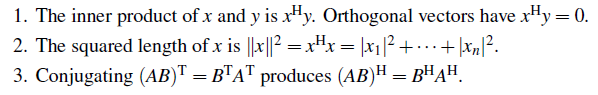
Hermitian Matrices
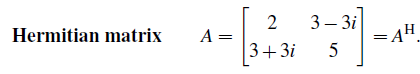Hermitian matrix의 특징은 diagonal entry가 반드시 real number여야 한다. 그리고 diagonal entry를 제외한 off-diagonal entry는 서로 conjugate 관계여야 한다. 즉, complex number에 해당하는 항의 부호가 반대여야 한다. Complex component를 가지면서 symmetric해야 하는데, 여기서 off-diagonal component가 complex conjugate하면 우리는 이를 Hermitian matrix라고 할 것이다.
이제부터 목표는 Hermitian matrix의 기본이 되는 3가지 성질들을 만족시키는 것이다.
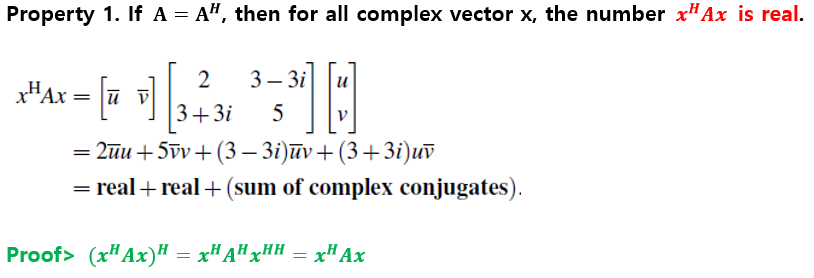
Unitray Matrices
수의 범위를 real에서 complex로 넘어가면서 Hermitian matrix에 대해서 알아보았다. 지금까지 complex component로 이루어진 행렬이 symmetric하는데, off-diagonal component가 complex conjugate인 행렬을 Hermitian matrix라고 알게 되었다.
그리고 행렬 A가 real number로 구성되어 있는데, 모든 column vector들이 서로 직교하고 길이가 1인 경우에 우리는 orthogonal matrix라 불렀다. 여기에 행렬 A가 complex number이면서 column vector들이 서로 직교하고 길이가 1인 경우가 존재할 것이다. 우리는 이러한 행렬을 Unitary Matrix라고 부를 것이다.
