[선형대수] Diagonalization of a Matrix

이전에 행렬 A를 LDU로 분해하는 법도 알아봤으며, QR로 분해하는 법도 알아보았다. 이번에는 eigenvalue와 eigenvector들을 이용해서 $S\Lambda S^{-1}$로 분해할 것이다.
단계별로 진행하자면, $n\times n$ 행렬 A가 eigenvector에 linearly independent하다고 가정해보자. 만약 이 eigenvector들이 S라는 행렬의 column들이라고 한다면 A의 우측에 $S$를 곱하고 좌측에 $S$의 inverse를 곱해주게 되면 우리는 $\Lambda$라는 diagonal 행렬을 얻게 된다. 이 행렬은 대각 원소에 A의 eigenvalue들이 나열되어 있을 것이다.
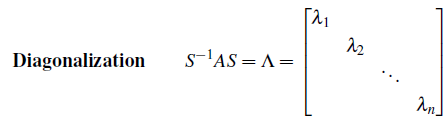우리는 이 $S$를 eigenvector matrix라고 할 것이고 $\Lambda$를 eigenvalue matrix라고 할 것이다.
우리는 Ax = λx로부터 다음과 같은 식들이 성립하다는 것을 알 수 있다.
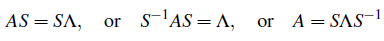여기서 $S$는 invertible해야하는데, 그렇다는 이야기는 $S$는 non-singular해야 한다. 이는 다시 말해서 A의 eigenvector가 linearly independent 하다는 것이다.
우리는 행렬 A에서 eigenvalue와 eigenvector를 matrix form으로 하여금 새로운 분해 방법을 알게 되었다. 그리하여 eigenvector matrix $S$가 A에 곱해짐으로써 A를 eigenvalue matrix Λ로 바꿔주었다.

다음 사실들은 알아둬야하는 몇가지 사실들이다.

1. If eigenvalues of A are different, then eigenvectors of A are linearly independent.

2. The diagonalizing matrix S is not unique. (Eigenvector can be multiplied by a constant and remains an eigenvector)

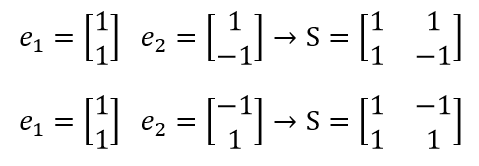
3. The order of eigenvalues is same with that of eigenvecters.

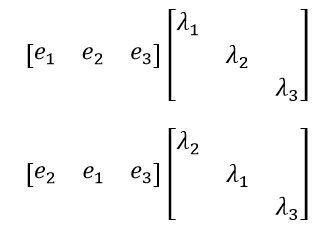
4. Not all matrices have n-linearly independent eigenvectors.So not all matrices are diagonalizale.

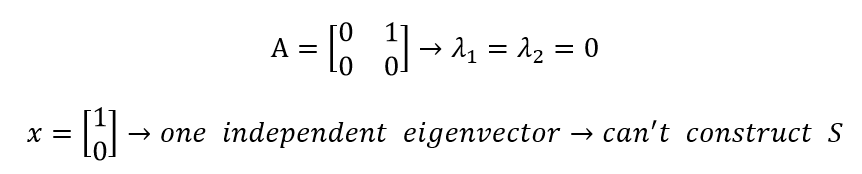
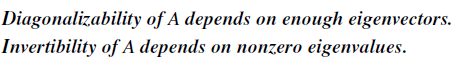Diagonalizability라는 것이 n개의 linearly independent한 eigenvector를 의미하고, Invertibility라는 것이 0이 아닌 eigenvalue를 의미하는데, 이 둘 사이의 어떠한 관계도 없다. 우리가 주목해야하는 것은 diagonalization이 실패한다는 것은 오직 반복되는 eigenvalue가 존재할 때이다. 가령 A = I인 경우에는 전부 1로 반복되는 eigenvalue들이 존재하는데, 이 행렬은 이미 diagonal하다.
정리해보면, A가 n개의 eigenvalue를 가지는 경우에는 반드시 서로 다른 independent한 eigenvector를 가지며 diagonalizable하게 된다. 만약에 A가 어떤 반복되는 eigenvalue를 가지는 경우에는 independent한 eigenvector를 가질 수도 있지만(ex. identity, rotation...), 그렇지 않을 수도 있다(ex. triangular...).

Powers and Products

계산이 쉬워지는 특별한 경우를 알아보고자 한다. 행렬 A를 제곱했을 때의 eigenvalue들은 과연 A의 eigenvalue들을 제곱한 것과 결과가 같을까? Ax = λx에서 시작해서 확인해보자. 여기에 A를 곱하면 다음과 같다.
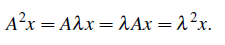식을 잘 변형해서 기존의 식을 대입해보았더니 A를 제곱한 결과 λ도 제곱의 형태가 되었다. 그럼 A의 제곱 상태에서 diagonalization을 시키면 어떻게 될까?
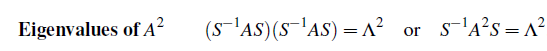A의 제곱도 같은 S에 의해서 diagonalization이 되었으며, eigenvector들도 변하지 않았다. 위의 식은 확장성이 좋은 형태로, 계속해서 제곱수를 늘려갈 수가 있다.

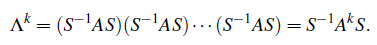
추가적으로, A가 invertible하다면, A의 역행렬의 eigenvalue는 어떻게 될까?
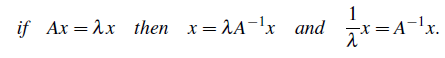Diagonalization 없이 다음과 같이 쉽게 형태 변형만으로도 찾을 수 있다. 즉, eigenvalue의 분자와 분모를 바꿔주면 된다.

마지막으로, A와 B의 eigenvector가 같다면, AB와 BA는 같게 된다. 반대로 AB와 BA가 같다면, A와 B는 같은 eigenvector matrix S를 가지게 된다.