지금까지 Ax = b를 풀고자 이와 관련된 이야기를 했었다. 지금부터는 Ax = λx를 풀어보는데 집중할 것이다. 가능하다면 행렬을 diagonal로 만들어 쉽게 푸는 방법에 대해서 알아볼 것이다. 그리고 Ax = b에서는 elimination을 통해서 더 쉽게 풀고자 했지만, Ax = λx에서는 elimination을 진행하지 않을 것이다. Row exchange를 통해서 elimination을 하게 되면 eigenvalue의 결과가 달라지게 된다. 여기서 eigenvalue가 무엇인지 간단하게 정의를 살펴보면, 선형대수학에서 선형 변환의 고유 벡터(Eigenvector)는 그 선형 변환이 일어난 후에도 방향이 변하지 않는, 영벡터가 아닌 벡터이다. 고유 벡터의 길이가 변하는 배수를 선형 변환의 그 고유 벡터에 대응하는 고윳값(Eigenvalue)이라고 한다. 선형 변환은 대개 고유 벡터와 그 고윳값만으로 완전히 설명할 수 있다. 위의식 Ax = λx에서 λ가 eigenvalue에 해당하고, λ와 곱해진 x가eigenvector에 해당하게 된다.
가장 먼저 이해할 내용으로는 어떻게 eigenvalue가 유용한지이다. 미분 방정식에서 흔히 eigenvalue가 사용된다. 복잡한 미분이 아니라 고등학교 정도의 간단한 미분 정도만 알고 있어도 된다. 우리는 eigenvalue가 왜 유용한지에 대해서 알아볼 것이기 때문이다. 다음의 예제를 보자.
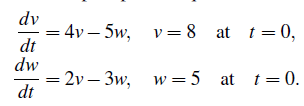우리는 이것을 initial-value problem이라 하고, 여기서 시간 t = 0일때의 미지수는 초기값 8과 5에 의해서 정해진다. 우리가 찾고싶은건 이후 시간 t > 0일때의 v(t)와 w(t)이다. 이 식을 우리는 간단하게 matrix form으로 표현할 수 있고, 우리가 궁금해하는 미지수 벡터를 u(t)라고 하고, 이때의 초기값을 u(0)라고 할 것이다. 그리고 계수를 이용하여 행렬 A를 만들 것이다.
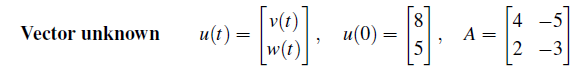2개의 방정식이 우리가 원하는 벡터 방정식이 되었다.
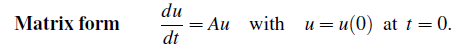이 식에 대해서 알아보면, 이것은 한번의 미분을 뜻하기에 first-order equation이고 더 높은 차원의 미분은 없다. 그래서 이것은 미지수에 대해서 linear하고, 또한 constant한 coefficient를 가지고 있기에 A는 시간에 independent하다.
우리는 어떻게 u(t)를 찾을 수 있을까? 만약에 2개가 아닌 하나의 미지수만 존재한다면 쉽게 찾을 수 있을 것이다. 하지만 우리는 2개를 찾아야 한다. 이를 위해서 다음과 같이 single equation을 풀고자 한다. 이는 vector equation 대신에 scalar를 가지고 있다.
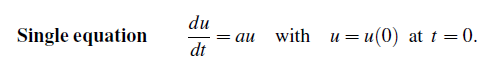이 방정식에 대해서 해를 구하고자 할 때, 다음의 식을 이용하게 될 것이다.
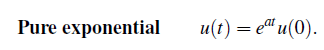초기 시간 t = 0일 때, u는 u(0)와 같게 된다. 그리고 v(t)와 w(t)는 다음과 같이 적을 것이고, 혹은 vector 방식으로 u(t)를 적을 것이다.
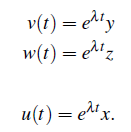이제 여기에 원래의 식을 대입할 것이다.
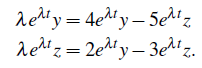그리고 공통 계수를 지우고 남은 식을 통해서 다음과 같이 만들 것이다.
이 식들이 eigenvalue equation이고, matrix form으로는 Ax = λx가 된다.
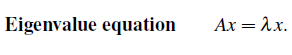위의 미분 방정식을 몰라도 선형대수 측면에서는 크게 상관이 없다. 우리가 구하고 싶은건 eigenvalue와 eigenvector이고, 우리의 목표는 이것들을 찾아서 활용하는 것에 있다.
The solution Ax = λx
Eigenvalue와 eigenvector를 찾는 것이 목표고, 이를 나중에는 활용할 것이다. Ax = λx는 linear하지 않음을 알 수 있다. x와 λ가 곱해져 있기 때문인데, 여기서 λ를 찾게 된다면, 이 식은 x에 대해서 linear해질 것이다. 이 식을 풀기 위해서 λx를 λIx로 바꿔서 해를 구할 것인데, identity matrix를 곱해도 결과가 바뀌지 않는다. 그리고 이를 등호 기준 한쪽으로 모으면 다음과 같다.
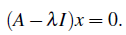이 식을 풀기 위해서 다음 2가지 정보가 핵심이 될 것이다.
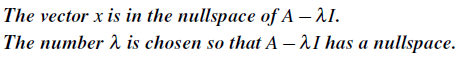모든 행렬이 nullspace를 가지게 될텐데, 이때 벡터 x가 0이면 위의 식을 항상 만족은 하는데 쓸모가 없을 것이다. 그래서 우리는 nonzero x를 원하기 때문에 N(A-λI)는 반드시 0이 아닌 벡터를 가지고 있어야하는데, 그러기 위해서는 A-λI가 반드시 singular해야 한다. 그래서 우리는 det(A-λI) = 0을 이용해서 eigenvector와 eigenvalue를 구해볼 것이다.
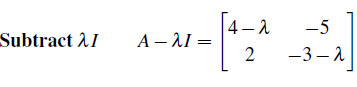
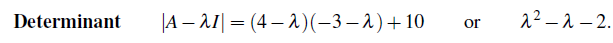위의 식을 풀게 되면, λ는 (-1)이나 2가 나오게 된다. 이 두가지 경우를 다 살펴봐야 한다.
Examples of particularaly good matrices
1. Diagnoal matrix
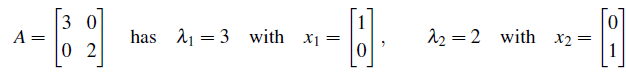행렬 A가 diagonal이면 모든것이 깔끔해진다. 우선 각각의 대각 원소가 eigenvalue가 되고, 이에 대응하는 eigenvector는 unit vector가 된다.
2. Projectrion matrix
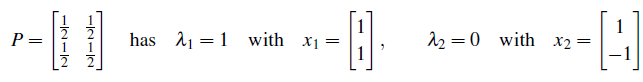행렬 A가 projection matrix이면 eigenvalues는 1 아니면 0이 된다. 1이면 벡터 x는 자기 자신에 project할 것이고, 0이면 x는 0 벡터에 project할 것이다.
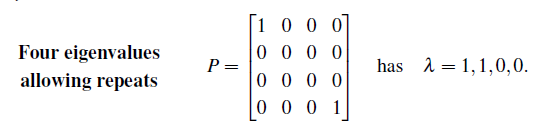
3. Triangular matrix
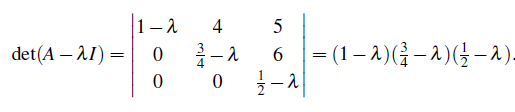행렬 A가 triangular matrix이면 diagonal과 마찬가지로 eigenvalue는 대각 원소가 된다.
