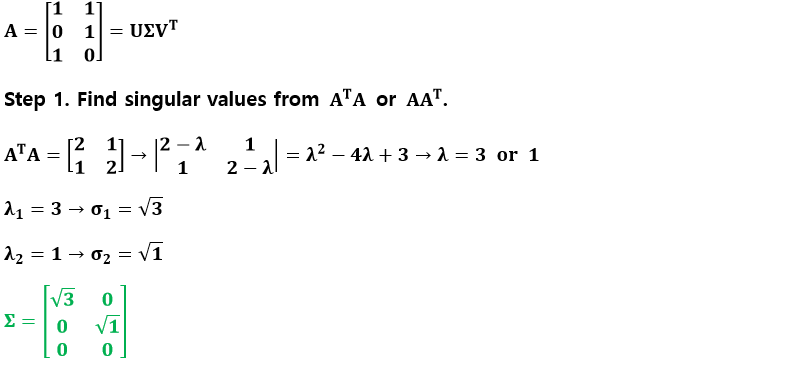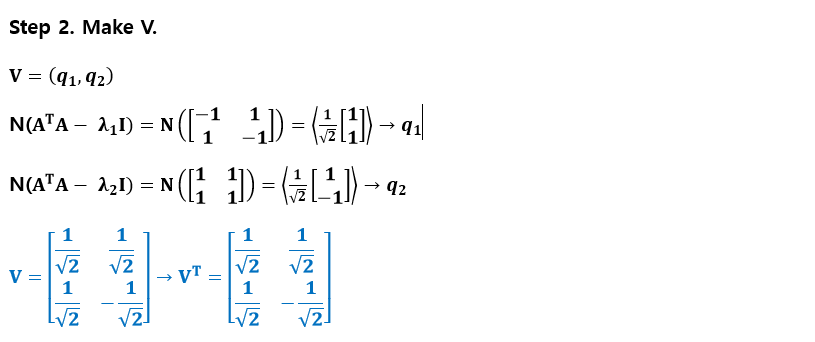[선형대수] Singular Value Decomposition(SVD)

행렬 A가 주어졌을 때, 여러 matrix factorization을 알고 있다. 아마 활용하는 측면에서 이번에 하는 특이값 분해(Singular Value Decomposition)이 가장 좋다고 생각한다.

Singular Value Decomposition(SVD)

SVD는 eigenvalue decomposition과 같이 행렬을 대각화하는 일종의 방법이다. SVD가 그럼에도 더 나은 점을 이야기하자면, 정방 행렬이 아닌 어떠한 $m \times n$ 크기의 행렬에 대해서 적용이 가능하다. 먼저 행렬 A를 SVD을 진행한다고 했을 때, 다음과 같이 정의할 것이다.
A와 A의 transpose를 곱하거나 이를 순서를 바꿔서 곱하게 되었을 때는 항상 symmetric matrix가 나오게 된다. 여기서 흥미로운 사실로는 이들의 곱을 통한 eigenvalue가 모두 0 이상이며, 만약 0이 아닌 eigenvalue가 존재할 때에는 서로 동일하다는 점이다. Eigenvalue들이 0 이상이 되어야 square root를 계산할 수 있어 diagonal matrix의 component로 하여 행렬을 분해할 수 있다. 그렇다면 이제 SVD를 통해서 알게되는 점들에 대해서 정리해보자.
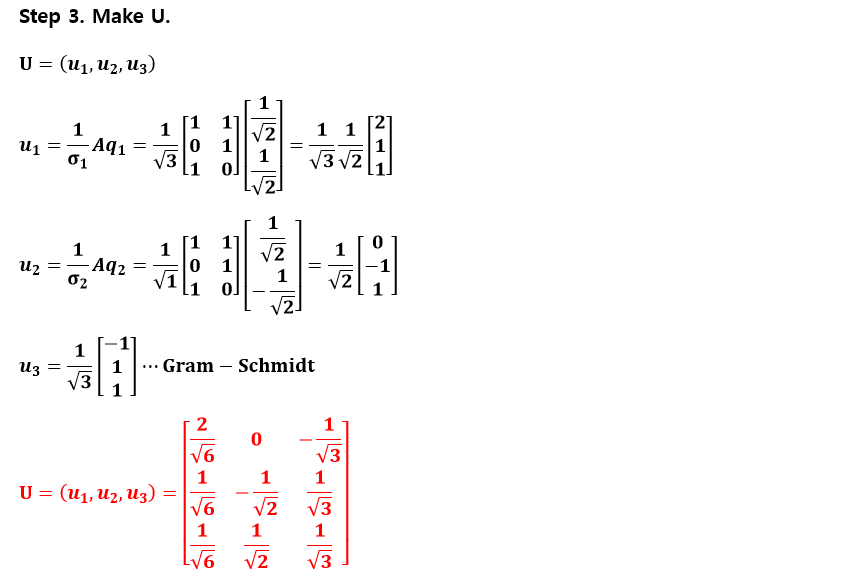
어떠한 크기의 행렬이 주어지든 상관없이 우리는 SVD를 진행할 수 있다. 다음의 예시를 한번 보자.