Eigenvalue를 구하는 방법에 대해서는 알게 되었다. 그러나 eigenvalue의 부호에 대해서 생각해 본 적이 있는가? 그저 계산 방법에 의해서 eigenvalue를 구했고, 이 값이 양수인지 음수인지에 대해서는 크게 신경쓰질 않았다. 우리는 어떤 test를 통해서 행렬 A가 주어졌을 때, eigenvalue를 직접 구하지 않고 오로지 test를 통해서 eigenvalue의 부호가 양수가 보장되는지를 알아보고자 한다.
이전에는 몰랐지만 앞으로 eigenvalue의 부호는 굉장히 중요해진다. 우리는 여기서 positive definite라는 내용을 다루게 될텐데, 이는 후에 행렬식의 관점에서 symmetric matrix의 특수한 경우로 아주 유용하게 사용이 되는 내용이다. 이전에 모든 symmetric matrix는 real eigenvalue를 가진다고 했다. Positive definite matrix도 마찬가지로 real eigenvalue를 가지지만, 특별하게 모두 양수인 경우를 말한다. 우선 정의를 살펴보기 위해서 고등학생 때 배운 2차 함수를 가지고 이야기할 것이다. 다음의 2가지 예제 F(x, y)와 f(x, y)가 있다고 하자.
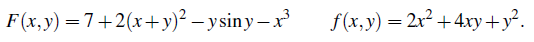위의 두 식에서 x = y = 0 지점에서 최소값을 가지는가?
우리는 어떠한 지점에서 최소값을 가지는지, 혹은 최대값을 가지는지, 아니면 의미 없는 값을 가지게 되는지 궁금한 것이다.
원하는 지점이 (0, 0)이기에 이 값을 우선 대입해보자. 그러면 F(0, 0) = 7, f(0, 0) = 0이 될텐데, 이 값을 통해서는 해당 식에 대해서 최소값인지 최대값인지 아니면 그 중간값인지 도무지 알 수가 없다. 고등학교를 다니면서 함수 식을 해석하는 방법을 배운 적이 있다. 식을 미분하게 되면 어느정도 함수 식이 나타내는 형태를 이해할 수가 있다. 그래서 우리는 각각의 식이 다변수 함수이기 때문에 각각 x와 y에 대해서 1차 미분을 해볼 것이다.
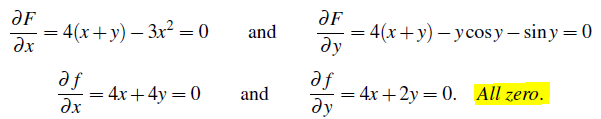이렇게 미분을 통해서 F와 f 모두 (0, 0)이 stationary point라는 것을 알았다. 기울기의 변화 지점이라는 의미이다. 즉, 이 부분이 어떠한 의미를 가지는 지점이라는 것이다.
그래서 우리는 위의 식을 x와 y에 대해서 2차 미분을 해볼 것이다.
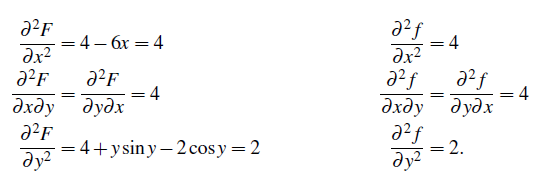F와 f 모두 (0, 0)에서 4, 4, 2라는 공통된 결과가 나왔다. 이 이야기는 두 함수 모두 원점 근처에서 정확하게 같은 행동을 취한다는 것이다. 즉, F가 minimum을 가지는 것은 f도 minimum을 가지는 것이다. 함수가 (0, 0)을 제외한 모든 지점에서 모두 0보다 큰 값을 가지면 우리는 이를 positive definite라고 할 것이며, 이는 후에 자세히 다룰 것이다. 우선 의미적으로만 알고가보자.
다시 돌아와서, 함수를 2번 미분한다는 것이 원래는 4가지 결과를 가지게 되는데 x와 y를 한번씩 진행하는 2차 미분은 결과 같기 때문에 3가지 결과를 가지고 F와 f가 minimum을 가지는지 아닌지 확인할 것이다.
이변수 함수에서 positive definite, negative definite, saddle의 판단 방법을 알아보았다. (0, 0)을 기준으로 전부 양수인지 음수인지는 함수 식의 계수들의 관계를 통해서 간단하게 판단할 수 있다. Saddlle point는 방향에 따라 극소점과 극대점이 모두 가능하기에 붙여진 이름이다.
